高超聲速飛行器快速平滑自適應二階滑模控制
文成馀,江 駒,余朝軍,朱 平
(先進飛行器導航、控制與健康管理工業和信息化部重點實驗室(南京航空航天大學),南京 210016)
高超聲速飛行器突防、偵察能力強,反應時間短,飛行速度快,在軍事和民用領域有著眾多需求[1-2].但是由于其具有嚴重非線性、強耦合性、不確定性等特性,這給飛控系統的設計增加了難度,特別是在爬升段,飛行器要穿越對流層、平流層、中間層以及部分電離層,飛行速度從超聲速加速到高超聲速,不確定性因素[3]更多.
超螺旋滑模控制算法[4]因其具有強魯棒性且只需要知道滑模量的信息,無需知道其一階導數的信息等特性,已廣泛應用于干擾估計[5]、極值搜索控制[6]、容錯控制[7]等相關領域.文獻[8]提出了一種快速超螺旋算法,通過在普通超螺旋算法中加入線性項,提高了算法的收斂速度,并基于此算法設計干擾觀測器對干擾連續估計和補償.文獻[9]同樣通過加入線性項來提升收斂速度,并在假設干擾上界未知的前提下,設計了一種新的自適應律,提出一種新型的快速自適應超螺旋算法.文獻[10-12]通過設計一種自適應參數既可增大又可減小的自適應律,以解決參數過大估計問題.上述這些算法由于積分項中含有不連續的符號函數項,只可得到連續的控制輸入曲線,控制輸入不平滑,與傳統一階滑模相比,這些控制算法的確減小了抖振,但是并不能極大減小甚至消除抖振.2007年文獻[13]提出一種平滑的二階滑模控制算法,其主要思想就是在超螺旋算法的積分項中使用連續的函數,以此得到平滑的控制輸入,但是這種控制方法需要非線性觀測器來估計干擾,而且算法的收斂速度上還有提升的空間.
本文針對上述所存在的問題,提出一類新型的快速平滑自適應超螺旋滑模控制算法.采用滑模微分器逼近反饋線性化過程中不準確的量;控制律設計時,在普通超螺旋算法中增加線性項,并在積分項中使用連續的函數,以加快收斂速度且達到平滑控制的效果;最后,為避免參數過大估計,設計了一種自適應參數可增可減的自適應律.
1 問題描述
1.1 動力學模型
高超聲速飛行器爬升段縱向動力學模型可以描述為:
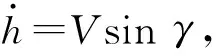
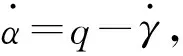
(1)
式中:M為飛行器質量;V為飛行速度;γ為航跡傾斜角;h為飛行高度;α為飛行迎角;q為俯仰角速率;Iyy為縱向轉動慣量;r=R+h為飛行器地心距,其中R為地球半徑;μ0=3.986×1014m3/s2為地球重力常數;g0為地表重力加速度;Isp為燃料比沖;L、D分別為飛行器升力、阻力;T為發動機推力;My為俯仰力矩;dv1、dγ、dq分別為模型不確定性、外部干擾等復合干擾.
1.2 發動機推力模型
高超聲速飛行器的推力模型可簡化為一個二階模型:
式中:βc為發動機節流閥的調定值;阻尼比ζ為0.7;固有頻率ωn為5.
推力系數以及燃料比沖公式為:
式中:CT為推力系數,Ma為馬赫數.
1.3 空氣動力與動力矩
高超聲速飛行器的氣動力與氣動力矩可表示為:
式中:Sw為機翼浸潤面積;cA為平均氣動弦長;ρ為空氣密度;CT、CL、CD、CMy分別為推力、升力、阻力以及俯仰力矩系數,其均與α、Ma相關,具體值詳見文獻[14].
1.4 控制問題
1)由于高超聲速飛行器本身缺乏飛行試驗數據等[15]問題,加上爬升的過程中,飛行速度、高度急劇增加,燃料大量消耗導致重心較寬范圍變化等因素,將會造成模型、參數等不確定性.本文主要研究高超聲速飛行器在爬升的過程中參數Sw,cA,Iy,ρ,CD,CM,CL存在攝動,且存在除參數不確定外的復合干擾時的軌跡控制問題.
2)抖振普遍存在于滑模控制中,如何削弱抖振,將其抑制到極小范圍內甚至消除,一直是控制領域的熱點問題.二階超螺旋滑模將符號函數放到積分里,有效地抑制了抖振,但是并沒有消除抖振.假設某系統有如下控制算法:
(2)
式中:u為控制輸入;e為跟蹤誤差;k1、k2為控制參數.由式(2)可知,雖然符號函數通過積分,使得控制輸入連續,但是不平滑,當e在0附近變化時,控制輸入曲線會呈鋸齒狀.本文控制算法旨在既能將控制輸入平滑化,又能提升收斂速度.
2 精確反饋線性化
2.1 輸入/輸出反饋線性化
定義向量x=[V,γ,α,β,h,M]T,將V、h分別對時間求三次和四次微分,微分表達式中將出現控制輸入量,將其作為整體提取出來,可得:
(3)
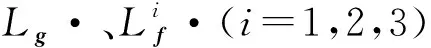
2.2 滑模微分器
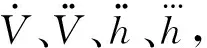
滑模微分器設計為

引理1[4,16]設f(t)=f0(t)是定義在[0,]上的函數,且有|f(n+1)|≤Sn,?t,其中Sn為已知正常數.則在經歷有限時間的瞬態過程后,有
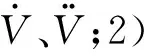
根據引理1,選擇合適的參數,可以保證滑模微分器的狀態量在有限時間內精確跟蹤速度和高度的各階導數.
3 快速平滑自適應二階滑模算法
3.1 積分滑模面
定義速度和高度的跟蹤誤差:
eV=V-Vd,eh=h-hd,
(4)
式中Vd、hd為指令信號.
為了保證穩態跟蹤精度,選擇積分滑模面.根據式(3),系統的相對階次分別為3和4,所以設計滑模面如下:
(5)
式中λV、λh為待設計參數.
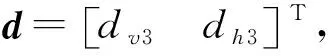
3.2 控制器結構
快速平滑自適應二階滑模控制系統結構框圖如圖1所示.
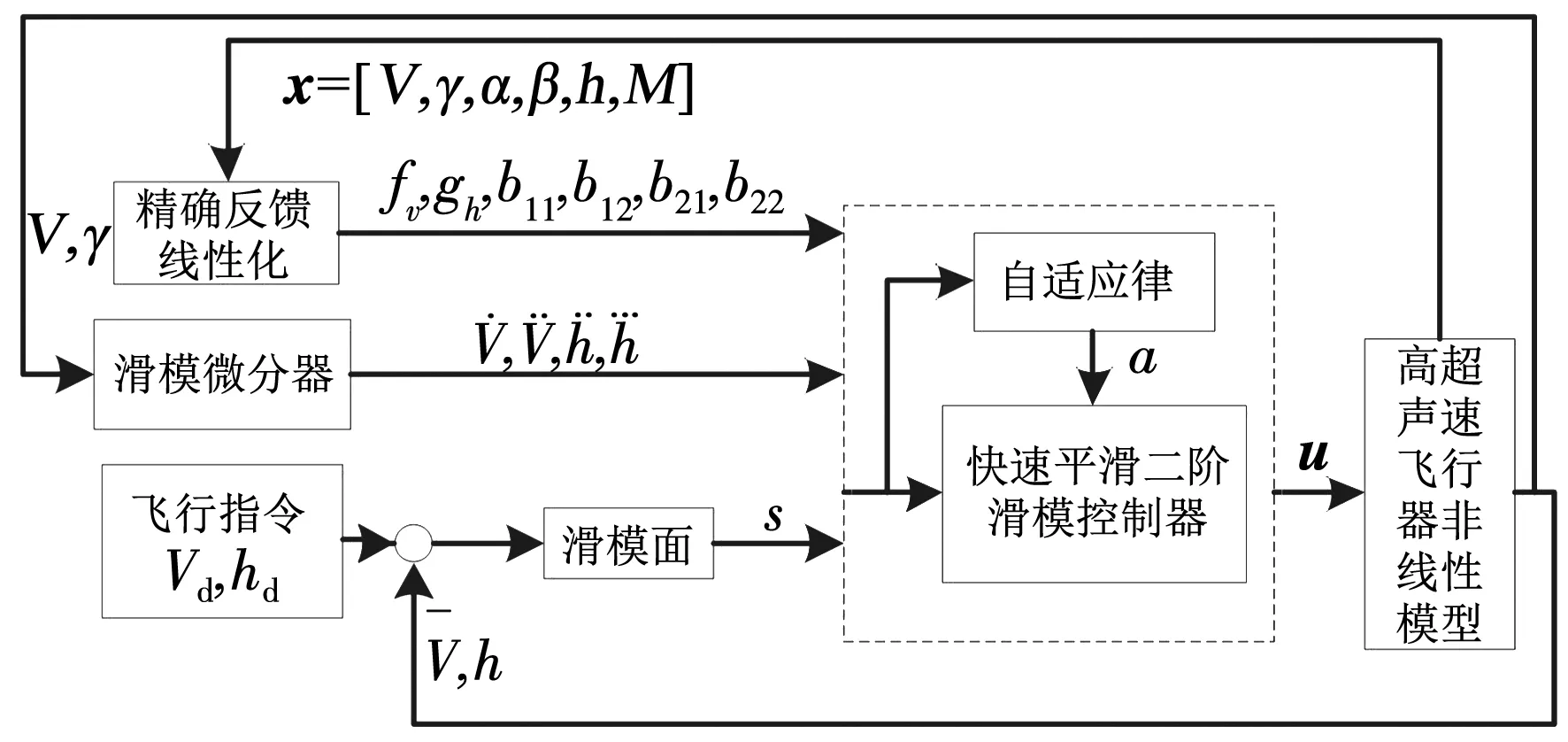
圖1 總體控制結構框圖
在圖1中,快速平滑二階滑模控制律可設計為:
(6)

(7)
式中:自適應律設計參數ω1,γ1>0,μ=[μ1μ2],μ1、μ2為較小的正常數.
根據式(3)、式(4)~(6)可計算得出閉環滑模面趨近動態.鑒于滑模面sV和sh的趨近動態形式相同,下文省去下標為s,其中aVi、bVi、ahi、bhi(i=1,2),dv3,dh3同理,可得:
(8)
情況1當m=2時,對比式(2),該算法加入了線性項a1b2s、a2b2s,可保證|s|快速收斂到μ鄰域內,但是該算法并不平滑.
情況2當m>2時,不僅可保證快速收斂,且控制輸入式(6)的積分項中均是連續的函數項,故此時的控制輸入是平滑的.
3.3 收斂性證明
定理1對于包含被控系統(1)、控制律(6)、自適應律(7)的閉環系統,若假設1滿足,則s在有限時間內收斂于μ鄰域內.
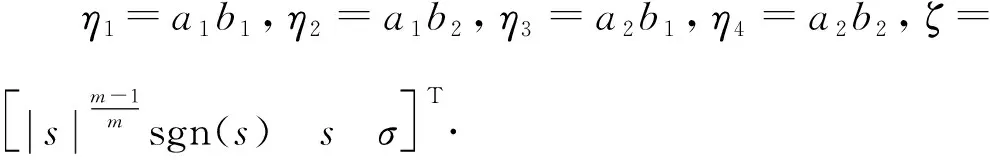
定義類二次型Lyapunov函數為
(9)
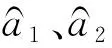
對V求一階導:
(10)
式中:
C=[-η1-η22].
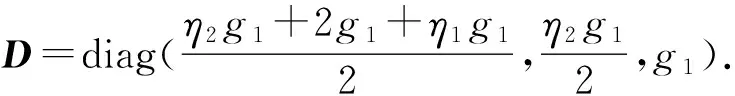
則式(10)可為
(11)
令A和B-D均為正定矩陣,可解算得:
(12)
根據:
λmin(Q)‖ζ‖2≤ζTQζ≤λmax(Q)‖ζ‖2,
(13)
(14)
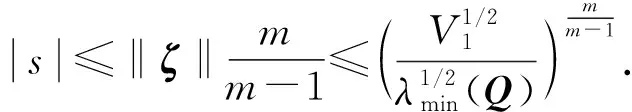
(15)
式中:
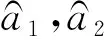
(16)
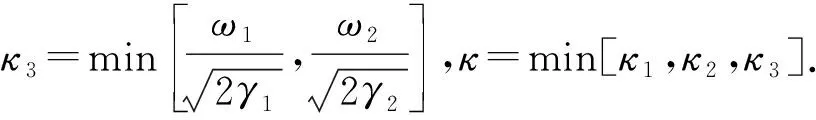
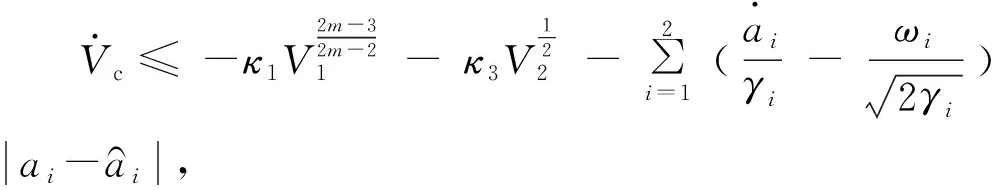

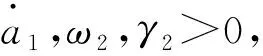
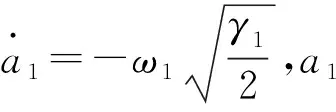
因此,在自適應過程中,|s|可能在有限的時間(t3-t1)內離開μ鄰域,并保證其始終停留于一個更大的鄰域μ1,即|s|≤μ1,下面估計μ1鄰域的界.
根據式(9)和式(11),有
再根據不等式(13),可將上述不等式化為
(17)
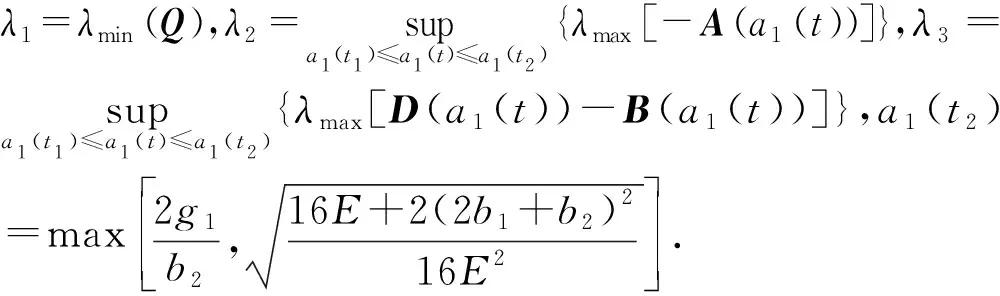
在|s(t1)|=μ的初始條件下,求解微分不等式(17),可得到:
‖ζ(t)‖≤
上式可得到t2時刻‖ζ‖的最大值,為了估計此時|s|的最大值,令等式(14)中σ=0,可獲得|s(t2)|的最大估計值μ1=|s(‖ζ(t2)‖)|.
定理1得證.
4 數值仿真
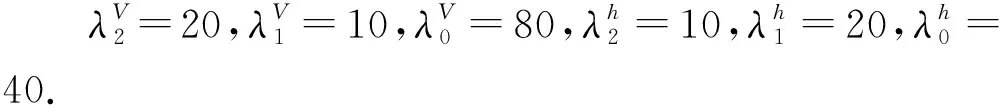
4.1 仿真1
為驗證滑模微分器對反饋線性化過程中非匹配不確定性的抑制作用,進行仿真1. 仿真結果如圖3所示.
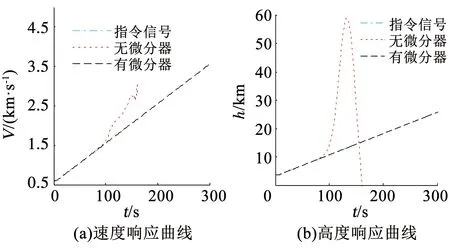
圖3 仿真1結果
為體現非匹配不確定性的影響效果,本文加入較大的不確定性及干擾,從仿真結果圖3可以看出,使用滑模微分器估計速度和高度各階導數的控制器,高度和速度輸出信號均能準確地跟蹤上指令信號,而未使用滑模微分器的控制器在接近100 s時已經發散,可知在存在較大不確定性及干擾的情況下,忽略反饋線性化過程中的非匹配不確定性,是不合理的,設計出的控制器可能無法達到預期控制效果.
4.2 仿真2
為驗證本文控制算法既快速又平滑的特性,進行仿真2,選擇3種控制器:1)選取m=4的快速且平滑的超螺旋滑模控制(FSSTC)器;2)選取m=2的快速但不平滑的超螺旋滑模控制(FNSSTC)器;3)傳統超螺旋滑模控制(STC)器.仿真結果如圖4所示.
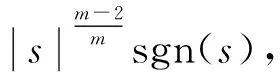
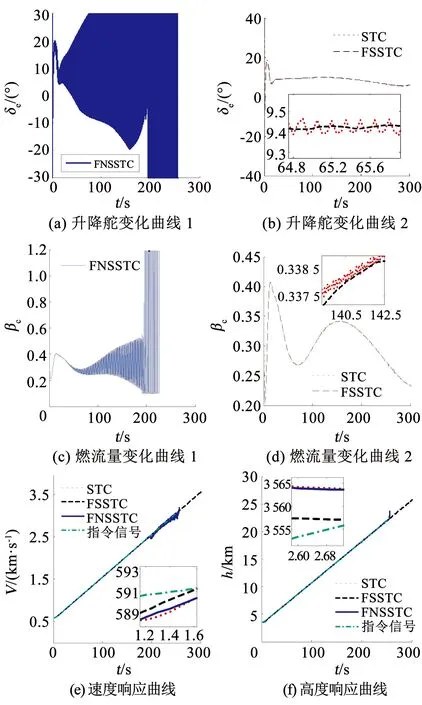
圖4 仿真2結果
注本文的控制算法中引入了線性項,原理上收斂速度較傳統二階滑模控制算法要快,但是設計自適應律可能減小其收斂速度,又由于本文設計的自適應律,其參數既可增大又可減小,不會造成參數過大估計,即可選取較大的初始值,保持更快收斂速度.
5 結 論
1)本文針對高超聲速飛行器爬升段的控制問題,提出了一種快速平滑的自適應二階滑模控制算法.
2)鑒于反饋線性化過程中存在的非匹配不確定性,采用了滑模微分器來逼近反饋線性化模型中速度和高度的各階導數,同時為改善傳統超螺旋控制算法的收斂速度以及控制輸入平滑性,在其算法中加入了線性項,并將積分項中的符號函數項進行了連續化.
3)仿真結果表明,加入滑模微分器后,成功消除了非匹配不確定性的影響,且該方法有較好的跟蹤性能,與傳統STC算法和FNSSTC算法相比,有更快的收斂速度,且控制輸入平滑,基本消除了抖振.
4)實際應用中,控制輸入多為機械運動,意味著控制輸入越平滑,則具有更好的工程實用價值.

