人船模型解題研究

◇ 湖北 戈 菲

(作者單位:湖北省宜昌市葛洲壩中學)

人船模型問題不僅僅是動量守恒問題,更是力學綜合問題,此類問題涉及動量、能量、力與運動等知識,解題方法有規(guī)律可循.本文通過對例題的分析,總結人船模型的解題方法,希望對師生有所幫助.

1 例題及解析

例1如圖1所示,質量為M 的物體靜止于光滑水平面上,其上有一個半徑為R 的光滑半圓形軌道,現(xiàn)把質量為m 的小球自軌道左側最高點由靜止釋放,問:(1)擺球運動到最低點時,小球與軌道的速度是多少? (2)軌道的振幅是多大?

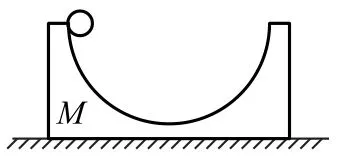
圖1

(1)設小球到達最低點時,小球與軌道的速度分別為v1和v2,根據(jù)系統(tǒng)在水平方向動量守恒,得mv1＝Mv2,又由系統(tǒng)機械能守恒得

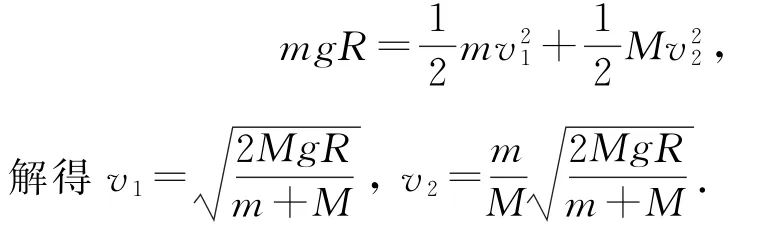
(2)當小球滑到右側最高點時,軌道左移的距離最大,即振幅A.由人船模型得mx＝My,x＋y＝2R,解得即振幅

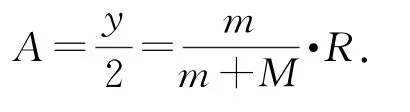
例2(2018年新課標卷Ⅰ)質量為m 的煙花彈獲得動能E 后,從地面豎直升空.當煙花彈上升的速度為零時,彈中火藥爆炸將煙花彈炸為質量相等的兩部分,兩部分獲得的動能之和也為E,且均沿豎直方向運動,爆炸時間極短,重力加速度大小為g,不計空氣阻力和火藥的質量.求:(1)煙花彈從地面開始上升到彈中火藥爆炸所經(jīng)過的時間;(2)爆炸后煙花彈向上運動的部分距地面的最大高度.

(1)設煙花彈在地面時的速度為v0,則E＝煙花彈豎直上拋,則聯(lián)立可得

(2)設煙花彈上升高度為h1后爆炸,根據(jù)機械能守恒定律可得E＝mgh1.爆炸后兩者質量均為豎直方向根據(jù)動量守恒定律可得,二者的速度相等,均為v,二者的動能均為設向上運動的部分繼續(xù)上升的高度為h2,根據(jù)能量守恒定律得聯(lián)立以上各式可得

2 解題方法總結

動量守恒定律是高考的必考內容,而人船模型是動量守恒定律的重要題型之一.認識模型、舉一反三、善于遷移與變通對于試題的解決有很大的幫助.本文總結解題方法如下:

1)掌握人船模型的3個條件:a)多個物體組成的系統(tǒng)初狀態(tài)靜止;b)多個部分相對運動過程中,系統(tǒng)所受合外力為零或者某一方向上合力為零;c)多個部分對地位移之和為定值.滿足以上3個條件的問題,可以視為人船模型問題.

2)掌握解決問題的必要物理知識,加強對物理概念、物理規(guī)律的認識和理解.例如學習動量守恒定律,一要知道動量守恒定律如何而來;二要知道動量守恒定律的內容、公式;三要知道公式成立的條件,即合外力為零,或者合外力遠小于內力;四要知道公式的性質,例如動量守恒定律的矢量性、瞬時性等.

3)掌握人船模型的核心內容及涵蓋范圍.人船模型以動量守恒定律為核心考點,以運動、受力、能量為覆蓋點,構成“一核三翼”的力學綜合問題.

4)掌握人船模型的常見變式.人船模型的起源是人在船上從一端走到另外一端,這是常見的問題.其變式還有:a)豎直方向上的人船模型(例2);b)曲線運動中的人船模型(例1);c)多物體的人船模型.掌握原型并將規(guī)律靈活應用于變式之中,可以提高解決問題的速度和準確率.

總之,人船模型是動量守恒問題中的一種常見模型,與子彈打木塊模型、反沖模型、彈簧—物塊模型等的解題方法有相似之處,但也有不同之處.我們要做好知識儲備,了解人船模型的應用條件、掌握人船模型的核心考查點,靈活處理變式問題,從而突破此類問題的學習難點.