高中數學解題的基本方法
———以函數與方程為例

◇ 山東 梁桂媛 李愛霞

(作者單位:山東省青州第一中學)

在解題過程中,數學思想和基本方法是解題的關鍵之處和靈魂所在.掌握好數學思想,解題就能如魚得水,從而達到事半功倍的效果.所以高中數學教師在講解新課的時候要注重對數學思想和數學解題方法的滲透,在上習題課的時候注重對數學解題方法的總結,從而幫助學生建立數學解題基本方法的框架,在解題時有規律性和條理性,提高解題的正確性.

1 配方法

配方法的主要思想是對題目中給出的關系式進行變形,得到已知條件和未知條件之間的數量關系.在使用完全平方式的時候需要注意,如果題目的已知條件或未知條件中含有一元二次函數、一元二次方程或是一元二次不等式,可以依據完全平方公式通過加項或減項的方式進行變形,最后得到完全平方的形式,達到“化繁為簡”的目的.

例1若方程x2＋y2－4kx－2y＋5k＝0 表示圓,則k 的取值范圍是多少?

將圓的一般方程x2＋y2－4kx－2y＋5k＝0化為圓的標準方程

該方程表示圓,需要滿足4k2－5k＋1＞0,從而可以通過因式分解進行求解,將4k2－5k＋1＞0化為

2 換元法

在解題的過程中,換元法也是我們經常應用的一種方法,換元法的主要思想是在一道數學題目中,把某個式子看作一個整體,在解題過程中,用一個簡單的變量代替一個復雜的式子,達到“化繁為簡”的目的.在換元的過程中,我們應該遵循的原則為“化繁為簡”,盡量將一般式化為標準式.在解題的過程中,需要特別注意的一點是進行換元后,要注意新元的取值范圍.

例2設實數x 和y 滿足x2＋2xy－1＝0,則x＋y 的取值范圍為________.

x2＋2xy－1＝0可化為－x2＋2x2＋2xy－1＝0,即x2－2x2－2xy＋1＝0,故可以得到x2－2(x＋y)x＋1＝0.

將x＋y＝k 代入上式,可以得到x2－2kx＋1＝0,此時等量關系式變為含有未知量x 的一元二次方程,若方程有解,則需要滿足Δ＝b2－4ac≥0,即

解得k≤－1或k≥1.

3 待定系數法

在有些數學題目中,我們需要確定自變量和因變量之間的函數關系,此時需要預先設出自變量,然后根據題目中的條件,列出含有未知系數的關系式,最后根據題目中給出的已知條件,列出關于待定系數的等量關系式,再求解待定的系數.

例3已知直線l的表達式為2x＋3y＋5＝0,假設存在一條直線m 與直線l 平行,并且直線m 過點(1,－4),求直線m 的表達式.

因為直線m 與直線l平行,所以可設直線m的表達式為2x＋3y＋c＝0,又因為直線m過點(1,－4),則將點(1,－4)代入2x＋3y＋c＝0中,得2×1＋3×(－4)＋c＝0,解得c＝10,即求得直線m 的表達式為2x＋3y＋10＝0.

4 定義法

定義法也是我們在解題的過程中常常應用的一種方法,在講解新知識的時候,教師都會從定義開始講起,只有把握好定義,才能為后面的學習奠定良好的基礎,所以定義是解決問題的根本,利用定義進行解題,就是我們常常說的定義法解題.

例4證明:函數f(x)＝－x3＋1 在(－∞,＋∞)上是減函數.

證明設?x1,x2∈R且x1＜x2,可知

因為x1＜x2,得到x2－x1＞0,且在x1與x2中至少有一個不為0,不妨設x2≠0,故

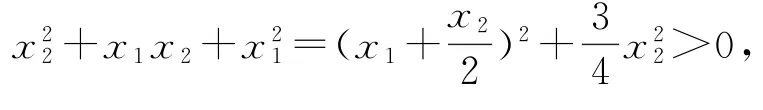
所以f(x1)＞f(x2),故f(x)在 (－∞,＋∞)上為減函數.