掌握基本定義,從根源解決函數問題

◇ 云南 李光和

(作者單位:云南省紅河州金平縣第一中學)

任何函數都有定義的法則,這是判斷函數性質最基本的方法,也是解決問題較為有效的手段.隨著各類函數問題在考查方式上的深入,學習的知識點越來越復雜、越來越多元,學生往往會忽略最基本的定義問題,包括函數的基本形式或某一函數具體性質的證明等.加強學生對定義的掌握,能夠更好地幫助學生去理解函數及其性質的核心要義,從基礎出發,才能穩扎穩打,進而解決更深層次的問題.

1 函數形式的定義

我們學習過很多種函數,如冪函數、指數函數、對數函數等,這些函數都有其獨特的定義和性質.這類知識點是較為基礎的知識點,同時也是學生最容易忽視的知識點.牢牢記住函數的基本定義,能在很大程度上幫助學生理解題目,從而順利求解問題.

例1冪函數f(x)的圖象過點那么f(8)的值為________.

設冪函數的解析式為f(x)＝xα,因為冪函數f(x)的圖象過點所以解得所以

本題主要考查用待定系數法求函數的解析式,再求函數的值.為了加強學生對函數定義的學習,很多題目會直接從定義入手給出條件,再引出問題.此題題干給出函數f(x)是冪函數,需要學生聯想到冪函數的定義,即f(x)＝xα,然后在此基礎上列方程,解方程,最后將未知數代入求解函數值.這類題目需要學生牢牢掌握函數基本定義與具體形式,加強對基礎的訓練,形成慣性思維,才能在第一時間快速高效地解題.

2 函數性質的定義

函數形式多種多樣,性質也廣泛多元,包括單調性、奇偶性等諸多性質,這些性質如同函數一樣,有其基本的定義方法和適用要求.如今對單一的函數性質、定義考查已不常用,但運用性質去解答其他問題仍是重要考點.這類考點主要考查學生對性質和定義的熟練掌握程度,知識點雖然基礎,但十分重要.

例2設a,b∈R,且a≠2,定義在區間(－b,b)內的函數是奇函數.

(1)求b 的取值范圍;

(2)討論函數f(x)的單調性.

由式①可得

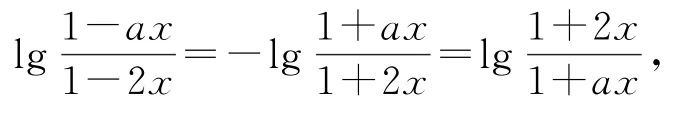
(2)設任意的x1,x2∈(－b,b),且x1＜x2,由b∈可得

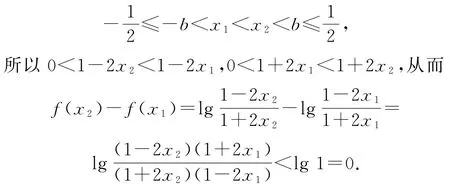
因此,f(x)在(－b,b)內是減函數.

本題第(1)問主要是考查函數的奇偶性,要注意定義域優先考慮的原則.如果僅考慮奇偶性或是僅考慮定義域都不全面,此題需要學生形成全面的解題思維,不要記錯任何定義的法則及要求.第(2)問考查了單調性的判斷與應用.

在函數的學習中,定義是最重要的,我們不能舍本逐末,應該掌握函數形式及其性質的定義,以此為基礎,去解決更為復雜的函數問題.