射影幾何調和點列作圖與阿波羅尼斯圓的聯系

趙臨龍

（安康學院數學與統計學院，陜西安康 725000）

1 問題背景

在射影幾何中，調和點列是最基本也是最重要的概念，是射影幾何理論建立及其研究的重要工具. 如利用調和點列形成的極點與極線概念，是研究二次曲線內在結構的重要工具. 因此，調和點列的幾何作圖成為人們討論的熱點.

在《高等幾何》［1］中，關于調和點列的幾何作圖，先后給出歐式幾何的圓中作圖、仿射幾何的平行線作圖、射影幾何的完全四邊形作圖和射影對應作圖等.

現對于仿射幾何的平行線作圖進行討論.

命題1 如圖1. 已知點列A、B、C，求其調和點列D 滿足（AB，CD）=-1.

作法 如圖1. 在直線AB異側過點C作直線A′B′，使A′C=CB′；連接AA′×BB′=S；過點S 作SD//A′B′交直線AB 于點D. 則點D為所求點，即（AB，CD）=-1.

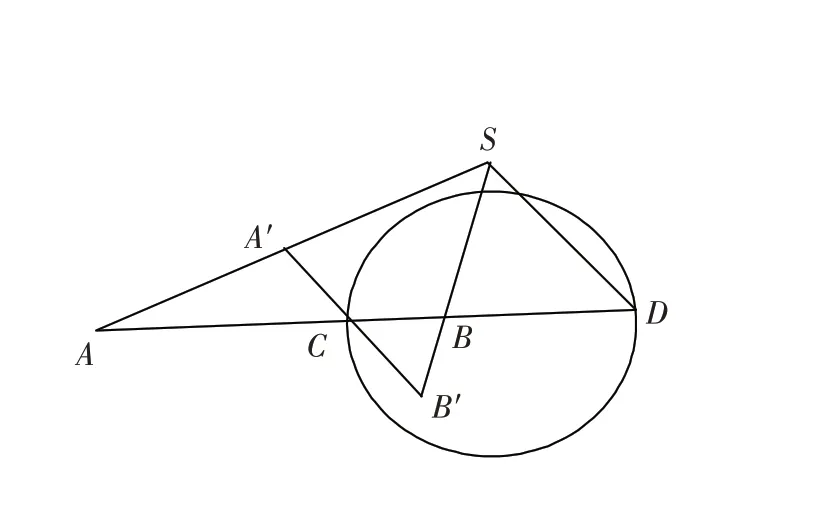
圖1 調和點列的作圖Fig.1 Mapping of harmonic points

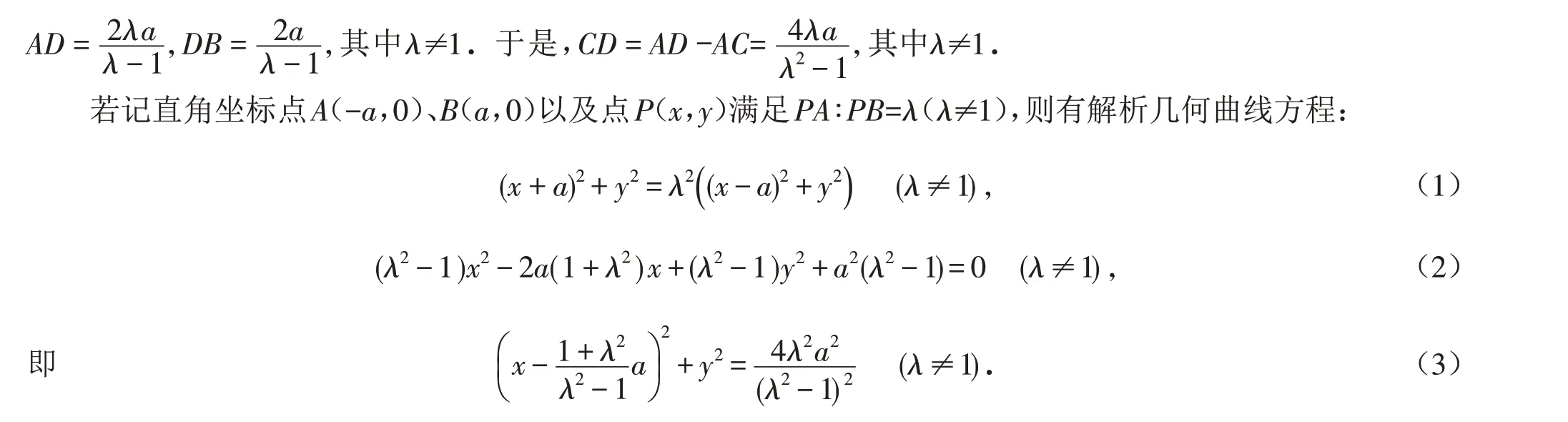
方程（3）的幾何意義是以CD為直徑的圓，該圓在歐式幾何中叫作阿波羅尼斯圓.

命題2［2］（阿波羅尼斯圓）已知兩點A、B，C、D分別為線段AB的定比λ（λ≠1）的內外分點，則以CD為直徑的圓上任意點到A、B兩點的距離之比為λ.

2 問題討論

阿波羅尼斯（Apolloning，約公元前260—170）是古希臘著名的數學家，與歐幾里得、阿基米德一起被稱為亞歷山大時期的數學三巨匠，他對圓錐曲線有深刻而系統的研究，主要的研究成果集中在他的代表作《圓錐曲線》一書中，阿波羅尼斯圓是他的研究成果之一［2］.

推論3 已知兩點A、B，C、D 分別為線段AB 的定比λ（λ≠1）的內外分點，且交點S=AA′×BB′，則點S 在阿波羅尼斯圓上的充分必要條件是AA′∶BB′=λ.

此時，當直線AS 為阿波羅尼斯圓的切線（S 為切點）時，則由圓直徑的對稱性，得到該阿波羅尼斯……