基于量子遺傳算法和模糊C均值聚類的圖像分割

2020-12-10 04:41:24游繼安

湖北工程學(xué)院學(xué)報 2020年6期

劉衣，游繼安

(湖北工程學(xué)院新技術(shù)學(xué)院，湖北孝感 432100)

圖像分割在不同的領(lǐng)域有著非常重要的作用，如醫(yī)學(xué)圖像分割是在醫(yī)療物聯(lián)網(wǎng)領(lǐng)域中自動或半自動化對2D或3D圖像進行邊界檢測的一個重要過程[1]。模糊C均值(fuzzy C means，F(xiàn)CM)聚類方法已被證明是一個很有效的圖像分割的方法[2]，但是它的魯棒性較差，而且對噪聲圖片的分割會很敏感，準確性降低[3]。量子遺傳算法(quantum genetic algorithm，QGA)是韓國人Kuk-Hyun Han最先提出的，它的收斂速度比普通的遺傳算法等要快很多，而且由于量子計算的特征，不容易陷入局部最優(yōu)解的困境[4]。

本文利用量子遺傳算法計算模糊C均值聚類中心，然后得到圖像每個像素點對應(yīng)聚類中心的隸屬度，達到分割的效果。在計算聚類中心時，首先需要選擇隨機樣本。傳統(tǒng)的隨機樣本選擇范圍圖像中的所有像素點，隨機在圖像中選擇一個像素點，得到其灰度值，將其作為某個聚類中心的樣本。但是，不同大小的圖片，像素點個數(shù)范圍變化非常大，對量子遺傳算法中需要使用的種群規(guī)模(染色體個數(shù))、染色體上每個基因的長度，以及進化的代數(shù)，都有著不確定性。如果圖像比較小，而種群規(guī)模或者基因長度過大，則會造成計算冗余，實際測試過程中，發(fā)現(xiàn)長時間都無法得到計算結(jié)果；如果圖像較大，而種群規(guī)模或基因長度相對較小，需要計算的進化代數(shù)就必須增加，搜尋的范圍大了，就很難快速找到最優(yōu)值。對于此問題，本文將圖像的所有像素點的灰度值變化范圍作為尋找聚類中心的樣本空間，可以解決圖像大小不確定的問題，因為任意像素點灰度值變化的最大范圍是0到255，而圖像像素點灰度值變化值不超過255，這樣，就可以使用固定的種群數(shù)量、基因長度和進化代數(shù)來計算，使得算法有很好的魯棒性。

本文利用C++語言和Open CV工具，在Win10系統(tǒng)上使用VS2017進行編程測試，實驗結(jié)果表明本文方法是有效的。

1 QGA簡介

量子疊加態(tài)是QGA的基礎(chǔ)，一個量子比特的疊加態(tài)ψ可以有公式(1)表示：

ψ〉=α0〉+β1〉

(1)

式中：α表示偏向0態(tài)的概率，β表示偏向1態(tài)的概率，α和β之間有公式(2)的關(guān)系：

(2)

QGA的最小單元是一個量子比特，可以用如下向量的形式表示：

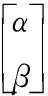
(3)

若一個基因由k個量子比特組成，而一個染色體又由m個基因組成，則一個染色體用矩陣可表示為公式(4)的形式：

(4)

量子的一大特點就是一旦觀測后，每個由α和β構(gòu)成的量子比特疊加態(tài)就立刻隨機變成0態(tài)或者1態(tài)。所以一旦觀測后，基因就變成了二進制形式，最小單位為1個bit，只能取0或1。那么公式(4)代表的染色體的長度(比特總量)就應(yīng)該為k*m。

QGA的步驟如下：

Step 2 測量并存儲坍塌后的二進制數(shù)，將其按照樣本范圍轉(zhuǎn)換為十進制的值；

Step 3 將得到的樣本值帶入適應(yīng)度方程中計算適應(yīng)度的值；

Step 4 篩選最優(yōu)個體，并將其數(shù)據(jù)作為下一代；

while (若當(dāng)前進化代數(shù)t<總進化代數(shù)n) do

begin

Step 2～Step 3;

Step 5 所有染色體基因的所有量子比特經(jīng)過量子旋轉(zhuǎn)門更新α和β；

Step 6 篩選和存儲最優(yōu)個體，滿足下一代必須優(yōu)于或等于上一代；

end

算法運算結(jié)束后，最優(yōu)個體的所有數(shù)據(jù)便知道了。

其中Step 5中提到的量子旋轉(zhuǎn)門，是一個二維矩陣，如公式(5)所示：

(5)

(6)

進一步化簡，可得公式(7)：

(7)

旋轉(zhuǎn)門中的旋轉(zhuǎn)角θi是由偏轉(zhuǎn)角度的絕對值和旋轉(zhuǎn)方向共同決定的，具體關(guān)系如公式(8)所示，其中s(αi，βi)為旋轉(zhuǎn)方向：

θi=Δθi·s(αi，βi)

(8)

公式(8)中的Δθi和s(αi，βi)可以根據(jù)旋轉(zhuǎn)角選擇策略確定，如表1所示。根據(jù)基因中某個位置xi、對應(yīng)位置的最優(yōu)值的bi、該染色體適應(yīng)度是否優(yōu)于最佳染色體適應(yīng)度、αi和βi的值，查詢對應(yīng)的Δθi和s(αi，βi)的值，從而確定θi的值。

表1 旋轉(zhuǎn)角選擇策略

2 FCM算法簡介

模糊C均值的聚類算法，其主要思路是先任意查找聚類中心，然后計算每個樣本對所有聚類中心的隸屬度值，再根據(jù)這個值來更新聚類中心，直到由聚類中心、隸屬度和所有樣本構(gòu)成的目標函數(shù)與上一代相比，相差的絕對值小于某個值，就停止更新，得到最終的聚類中心和所有樣本相對所有聚類中心的隸屬度。

上述算法中提到的目標函數(shù)如公式(9)所示：

(9)

聚類中心Pj和樣本隸屬度uij之間的關(guān)系為公式(10)和公式(11)所示：

(10)

(11)

3 QGA和FCM聚類結(jié)合

3.1 算法結(jié)合意義

結(jié)合兩個算法的目的是為了得到更好的聚類效果，將FCM聚類用于圖像分割上，能較好地辨別聚類效果。所以，主要算法還是FCM聚類，QGA是用來優(yōu)化聚類算法的。

3.2 算法結(jié)合原理

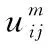
3.3 樣本選取

傳統(tǒng)的FCM圖像分割算法通常將圖像所有像素點的信息當(dāng)作聚類中心的篩選范圍，然后在這里面找聚類中心，單個像素點的信息包括x和y坐標值以及灰度值。對于以公式(9)為適應(yīng)度函數(shù)的QGA，聚類中心篩選范圍的選取也可以用這種方法。這種方式的優(yōu)點是直觀，容易理解，聚類中心就是某個像素點的信息。缺點是不同的圖片大小不一，進而導(dǎo)致樣本量不穩(wěn)定，容易過大或過小，導(dǎo)致對于QGA算法，種群規(guī)模(染色體數(shù))、基因長度和進化代數(shù)都不能設(shè)定為一個常量，算法的魯棒性大大降低。對于大圖片，在尋找聚類中心的過程中，樣本量過大，計算量也過大。

本文提出將圖像所有像素點的灰度值取值范圍作為QGA求聚類中心的樣本范圍，樣本則是范圍里的所有灰度值。這樣，對于任何圖片，最大的樣本范圍也就是0到255，對于不同的圖片，灰度值變化范圍也接近與0到255。這種方法的缺點是樣本點比較抽象，并不是某個具體像素點的信息，而是灰度范圍內(nèi)的任意灰度值，這種方法的優(yōu)點特別突出，因為樣本范圍不會超過0到255的整數(shù)范圍，所有樣本個數(shù)最大也就是256，故采用QGA算法時，種群規(guī)模(染色體數(shù))、基因長度和進化代數(shù)，可以設(shè)為比較小的固定值，計算量明顯減小，經(jīng)過測試，種群規(guī)模可設(shè)為9，每個基因的長度(二進制編碼位數(shù))可設(shè)為6，由于QGA算法的收斂速度非常快，所以最大進化代數(shù)設(shè)為9即可。