恒壓工作模式下光伏發電系統PI參數設計

劉少帥 張曉鋒 夏益輝 李耕

摘? 要： 光伏發電是利用太陽能資源的重要方式，當光伏陣列輸出電能大于負載所需且蓄電池滿充時，光伏發電系統轉入恒壓工作模式。針對光伏電池輸出特性，推出光伏發電系統等效模型，根據恒壓工作模式下系統控制框圖，推導出控制電路傳遞函數，進而分析了光照強度、溫度等環境因素以及元件寄生參數對系統穩定運行的影響，簡化滿足系統穩定運行要求的表達式，并計算出系統穩定時的PI參數范圍。最后，通過Matlab仿真驗證所求PI參數范圍的正確性。

關鍵詞： 恒壓控制; 光伏發電系統; 穩定性; 寄生參數; 傳遞函數; PI參數

中圖分類號： TN02?34; TM914? ? ? ? ? ? ? ? ? ? 文獻標識碼： A? ? ? ? ? ? ? ? ? ? ? 文章編號： 1004?373X（2020）21?0114?05

Design of PI parameter for photovoltaic power generation system

under constant voltage mode

LIU Shaoshuai， ZHANG Xiaofeng， XIA Yihui， LI Geng

（College of Electrical Engineering， Naval University of Engineering， Wuhan 430033， China）

Abstract： Photovoltaic power generation is an important way of solar energy resource utilization. When the output power of the photovoltaic array is greater than the load requirement and the battery is fully?charged， the photovoltaic power generation system is transformed to the constant voltage operation mode. According to the output characteristics of photovoltaic cells， the equivalent model of photovoltaic power generation system is proposed. And then， the transfer function of control circuit is derived on the basis of the system control block diagram under constant voltage operation mode. Furthermore， the influence of environmental factors such as light intensity， temperature and parasitic parameters of components on the stable operation of the system is analyzed， the expression meeting the requirements of stable operation of the system is simplified， and the PI parameter range when the system is stable is calculated. Finally， the correctness of the range of PI parameters is verified by Matlab simulation.

Keywords： constant voltage control; photovoltaic power generation system; stability; parasitic parameter; transfer function; PI parameter

0? 引? 言

光伏發電系統干凈清潔、資源充裕，是新能源發電的重要組成部分[1?3]。為了最大限度地利用太陽能，需要通過控制手段實現光伏發電單元的最大功率跟蹤[4]。然而，當光伏陣列輸出電能大于負載所需且蓄電池滿充時，光伏發電系統轉入恒壓工作模式。光伏陣列的輸出特性與環境因素的變化呈非線性，會影響系統的穩定性，需要通過控制系統進行調節。PI調節器是控制系統的重要組成部分，在工程實踐中，PI調節器通常用來改善系統的穩態性能。PI參數是PI調節器的關鍵環節，對系統穩定性有重要影響。因此，有必要對PI參數的選取展開研究。

通常情況下，在選取PI參數時，往往采用試湊法或者臨界比例度法，不僅盲目性大、效率低，而且采用經驗公式計算的方法誤差大且不能適用于所有情況。有的文獻通過加入零極點[5]或設定穩態性能指標[6?7]求取滿足穩定要求的PI調節器參數，但都僅滿足于某些具體情況，不具有普適性。文獻[8]在建立了包含光伏電池動態模型的小信號模型基礎上，分析了二極管動態電阻對系統穩定性的影響，分別計算出實際情況下、忽略二極管動態電阻情況下以及忽略光伏陣列等效內阻情況下的PI參數范圍，但沒有考慮電器元件寄生參數對系統穩定性的影響。文獻[9]根據調節器參數變化對系統特征值軌跡的影響來設計參數，但是在研究時僅分析單個參數的影響，忽略了各參數之間的耦合關系，無法在整個系統中實現性能最優。文獻[10]針對恒壓模式下，對負載端輸出電壓相同的2個工作點的頻域穩定性進行分析，得出恒壓工作模式下系統工作于電壓源區時穩定性更好。

本文首先推導出光伏發電系統控制電路傳遞函數，然后分析環境因素以及寄生電阻對系統穩定性的影響，簡化滿足系統穩定要求的表達式，并計算出PI參數范圍。最后，通過Matlab仿真驗證所求范圍的正確性。

1? 光伏發電系統結構

光伏電池輸出伏安特性[11]為：

[IPV=ISC-ID-Ish=ISC-Ioexpq（UPV+IPV×Rs）AkT-1-UPV+IPV×RsRsh]

（1）

式中：[IPV]為光伏陣列輸出電流;[ISC]為光生電流源電流;[ID]為光伏電池二極管電流;[Rs]為電池等效串聯電阻;[UPV]為光伏陣列輸出電壓;[Io]為二極管飽和電流;[Rsh]為電池等效并聯電阻;[T]為光伏電池工作絕對溫度值;[k]為玻爾茲曼常量[12]，為1.381×10-23 J/K;[q]為電子的電荷，為1.602×10-19 C;[A]為二極管特性擬合系數。通常，[（UPV+IPV×Rs）Rsh?ISC]，因此忽略[（UPV+IPV×Rs）Rsh]項。式（1）可化簡為：

[IPV=ISC-Ioexpq（UPV+IPV×Rs）AkT-1] （2）

根據式（2），光伏電池等效電路如圖1所示。

圖1中：[C1]為輸入電容;[RC1]為輸入電容寄生電阻;[IL]為電感電流;[L]為變換器升壓電感;[RL]為電感寄生電阻;D為二極管;Q為開關管;[C2]為變換器輸出電容;[RC2]為輸出電容寄生電阻;[Uo]為負載端電壓;[R]為負載端電阻。[Re]為光伏電池等效內阻[13]，表示為：

[Re=UPVISC-IPV] （3）

2? 控制系統結構及穩定條件

2.1? 變換器狀態空間模型及傳遞函數

通過建立系統小信號模型，推導出系統內部變量之間的關系，可為PI參數設計提供參考。光伏發電系統中常用的Boost變換器小信號狀態方程為：

[L?diL（t）dt=uPV（t）-iL（t）RL-（1-D）uo（t）+d（t）UoC1?duC1（t）dt=iSC（t）-uPV（t）Re-iL（t）RC1C1?duC1（t）dt=uPV（t）-uC1（t）C2?duC2（t）dt=（1-D）iL（t）-uo（t）R-d（t）ILRC2C2?duC2（t）dt=uo（t）-uC2（t）] （4）

式中：[iL（t）]，[iSC（t）]，[iPV（t）]，[uPV（t）]，[uo（t）]，[d（t）]分別為[iL（t）]，[iSC（t）]，[iPV（t）]，[uPV（t）]，[uo（t）]，[d（t）]的擾動量。

對式（4）進行拉氏變換可得：

[sLiL（s）=uPV（s）-iL（s）RL-（1-D）uo（s）+Uod（s）sC1uC1（s）=iSC（s）-1ReuPV（s）-iL（s）sRC1C1uC1（s）=uPV（s）-uC1（s）sC2uC2（s）=（1-D）iL（s）-1Ruo（s）-ILd（s）sRC2C2uC2（s）=uo（s）-uC2（s）] （5）

整理可得負載端輸出電壓與占空比之間的傳遞函數為：

[Guod=Uod=A0s4+A1s3+A2s2+A3s+A4B0s4+B1s3+B2s2+B3s+B4] （6）

式（6）中系數表達式如表1所示。

2.2? 控制系統結構及穩定條件

恒壓控制系統結構圖如圖2所示，[Uo，ref]為光伏發電系統負載端參考電壓。該控制系統是單閉環結構，負載端實際輸出電壓與負載端參考電壓作差比較后，經過PI調節器進行調節，再經PWM調制器調整占空比的大小，使負載端實際輸出電壓為參考電壓，從而實現恒壓控制。系統控制結構框圖如圖2所示。

由圖2可得，恒壓工作模式下系統閉環傳遞函數為：

[?o（s）=Fmo?Gpi（s）?Guod（s）1+Fmo?Gpi（s）?Guod（s）] （7）

式中：[Gpi（s）]為PI調節器，[Gpi（s）=kp+kis];[Fmo]為PWM調制器增益，由于恒壓工作模式下光伏陣列的穩定區通常選擇電壓區[9]，[Fmo]取正。根據式（7）可得系統閉環特征方程，再根據勞斯判據即可列寫系統穩定條件表達式。

3? 穩定條件參數分析

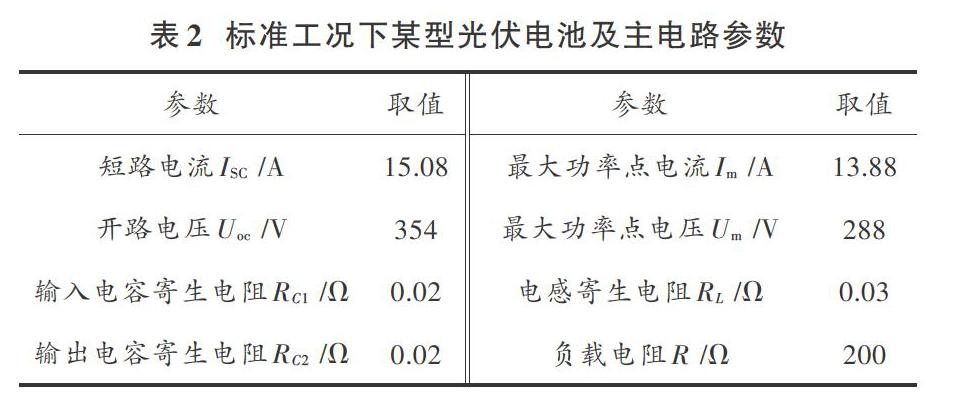
由表1和式（7）可知，要求出滿足系統穩定條件的解析表達式非常困難，不失一般性，采用表2所示參數代入計算，求滿足系統穩定要求的數值解。其參數設置如表2所示。

3.1? 環境因素對系統穩定性影響分析

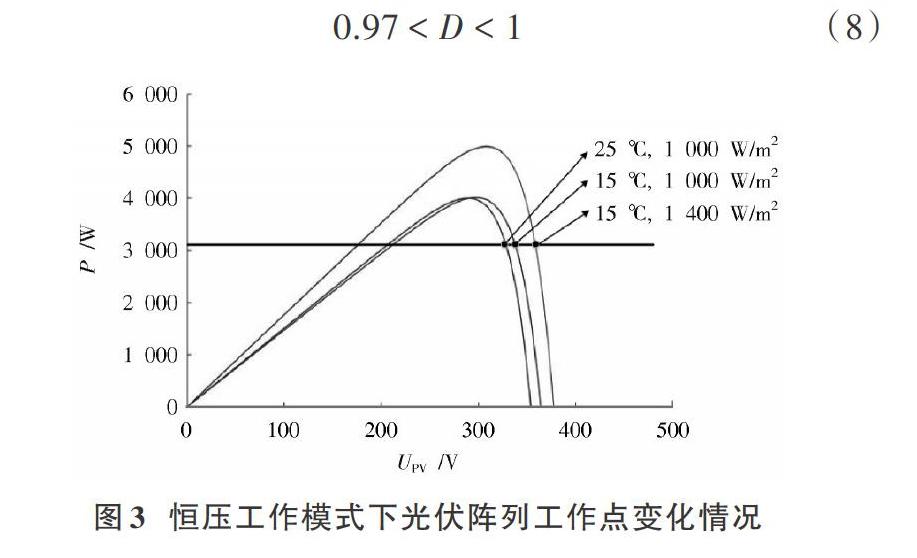
由光伏發電系統輸出特性知，光伏陣列的輸出特性與環境變化不是線性關系。不同光照和環境溫度下，光伏陣列輸出情況如圖3所示。

由圖3知，當負載端輸出電壓恒定時，隨著溫度升高或光照強度變弱，光伏陣列輸出電壓逐漸減小。為便于分析，假設在某一穩態下，[Uo=]400 V，[ISC=]15.08 A，[Fmo=1]，采用表2所示參數和圖2所示控制結構參與計算。經前期試湊可知，當[kp=0.01]，[ki=6]時，光伏發電系統能夠穩定運行于恒壓工作模式。根據勞斯判據，可得系統穩定條件為：

[0.97

當PI參數取其他數值時，可得到[Y1

3.2? 寄生參數對系統穩定性影響分析

為便于分析寄生參數對系統穩定性的影響，假設某一穩態下，[Uo=]400 V，[UPV=]350 V，[D=0.13]，[ISC=]15.08 A，[kp=]0.01，[ki=6]，采用表2所示參數和圖2所示控制結構，將輸入電容寄生電阻值設為變量，可得系統穩定條件為：

[RC1>-0.31 Ω] （9）

當PI參數取其他數值時，得到輸入電容寄生電阻的取值范圍為：[RC1>Y2]，[Y2<0]。即不同穩態PI參數下，系統穩定運行于恒壓工作模式的條件為[RC1]的值大于一個負數，而實際情況下，[RC1≥0]。因此，輸入電容寄生電阻參與系統穩定性計算時，可以假定[RC1=0]。

同樣地，將電感寄生電阻[RL]設為變量，系統穩定條件為：-0.58<[RL]<128.94。換其他PI參數，得到電感寄生電阻的取值范圍為：[Y3]<[RL]<128.94，[Y3]<0。即不同穩態PI參數下，系統穩定運行于恒壓工作模式的條件為[RL]的值大于一個負數且小于128.94 Ω，而實際情況下，[0≤RL?]128.94 Ω。因此，電感寄生電阻參與系統穩定性計算時，可以假定[RL]=0。

將輸出電容寄生電阻設為變量，系統穩定條件為：-0.06<[RC2]<56.78。換其他PI參數，得到輸出電容寄生電阻的取值范圍為：[Y40。即不同穩態PI參數下，系統穩定運行于恒壓工作模式下的條件為[RC2]的值大于一個負數且小于一個正數，而實際情況下，[RC2]≥0。因此，輸出電容寄生電阻參與系統穩定性計算時，可以假定[RC2]=0。

綜上分析，輸入電容寄生電阻、電感寄生電阻、輸出電容寄生電阻參與系統穩定性計算時，均可以假定為0。

3.3? 控制系統PI參數設計

根據3.1節和3.2節分析可知，在最強光照、最低溫度和輸入電容寄生電阻、電感寄生電阻、輸出電容寄生電阻均為0的條件下，設計恒壓工作模式光伏發電控制系統參數，可使系統獲得較好的穩定性。

當輸入電容寄生電阻、電感寄生電阻、輸出電容寄生電阻均為0時，恒壓工作模式控制系統閉環特征方程為：

[RC1C2LReS4+（C1LRe+C2RL-ILLRC1kpRe）s3+[（1-D）2RC1Re+RC2ReL-ILLRC1kiRe+（1-D）RC1ReUokp-ILLRkp]s2+[（1-D）2R+Re-ILRRekp+（1-D）RUokp+（1-D）RC1ReUoki-ILLRki]s+（1-D）RUoki-ILRkiRe=0? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（10）]

假定光照強度最大為1 400 W/m2，溫度最低為15 ℃，某一穩態下光伏發電系統輸出情況為[Uo=]400 V，[UPV=]356 V，[D=]0.11，[Io=]2 A，[R=]200 Ω，[Re]=19.42 Ω。根據勞斯判據，解得系統穩定時PI參數選擇范圍如圖4所示。

4? 仿真驗證

在Matlab/Simulink環境下，采用表2所示參數，搭建光伏發電系統恒壓工作模式下的仿真模型。

4.1? 傳遞函數穩定性計算

在圖4中任取一點，如取[kp=]0.02，[ki=4]，可得此時系統幅值裕度為1.41 dB，相角裕度為2.01°，即幅值裕度和相角裕度均為正。閉環特征方程根分別為[s1=]-553，[s2=]-202，[s3，4=]-37.6±3 400*[i]，即閉環特征方程根均為負。根據自動控制原理理論可知，該PI參數下的系統能夠穩定運行于恒壓工作模式。

4.2? 仿真結果及分析

取[kp=]0.02，[ki=]4，假定光照強度變化范圍為600～1 400 W/m2，溫度變化范圍為15～35 ℃，分別觀察系統在光照強度變化、溫度變化、有無寄生參數時的輸出情況。

假設環境溫度為25 ℃不變，0～0.4 s時，光照強度為1 400 W/m2;0.4～0.8 s時，光照強度為1 000 W/m2;0.8～1.2 s時，光照強度為600 W/m2。圖5a）為光照強度變化時，光伏發電系統負載端輸出電壓波形。假設光照強度為1 000 W/m2不變，0～0.4 s時，環境溫度為35 ℃;0.4～0.8 s時，環境溫度為25 ℃;0.8～1.2 s時，環境溫度為15 ℃。圖5b）為溫度變化時，光伏發電系統負載端輸出的電壓波形。

標準工況下（光照強度為1 000 W/m2，溫度為25 ℃），不考慮寄生參數時，光伏發電系統負載端輸出電壓波形如圖6所示。

在標準工況下考慮寄生參數時，取輸入電容寄生電阻[RC1=]0.02 Ω，電感寄生電阻為[RL=]0.03 Ω，輸出電容寄生電阻[RC2=]0.02 Ω，光伏發電系統負載端輸出電壓波形如圖7所示。

對以上仿真結果進行整理，結果如表3所示。

由表3可知，在最強光照強度和最低溫度條件下計算得到的PI參數能夠在其他光照和溫度條件下保持系統的穩定運行;在不考慮寄生參數情況下計算得到的PI參數能夠適用于含寄生參數電路，與3.1節和3.2節分析結果相吻合。

5? 結? 論

本文分析了環境因素以及寄生參數對系統穩定運行的影響，簡化了滿足系統穩定要求的表達式，計算出系統穩定運行時的PI參數范圍，最后通過Matlab仿真進行驗證。結果表明：

1） 光照強度越強或者溫度越低，系統越不容易穩定，此時計算得到的PI參數能夠在其他光照和溫度條件下保持系統的穩定運行;

2） 輸入電容寄生電阻、電感寄生電阻、輸出電容寄生電阻參與系統穩定性計算時，均可以取0;

3） 通過Matlab仿真驗證可知，計算得到的PI參數范圍能夠滿足恒壓工作模式下光伏發電系統穩定運行的需要。

本文的研究可以增強PI參數選取的科學性，同時，簡化恒壓工作模式下光伏發電系統穩定條件的計算過程，為開展光伏發電系統其他方面的研究打下基礎。

參考文獻

[1] BOROYEVICH D， CVETKOVIC I， DONG Dong， et al. Future electronic power distribution systems a contemplative view [C]// IEEE Conference on Optimization of Electrical and Electronic Equipment. Brasov， Romania： IEEE， 2010： 1369?1380.

[2] 劉念，唐霄，段帥，等.考慮動力電池梯次利用的光伏換電站容量優化配置方法[J].中國電機工程學報，2013，33（4）：34?44.

[3] FEMIA N， FORTUNATO M， VITELLI M. Light?to?light： PV?fed LED lighting systems [J]. IEEE transactions on power electronics， 2013， 28（8）： 4063?4073.

[4] 肖文波，余曉鵬.光伏系統功率跟蹤算法的仿真平臺設計及其實現[J].現代電子技術，2019，42（12）：104?107.

[5] 王生鐵，賈立賓，張計科，等.雙級式光伏并網發電前級變換器系統建模與控制器參數設計[J].可再生能源，2016，34（3）：360?367.

[6] 任明煒，孫玉堂，嵇小輔.數據可視化的LCL型并網逆變器PI參數設計[J].電力電子技術，2016，50（8）：44?47.

[7] 鄭鶴玲，畢大強，葛寶明.光伏模擬系統建模與控制器參數優化[J].電力系統保護與控制，2011，39（18）：49?55.

[8] 秦嶺，謝少軍，羅松.恒壓充電模式下獨立光伏儲能系統的魯棒穩定控制器設計[J].中國電機工程學報，2018，38（12）：3451?3460.

[9] HUANG Hanqi， MAO Chengxiong， LU Jiming， et al. Small?signal modeling and analysis of grid?connected photovoltaic ge?neration systems [J]. Proceedings of the CSEE， 2012， 32（22）： 7?14.

[10] 侯世英，殷忠寧，薛原，等.獨立光伏系統恒壓工作模式下最優工作區的選擇[J].電網技術，2012，36（6）：226?231.

[11] 張興，曹仁賢.太陽能光伏并網發電及其逆變控制[M].北京：機械工業出版社，2018.

[12] 代相波，趙志剛.基于滯環比較的擾動觀測法在光伏MPPT中的研究[J].沈陽工程學院學報（自然科學版），2018，14（1）：5?10.

[13] 楊梅.單相光伏并網逆變系統研究與設計[D].馬鞍山：安徽工業大學，2016.

作者簡介：劉少帥（1992—），男，河南人，碩士研究生，研究方向為電力電子與電力傳動。

張曉鋒（1963—），男，江蘇人，教授，博士生導師，研究方向為電力系統及其自動化、電力電子與電力傳動。

夏益輝（1987—），男，河南人，博士，講師，研究方向為電力電子與電力傳動。

李? 耕（1987—），男，湖北人，博士，講師，研究方向為電力系統運行保護。