基于自適應擴展卡爾曼濾波的消能減震結構及附加阻尼力識別

謝麗宇 李憲之 張睿 薛松濤

摘? ?要：針對消能減震結構中阻尼器提供的阻尼力難以直接測量，對其性能及狀態進行評估較為困難的問題，提出了一種基于自適應擴展卡爾曼濾波的結構參數及未知激勵識別方法，并將其應用于消能減震結構的阻尼器特性識別. 當阻尼器結構模型已知時，該方法可對阻尼器參數進行識別;當阻尼器結構模型未知時，阻尼器對結構提供的附加阻尼力可視為結構所受附加未知激勵，同樣也可由該方法進行識別. 采用一個多層剪切框架結構和一個多層加裝阻尼器的消能減震結構作為數值算例，并采用一個單層加裝阻尼器的剪切框架結構作為試驗算例，驗證了所提出的方法的有效性和可行性. 所提出方法可為消能減震結構中阻尼器的特性識別及性能評估提供更多的依據.

關鍵詞：消能減震結構;附加阻尼力;擴展卡爾曼濾波;自適應

中圖分類號：TU317? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標志碼：A

Identification of a Passively-controlled Energy Dissipation Structure and

Additional Damping Force Based on Adaptive Extended Kalman Filter

XIE Liyu1，LI Xianzhi1，ZHANG Rui1，XUE Songtao1，2?

（1. Department of Disaster Mitigation for Structures，Tongji University，Shanghai 200092，China;

2. Department of Architecture，Tohoku Institute of Technology，Sendai 982-8577，Japan）

Abstract：In order to solve the problems that it is difficult to directly measure the damping force provided by the damper of passive energy dissipation structure， and it is difficult to evaluate the performance and state of the damper， in this paper， a structural identification method based on adaptive extended Kalman filter is proposed and the method is applied to the damper characteristic identification of passive energy dissipation structures. Under the condition that the damper model is known， the damper parameters can be identified; under the condition that the damper model is unknown， the additional damping force provided by the damper can be considered as the unknown excitation and can also be identified by the proposed method. A multi-storey shear frame structure and a multi-storey damper controlled structure are used as numerical examples， and a single-storey damper controlled structure is used as experimental example to demonstrate the effectiveness and feasibility of the proposed method. The proposed method can provide more basis for the characteristic identification and performance evaluation of the dampers in the passive energy dissipation structure.

Key words：damper controlled structure;additional damping force;extended Kalman filters;adaptive

近年來，消能減震結構越來越多地應用在土木工程當中，為提高結構的抗震性能發揮了重要作用. 消能減震結構通常是在結構中安裝阻尼器，由阻尼器吸收、耗散能量，增加結構的耗能能力，從而達到結構控制的目的. 阻尼器相當于結構的“保險絲”，其耗能能力對結構的抗震性能有著重要影響[1-3]. 然而，目前所采用的各類阻尼器在結構中的實際工作性能往往難以直接測定，阻尼器性能下降甚至阻尼器發生破壞都會給結構安全帶來不良影響，如在2011年日本“3. 11”地震中，位于日本宮城縣仙臺市東北工業大學的某棟建筑出現了世界上首例油阻尼器震中破壞的現象[4-5]. 因此，對消能減震結構中阻尼器在實際工程中的工作性能進行研究有著十分重要的意義. 但是，消能減震結構中阻尼器的特性識別一直是一個具有挑戰性的難題，阻尼器結構及作用機理的復雜性使得阻尼器對結構的阻尼力難以準確計算，而且在實際情況下阻尼器提供的阻尼力往往難以準確測量. 這就需要研究一種適用于消能減震結構阻尼器特性的識別方法，以對其模型參數或作用于主體結構的附加阻尼力進行識別[6-7].

卡爾曼濾波方法（KF）[8]是用于系統識別的一種有效算法，最早由Kalman提出，該方法可在部分觀測結構響應的情況下對結構狀態進行有效識別. 近年來有學者對其進行改進，提出了結構參數和結構狀態同時識別的擴展卡爾曼濾波算法（EKF）[9-11]， 此外還有用于結構參數、結構狀態和未知激勵同時識別的未知激勵下擴展卡爾曼濾波算法（EKF-UI）[12-13]、用于強非線性結構識別的無跡卡爾曼濾波算法（UKF）[14]等. 但是這類濾波方法仍需要在一定的限制條件下才能實現良好的追蹤和識別性能，如需要適當的初始條件、準確的參考模型和噪聲分布的完整信息等. 然而，這類信息在實際工程中通常不準確或者不可知，這會導致卡爾曼濾波器性能下降甚至不穩定，使其難以直接用于消能減震結構的阻尼器特性識別.

基于此，本文采用一種改進的自適應擴展卡爾曼濾波方法，對消能減震結構的結構參數、阻尼器參數或附加阻尼力等進行識別. 對于消能減震結構，將其分為阻尼器模型已知與未知兩種情況. 當阻尼器結構模型已知時，采用該方法對阻尼器結構參數進行識別;當阻尼器結構模型未知時，將阻尼器提供的阻尼力視為一種附加未知激勵，并采用所提方法對該附加未知激勵進行識別，即為阻尼器所提供的阻尼力[15]. 該方法采用實際情況下更容易得到的結構動力響應數據對消能減震結構的阻尼器特性進行識別，避免了直接測量結構所受附加阻尼力的困難，可以較好地識別阻尼器特性從而為阻尼器的設計和評估提供依據. 為了驗證所提出方法的可行性，本文采用了一個多層剪切框架結構和一個加裝阻尼器的多層消能減震結構作為數值算例，分別對其結構參數、阻尼器參數或附加阻尼力進行識別，并將其與理論值進行對比. 此外還設計一個單層加裝阻尼器的剪切框架結構試驗對該方法進行驗證，從而說明所提出方法可有效應用于消能減震結構及附加阻尼力識別.

1? ?自適應擴展卡爾曼濾波方法

1. 1? ?擴展卡爾曼濾波方法

一個n自由度結構在外激勵作用下運動方程為：

式中：M為結構質量矩陣;[x]（t），[x] （t），x（t）分別為結構加速度、速度、位移向量;θ為結構參數向量;F [x（t），[x] （t），θ]是與結構參數及位移速度有關的力向量;f（t）為外激勵向量.

當結構所受外激勵已知時，將結構參數θ = （k1，k2，…，kn，c1，c2，…，cn）T擴展到結構狀態向量Z（t） = {xT，[x] T，θT}T中，系統的狀態方程和量測方程可寫成：

式中：w（t）和v（t）代表模型誤差與測量誤差，假設其均值為零，協方差分別為Q（t）與R（t）. 分別對狀態方程和量測方程在Zk-1 = [Z][^]+

k處進行泰勒級數展開可得：

其中，相應的偏導矩陣表示為：

傳統的擴展卡爾曼濾波方法主要有以下幾個步驟，首先是狀態預測：

k的誤差協方差矩陣; Φ k-1≈I + Δt·G k-1為線性系統的狀態轉移矩陣.

接下來使用t = kΔt時刻的觀測信息對預測值進行修正：

k為更新的協方差矩陣.

以上便是傳統擴展卡爾曼濾波方法的主要步驟. 然而，傳統的擴展卡爾曼濾波只能在先驗知識準確的假設下才能實現良好的性能，包括參考模型、噪聲分布和初始條件等.當先驗知識不可用或不準確時，會導致該方法識別性能下降或不穩定[16].

1. 2? ?自適應擴展卡爾曼濾波方法

本文提出了一種具有時變遺忘因子的自適應擴展卡爾曼濾波方法，通過引入的時變遺忘因子λ對誤差協方差矩陣[P][^] -

k進行修改[17-18]，從而增大卡爾曼增益 K k，使更多的舊信息被遺忘，同時，該遺忘因子可不斷調整，使其不至于過大或過小，算法可具有更好的識別能力和穩定性.

式中：Vk 為輸出的誤差協方差矩陣;ρ為衰減因子，本文中選取ρ = 0.95.

當結構所受到的外激勵未知時，未知激勵可由最小二乘法進行估計，相應的流程如下：

式中：[f][^]k為更新的未知外激勵. 以上便是自適應擴展卡爾曼濾波算法的主要步驟.

2? ?數值算例及試驗驗證

為了驗證本文所提出的自適應擴展卡爾曼濾波方法用于消能減震結構識別的有效性，設計兩個數值算例和一個試驗對其進行驗證. 第一個算例為多層剪切框架結構，分別在外激勵已知與外激勵未知情況下對其進行識別. 第二個算例為加裝阻尼器的多層消能減震結構，將其分為阻尼器模型已知與阻尼器模型未知兩種情況，在阻尼器模型已知情況下對阻尼器參數進行識別，在阻尼器模型未知情況下對阻尼器提供的附加阻尼力進行識別. 試驗設計為單層加裝阻尼器的剪切框架結構，在阻尼器模型未知情況下對阻尼器提供的附加阻尼力進行識別.

2. 1? ?多層剪切框架算例

算例模型為5層剪切框架結構（見圖1），結構參數為各層質量m1～5=300 kg，層間剛度k1～5=15 000 N/m，層間阻尼c1～5 = 100 N·s/m. 結構受EL-Centro地震波作用，選取50 s進行加載，采樣時間間隔為0.02 s，地震激勵的加速度峰值為0.2g = 1.96 m/s2. 在外激勵信息已知情況下，僅觀測結構第2、3、5層的加速度響應，并且該加速度響應信息包含2%的噪聲. 識別結果如圖2～圖5所示.

由識別結果可知，對于剪切框架結構，在已知外激勵情況下，自適應的擴展卡爾曼濾波方法可準確識別出結構的位移、速度等運動狀態及結構的阻尼、剛度等參數. 此外該方法具有良好的抗噪性，在加噪2%情況下仍能對結構進行準確識別，而且僅需部分觀測. 在未知外激勵的情況下，該方法同樣可對結構狀態和結構參數進行準確識別，并且能識別出作用在結構上的未知外激勵信息，因此，該方法可較好地用于結構系統及輸入同時識別.

2. 2? ?多層消能減震結構算例

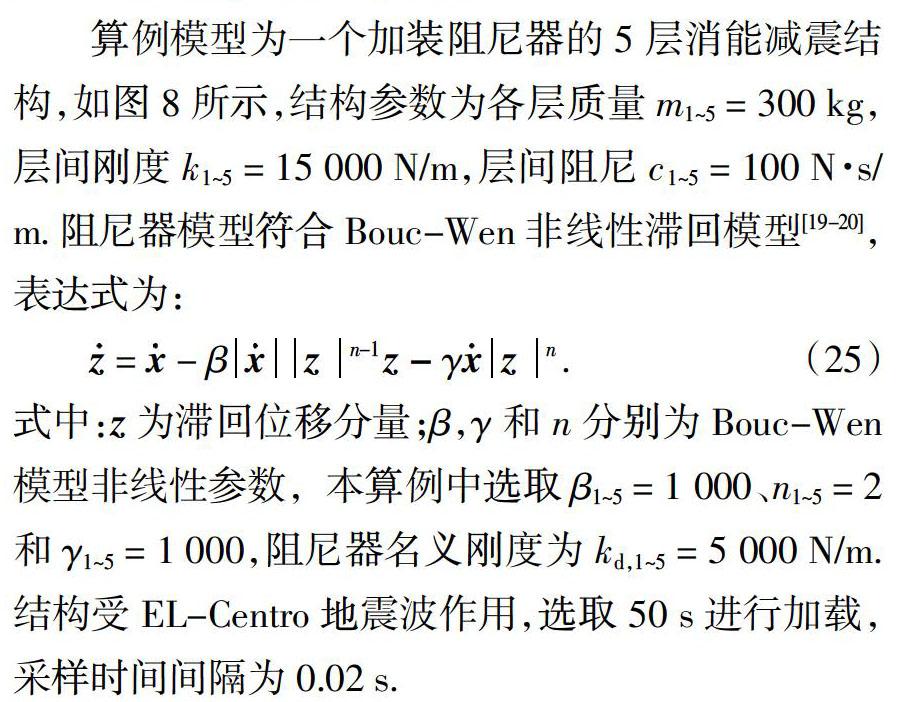
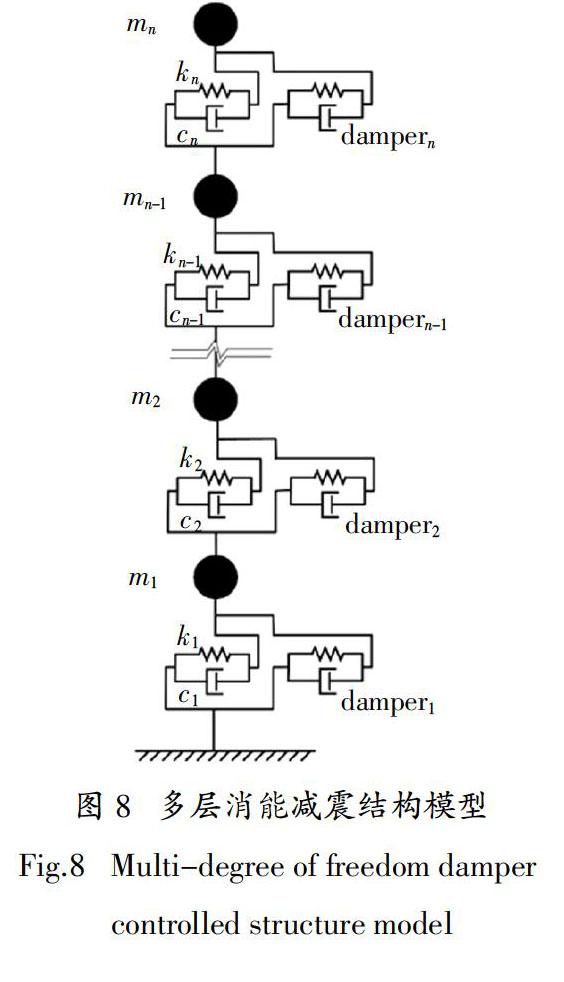
算例模型為一個加裝阻尼器的5層消能減震結構，如圖8所示，結構參數為各層質量m1～5 = 300 kg，層間剛度k1～5 = 15 000 N/m，層間阻尼c1～5 = 100 N·s/m. 阻尼器模型符合Bouc-Wen非線性滯回模型[19-20]，表達式為：

式中：z為滯回位移分量;β，γ和n分別為Bouc-Wen模型非線性參數，本算例中選取β1～5 = 1 000、n1～5 = 2和γ1～5 = 1 000，阻尼器名義剛度為kd，1～5 = 5 000 N/m. 結構受EL-Centro地震波作用，選取 50 s進行加載，采樣時間間隔為0.02 s.

在阻尼器模型已知情況下，觀測結構的各層加速度及位移響應，對結構參數及阻尼器參數進行識別. 以第4層為例，識別結果如圖9～圖13所示.

在阻尼器模型未知情況下，阻尼器對結構提供的阻尼力可被視為作用于結構上的附加未知激勵，該附加激勵可由適用于未知激勵情況下的自適應擴展卡爾曼濾波方法識別出來，即為阻尼器對結構所提供的阻尼力.相應的結構參數、結構狀態及附加阻尼力識別結果如圖14～圖16所示. 結構參數及結構狀態識別誤差見表1.

通過識別附加阻尼力與理論阻尼器提供阻尼力進行對比，可以說明所提出的方法在阻尼器模型未知情況下可以有效識別出阻尼力，同時能夠識別出結構的剛度、阻尼等結構參數，其中結構剛度的識別情況優于阻尼識別情況，最大誤差不超過1%. 此外，對于結構位移、速度等結構狀態，也可以進行準確識別.

2.3? ?試驗驗證

為了驗證所提出方法的有效性與可行性，設計了單層帶阻尼器的鋼框架結構試驗. 試驗裝置如圖17所示，該單層鋼框架高為1 m，樓板與柱均采用Q235鋼板，樓板尺寸為834 mm × 390 mm，厚度為10 mm，柱尺寸為1 000 mm × 100 mm，厚度為3 mm，結構質量為23.0 kg.

試驗測量裝置主要包括3個部分：加速度傳感器、激光位移傳感器以及力傳感器，布置位置如圖17所示. 其中加速度傳感器采用PCB333B30型加速度計，靈敏度100 mV/g，測量量程50g，頻率范圍0.5～3 kHz. 位移傳感器采用基恩士IL300型激光位移傳感器，測量量程為160 ～ 450 mm. 力傳感器采用上海力恒LH-S09A微型拉壓力傳感器，量程為500 N，靈敏度為1.897 6 mV/N. 試驗中，信號采樣頻率均為1 000 Hz.

對結構頂部施加80 mm初始位移，帶阻尼器框架結構可進行自由振動，由加速度傳感器與位移傳感器可獲得結構頂部加速度響應及位移響應，作為試驗觀測值.與結構相連的阻尼器為拉索式電渦流慣容阻尼器，其作用在主體結構上的附加阻尼力可由阻尼器與上部鋼板相連的鋼絞線上的力傳感器測出. 對結構參數及在兩種不同工況下的附加阻尼力的識別如圖18～圖21所示.

單層帶阻尼器鋼框架結構的試驗結果表明，所提出的方法可有效識別出結構的剛度、阻尼等結構參數，并且識別出的阻尼器提供給結構的附加阻尼力與傳感器實測結果符合較好，從而說明了所提出方法用于消能減震結構及附加阻尼力識別的可行性.

3? ?結? ?論

1）本文提出一種改進的自適應擴展卡爾曼濾波算法，可適用于外激勵已知與外激勵未知兩種情況下的結構參數識別，而且在未知激勵的情況下可對結構參數及未知激勵同時進行識別.

2）將消能減震結構的識別分為阻尼器模型已知與未知兩種情況，當阻尼器結構模型已知時，采用該方法對阻尼器結構參數進行識別;當阻尼器結構模型未知時，將阻尼器提供的阻尼力視為一種附加未知激勵，并采用所提方法對該附加未知激勵進行識別，即為阻尼器所提供的阻尼力.

3）該方法可有效用于消能減震結構的識別，通過實際情況下較容易得到的結構動力響應數據對阻尼器參數或阻尼器提供的阻尼力進行識別，可避免直接測量結構所受附加阻尼力，為阻尼器的設計和評估提供更多依據.

參考文獻

[1]? ? 林新陽，周福霖. 消能減震的基本原理和實際應用[J]. 世界地震工程，2002，18（3）：48—51.

LIN X Y，ZHOU F L. Theory and application of energy dissipation seismic reduction technology [J]. World Earthquake Engineering，2002，18（3）：48—51. （In Chinese）

[2]? ? 謝麗宇，唐和生，薛松濤. 減振高層建筑的極限破壞及性能再生的研究現狀及前景[J]. 結構工程師，2014（3）：205—212.

XIE L Y，TANG H S，XUE S T. State-of-the-art and future trend in limit state and rehabilitation of vibration-controlled high-rise buildings [J]. Structural Engineers，2014（3）：205—212. （In Chinese）

[3]? ? 梅真，郭子雄. 磁流變阻尼器減振結構振動臺試驗與動力可靠性分析[J]. 湖南大學學報（自然科學版），2017，44（7）：46—53.

MEI Z，GUO Z X.? Shaking table test and dynamic reliability analysis of structures with MR dampers [J]. Journal of Hunan University （Natural Sciences），2017，44（7）：46—53. （In Chinese）

[4]? ? XIE L Y，CAO M，FUNAKI N，et al. Performance study of an eight-story steel building equipped with oil dampers damaged during the 2011 Great East Japan Earthquake Part 1：structural identification and damage reasoning [J]. Journal of Asian Architecture and Building Engineering，2015，14（1）：181—188.

[5]? ? CAO M，XIE L Y，TANG H S，et al. Performance study of an 8-story steel building equipped with oil damper damaged during the 2011 Great East Japan Earthquake Part 2：novel retrofit strategy[J]. Journal of Asian Architecture and Building Engineering，2016，15（2）：303—310.

[6]? ? MASRI S F，CAFFREY J P，CAUGHEY T K，et al.? Identification of the state equation in complex non-linear systems [J]. International Journal of Non-linear Mechanics，2004，39（7）：1111—1127.

[7]? ? 宋琛琛，謝麗宇，薛松濤. 基于非線性阻尼系統解耦的消能減震結構系統識別[J]. 地震工程與工程振動，2015，35（5）：161—166.

SONG C C，XIE L Y，XUE S T.? System identification of energy dissipating structure based on decoupling nonlinear damping system [J].? Earthquake Engineering and Engineering Dynamics，2015，35（5）：161—166. （In Chinese）

[8]? ? KALMAN R E.? A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering，1960，82（1）：35—45.

[9]? ? GHAHARI S F，ABAZARSA F，GHANNAD M A，et al.? Response-only modal identification of structures using strong motion data [J]. Earthquake Engineering & Structural Dynamics，2013，42（8）：1221—1242.

[10]? 雷鷹，倪萍禾，劉朝. 有限觀測絕對加速度響應下剪切框架在未知地震作用下損傷診斷[J]. 振動與沖擊，2012，31（6）：96—99.

LEI Y，NI P H，LIU C. Structural damage detection of a shear building under unknown earthquake excitation with limited observations of absolute acceleration responses[J]. Journal of Vibration and Shock，2012，31（6）：96—99. （In Chinese）

[11] HOSHIYA M，SAITO E. Structural identification by extended Kalman filter[J]. Journal of Engineering Mechanics，1984，110：1757—1771.

[12]? LIU L，SU Y，ZHU J，et al. Data fusion based EKF-UI for real-time simultaneous identification of structural systems and unknown external inputs[J]. Measurement，2016，88：456—467.

[13]? YANG J N，LIN S，HUANG H，et al. An adaptive extended Kalman filter for structural damage identification[J]. Structural Control & Health Monitoring，2010，13（4）：849—867.

[14]? JULIER S J. Unscented filtering and nonlinear estimation[J].? Proceedings of the IEEE，2004，92（3）：401—422.

[15]? 張睿，謝麗宇，薛松濤，等. 基于卡爾曼濾波的消能減震結構附加阻尼力識別[J]. 建筑結構，2018，48（S2）：441—445.

ZHANG R，XIE L Y，XUE S T，et al. Kalman filter based structural additional damping force identification for damper controlled structures [J]. Building Structure，2018，48（S2）：441—445. （In Chinese）

[16]? YANG J N，LIN S. On-line identification of non-linear hysteretic structures using an adaptive tracking technique[J]. International Journal of Non-Linear Mechanics，2004，39（9）：1481—1491.

[17]? 穆騰飛，周麗. 輸入未知條件下基于自適應廣義卡爾曼濾波的結構損傷識別[J]. 振動工程學報，2014，27（6）：827—834.

MU T F，ZHOU L. Structural damage identification using adaptive extended Kalman filter with unknown inputs [J]. Journal of Vibration Engineering，2014，27（6）：827—834. （In Chinese）

[18]? 張浩. 基于強跟蹤無跡卡爾曼濾波的結構時變參數識別[D]. 蘭州：蘭州理工大學土木工程學院，2016：17—22.

ZHANG H. Structural time-varying parameter identification based on strong tracking unscented Kalman filter[D]. Lanzhou：College of Civil Engineering，Lanzhou University of Technology，2016：17—22. （In Chinese）

[19]? WEN Y K.? Methods of random vibration for inelastic structures [J].? Applied Mechanics Reviews，1989，42（2）：39—52.

[20]? 程驕陽，許斌，賀佳. 基于部分加速度測量的結構Bouc-Wen非線性恢復力及質量識別[J]. 噪聲與振動控制，2018，38（2）：179—187.

CHENG J Y，XU B，HE J. Identification of Bouc-Wen nonlinear restoring force and mass of structures with limited acceleration measurements [J]. Noise and Vibration Control，2018，38（2）：179—187. （In Chinese）