基于等參映射與改進折半法的公路車橋耦合分析系統

趙越 黃平明 劉修平 韓萬水 毛旺濤

摘? ?要：針對傳統全耦合車橋耦合分析計算量大、效率低的問題，基于等參映射及改進折半法建立公路車橋耦合分析系統. 采用ANSYS建立橋梁有限元模型，利用MATLAB建立多種精細化車輛動力分析模型，采用全過程迭代法分別求解橋梁子系統與車輛子系統. 為實現車輪荷載快速自動加載，引入四邊形等參映射和改進折半查找法確定車橋接觸點的插值系數和加載位置. 基于彈簧-質量模型過簡支梁算例及某大跨懸索橋行車試驗，將該分析系統與經典數值分析方法、實測數據以及傳統的時間步迭代方法進行對比. 研究結果表明，所建立的車橋耦合分析系統具有較好的分析精度和計算效率，迭代過程收斂速度較快，可為高流量、高隨機車輛荷載下橋梁結構空間響應分析提供參考.

關鍵詞：橋梁;車橋耦合分析;有限元模型;全過程迭代;改進折半查找;等參映射

中圖分類號：U445.446? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標志碼：A

Highway Vehicle-bridge Interaction Analysis System Based on

Isoparametric Mapping and Improved Binary Search

ZHAO Yue，HUANG Pingming?，LIU Xiuping，HAN Wanshui，MAO Wangtao

（School of Highway，Changan University，Xian 710064，China）

Abstract：To reduce the computing work and improve the efficiency of vehicle-bridge coupling analysis when using traditional fully coupled method， a high efficiency highway vehicle-bridge interaction analysis system was established based on improved binary search and isoparametric mapping. The finite element model of the bridge was simulated using ANSYS， the multiple refined dynamic vehicles were modeled in MATLAB， and the inter-history iteration method was used to analyze the bridge subsystem and vehicle subsystem separately. The quadrilateral isoparametric mapping and improved binary search method were introduced for quick determination of interpolation coefficient and loading position of vehicle-bridge contact point to realize the quick automatic loading of wheel load. Based on the spring-mass model passing through a simply supported beam and a running test of a long-span suspension bridge， the proposed analysis system was compared with the classical numerical analysis method， measured data and traditional time step iteration method. The results show that the proposed analysis system exhibits a good computing efficiency and accuracy and rapid convergence， which can provide a reference for the bridge spatial response analysis under large and highly random traffic flow.

Key words：bridge;vehicle-bridge interaction analysis;finite element model;inter-history iteration;improved binary search;isoparametric mapping

車橋間的耦合作用不僅會影響到橋梁結構的安全性和適用性，還會影響行車安全和舒適性. 近年來，橋梁結構形式的多樣化、汽車速度和載重的不斷加大使得車橋之間的相互作用愈發復雜和不確定，車橋耦合振動問題受到了國內外學者的廣泛關注[1-4].

車橋耦合振動的分析方法主要包括3種：解析法、試驗研究法和數值模擬法[5]. 解析法雖然是理論推導，比較嚴謹，但當橋梁幾何特征和材料特性有限制條件時，在方程建立過程中不可避免地要對實際條件進行簡化，而且有些復雜方程無法得到解析解，所以解析法在實際工程中運用有一定的局限性[6]. 試驗法雖然能客觀且綜合地反映橋梁在車輛動載作用下的實際工作情況，但由于人力、物力消耗較大且操作難度高，實現起來并不經濟. 目前數值模擬憑借易實現、低成本等特點已成為車橋耦合振動的主要分析手段. 早期的數值模擬法大多是基于Visual C++或Visual Fortran的自主研發分析系統[7-8]，以自編的程序計算橋梁系統的響應. 隨著各種大型通用商業有限元分析軟件的開發，其前處理模塊中，橋梁上、下部結構和附屬結構等均可選用不同的單元類型來模擬，在求解過程中也能兼顧結構的幾何非線性和材料非線性，以此為基礎的各種數值方法[9-13]成為模擬分析車橋耦合振動問題的行之有效的工具.

基于數值方法進行車橋耦合分析系統編制主要包括基于模態疊加法及基于全耦合理論兩種[14].相比于后者，模態疊加法簡單實用，但結構高階模態的提取較難，分析結果的精度易受影響[15]. 基于全耦合方法的車橋耦合分析物理意義明確，分析精度相對較高，但由于車輛對橋梁結構每一時步的加載求解均需借助復雜的迭代過程，故分析效率相對較低，尤其是在分析高流量、高隨機車流作用下大跨徑橋梁的結構動力響應問題時，將面臨較高的時間成本問題[16]，因此提高車橋耦合分析運算效率已成為當前國內外學者的一個研究方向[17]. 例如張楠等[18]提出了基于全過程迭代的車橋耦合動力分析方法，可通過人為干預促進計算收斂，相比傳統的時間步迭代方法，總求解次數大幅減少. 李巖等[19]提出了一種維度時變的隨機車流與橋梁耦合振動分析方法，使得振動方程單步的求解維度降低，既保持了整體法計算穩定的特點，又有效提高了計算效率. Chen等[20]則通過將隨機車流等效為移動荷載列的方法，達到了降低計算成本的目的. 總體來看，車橋耦合分析系統可以從橋梁模型、荷載模型以及計算方法上進行優化.

本文以優化確定車橋接觸點的插值系數和加載位置為出發點，引入了四邊形等參映射和改進折半查找法提高公路車橋耦合分析系統的計算效率. 首先，采用MATLAB語言建立公路橋梁典型車輛動力分析模型，基于ANSYS建立橋梁有限元模型;其次，采用全過程迭代法分別求解得到橋梁和車輛的運動狀態，通過程序間的接口調用施加車橋間作用力，期間引入四邊形等參映射和改進折半查找法并控制時步輸出結果以提高車橋耦合運算效率;最后通過經典數值算例和實橋應用對比驗證所建立的分析系統的準確性和實用性.

1? ?基于等參映射與改進折半法的車橋耦合分

析系統建立

1.1? ?車輛模型

汽車車輛一般由車體、車輪等構件以及連接這些構件的減震系統、懸掛系統組成，根據車橋耦合振動分析的需要對車輛模型進行簡化，將車輛模擬為剛體的組合，剛體之間通過軸質量塊、彈簧元件和阻尼元件相互連接，不同車型所對應的車輛動力分析模型不同. 根據課題組前期研究成果，目前公路常見車輛按照車輛軸數、輪數、軸距、軸重等數據可劃分為5大類，17個車型[21-23]. 采用MATLAB語言，針對17種車型分別建立相應的車輛動力分析模型.

在車輛動力分析模型建立過程中，車輛被劃分為不同的剛體部件，如車體、車輪等. 空間內單一剛體具有3個方向的平動和3個方向的轉動自由度. 在車輛勻速直線前進時，剛體部件沿著車輛前進方向的振動對橋梁的豎向及橫向振動影響不大，因此各剛體沿車體運動方向的自由度可忽略，此時車體具有5個自由度：豎向、橫向、點頭、側滾和搖頭，每個車輪具有橫向和豎向2個自由度，拖掛式車型不考慮橫移和搖頭這2個自由度，每個車體具有浮沉、點頭及側滾3個自由度，每個車輪只有豎移一個自由度.

圖1以三軸車（雙后軸）為例，給出了相應的動力分析模型立面及側面圖. 其中，K i

1.2? ?車橋運動方程及求解策略

車橋耦合系統的動力方程可表示為：

式中：Mv、Cv、Kv分別為車輛系統的總體質量矩陣、總體阻尼矩陣及總體剛度矩陣;Mb、Cb、Kb分別為橋梁系統的總體質量矩陣、總體阻尼矩陣及總體剛度矩陣;Zv、Zb分別為車輛、橋梁系統的位移向量;Fv、Fb分別為車輛、橋梁系統的荷載向量.

在車輛運行過程中，假設車輪始終與橋面接觸，橋梁振動引起的橋梁豎向位移將引起車輛減震系統、懸掛系統的變形，且路面粗糙度也是車橋耦合體系的主要激勵源之一，因此車橋系統之間的相互作用力既是車輛和橋梁系統運動狀態Zv、Zb的函數，也是路面粗糙度Ra的函數，則車橋耦合系統的運動方程可進一步表示為：

聯立式（1）與（2），對車輛與橋梁兩個子系統建立耦合關系. 采用全過程迭代法分別求解橋梁子系統和車輛子系統，主要迭代過程通過MATLAB編制相應運算程序予以實現，期間由基于ANSYS的橋梁有限元模型及相應分析過程提供響應輸出，具體流程如圖2所示，收斂準則定義為‖F i

v? ? ?‖<0.1. 全過程迭代法每一步均為全時程計算，具有思路清晰明確、易于操作、計算準確、占用內存少等優點.

1.3? ?基于等參映射的接觸點荷載分配

目前橋梁結構橋面模擬有限元模型多為梁格模型、實體或板殼單元模型，車輪荷載一般簡化為集中力并分配至相鄰4個節點，如圖3所示. 在二維平面內四邊形荷載分擔方式與位移插值函數一致. 當車輪荷載作用于某一位置（x，y）時，相應的等參映射關系如圖4所示.

坐標映射關系為：

式中：x、y是車輪荷載與橋面接觸點坐標;xi、yi分別為四邊形單元的第i個節點的橫、縱位置;ξ、η為x、y映射到母單元的值;ξi、ηi分別為母單元的第i個節點的橫、縱位置，是已知量;Ni（ξ，η）為等參映射點（ξ，η）的函數[24];函數值Ni為四邊形單元的第i個節點的荷載分配系數.

雙線性方程組（3）的未知量ξ和η可通過牛頓迭代法[25]求解，進而計算出分配系數Ni，實現車輪荷載的自動加載. 迭代過程為：

1.4? ?基于改進折半法的快速加載

為實現車輪荷載的快速自動加載，需定位臨近4個節點的位置信息，折半查找法作為一種在有序數組中查找某一特定元素的搜索算法，通過不斷將查找范圍減半提高搜索效率，本文將折半法查找確定值的思想擴展到查找車輪作用區間范圍上. 折半查找的前提條件是必須將搜索目標范圍排成有序數列，雖然折半查找效率高，但排序本身又增加了一定工作量. 橋梁結構模型的特點決定了同一計算過程中，主梁節點一經確定便不再改動，因此全部計算過程僅需一次排序，后續所有車輪作用范圍的確定均可直接使用，從全局角度考慮可有效提高查找效率.

以車輪縱向加載點x處的臨近坐標定位為例，橫向加載點y處臨近點查找與之類似，查找流程如圖5所示，具體步驟如下：

1）導入ANSYS模型中待求車輛所在車道上全

部單元的節點坐標，按照升序排列形成一維矩陣t.

2）初始化：計算一維矩陣的大小確定last，令front = 1.

3）計算mid=round（（front+last）/2），round表示四舍五入.

4）如果mid=last，那么查找結束，車輪x處于一維矩陣t的上限位置是mid，下限位置是mid-1. 否則，判斷車輪x的值是否介于一維矩陣t的front和mid位置之中，若是，則令last=mid，否則令front=mid.

5）繼續步驟3），直到mid=last.

確定車輪荷載作用點的臨近4個節點后，通過牛頓迭代法求解方程（3），繼而可得到每個節點處的插值系數，從而確定荷載分配值. 為減少車橋耦合計算工作量和提高程序運行效率，僅將荷載作用點的位移和速度輸出，利用已知的插值系數計算出車輪處的速度和位移，用于車橋作用力的求解中.

2? ?數值算例驗證

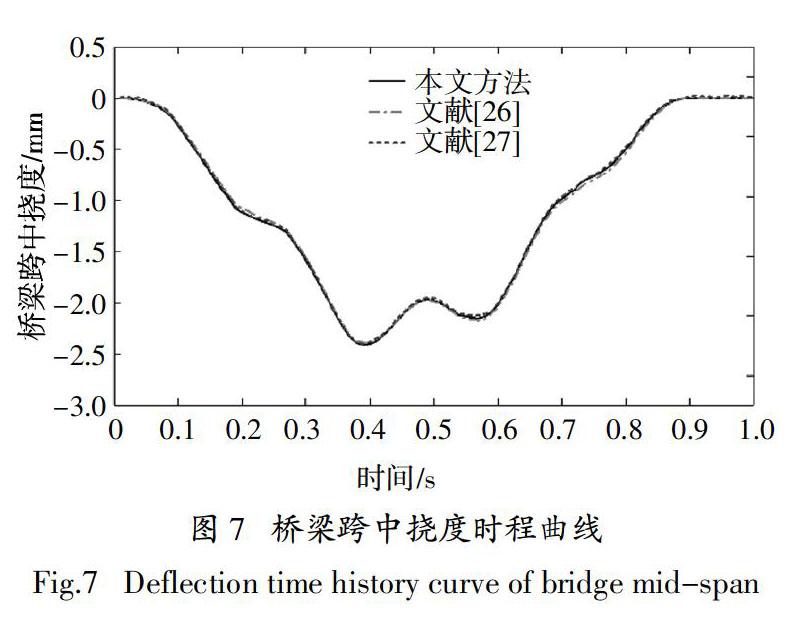
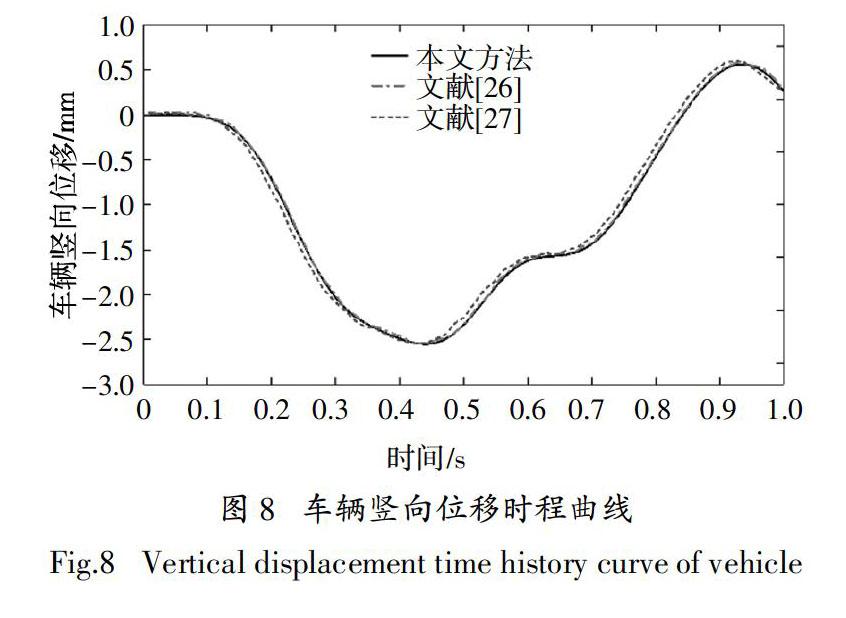
為初步驗證本文建立的車橋耦合分析系統的準確性，首先基于數值分析算例進行對比. 由于復雜橋梁的數值分析結果較難得到，故以經典的單自由度彈簧-質量模型通過簡支梁橋為例，將所建立系統分析結果與文獻[26-27]分析結果進行比較. 算例信息如圖6所示，簡支梁全長25 m，橋梁有限元模型由100個BEAM4單元組成. 截面慣性距2.9 m4，彈性模量2.87 × 109 kN/m2，線密度2 303 × 103 kg/m，泊松比0.2，車輛質量5.75 t，彈簧剛度1 595 × 103 N/m，移動速度v = 27.78 m/s，不考慮阻尼和路面不平整度.

橋梁基頻有限元計算值4.779 Hz，理論值4.78 Hz，二者非常接近. 橋梁的跨中撓度時程曲線及車輛豎向位移時程曲線如圖7和圖8所示，車輛豎向加速度時程曲線如圖9所示，車橋接觸力時程曲線如圖10所示. 根據結果可知，采用本文方法計算的曲

線與文獻[26-27]中的曲線吻合良好. 車輛豎向加速度時程曲線與車橋接觸力時程曲線變化趨勢相同，初步說明所建立分析系統的分析精度滿足基本要求.

3? ?實橋驗證與應用

3.1? ?橋梁信息

四渡河大橋是滬蓉國道主干線湖北宜昌至恩施高速公路的控制性工程，是一座主跨900 m的鋼桁梁懸索橋. 主梁總寬度為26.0 m，橋面凈寬為24.5 m，采用雙向四車道布置，單向2.41%縱坡. 加勁梁由主桁架、上下平聯、橫向桁架組成，主桁架采用華倫式鋼桁加勁梁. 為了減小主梁與主纜相對運動導致的吊桿彎曲應力，橋梁的跨中位置設置剛性中央扣以減弱單向縱坡帶來的影響. 橋梁信息如圖11所示.

基于梁格理論采用ANSYS建立該橋梁有限元模型，模型建立過程中，將車道所處的橋面等效為4根縱梁，縱梁、弦桿、腹桿等用BEAM4單元模擬，主纜、吊索用LINK10單元模擬. 為保證模型的準確性，已根據模態實測數據對初始有限元模型進行了修正[28]. 根據已有研究成果，新建高速公路橋梁橋面不平整度基本為ISO標準中的A級路面[29-30].因此，根據相關標準參數生成如圖12所示的路面不平整度.

3.2? ?基于實測數據的分析系統驗證

進一步采用該橋梁對所建立的分析系統開展驗證工作，首先設置車輛過橋測試工況，具體工況信息包括：1）兩輛三軸卡車以20 km/h車速勻速過橋;2）兩輛三軸卡車以50 km/h車速勻速過橋. 測試工況中車輛行駛位置及動應變測點如圖13所示，動應變測點布設于中央扣處主桁上弦桿上. 兩輛三軸車所對應的車輛動力模型參數及質量參數如表1所示[31].

采用基于等參映射與改進折半法所建立的車橋耦合分析系統對上述兩個測試工況進行分析，并提取與測點位置相應單元的應變信息，實測結果與理論分析結果的對比如圖14、圖15所示. 由圖14和圖15可知，基于所建立車橋耦合分析系統所得到的分析結果能夠與實測結果良好地吻合，20 km/h和50 km/h車速下跨中應變峰值誤差分別為1.3%和0.31%，說明所建立的車橋耦合分析系統分析精度能夠滿足要求. 應變峰值出現誤差不同的主要原因在于行車試驗有一定的隨機性，車橋耦合分析計算中將試驗車輛車速確定為一個定值，但實際車輛難以精確保持在預定車速，并且車輛在橋上的運行位置亦會產生輕微的變化，對結構的振動響應產生影響，因此導致出現應變峰值誤差不同的情況.

3.3? ?計算效率分析

圖16給出了本文所建立分析系統在上述2個測試工況下的迭代進程，可見，盡管2種車速下所建立分析系統在初始階段迭代收斂誤差很大，但經過3次迭代后迅速下降，能夠在第6次迭代后達到收斂狀態. 為進一步分析該分析系統在求解過程中對分析效率的提升情況，現針對算例采用基于時間步迭代的傳統分析方法與本文分析方法進行對比，計算2輛卡車以60 km/h車速雙車并行工況下結構的響應. 由于本文所提出方法優勢在于占用系統計算資源少，為體現本文方法相比傳統方法提升效果，選取在相同計算機配置情況下2種方法計算時長作為體現計算效率的指標. 全部計算采用常規辦公用計算機，主要配置為處理器6核6線程，主頻2.8 GHz，內存8 GB.

首先對比兩種方法所得到的橋梁跨中豎向加速度和位移響應，如圖17所示. 可知基于時間步迭代的傳統分析方法與本文方法所得結果基本相同. 加速度及位移變化趨勢基本一致，峰值相對誤差分別為0.1%和0.22%.

表2給出了兩種分析方法計算耗時信息. 可見兩種方法總時間步均為543，總迭代次數相仿，但本文方法通過結合全過程迭代，引入等參映射及改進折半法，實現了車輪作用點臨近節點快速定位及自動加載，在保證計算精度的同時，較傳統方法求解總耗時減少了42.5%. 盡管對于當前目標結構，計算總耗時并不很長，但該分析方法對于進一步進行高強度隨機車流下橋梁結構空間動力響應分析具有積極意義，可有效減少高流量及高隨機車輛荷載作用時的計算耗時，有較高的計算效率.

4? ?結? ?論

針對基于傳統全耦合理論開展公路車橋耦合分析效率偏低的問題，在車橋耦合分析系統建立過程中引入等參映射進行荷載分配，利用改進折半法實現車輪荷載快速加載. 借助彈簧-質量模型通過簡支梁的數值算例對所建立分析系統的準確性進行了初步驗證，根據特定測試工況下的實橋響應對所建立分析系統的準確性作了進一步驗證，并對分析過程中的迭代進程、分析耗時等問題與傳統分析方法進行了對比，得到以下結論：

1）數值算例驗證結果顯示，基于所建立的分析系統所得到的分析結果與經典數值分析結果基本一致，初步說明引入等參映射及改進折半法建立公路車橋耦合分析系統的可行性.

2）四渡河大橋2個測試工況實測與仿真結果對比顯示，20 km/h和50 km/h車速下跨中應變峰值誤差分別為1.3%和0.31%. 所建立車橋耦合分析系統收斂速度較快，且得到的分析結果能夠與實測結果良好地吻合，進一步驗證了所建立的公路車橋耦合分析系統的準確性.

3）依托工程實例將所提出的分析方法與傳統分析方法進行比較，分析結果顯示本文所提出方法相比傳統方法計算結果基本保持一致，計算耗時明顯減少，具有較高的計算效率，對后續高強度高隨機車流下的公路車橋耦合分析具有很好的應用價值.

參考文獻

[1]? ? 謝青，韓萬水，劉修平，等. 基于模型修正的實體車-橋耦合分析系統建立及驗證[J]. 中國公路學報，2018，31（7）：126—136.

XIE Q，HAN W S，LIU X P，et al. Development and validation of solid vehicle-bridge interaction analysis system based on model updating [J]. China Journal of Highway and Transport，2018，31（7）：126—136. （In Chinese）

[2]? ? 殷新鋒，鄧露. 隨機車流作用下橋梁沖擊系數分析[J]. 湖南大學學報（自然科學版），2015，42（9）：68—75.

YIN X F，DENG L. Impact factor analysis of bridges under random traffic loads [J]. Journal of Hunan University （Natural Sciences），2015，42（9）：68—75. （In Chinese）

[3]? ? YU Y，DENG L，WANG W，et al. Local impact analysis for deck slabs of prestressed concrete box-girder bridges subject to vehicle loading[J]. Journal of Vibration and Control，2017，23（1）：31—45.

[4]? ? YU Y，CAI C S，DENG L. Vehicle axle identification using wavelet analysis of bridge global responses[J]. Journal of Vibration and Control，2017，23（17）：2830—2840.

[5]? ? 夏禾，張楠，郭薇薇，等. 車橋耦合振動工程[M]. 北京：科學出版社，2014：30—32.

XIA H，ZHANG N，GUO W W，et al. Coupling vibrations of train-bridge system [M]. Beijing：Science Press，2014：30—32. （In Chinese）

[6]? ? 桂水榮，陳水生，趙輝，等. 基于LS-DYNA公路橋梁車橋耦合振動模型[J]. 公路交通科技，2013，30（7）：40—45.

GUI S R，CHEN S S，ZHAO H，et al. Model of highway bridge subjected to vehicle-bridge coupling vibration based on LS-DYNA [J]. Journal of Highway and Transportation Research and Development，2013，30（7）：40—45. （In Chinese）

[7]? ? 韓萬水. 風-汽車-橋梁系統空間耦合振動研究[D]. 上海：同濟大學土木工程學院，2006：71—75.

HAN W S. Three-dimensional coupling vibration of wind-vehicle-bridge system [D]. Shanghai：College of Civil Engineering，Tongji University，2006：71—75. （In Chinese）

[8]? ? 李永樂. 風-車-橋系統非線性空間耦合振動研究[D]. 成都：西南交通大學土木工程學院，2003：95—98.

LI Y L. Nonlinear three-dimensional coupling vibration of wind-vehicle-bridge system [D]. Chengdu：School of Civil Engineering，Southwest Jiaotong University，2003：95—98. （In Chinese）

[9]? ? CAI C S，CHEN S R.? Framework of vehicle-bridge-wind dynamic analysis [J]. Journal of Wind Engineering and Industrial Aerodynamics，2004，92（7）：579—607.

[10]? 施穎，田清勇，宋一凡，等. 基于ANSYS的公路橋梁車橋耦合振動響應數值分析方法[J]. 公路，2010（3）：66—70.

SHI Y，TIAN Q Y，SONG Y F，et al. Numerical analysis method for vehicle bridge coupling vibration response of highway bridge based on ANSYS [J]. Highway，2010（3）：66—70. （In Chinese）

[11]? NGUYEN K，FREYTAG B，RALBOVSKY M. Assessment of serviceability limit state of vibrations in the UHPFRC-Wild bridge through an updated FEM using vehicle-bridge interaction [J]. Computers & Structures，2015，156：29—41.

[12]? 韓萬水，陳艾榮. 隨機車流下的風-汽車-橋梁系統空間耦合振動研究[J]. 土木工程學報，2008，41（9）：97—102.

HAN W S，CHEN A R. Three-dimensional coupling vibration of wind-vehicle-bridge systems under random traffic flow [J]. China Civil Engineering Journal，2008，41（9）：97—102. （In Chinese）

[13]? 朱志輝，徐智偉，程玉瑩，等. 基于精細有限元法的車致大跨度斜拉橋整體及局部振動研究[J]. 湖南大學學報（自然科學版），2018，45（1）：9—18.

ZHU Z H，XU Z W，CHENG Y Y，et al. Research on global and local vibration of long-span cable-stayed bridge induced by passing train based on fine finite element method [J]. Journal of Hunan University （Natural Sciences），2018，45（1）：9—18. （In Chinese）

[14]? 李小珍，張黎明，張潔. 公路橋梁與車輛耦合振動研究現狀與發展趨勢[J]. 工程力學，2008，25（3）：230—240.

LI X Z，ZHANG L M，ZHANG J. State of the art review and trend of studies on coupling vibration for vehicle and highway bridge system [J]. Engineering Mechanics，2008，25（3）：230—240. （In Chinese）

[15]? ZOU Q，DENG L，GUO T，et al. Comparative study of different numerical models for vehicle-bridge interaction analysis [J]. International Journal of Structural Stability and Dynamics，2016，16（9）：1636—1643.

[16]? 陳代海，李整，劉瓊，等. 公路橋梁2種車橋耦合振動分析方法的對比研究[J]. 鐵道科學與工程學報，2017，14（7）：1449—1456.

CHEN D H，LI Z，LIU Q，et al. Comparative research on two analysis methods for vehicle-bridge coupling vibration of highway bridges [J]. Journal of Railway Science and Engineering，2017，14（7）：1449—1456. （In Chinese）

[17]? 朱志輝，王力東，龔威，等. 基于改進迭代模型的車-橋耦合系統豎向隨機振動研究[J]. 湖南大學學報（自然科學版），2016，43（11）：120—130.

ZHU Z H，WANG L D，GONG W，et al. Study on vertical random vibration of train-bridge coupled system based on improved iteration model [J]. Journal of Hunan University （Natural Sciences），2016，43（11）：120—130. （In Chinese）

[18]? 張楠，夏禾. 基于全過程迭代的車橋耦合動力系統分析方法[J]. 中國鐵道科學，2013，34（5）：32—38.

ZHANG N，XIA H. A vehicle-bridge interaction dynamic system analysis method based on inter-system iteration [J]. China Railway Science，2013，34（5）：32—38. （In Chinese）

[19]? 李巖，吳志文，蔡明，等. 一種隨機車流與橋梁耦合振動的分析方法[J]. 哈爾濱工業大學學報，2018，50（3）：52—58.

LI Y，WU Z W，CAI M，et al. An analysis method for coupled vibration random traffic flow and bridge [J]. Journal of Harbin Institute of Technology，2018，50（3）：52—58. （In Chinese）

[20]? CHEN S R，WU J. Dynamic performance simulation of long-span bridge under combined loads of stochastic traffic and wind [J]. Journal of Bridge Engineering，2010，15（3）：219—230.

[21]? 韓萬水，馬麟，汪炳，等. 隨機車流-橋梁系統耦合振動精細化分析與動態可視化[J]. 中國公路學報，2013，26（4）：78—87.

HAN W S，MA L，WANG B，et al. Refinement analysis and dynamic visualization of traffic-bridge coupling vibration system [J]. China Journal of Highway and Transport，2013，26（4）：78—87. （In Chinese）

[22]? 王濤. 高速公路橋梁交通荷載調查分析及仿真模擬[D]. 西安：長安大學公路學院，2010：22—25.

WANG T. Investigation statistics and simulation for random traffic loading of expressway bridge [D]. Xian：School of Highway，Changan University，2010：22—25. （In Chinese）

[23]? 院素靜. 公路車-橋耦合典型車輛運動方程的建立及軟件設計[D]. 西安：長安大學公路學院，2012：9—13.

YUAN S J. Development and programing of typical vehicles equation of motion for coupling vibration between highway bridge and vehicles [D]. Xian：School of Highway，Changan University，2012：9—13. （In Chinese）

[24]? 易曉山，任鈞國，周建平. 一種精確積分的四邊形四結點等參單元[J]. 國防科技大學學報，1998，20（1）：1—4.

YI X S，REN J G，ZHOU J P. An accurately integrated 4-node quadrilateral element [J]. Journal of National University of Defense Technology，1998，20（1）：1—4. （In Chinese）

[25]? 張德豐. MATLAB數學實驗與建模[M]. 北京：清華大學出版社，2014：264—269.

ZHANG D F. MATLAB mathematical experiment and modeling [M]. Beijing：Tsinghua University Press，2014：264—269. （In Chinese）

[26]? BOWE C J，MULLARKEY T P. Wheel-rail contact elements incorporating irregularities [J]. Advances in Engineering Software，2005，36（11）：827—837.

[27]? 楊建榮，李建中，范立礎. 基于ANSYS的車橋耦合振動分析[J]. 計算機輔助工程，2007，16（4）：23—26.

YANG J R，LI J Z，FAN L C. Analysis on vehicle-bridge coupling vibration based on ANSYS [J]. Computer Aided Engineering，2007，16（4）：23—26. （In Chinese）

[28]? 汪炳. 雙向多車道隨機車流作用下大跨鋼桁梁懸索橋空間動力行為研究[D]. 西安：長安大學公路學院，2011：30—36.

WANG B. Spatial dynamic behavior of long-span steel truss girder suspension bridge under two-way multi-lane stochastic traffic flow [D]. Xian：School of Highway，Changan University，2011：30—36. （In Chinese）

[29]? 楊果岳. 車輛隨機荷載與柔性路面相互作用的研究[D]. 長沙：中南大學土木建筑學院，2007：19—22.

YANG G Y. Study on the interaction of vehicle random loads and flexible pavement [D]. Changsha：School of Civil Engineering，Central South University，2007：19—22. （In Chinese）

[30]? ISO 8608：1995 Mechanical vibration—road surface profiles—reporting of measured data [S]. Geneva：International Standard Organization，1995：14—21.

[31]? 韓萬水. 重載交通動態過橋可視化仿真與安全評價[M]. 北京：人民交通出版社，2016：64—65.

HAN W S. Visual simulation and safety evaluation of heavy traffic dynamic bridge [M]. Beijing：China Communication Press，2016：64—65. （In Chinese）