非線性橢圓方程變分方法研究的若干新進展

云南師范大學數學學院

1 項目研究的背景和意義

Hilbert與變分法：1900年， 國際數學領袖、20世紀最偉大的數學家D.Hilbert在巴黎國際數學家大會上， 提出的23個著名數學問題中有3個問題與變分法直接相關， 特別是第23個問題就是 “變分法的進一步發展”，Hilbert認為變分法將匯入20世紀數學發展的主流。

希爾伯特(David Hilbert 1862-1943)

變分法的起源：18世紀著名數學家J.Bernoulli提出了最速降線問題：一個質點在重力作用下，從一個給定點A到不在它垂直下方的另一點B，如果不計摩擦力，問沿著什么曲線滑下所需時間最短?

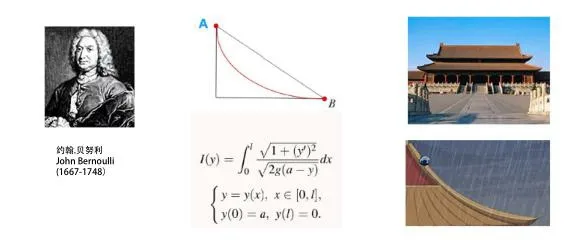
變分法的重要里程碑：1973年，意大利倫琴科學院院士A.Ambrosetti和美國科學院院士P.H.Rabinowitz提出了著名的山路定理， 標志著變分法有了重大發展。

變分法的近期發展：2018年，意大利數學家A.Figalli因在最優傳輸理論及其在偏微分方程等方面的應用做出的重要貢獻獲菲爾茲獎(Fields Medal， 這是數學界2個最重要獎項之一)。

A.Figalli

變分法中的2個典型困難：一是失去“緊性”；二是失去“光滑性”。

失去“緊性”的問題：最早在文[H.Brezis，L.Nirenberg，Positive solutions of nonlinear elliptic equations involving critical Sobolev exponents， Comm.Pure Appl.Math.36 (1983)437-477]中提出。

失去“緊性”的典型例子Brezis-Nirenberg 問題：有界區域上帶臨界指數的問題

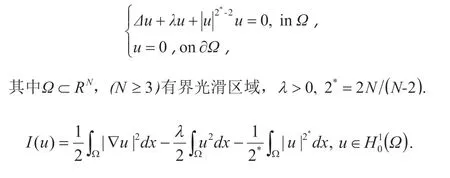
失去“光滑性”的問題：最早出現在文[S.Kurihara， Large-amplitude quasi-solitons in superfluids films， J.Phys.Soc.Jpn.50(1981)3262-3267]中提出的一類帶修正項的Schrodinger方程駐波的研究中.

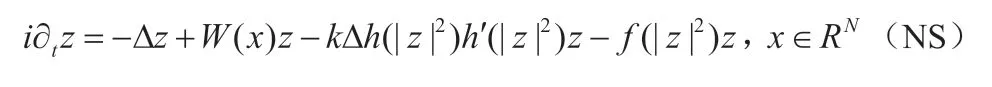
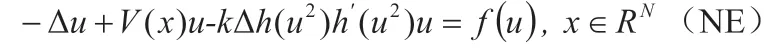
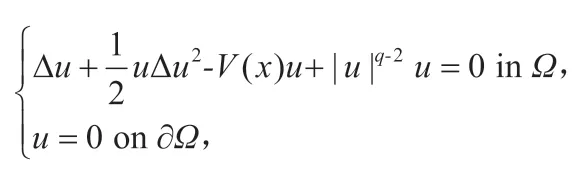
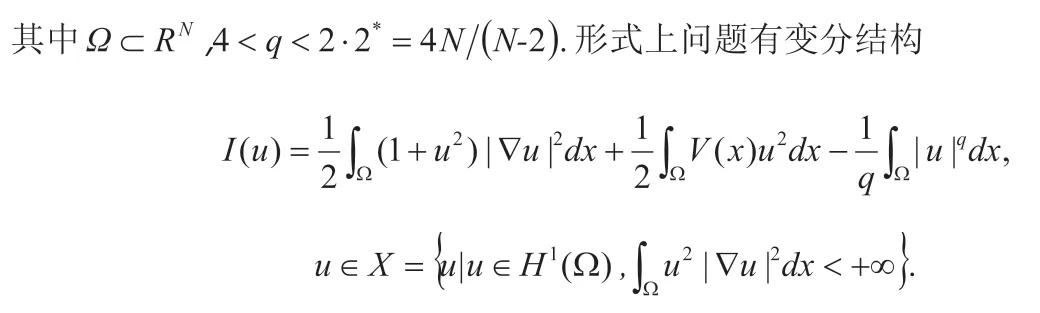
X不是一個線性空間，u，v屬于X，不一定屬于X，很難找到一個合適的空間， 使得I是光滑泛函，這導致很多經典的變分技巧不能直接用來研究該方程。

項目提出了變分泛函擾動法。變分泛函擾動法的主要思想：用光滑泛函逼近非光滑泛函。 考慮擾動泛函

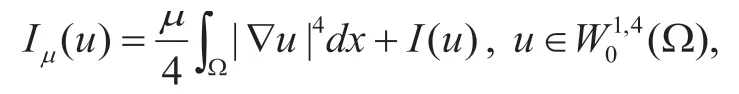
2 項目主要研究內容及發現點

1）提出了一種把非光滑變分問題轉化為標準變分問題的新方法——變分泛函擾動法。克服了約束極小化、Nehari流形和變量代換等方法不能研究一般擬線性橢圓方程的局限性。該方法具有原創性， 已成為研究具有重要物理背景的帶修正項的Schr?dinger 方程解存在性的1種重要方法。

2）對擾動方法做了進一步的討論， 通過添加2項擾動來獲得擬線性橢圓方程變號解的存在性。 特別將我們提出的新方法應用于幾類典型的擬線性橢圓方程：全空間上擬線性橢圓方程；帶參數形式擬線性橢圓方程；帶臨界指數擬線性橢圓方程.取得了突破性的進展。

3）項目還有其他幾個重要工作， 例如：全空間上非線性Schr?dinger方程組混合態解的存在性；漸近線性Schr?dinger方程變號解、半空間橢圓邊值問題、重調和方程及帶Hardy項的p-重調和方程變號解、哈密頓性橢圓方程組半經典問題基態解的集中現象等。

3 成果的收錄、引用及評價情況

該成果的70篇論文發表在Calc.Var.Partial Differential Equations， Comm.Partial Differential Equations， J.Differential Equations， Nonlinearity， Proc.Amer.Math.Soc.等該領域國際公認的權威期刊上，全部被SCI收錄， 其中JCR一區期刊上52篇。ESI高被引論文5篇， 其新方法、新思想及新結果被國內外同行在 Calc.Var.Partial Differential Equations，Comm.Partial Differential Equations，J.Differential Equations， Proc.Roy.Soc.Edinburgh Sect.， Z.Angew.Math.Phys.等 SCI刊物上總引697次， 他引510次；單篇SCI論文他引最高為67次； 20篇核心論文SCI他引383次；8篇代表性論文SCI他引192次。

所開展的系列工作被國際數學界最重要的評論機構“美國《數學評論》”收錄并摘評。例如：日本Kyoto Sangyo University， W.Tatsuya 教授在美國《數學評論》評論代表性論文[1]：“In this paper，the authors propose a newapproach…Their approach is effective for dealing with multiple solutions of quasilinear equations in a general form to which the idea of change of variables does not apply (在該文中，作者提出了一種新方法，克服了變量代換方法不能研究一般擬線性橢圓方程的局限性，并用該方法獲得了其無窮多解的存在性)”美國St.John’s University，F.Catrina教授在美國《數學評論》評論代表性論文[3]：“The authors use a perturbation method to prove the existence of ground state solutions to modified nonlinear Schr"odinger equations.The existence of solutions is proved first for a perturbed problem with additional terms， and with constant(作者利用擾動方法證明了帶修正項的擬線性Schr?dinger方程基態解的存在性，這是該方程在臨界情形下解存在性的第一個結果)”。

項目提出的新方法、新思想及獲得的新結果被美國、 意大利、日本、巴西、突尼斯、越南、波蘭以及國內同行在該領域國際公認的權威期刊上多次介紹和引用。國內也有很多同行對我們的工作給予了高度評價。

4 促進科學發展的重要意義

1）發展了變分法，針對失去“光滑性”的問題，原創性地提出一種把非光滑變分問題轉化為光滑變分問題的新方法——變分泛函擾動法， 完全克服了約束極小化、Nehari流形和變量代換等方法不能研究一般擬線性橢圓方程的局限性，該方法已成為研究擬線性橢圓方程特別是有重要物理意義的帶修正項的Schr?dinger方程解存在性的主要方法之一(見代表性論文[1])。

2）應用所提出的新方法在擬線性橢圓方程解的存在性、多重性及解的性態分析等問題取得了突破性進展(見代表性論文[2，3，6，7])。

3）發現了全空間及半空間上p-Laplace算子第二特征值及其等價定義，刻畫了該算子的特征值序列并完整描繪了相應的特征曲線圖，結合團隊所發展的Cerami條件下的變號臨界點定理，進而在全空間及半空間上帶位勢井的漸近線性p-Laplace方程變號解存在性方面獲得系列全新結果；在高階Sobolev空間中提出了1種新的產生流不變集的算子，得到了重調和方程及帶Hardy項的p-重調和方程變號解的存在性(見代表性論文[4，5，8])。

4）代表性文獻

[1]Xiangqing Liu，Jiaquan Liu， Zhiqiang Wang.Quasilinear elliptic equations via perturbation method.Proc.Amer.Math.Soc.141(1) (2013) 253-263.

[2]Xiangqing Liu， Jiaquan Liu， Zhiqiang Wang.Quasilinear elliptic equations with criticalgrowth via perturbation method.J.Differential Equations 254(2013) 102-124.

[3]Xiangqing Liu， Jiaquan Liu， Zhiqiang Wang.Ground states for quasilinear Schr?dinger equations with critical growth.Calc.Var.Partial Differential Equations 46 (2013)641-669.

[4]Xiangqing Liu， Yisheng Huang.On signchanging solution for a fourth-order asymptotically linear elliptic problem.Nonlinear Anal.72 (2010)2271-2276.

[5]Xiangqing Liu， Jiaquan Liu.On a boundary value problem in the half-space.J.Differential Equations 250 (2011) 2099-2142.

[6]Xian Wu.Multiple solutions for quasilinear Schr?dinger equations with a parameter.J.Differential Equations 256(7) (2014) 2619-2632.

[7]Xian Wu， Ke Wu.Existence of positive solutions， negative solutions and high energy solutions for quasilinear elliptic equations on RN.Nonlinear Anal.Real World Appl.16(2014)48-64.

[8]Yanheng Ding， Cheng Lee， Fukun Zhao*.Semiclassical limits of ground state solutions to Schr?dinger systems.Calc.Var.Partial Differential Equations 51(2014) 725-760.