2020年高考數(shù)學江蘇卷第20題的反思與推廣
錢月鳳 (江蘇省蘇州中學校 215007)
解題是一門實踐性的學問,研究解題是為了提高解題能力.本文從2020年江蘇高考數(shù)學第20題出發(fā),從解題反思的視角,反思了其解題思路、問題表征和思想策略,之后對此高考題進行改編與推廣,最后總結(jié)了筆者的幾點想法.
1 案例呈現(xiàn)
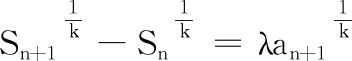
(1)若等差數(shù)列{an}是“λ~1”數(shù)列,求λ的值;
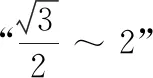
(3)對于給定的λ,是否存在三個不同的數(shù)列{an}為“λ~3”數(shù)列,且an≥0?若存在,求λ的取值范圍;若不存在,說明理由.
解(1)(2)略.
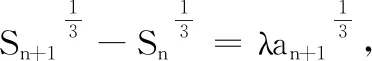
①若λ≤0或λ=1時,則關(guān)于cn的方程(*)只有一解cn=1,則符合條件的數(shù)列{an}只有一個,此數(shù)列為1, 0, 0, 0, ….
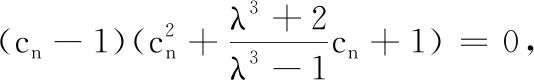
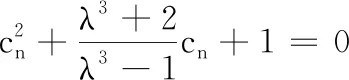
由于數(shù)列{Sn}從任何一項求其后一項均有兩種不同的結(jié)果,所以這樣的數(shù)列{Sn}就有無數(shù)多個,則對應(yīng)的{an}也有無數(shù)多個.
綜上所述,當0<λ<1時,存在三個不同的各項非負的數(shù)列{an}為“λ~3”數(shù)列;當λ≤0或λ≥1時,不存在三個不同的各項非負的數(shù)列{an}為“λ~3”數(shù)列.
2 解題反思
由于例1第(1)問難度不大,第(2)問與第(3)問的解題思想與方法有共通之處,故將分析的重點放在第(3)問,主要從解題思路、問題表征以及思想策略三方面對解題過程進行反思.
2.1 反思解題結(jié)構(gòu),實現(xiàn)解題思路明晰化
提煉第(3)問的解題步驟,大致可以分為三大步,記作L1,L2和L3.
第一大步L1:根據(jù)“λ~3”數(shù)列的定義,將問題轉(zhuǎn)化為方程根的問題.有這樣的一個信息流程圖(圖1).
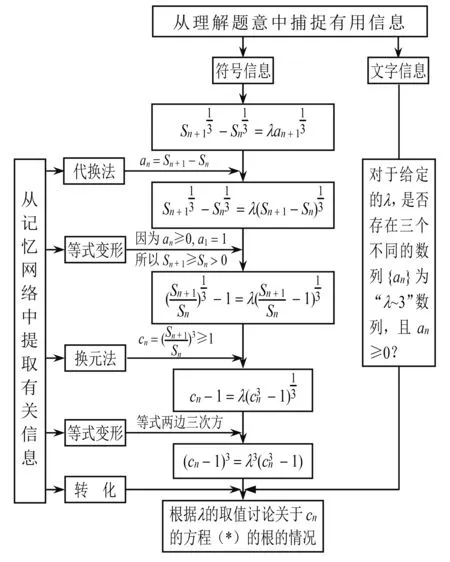
圖1 信息流程圖
第二大步L2:根據(jù)λ的取值來討論關(guān)于cn的方程(*)的根的情況,可分為三類:①λ≤0或λ=1時,方程(*)只有一解cn=1;②λ>1時,方程(*)只有一解cn=1;③0<λ<1時,方程(*)有兩個解:一解為1,另一解大于1.
第三大步L3:根據(jù)方程(*)根的情況分析數(shù)列{Sn}的個數(shù),進而判斷滿足條件的數(shù)列{an}的個數(shù).當λ≤0或λ≥1時,方程(*)只有一解,則符合條件的數(shù)列{an}只有一個;當0<λ<1時,數(shù)列{Sn}就有無數(shù)多個,則對應(yīng)的{an}也有無數(shù)多個,故此時存在三個不同的各項非負的數(shù)列{an}為“λ~3”數(shù)列.
將整個解題過程分為以上三大步,使復(fù)雜問題的求解過程得以清晰地呈現(xiàn).由以上三大步的結(jié)構(gòu)分析中可以看到,最關(guān)鍵的是第一大步,而第一大步中最有價值的解題進展是“利用換元法將原始問題轉(zhuǎn)化為討論方程根的情況問題”.
2.2 反思問題表征,力求解題過程自然化
問題表征是解決問題時理解問題的方式.反思問題表征,能加強對問題信息的感知、理解與內(nèi)化,促進解題主體對解題思路的探求.
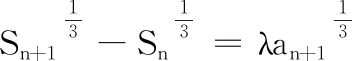
問題的呈現(xiàn)方式對策略選擇有直接的影響.若問題呈現(xiàn)時省略第(2)問直接跳到第(3)問,很多考生會產(chǎn)生無從下手之感.第(2)問給出后,解題主體會嘗試從基礎(chǔ)入手,不斷探索解題思路,由淺入深,逐漸找到第(3)問的解題突破口,這樣便能自然地往下想、往下做.單墫老師曾在《解題研究》一書中提到,所謂自然,即抓住問題的實質(zhì),題目該怎么解就怎么解,不顧弄玄虛,樸實自然[1].
2.3 反思思想策略,促使數(shù)學思維深刻化
例1第(3)問所選擇的主要解題策略是簡化與轉(zhuǎn)化,涉及的主要知識點、數(shù)學方法、數(shù)學思想和數(shù)學能力如表1所示.

表1 例1第(3)問涉及的知識點、 數(shù)學方法、數(shù)學思想和數(shù)學能力
問題涉及的數(shù)學知識點不多,但要真正解決該問題,需要解題主體擁有良好的數(shù)學思維品質(zhì).能否透過問題表面洞察其本質(zhì),是數(shù)學思維深刻與否的主要表現(xiàn);全面周密地思考問題,是數(shù)學思維嚴謹性的主要特征.當然,解決該問題還需解題者具備靈活的思維,善于調(diào)整解題思路與方法,隨機應(yīng)變.當考生面對問題不知從何下手時,可以靜下來想一想:解題的突破口在哪?問題中最重要的條件是哪一個或哪幾個?既然我找到了我認為最重要的條件,我該怎么使用它?它想告訴我什么?隱藏在它背后的深刻含義是什么?一旦解題者在思考與探索中找到了突破口,便能選擇合適的解題策略,靈活地將基本數(shù)學思想與方法運用其中,自然地將陌生難題轉(zhuǎn)化為熟悉的問題.
3 拓展延伸
筆者結(jié)合現(xiàn)有經(jīng)驗,對例1進行了更加深入的研究.我們可以將例1中k為大于1的正整數(shù)時的所有情形考慮清楚(見例2).
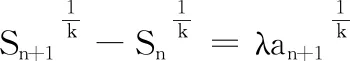
(1)對于給定的λ和k(k為大于等于3的奇數(shù)),是否存在三個不同的數(shù)列{an}為“λ~k”數(shù)列,且an≥0?若存在,求λ的取值范圍;若不存在,說明理由.
(2)對于給定的λ和k(k為正偶數(shù)),是否存在三個不同的數(shù)列{an}為“λ~k”數(shù)列,且an≥0?若存在,求λ的取值范圍;若不存在,說明理由.
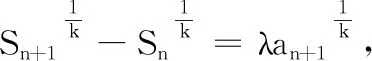
(1)①若λ≤0時,因為k為大于等于3的奇數(shù),所以λk≤0,則關(guān)于dn的方程(*)只有一解dn=1,即符合條件的數(shù)列{an}只有一個,此數(shù)列為1, 0, 0, 0, ….
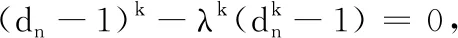
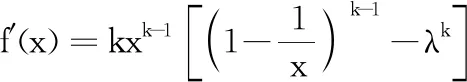
由于數(shù)列{Sn}從任何一項求其后一項均有兩種不同的結(jié)果,所以這樣的數(shù)列{Sn}就有無數(shù)多個,則對應(yīng)的{an}也有無數(shù)多個.
綜上所述,當0<λ<1時,存在三個不同的各項非負的數(shù)列{an}為“λ~k”數(shù)列;當λ≤0或λ≥1時,不存在三個不同的各項非負的數(shù)列{an}為“λ~k”數(shù)列.
(2)①若λ=0,則關(guān)于dn的方程(*)只有一解dn=1,即符合條件的數(shù)列{an}只有一個,此數(shù)列為1, 0, 0, 0, ….
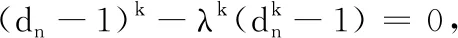
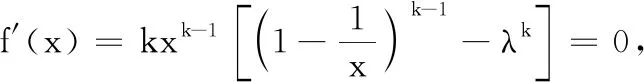
由于數(shù)列{Sn}從任何一項求其后一項均有兩種不同的結(jié)果,所以這樣的數(shù)列{Sn}就有無數(shù)多個,則對應(yīng)的{an}也有無數(shù)多個.
綜上所述,當0<λ<1或-1<λ<0時,存在三個不同的各項非負的數(shù)列{an}為“λ~k”數(shù)列;當λ=0或λ≥1或λ≤-1時,不存在三個不同的各項非負的數(shù)列{an}為“λ~k”數(shù)列.
現(xiàn)將例2進一步推廣,改編成例3;例3具體問題及其求解分析如下:
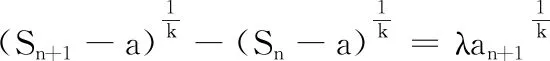
(1)對于給定的a,λ和k(k為大于等于3的奇數(shù)),是否存在三個不同的數(shù)列{an}為“a~λ~k”數(shù)列,且an≥0?若存在,求λ的取值范圍;若不存在,說明理由.
(2)對于給定的a,λ和k(k為正偶數(shù)),是否存在三個不同的數(shù)列{an}為“a~λ~k”數(shù)列,且an≥0?若存在,求λ的取值范圍;若不存在,說明理由.
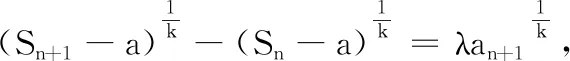
于是,問題轉(zhuǎn)化為根據(jù)λ的取值討論方程(*)的根的問題.之后的求解與例2相同.
答案 (1)當0<λ<1時,存在三個不同的各項非負的數(shù)列{an}為“a~λ~k”數(shù)列;(2)當0<λ<1或 -1<λ<0時,存在三個不同的各項非負的數(shù)列{an}為“a~λ~k”數(shù)列.
例3還可進一步推廣改編成例4,例4具體問題及其求解分析如下:
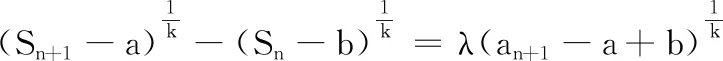
(1)對于給定的a,b,λ和k(k為大于等于3的奇數(shù)),是否存在三個不同的數(shù)列{an}為“a~b~λ~k”數(shù)列,且an≥|a-b|?若存在,求λ的取值范圍;若不存在,說明理由.
(2)對于給定的a,b,λ和k(k為正偶數(shù)),是否存在三個不同的數(shù)列{an}為“a~b~λ~k”數(shù)列,且an≥|a-b|?若存在,求λ的取值范圍;若不存在,說明理由.
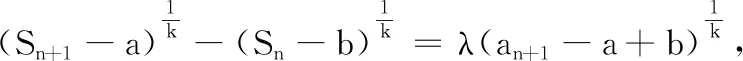
于是,問題轉(zhuǎn)化為根據(jù)λ的取值討論方程(*)的根的問題.之后的求解與例2相同.
答案 (1)當0<λ<1時,存在三個不同的各項非負的數(shù)列{an}為“a~b~λ~k”數(shù)列;(2)當0<λ<1或-1<λ<0時,存在三個不同的各項非負的數(shù)列{an}為“a~b~λ~k”數(shù)列.
特別說明的是,例2~例4中k=1時的情形比較簡單,而k是分數(shù)或無理數(shù)時的情況又較為復(fù)雜,故以上三題只研究k為大于等于2的正整數(shù)時的情形.
4 反思總結(jié)
通過解題反思,結(jié)合自身經(jīng)驗關(guān)于解題總結(jié)了以下幾點想法:(1)深刻理解題意后,努力尋找解題突破口;(2)掌握基本數(shù)學思想與方法,化繁為簡,化難為易;(3)大膽探索,跟著直覺往下想、往下做;(4)不斷思考,努力產(chǎn)生“新想法”和“新途徑”;(5)全面思考問題,創(chuàng)造性地克難攻堅.

