基于凸優化的再入軌跡三維剖面規劃方法
周祥,張洪波,*,何睿智,湯國建,包為民
1. 國防科技大學 空天科學學院,長沙 410073 2. 中國航天科技集團有限公司科技委,北京 100048
可重復使用飛行器能夠實現天地間的多次往返,從空間再入大氣層后,依靠大升阻比氣動外形實現在臨近空間的遠距離滑翔飛行,從而抵達預定目標[1]。再入滑翔段軌跡規劃的準確性和快速性對于改善該類飛行器的制導效果具有重要意義。
為了降低軌跡規劃的計算量,以航天飛機軌道器為代表的可重復使用飛行器采用固定攻角剖面,以傾側角為唯一控制量的方式進行軌跡規劃,進而實現制導任務。這種基于二維剖面的規劃方法具有計算負擔小、方法簡單、容易實現等優點,在航天飛機等飛行器上得到了成功應用。然而,這種計算量小的規劃方法難以充分發揮可重復使用飛行器的大范圍機動能力。飛行器固有的機動能力主要由飛行器的總體布局和氣動性能決定,上述因素確定后,如何選擇合適的控制策略從而充分發揮出其固有的機動能力就顯得尤為重要。1998年,文獻[2]提出如果將傳統二維剖面規劃方法中固定攻角的條件放開,同時采用攻角和傾側角作為控制量,將有助于充分發揮飛行器的機動能力。文獻[3]將同時考慮攻角和傾側角作為控制量的軌跡規劃問題描述為三維剖面規劃問題,使用阻力加速度和側向加速度作為中間控制變量(即剖面設計量),引入降階動力學系統降低問題求解的計算量,這里的三維剖面從控制量的角度講即是對攻角和傾側角變化規律的一種表征,而傳統的二維剖面規劃方法只能獲得對傾側角變化規律的表征。文獻[4]在加速度剖面規劃中同時考慮縱向和側向運動,首先基于二維剖面規劃一條可行軌跡,其次基于三維剖面獲得最優軌跡。文獻[5]提出了一種分層策略的三維剖面規劃方法,該方法采用側向降階運動模型對縱向、側向剖面進行反復迭代,直至滿足終端縱程和橫程要求。文獻[6]將基于分層策略的三維剖面規劃方法應用到再入覆蓋區求解中,獲得了相比基于二維剖面規劃方法更大的覆蓋區,驗證了機動能力得到充分發揮后的效果。整體來看,目前對二維剖面規劃方法的研究較多[7-9],而關于三維剖面規劃方法的研究還比較少,還有很多技術問題有待解決,其中,計算效率是限制三維剖面規劃技術的主要瓶頸之一。
近年來,內點法的快速發展使得凸優化在求解效率方面相比傳統方法如偽譜法的優勢愈發明顯[10-11]。除此之外,凸優化問題的局部極小點就是全局最小點,這一良好的理論性質也為該方法的廣泛應用奠定了基礎[12]。由于實際中大量的優化問題都是非凸的,如何將軌跡規劃等這類具有多種約束的原始非凸問題轉化為凸問題是應用凸優化方法的關鍵,包括對非線性動力學、過程約束、控制量約束、優化目標的凸化。截止目前,凸優化已經在再入軌跡規劃、行星著陸、無人機路徑規劃等方面得到了應用,一系列凸化方法被廣泛使用在這些問題中,包括約束松弛和連續線性化等技術[13]。凸優化早期在航天中的應用主要是解決動力下降段的軌跡規劃問題,在這類問題的凸化過程中提出了無損凸化的概念[14-15]。
文獻[16]利用序列凸優化的方法求解再入軌跡規劃問題,相比偽譜法顯示出了很好的求解效率,文中所提的序列凸化方法是目前處理強非線性動力學約束與非線性過程約束的主要方法。文獻[17]中討論了利用序列凸優化求解再入軌跡規劃問題的收斂性問題,序列凸優化的收斂性與解的等價性緊密相關。文獻[18]實現了基于凸優化在線軌跡規劃的閉環跟蹤制導,將軌跡規劃子問題和軌跡跟蹤制導指令求解子問題均轉化為凸問題,從而可實現在線快速求解,取得了很好的制導效果。文獻[19-21]對于改進序列凸優化方法的性能提供了多種技巧。文獻[22]利用凸優化求解再入軌跡規劃問題時將攻角與傾側角同時作為控制量,通過定義中間變量實現了對控制量約束的凸化處理。但并未給出規劃后的指令計算方法,限制了該方法在實際問題中的應用。
總體來看,目前基于三維剖面的再入軌跡規劃方法研究還比較少,主要存在的問題包括:① 動 力學模型簡化較多,導致問題求解精度較低;② 為了減低計算量,將加速度剖面進行簡單參數化,人為限制了剖面求解的搜索空間,不利于充分發揮飛行器的能力。總的來看,已有三維剖面規劃方法并未很好解決軌跡規劃的求解精度與計算效率之間的矛盾。
基于上述分析,本文采用完整動力學模型,利用凸優化方法求解再入三維剖面規劃問題。主要貢獻是:① 將原始三維剖面規劃問題描述為最優控制問題,采用合適的凸化技巧將考慮多種約束條件的原問題轉化為凸優化問題,包括動力學約束、路徑約束和控制量約束的凸化,其次對連續凸問題進行離散化;② 引入指令反解步驟,通過優化后的中間控制量計算攻角和傾側角指令,并建立了相應的序列迭代算法,通過迭代求解凸優化子問題,從而獲得原問題的可行解。通過數值仿真證明了本文方法的可行性和收斂性。
本文的框架結構:引言部分介紹研究背景和研究現狀;第1部分介紹問題描述;第2部分介紹如何對原問題進行凸化與離散處理,將其轉化為一個凸的數學規劃問題;第3部分介紹如何利用凸優化的解(即中間變量和狀態量)反解攻角和傾側角指令,并給出了序列凸化算法的步驟;第4部分進行了數值仿真;第5部分給出了結論。
1 問題描述
1.1 三維剖面規劃問題
首先建立軌跡規劃中使用的動力學模型。在建模過程中主要引入以下假設: ① 考慮地球自轉;② 僅考慮球形引力;③ 認為地球外形是一個標準圓球。可重復使用飛行器在再入過程中進行無動力飛行,由于大氣阻力的作用,飛行器能量是單調遞減的,為了降低優化變量的數目,本文采用能量E作為自變量,定義為
E=V2/2-μ/r
(1)
式中:μ為地球引力常數;r為地心距;V為速度。
進而得到以能量為自變量的再入質心動力學模型為
(2)
式中:λ為經度;φ為緯度;θ為當地速度傾角;σ為航跡偏航角;L、D分別為升力和阻力加速度;υ為傾側角;由地球自轉引起的哥氏加速度項Cθ和Cσ以及牽連加速度項C′θ和C′σ可分別表示為
(3)
上述所有變量均可采用如下歸一化方法進行無量綱化處理。
(4)
(5)
式中:R0為地球平均半徑;g0為R0處的引力;ωe為地球旋轉角速度。升力和阻力加速度的定義為
(6)
式中:Mr為飛行器質量;Sr為參考面積;CL、CD分別為升力系數和阻力系數,通常為攻角α和馬赫數Ma的函數;ρ為大氣密度,有
ρ=ρ0e-β h
(7)
其中:β=1/hs,hs=7 110 m;ρ0=1.225 kg/m3,h為高度。如無特殊說明,下文所有變量均為無量綱化處理后的值。
以E為自變量的動力學方程包括5個狀態參數和2個控制指令。前者指地心距r、經度λ、地心緯度φ、當地速度傾角θ和航跡偏航角σ,而速度與自變量有關,可以通過式(8)確定
(8)
將獨立描述飛行器運動狀態的參數構成狀態矢量x,可表示為
x=[r,λ,φ,θ,σ]T
(9)
2個控制指令是攻角和傾側角,利用它們實現對氣動力大小和方向的控制,所以再入軌跡規劃中的控制矢量U′可表示為
U′=[α,υ]T
(10)
在軌跡規劃中需要對控制指令的幅值進行約束,可以表示為
αmin≤α≤αmax
(11)
υmin≤|υ|≤υmax
(12)
式中:|·|表示絕對值,υmax>υmin≥0。
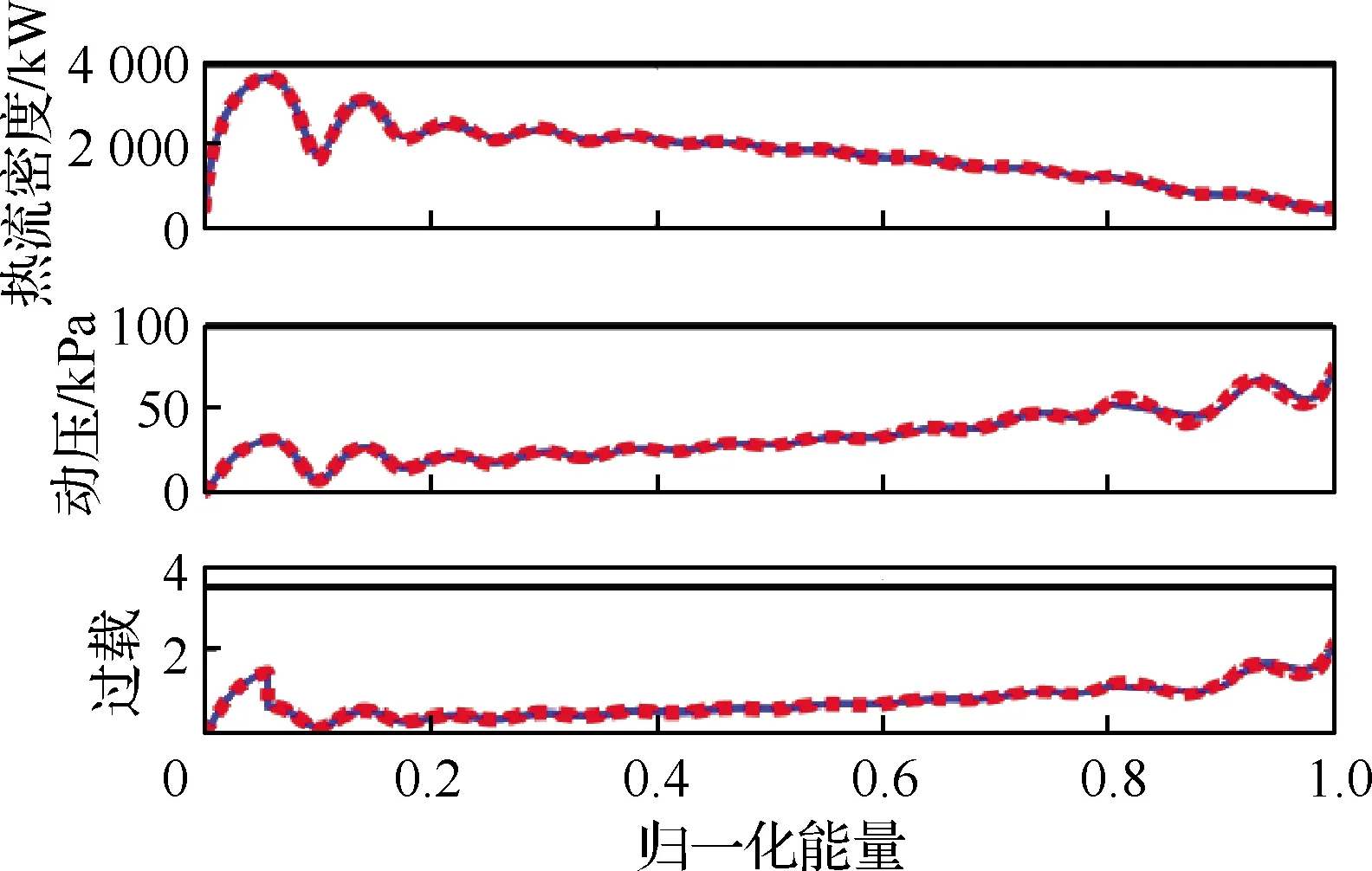
過程約束主要有:熱流密度、動壓、法向過載和氣動力,前3個約束用于避免飛行器結構受到破壞,第4個約束用于確保飛行器有足夠氣動力用于軌跡控制,分別表示為
(13)
(14)
(15)
(16)
軌跡規劃的邊界條件包括初始狀態約束和終端狀態約束,表示為
(17)
式中:x0和xf由具體任務給定;E0、Ef分別為初始狀態和終端狀態對應的能量。
優化目標可以表示為一般形式

(18)
式中:Φ(·)為終端目標函數;L(·)為過程目標函數。
至此,將再入軌跡三維剖面規劃問題記為P0,表示如下
(19)
在問題P0中,動力學方程和過程約束均是非線性的,因此這是一個連續的非線性最優控制問題。同時,由于控制指令攻角并不顯含在方程式(2)中,這也增加了該問題的求解難度。
1.2 新控制量的選擇
再入軌跡三維剖面規劃問題的控制量是攻角和傾側角,但是,由于攻角在再入動力學方程式(2) 中是隱含的,攻角通過影響氣動系數從而改變氣動力,傾側角則通過與三角函數進行復合而顯含于式(2)中,因此,原動力學方程式(2)關于攻角和傾側角是強非線性的。由于凸優化問題中等式約束必須是線性的,若繼續使用攻角和傾側角作為軌跡規劃的控制量,則顯著增加了對原方程式(2) 進行線性化的難度,并且線性化后的動力學方程也容易引起再入軌跡的“抖振”現象[16]。
為了避免上述問題的出現,可以定義新控制量,從而獲得新的線性化方程。新控制量的選擇應滿足以下2個條件:① 新控制量可以比較方便地將動力學方程中與之相關的一項表示為關于它的線性表達式;② 新控制量與原始控制量之間應該存在唯一映射關系。因此,本文定義如下新的控制變量:
(20)

(21)
這里引入u3的意義在于建立u1和u2之間的關系,方便后續進行控制量約束的等價轉換。
定義了新的控制量后,式(2)所示的動力學方程可以重新寫為
(22)
令U=[u1,u2,u3]Τ,將式(22)簡寫為

(23)
式中:
(24)
(25)
(26)
在動力學方程式(23)中,新控制量矢量U關于矩陣G(x)是線性的;g(x)為關于狀態量的非線性項,但其中包含阻力加速度項D,這與原始控制量攻角有關,關于該問題對求解精度的影響將在數值仿真中進行分析;h(x)為與地球自轉相關的小量。
2 凸化與離散
2.1 凸 化
1)控制量約束的處理
定義了新控制量(u1,u2,u3)后,需將如式(11) 和式(12)所示的原始控制量約束轉化為對新控制量的約束。由于控制量u3僅與攻角和馬赫數有關,由參考軌跡對應的高度和速度可得到參考馬赫數Mar。基于攻角取值范圍Cα,采用一維優化方法線搜索確定控制量u3的取值范圍,表示為
(27)
(28)
式中:Cα=[>αmin,αmax],則攻角幅值約束可以轉化為控制量u3的幅值約束,表示為
(u3)min≤u3≤(u3)max
(29)
傾側角幅值約束可以轉化為對控制量u1的約束,表示為
u3cos(υmax)≤u1≤u3cos(υmin)
(30)
至此,實現了對控制量幅值約束的轉化處理,且轉化后的約束(29)和(30)均是凸的。
除了上述對控制量幅值約束進行轉化外,對式(21)所示的非凸附加約束也要進行凸化處理。這里采用松弛技術對其進行凸化[16],得到如下凸約束為
(31)
上述松弛過程的合理性證明將在后面進行介紹。
2) 動力學方程的線性化
動力學方程作為等式約束,在凸優化問題中必須是線性的。這里介紹如何對式(23)所示的動力學方程進行線性化處理。基于參考軌跡(x(k),α(k),υ(k)),其中上標k表示參考軌跡序號,由一階泰勒展開可得
(32)
將式(32)化簡為

(33)
其中:
(34)
B=G|x=x(k)
(35)
C=g(x(k))-Ax(k)+h(x(k))
(36)
根據推導,線性化矩陣A和B的表達式為
(37)
B(xk)=
(38)
其中:
(39)
(40)
(41)
(42)
為了降低線性化誤差,需添加信賴域約束,表示為
|x-x(k)|≤δ
(43)
式中:δ表示信賴域半徑,與x維數相同。
3) 過程約束的線性化
在式(13)~式(16)所示的4項過程約束中,對應函數均具有強非線性,且既不是凸函數也不是凹函數,因此仍需要對這些函數進行線性化。本文采用文獻[16]提出的處理方法,利用一階泰勒展開,將4項過程約束轉化為關于地心距的線性約束,統一記為
(44)
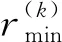
4) 目標函數的選擇
在凸優化問題中,目標函數必須是凸的或線性的。為了簡化處理,這里以終端位置誤差最小為主要指標。由于終端位置由經度和緯度共同描述,這也是一個終端性能指標,可以表示為
(45)

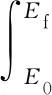
(46)
式中:C1和C2均為權重系數,用于平衡不同項之間的量級差異。
由于引入的附加項是線性的,因此式(46)所示的目標函數仍然是凸的。
基于上述凸化處理,可以得到具有凸目標函數、凸或線性約束的連續優化問題,記為問題P1,表示為
(47)
由于問題P1中優化目標是終端位置誤差最小,因此相應的終端約束應去除對經緯度的限制,將終端約束調整為
xf=[rf, ~, ~,θf,σf]Τ
(48)
式中:~表示該項無約束。從工程實現的角度考慮,在終端約束中對速度傾角和航跡偏航角施加了嚴格等式約束。
為了證明問題P1中松弛過程的合理性,這里引入如下2個假設:
假設1式(43)所示的信賴域約束|x-x(k)|≤δ在定義域的大部分區間內不會取到邊界,即除了少數有限個連接點外,在[>E0,Ef]上|x-x(k)|<δ是恒成立的。
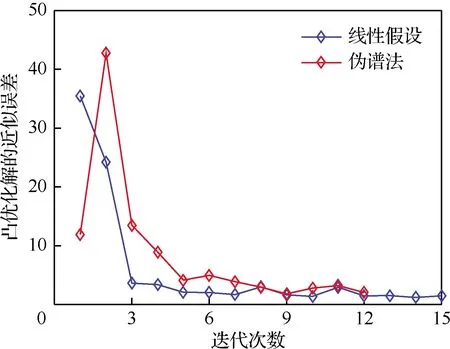
假設2式(44)所示的過程約束rmin≤r≤rmax在定義域的大部分區間內不會取到邊界,即除了少數有限個連接點外,在[>E0,Ef]上rmin 對于假設1,只要在求解過程中設置一個充分大的δ,即可保證在[>E0,Ef]上|x-x(k)|<δ是恒成立的。對于假設2,由于求解過程采用了梯度下降算法,當迭代解接近過程約束邊界時,控制量將迫使當前解遠離邊界,所以能夠保證在大部分連續定義域內rmin 問題P1是一個連續凸優化問題,其目標函數是凸的,約束是凸或線性的,但狀態量和控制量是連續的,這為直接求解該問題帶來了困難。因此,將其轉化為對有限參數進行尋優的數學規劃問題,應用數值方法進行求解是一種可行的方法。這里介紹對問題P1進行離散化,從而便于求解。 將自變量變化域[>E0,Ef]等間距離散為N個間隔,則自變量離散為E0,E1,E2,…,EN-1,EN,且EN=Ef;狀態量離散為x0,x1,x2,…,xN-1,xN,且xN=xf;控制量離散為U0,U1,U2,…,UN-1,UN。 采用梯形法則對問題P1中的線性動力學方程進行近似離散,則離散后的動力學方程為 Bj+1Uj+1+Cj+1) (49) 式中:ΔE=(Ef-E0)/N,下標j表示離散點編號,j=0,1,…,N-1。 整理式(49),可得到更簡潔的動力學方程形式,表示為 LjXj-Lj+1Xj+1+MjUj+Mj+1Uj+1=Gj (50) 完成動力學方程離散化后,再對問題P1中的其他約束和目標函數積分項進行離散化,進而得到一個凸數學規劃問題,記為問題P2,表示為 (51) 問題P2中的優化變量包括每個離散點處的狀態量xj和控制量Uj。由于N個離散間隔對應N+1個離散點,因此優化變量數目為8(N+1)。 由于問題P2中采用狀態量x和新控制量U作為優化變量,經過凸優化求解后不能直接獲得用于制導的攻角和傾側角指令,因此需要利用凸優化解進行指令反解,獲得每個離散點處相應的攻角和傾側角指令。 假設優化后第j個離散點處的狀態量為xj,新控制量為Uj=[u1,j,u2,j,u3,j]Τ,則對應攻角指令αj可利用牛頓法或反插值方法求解下列非線性方程確定。 F(αj,Maj)=u3,j (52) 式中:Maj為由xj所確定的當前馬赫數。 傾側角指令可利用式(53)確定 (53) 在問題P2的求解過程中,控制量附加約束很難保證在每個離散點處都滿足等式成立。這里定義附加約束違反程度函數,用于定量描述該約束的違反情況,表示為 (54) 當違反程度VU超出給定容許值εU時,則由式(52)和式(53)所得的反解指令(αj,υj)是不可信的,反之,則是可信的。本文將在仿真中分析這種情況對解精度的影響。 違反程度容許值的取值可以根據如下經驗公式確定: (55) 式中:Z為經驗常數,一般可以取100~500之間。如果Z取值過大,則容許值εU較小,使得較多反解指令是不可信的;反之,若容許值較大,則大部分反解指令是可信的,則失去了判斷反解指令可信度的意義。常數Ζ的選擇應根據具體問題進行權衡確定。 由于原最優控制問題P0具有強非線性,如果僅采用一次線性化來處理非線性動力學與過程約束,即僅求解一次問題P2,則所得凸優化解對于原問題P0基本是不可行的。因此需采用連續線性化方法,對動力學與過程約束進行連續線性化,從而產生一個迭代求解序列。 在這個序列中,每次迭代都會求解一個凸優化子問題(即問題P2),利用該子問題的解再進行下一次的線性化,直至這個解序列最終滿足收斂條件。為了保證該求解序列的收斂性[15],在信賴域約束中引入松弛系數κ,并將其作為一個附加項添加至目標函數中,從而得到新問題P3,表示如下 (56) 式中:C3為松弛系數項的權重系數。 動力學約束是軌跡規劃問題中必須滿足的一個約束,問題P3所得的解僅滿足線性動力學約束,相比問題P0中的非線性約束必然存在一定誤差,定量描述這個誤差可用于表示凸優化解相對原問題P0的可行性。因此,下面定義非線性約束違反程度,用于定量描述凸優化解對原非線性動力學約束的違反情況。 求解問題P3得到的凸優化解可表示為(x(k),U(k)),通過指令反解得到的控制指令為(α(k),υ(k))。以該控制指令為輸入,對式(2)所示的原始動力學方程進行積分,得到相對于凸優化解的積分驗證解,表示為 (57) 由此可定義非線性約束違反程度,也可稱為凸優化解的近似誤差,用于表征優化后的狀態量x(k)與控制指令(α(k),υ(k))對原始非線性動力學約束的違反程度,計算公式為 (58) 該迭代算法以相鄰兩次凸優化解對應的狀態量最大偏差作為收斂準則,表示為 (59) 式中:收斂誤差限定義為ε=[εr,ελ,εφ,εθ,εσ]Τ,上述不等式左邊的表達式可定義為每個狀態量的相鄰2次凸優化解最大偏差。 基于上述分析,這里給出基于凸優化的序列凸化算法求解原最優控制問題P0的步驟: 步驟1給出一條初始參考軌跡x(0),初始參考指令(α(0),υ(0)),令k=0。 步驟2基于參考軌跡x(k)和參考指令(α(k),υ(k))計算控制量約束邊界、過程約束邊界以及線性化矩陣。 步驟3求解凸優化子問題P3,獲得凸優化解(x(k+1),U(k+1))。 步驟4利用凸優化解進行指令反解,得到新的指令序列(α(k+1),υ(k+1)),以此作為積分輸入,計算非線性動力學違反程度函數Rnonlinear。 步驟5判斷是否滿足如式(59)所示的收斂條件,若滿足,則算法結束;否則,令k=k+1,轉入步驟2。 本文采用CAV-H模型進行仿真分析[23],初始化軌跡生成方式可參考文獻[16],初始攻角指令取為20°常值,初始傾側角指令取為0°常值。邊界條件設置如表1所示,主要約束設置如表2所示。 表1 邊界條件取值Table 1 Values of boundary constraints 表2 其他約束條件取值Table 2 Values of other constraints 仿真中采用MATLAB平臺下CVX作為建模語言[24],計算精度設為1×10-6,即當相鄰2次迭代的目標函數相對變化量小于預設計算精度時,求解器迭代終止。默認SDPT3求解器求解凸優化子問題P3,運行計算機搭載Intel Core i5-3470 3.20 GHz處理器。 由于整個滑翔飛行過程中能量E一直為負值,為了顯示方便,將其轉換至[0,1]范圍內,公式為 (60) 此時由再入點開始,能量E′從0到1單調遞增。 本節主要分析所提三維剖面規劃方法優化解的可行性,并驗證該方法相比二維剖面規劃方法在發揮飛行器固有機動能力方面的優勢。這里的可行主要包括2個方面,一是優化解的狀態軌跡與控制指令(包括攻角和傾側角)之間是否滿足非線性動力學約束,二是由控制指令積分獲得的過程量是否滿足非線性約束要求。 圖1~圖5給出了本文仿真條件下利用所提方法得到的再入軌跡。其中,藍色粗實線代表的“優化解”為迭代過程收斂時最后一次求解問題P3獲得的解,以紅色點劃線代表的“積分解”由式(57) 定義可得。這里以積分解的結果作為精確值,驗證“優化解”的可行性。 圖1中對軌跡規劃的起始點進行了標注,以該點對應的狀態作為軌跡規劃的起始狀態,在此之前的軌跡狀態按照常值控制量進行積分獲得。由圖1~圖3可以看出,優化解對應的狀態量與積分解的結果基本一致,說明優化解中的狀態量與控制指令之間基本滿足原始非線性動力學約束,沒有出現較大偏差。由圖3可知,優化解對應的軌跡滿足期望目標點位置約束。 圖4給出了熱流密度、動壓和過載3項過程約束的變化規律。可以看出,優化解與積分解對應的軌跡均滿足給定的過程約束,說明相應的狀態量基本一致。同時,由凸優化模型得到的狀態量仍然滿足原始過程約束,即相對于原問題是可行的,說明應用線性化方法處理非線性過程約束在該問題中是可行的。 圖1 高度和速度變化規律Fig.1 History of altitude and velocity 圖2 速度傾角和航跡偏航角變化規律Fig.2 History of flight path angle and heading angle 圖3 地面軌跡對比示意圖Fig.3 Comparison of footprints 圖5給出了利用優化解進行指令反解得到的攻角和傾側角曲線,從控制量的角度講它們即是對三維剖面的一種表征。在規劃起點之前,攻角設置為20°常值,傾側角設置為0°常值。圖1~圖4 中積分解均是以圖5所示的控制指令為輸入進行積分獲得的。 下面定量分析優化解的可行性,主要指優化解相對于原最優控制問題的非線性約束違反程度。圖6給出了優化解對應的控制量附加約束違反程度V在所有離散點上的分布情況。可以看出,在第153~157個離散點之間,違反程度異常增大,說明這幾個離散點處的反解指令是不可信的,而其他離散點處的反解指令是可信的。 圖7給出了優化解在每個離散點處的近似誤差分布情況。可以明顯發現,在反解指令異常情況出現前后,單個離散點的近似誤差出現明顯變化,由此也導致后續離散點處的近似誤差都顯著增大。這個現象與圖2中,在歸一化能量取值0.8以后,優化解與積分解開始出現微小差異是一致的。這些誤差的產生都是由于優化解在極個別離散點處不嚴格滿足如式(21)所示的控制量附加約束引起的,而這種個別離散點處的現象一般是由于數值求解不穩定造成的。 圖4 三項過程約束變化規律Fig.4 History of three path constraints 圖5 控制指令曲線Fig.5 History of control command 表3給出了優化解與積分解的終端狀態對比結果。可以看出終端狀態偏差是比較小的,即解精度在一定范圍內是可以保證的。這也說明根據本文定義的新控制量得到的線性動力學相對于原始非線性動力學的約束誤差是有限的。所以,在一定精度條件下,由本文方法所得的凸優化解可以作為原問題的一個可行解。 圖6 控制量附加約束違反程度分布Fig.6 Violation distribution of additional constraint 圖7 逐點近似誤差分布Fig.7 Distribution of approximation error on each discretization point 表3 終端狀態對比Table 3 Comparison of terminal states 為了比較三維剖面規劃方法相較于二維剖面規劃方法的優勢,以文獻[16]中的二維剖面規劃方法為參考,仿真條件與本文相同,2種方法所得的地面軌跡對比結果如圖8所示,終端位置偏差對比結果如表4所示。可以看出,在相同條件下,三維剖面規劃方法的優化解對應的終端位置可以到達給定目標點,距離偏差為0,但二維剖面規劃方法的優化解對應的終端位置與給定目標點相距1 678.57 km。由于仿真設置的優化目標是終端位置偏差最小,此時二維剖面規劃方法的優化結果代表了其所能發揮的最大機動能力,對比而言,三維剖面規劃方法所能發揮的機動能力更大。由此可以得出,三維剖面規劃方法在再入滑翔軌跡規劃時可以充分發揮飛行器固有的機動能力。 序列凸化算法的收斂性對于該方法的可行性至關重要,本節對4.1節算例求解過程的收斂性進行分析。 根據式(59)所示的收斂準則,當序列凸化算法迭代至第15次時,各個狀態量的相鄰兩次凸優化解最大偏差分別為 |Δrj|max=78.286 6 m,|Δλj|max=0.044 5°,|Δφj|max=0.020 0°,|Δθj|max=0.045 4°,|Δσj|max=0.198 4°,滿足仿真中所給的收斂誤差限,迭代終止。 為了體現凸優化的求解效率,在相同計算條件和計算精度下,利用GPOPS 5.0偽譜法工具包求解該問題,則本文所提方法與偽譜法的比較結果如表5所示,其中,凸優化方法的求解時間由每次子問題求解輸出的CPU時間累加獲得,偽譜法的求解時間由每次迭代輸出的實際求解時間累加獲得。 由表5可以看出,凸優化和偽譜法均可獲得滿足各項約束條件的再入軌跡,實際計算精度均小于預設計算精度,2種方法獲得的性能指標差異小于10%。相比偽譜法,凸優化方法迭代次數更少,在計算效率方面具有明顯優勢。 圖9給出了序列凸化迭代過程中得到的歷次軌跡與初始化軌跡的對比結果,其中,藍色實線表示由線性假設得到的初始化軌跡,紅色點劃線表示迭代收斂后輸出的優化軌跡,其他細實線表示中間迭代解對應的軌跡。可以看出,隨著迭代次數的增加,相鄰2次軌跡的偏差逐漸減小,優化軌跡逐漸收斂。同時,收斂后的優化軌跡與初始化軌跡相差較大,說明本文所提方法的收斂性對于初始化軌跡的選擇具有一定的適應能力。 圖10給出了5個狀態量的收斂情況,所有子圖的橫軸取值從1開始。圖10(a)中高度收斂圖的縱坐標是對數坐標。本文中狀態量的收斂過程主要由相鄰2次凸優化解的最大偏差來衡量,由式(59)計算可得。總的來看,5個狀態量的收斂趨勢是比較一致的,最大高度偏差在最后2次迭代時趨于收斂,而最大速度傾角偏差在第10次迭代后趨于收斂,剩余3個最大狀態偏差則在第6次迭代后趨于收斂。這說明不同狀態量的收斂速率是不一致的。 圖11給出了信賴域松弛系數的收斂情況。可以看出,除了前2次迭代時得到的松弛系數比較大以外,后續迭代過程中松弛系數始終比較小,且最后達到收斂條件時松弛系數取值為κ*=0.002 7,說明隨著信賴域松弛系數的減小,序列迭代算法逐漸趨近于收斂。 圖10 5個狀態量收斂情況Fig.10 Convergence process of five state variables 圖12給出了最優性能指標的收斂情況,該圖中縱坐標為對數坐標。可以看出,優化目標的收斂是比較快的,基本在第6次迭代以后就趨于穩定。當序列凸化算法收斂時,目標函數中的終端位置偏差和信賴域松弛變量都將是一個小量,此時影響目標函數取值的主要是航跡偏航角的積分項,而該項的變化僅與側向運動相關。所以,經度、緯度和航跡偏航角這3個與側向運動相關的狀態量,其收斂過程與優化目標基本一致。由于目標函數中缺少縱向運動參數,所以與縱向運動相關的高度和速度傾角這2個狀態量在迭代過程中出現了較多震蕩,一定程度上降低了算法的整體收斂速率。 以上分析從數值上驗證了本文所提方法的收斂性,且收斂后的優化解僅可能是原問題的一個局部最優解,關于這種方法最優性的理論證明目前還并不充分[17]。 圖12 最優性能指標收斂情況Fig.12 Convergence process of optimal objective function 由于控制量附加約束的違反程度對于優化解精度有一定影響,因此在目標函數中引入關于航跡偏航角積分的附加項,如式(46)所示,下面分析該附加項的引入對解精度的影響。圖13給出了迭代過程中,每次迭代的解中,嚴格滿足附加約束的離散點占總離散點數目的比例變化情況。可以看出,引入附加項后,除了第8次和第11次的比例很低外,其他每次迭代解對應的比例都比較高,迭代后期這個比例值基本趨于穩定,而在不引入附加項的迭代過程中,滿足附加約束的離散點占比在后期一直較低,由此說明該附加項的引入可以有效確保附加控制量約束松弛過程的有效性。 圖14給出了迭代過程中近似誤差的收斂情況。可以看出,引入附加項后,由式(58)所定義的近似誤差在迭代過程中的收斂性是比較好的,在迭代前期很快能夠減小到一個很低的水平,說明隨著迭代算法逐步趨于收斂,凸優化解對原始非線性約束的違反程度逐漸降低,即解的精度逐步提高。但在不引入附加項的迭代過程中,由于大部分離散點處的優化值均不滿足附加約束,所以導致解精度較低。由此說明附加項的引入對于提高優化解精度是有顯著意義的。 圖13 附加項對離散點占比的影響Fig.13 Effect of additional term on proportions of discretization points 圖14 附加項對凸優化解的近似誤差影響Fig.14 Effect of additional term on approximation errors of solution by convex optimization 序列凸化算法的啟動必須依賴于一條初始軌跡。本文采用線性假設進行初始軌跡的生成,即認為運動狀態的滑翔段均是線性變化;作為對比的是以表5中提到的偽譜法所得優化軌跡作為初始軌跡。下面分析不同初始軌跡對本文所提算法收斂性的影響。圖15~圖17分別給出了信賴域松弛系數、最優性能指標和凸優化解近似誤差的收斂對比情況。 由圖15~圖17可以看出,采用偽譜法得到>的優化軌跡作為初始軌跡后,序列凸化算法在迭代12次即可達到收斂條件,而同樣條件下線性假設得到的初始軌跡需要15次迭代。由于收斂條件的參數不變,所以2組優化解的計算精度和近似誤差也基本一致。在相同計算精度條件下,由于迭代次數的減少,以偽譜法優化軌跡作為初始軌跡的迭代過程耗時也更短,由于每次迭代的CPU時間基本一致,所以節約時間比例與迭代次數的減少比例也是基本一致的。 圖15 初始軌跡對信賴域松弛系數的影響Fig.15 Effect of initial trajectory on trust region relaxation coefficient 圖16 初始軌跡對最優性能指標的影響Fig.16 Effect of initial trajectory on performance index 圖17 初始軌跡對凸優化解的近似誤差影響Fig.17 Effect of initial trajectory on approximation errors of solution by convex optimization 雖然采用偽譜法優化軌跡作為初始軌跡可以減少序列凸化算法的求解時間,但如果后者依賴于偽譜法提供初始軌跡,則凸優化的計算時間優勢將無法體現。因此,有必要尋找更快速合適的初始軌跡生成方法,從而進一步提高序列凸化算法的求解效率。 1) 建立了再入軌跡三維剖面凸優化模型,相比二維剖面可充分發揮飛行器固有的機動能力;相比偽譜法,凸優化在軌跡規劃問題上具有更高的求解效率,具備實現軌跡在線規劃的潛力。 2) 為了實現問題凸化,引入了新的控制量和附加約束。迭代求解中,在大部分離散點處該附加約束都是嚴格滿足的,個別點處的不滿足對收斂后優化解的精度影響是有限的。 3) 序列凸化方法在數值求解中具有穩定的收斂性,隨著迭代過程趨于收斂,凸優化解的精度逐漸提高。由于目標函數中主要包含側向運動項,所以側向運動狀態量的收斂速率快于縱向運動狀態量。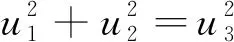
2.2 離散

3 指令反解與迭代算法
3.1 指令反解
3.2 序列凸化算法


4 數值仿真



4.1 可行性分析

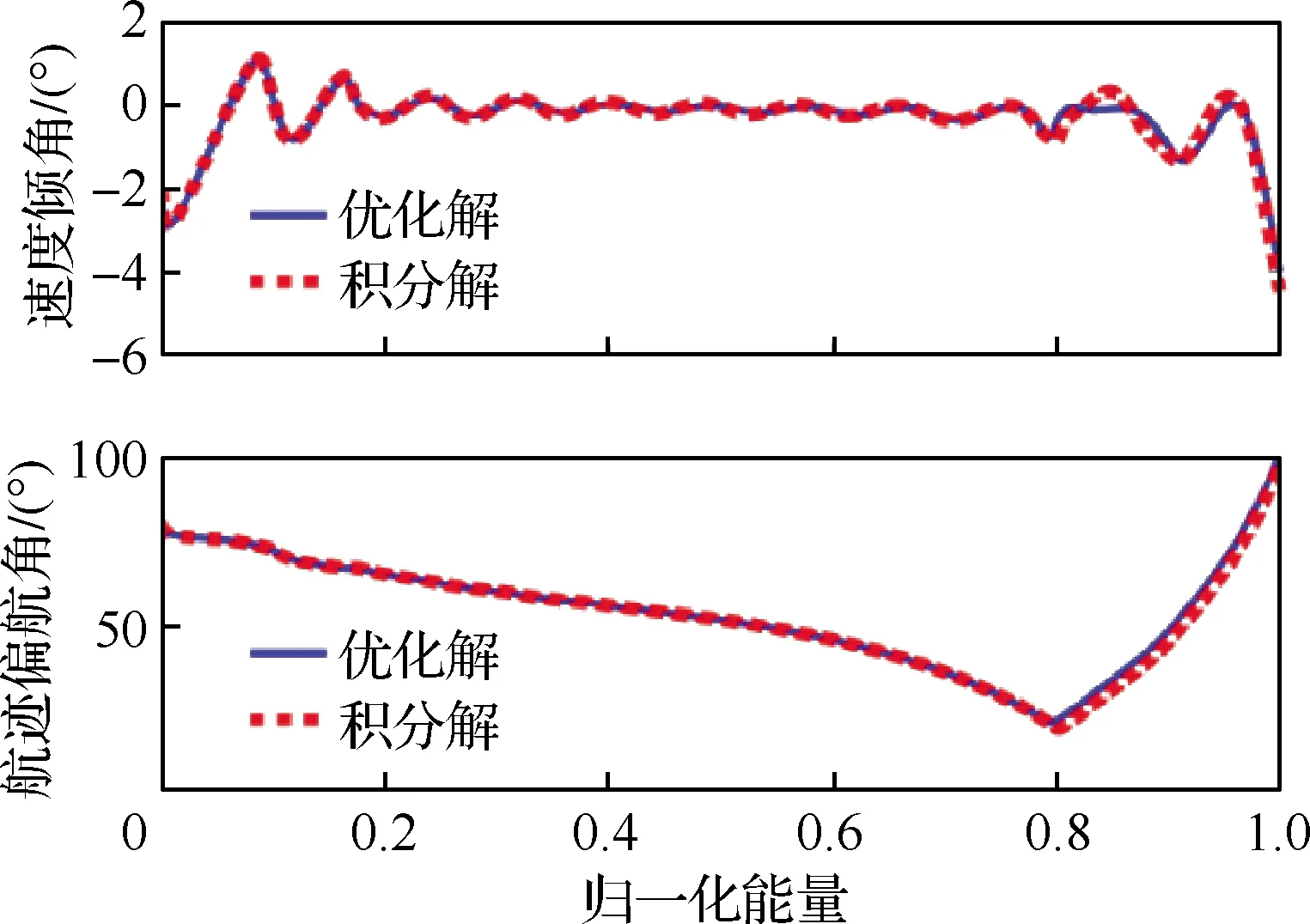





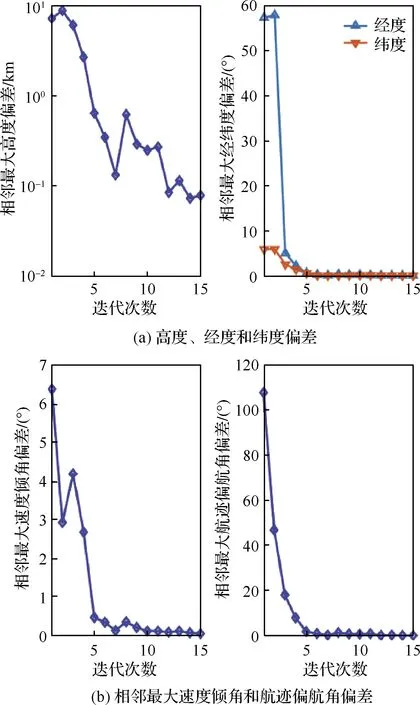
4.2 收斂性分析

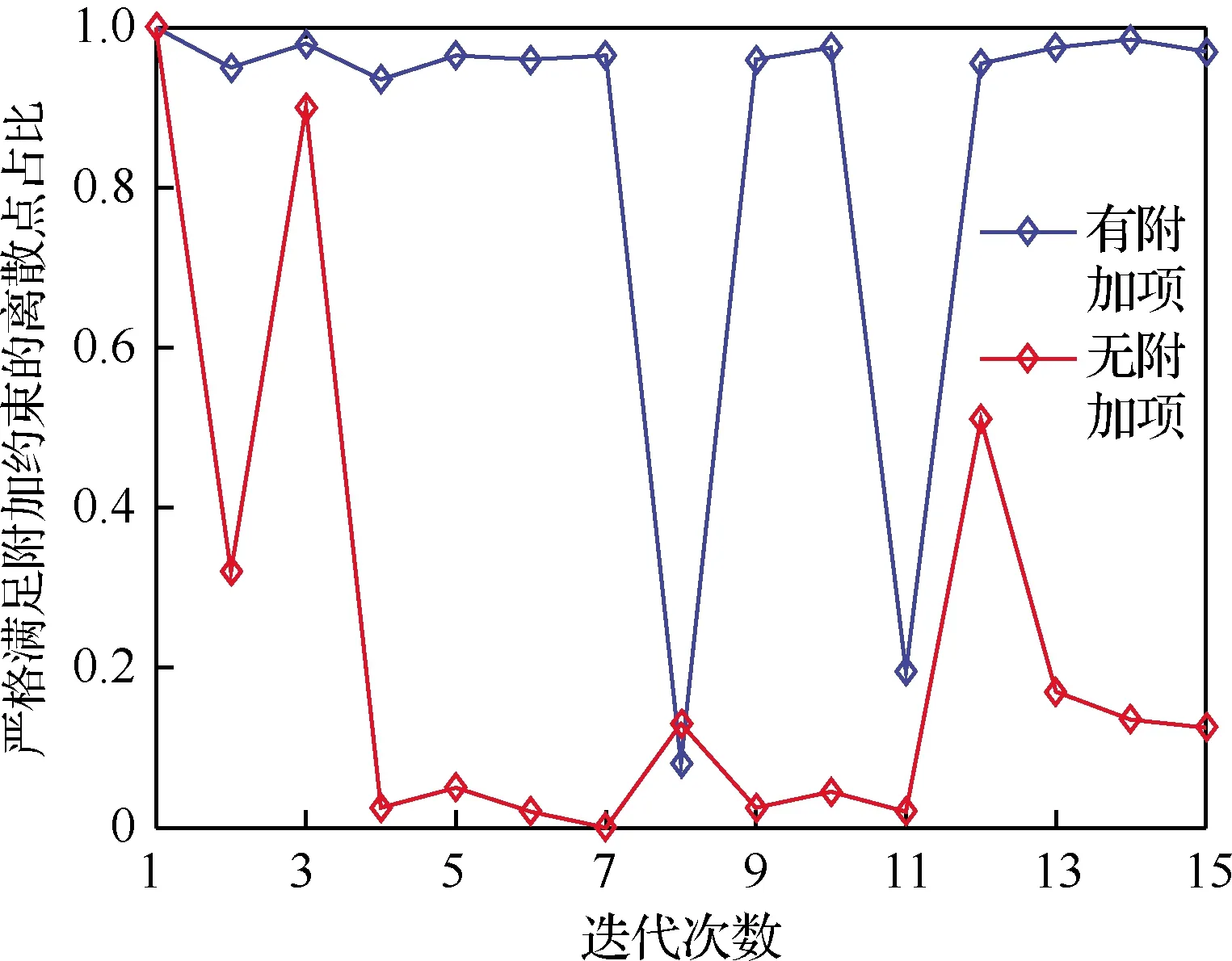


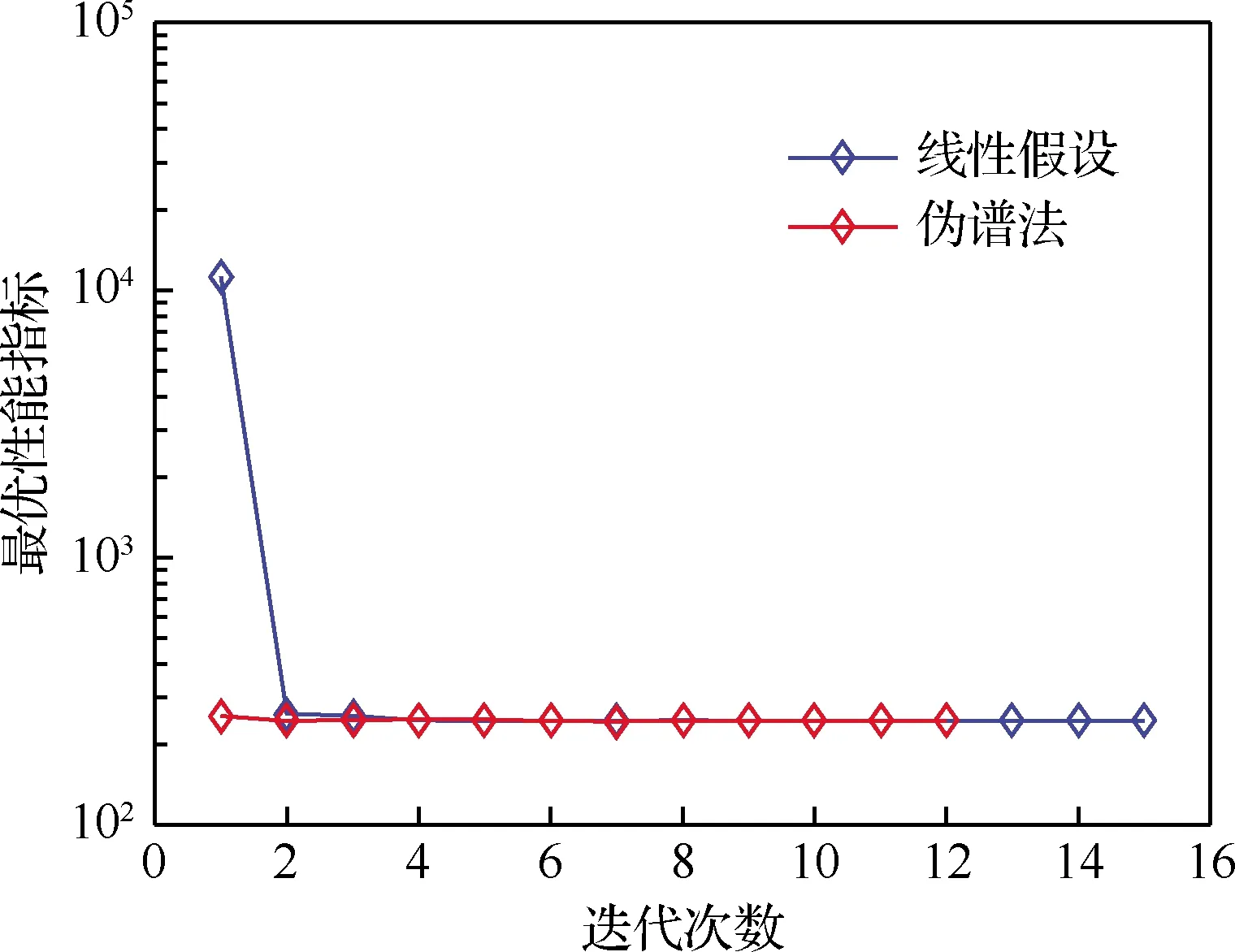
5 結 論

