基于平均擴(kuò)展速率的裂紋擴(kuò)展模型

兌紅娜，劉小冬，王凡，董江

中航工業(yè)成都飛機(jī)設(shè)計研究所 強(qiáng)度部，成都 610091

為了有效地開展外場飛機(jī)的單機(jī)壽命監(jiān)控和結(jié)構(gòu)健康管理，準(zhǔn)確的疲勞壽命預(yù)測模型是必需的。大量試驗和研究表明，基于線彈性斷裂力學(xué)(LEFM)的經(jīng)典裂紋擴(kuò)展模型無法對隨機(jī)載荷譜下(需考慮載荷順序效應(yīng))復(fù)雜金屬結(jié)構(gòu)的裂紋擴(kuò)展進(jìn)行準(zhǔn)確描述[1-2]。這類LEFM模型通常基于標(biāo)準(zhǔn)試件常幅譜疲勞試驗獲取材料參數(shù)，不能反映真實結(jié)構(gòu)幾何構(gòu)型和表面處理等因素，并且很難準(zhǔn)確模擬變幅譜載引起的載荷遲滯/加速效應(yīng)。因此，在實際工程應(yīng)用中，為了提高模型對真實結(jié)構(gòu)疲勞壽命的預(yù)測精度，通常需要用真實或類似結(jié)構(gòu)模擬件疲勞試驗對經(jīng)典LEFM模型進(jìn)行參數(shù)標(biāo)定或修正，然而，實踐表明，很難找到通用的標(biāo)定或修正方法對所有類型的載荷譜均有效[3]。

對于可產(chǎn)生穩(wěn)定裂紋擴(kuò)展速率的隨機(jī)載荷譜，如包含重復(fù)“飛-續(xù)-飛”載荷譜塊，基于平均擴(kuò)展速率的裂紋擴(kuò)展模型(下文統(tǒng)稱為平均擴(kuò)展速率模型)為隨機(jī)譜下疲勞壽命評估提供了另一種有效途徑[4-6]，該類模型將隨機(jī)譜塊當(dāng)作“當(dāng)量常幅譜”處理，通過形式簡單的經(jīng)驗公式來描述單位飛行小時(FH)的平均裂紋擴(kuò)展，用da/dt表示。這與經(jīng)典LEFM模型計算每個載荷循環(huán)(da/dN)的裂紋擴(kuò)展是不同的。

平均擴(kuò)展速率模型雖然形式簡單，但是可以對經(jīng)典LEFM模型無法準(zhǔn)確描述的隨機(jī)譜下裂紋擴(kuò)展趨勢進(jìn)行較為準(zhǔn)確的預(yù)測。與經(jīng)典LEFM模型不同的是，對于沒有進(jìn)行疲勞試驗的隨機(jī)載荷譜，如外場飛機(jī)單機(jī)使用載荷譜，平均擴(kuò)展速率模型無法直接使用，需要采用擴(kuò)展速率類比法則(下文統(tǒng)稱為速率類比法則)，借助于經(jīng)典LEFM模型，對未試驗載荷譜下的平均擴(kuò)展速率模型參數(shù)進(jìn)行合理預(yù)測。

本文對平均擴(kuò)展速率模型和速率類比法則展開詳細(xì)研究，首先介紹基于Frost&Dugdale公式和基于Paris公式的平均擴(kuò)展速率模型的內(nèi)涵及參數(shù)推導(dǎo)方法，然后通過典型機(jī)身框關(guān)鍵部位模擬件在多種隨機(jī)譜下的疲勞試驗數(shù)據(jù)對平均擴(kuò)展速率模型和速率類比法則的可行性和準(zhǔn)確性進(jìn)行深入的試驗驗證，最終給出建議和結(jié)論。

1 平均擴(kuò)展速率模型及速率類比法則

1.1 平均擴(kuò)展速率模型

平均擴(kuò)展速率模型通常基于Frost&Dugdale公式[7]和Paris公式[8]，模型中僅有2個特征參數(shù)，反映了所有復(fù)雜的載荷順序效應(yīng)及其他影響，如殘余應(yīng)力、表面處理等影響。

基于Frost&Dugdale公式的平均擴(kuò)展速率模型(下文統(tǒng)稱為Frost&Dugdale平均擴(kuò)展速率模型)，認(rèn)為裂紋擴(kuò)展速率與裂紋尺寸和應(yīng)力有關(guān)，見式(1)，該模型常用于飛機(jī)結(jié)構(gòu)概率耐久性分析，對較短裂紋段的擬合效果較好。

(1)

基于Paris公式的平均擴(kuò)展速率模型(下文統(tǒng)稱為Paris平均擴(kuò)展速率模型)，認(rèn)為裂紋擴(kuò)展速率與裂紋尺寸和應(yīng)力強(qiáng)度因子有關(guān)，見式(2)，該模型沒有解析式，只能采用數(shù)值積分法求解。相比Frost&Dugdale公式，該模型不限于較短裂紋段，可模擬更為復(fù)雜的裂紋擴(kuò)展情況。

(2)

式中：β為幾何修正因子，是裂紋尺寸的函數(shù)β(a)，無量綱，與裂紋形狀、結(jié)構(gòu)幾何構(gòu)型和邊界條件有關(guān)；C和m為Paris模型參數(shù);Kref為參考應(yīng)力強(qiáng)度因子。

模型參數(shù)值需通過結(jié)構(gòu)模擬件/部件/全機(jī)疲勞試驗來確定(推導(dǎo)方法詳見第2節(jié))，其中，結(jié)構(gòu)模擬件應(yīng)盡量模擬真實結(jié)構(gòu)部位的材料、構(gòu)型、應(yīng)力梯度、表面處理、加工工藝等。

1.2 速率類比法則

對于未進(jìn)行疲勞試驗的隨機(jī)載荷譜，如外場飛機(jī)單機(jī)使用載荷譜，無法直接使用平均擴(kuò)展速率模型進(jìn)行壽命預(yù)測，因為模型參數(shù)是未知的。這點與經(jīng)典LEFM模型不同。

因此，為了對未試驗載荷譜下平均擴(kuò)展速率模型參數(shù)進(jìn)行合理預(yù)測，提出了速率類比法則，認(rèn)為不同載荷譜下真實擴(kuò)展速率比值與理論擴(kuò)展速率比值近似相等:

(3)

式中：下標(biāo)1表示試驗載荷譜；下標(biāo)2表示未試驗載荷譜(如單機(jī)使用載荷譜)；下標(biāo)e表示基于疲勞試驗數(shù)據(jù)推導(dǎo)的速率，下標(biāo)p表示基于由經(jīng)典LEFM模型獲取的理論擴(kuò)展數(shù)據(jù)推導(dǎo)的速率。

大量研究表明，雖然經(jīng)典LEFM模型無法對隨機(jī)譜下復(fù)雜裂紋擴(kuò)展進(jìn)行準(zhǔn)確描述，但是對于不同譜載下裂紋擴(kuò)展的相對嚴(yán)重程度有較可靠的預(yù)測，這是速率類比法則成立的前提。

將Frost&Dugdale平均擴(kuò)展速率模型代入速率類比法則，有：

(4)

顯然，當(dāng)模型參數(shù)滿足式(5)時式(4)必然成立。

(5)

將Paris平均擴(kuò)展速率模型代入速率類比法則，有：

(6)

顯然，當(dāng)模型參數(shù)滿足式(7)時式(6)必然成立。

(7)

對于外場飛機(jī)，基于試驗譜下平均擴(kuò)展速率模型參數(shù)，采用上述速率類比法則，結(jié)合經(jīng)典LEFM模型，可對單機(jī)使用載荷譜下平均擴(kuò)展速率模型參數(shù)進(jìn)行預(yù)測。然后，以當(dāng)量初始裂紋尺寸(EIFS)作為初始裂紋(推導(dǎo)方法詳見第2節(jié))，采用數(shù)值積分算法，可對外場飛機(jī)關(guān)鍵結(jié)構(gòu)在任意裂紋長度下的裂紋擴(kuò)展壽命進(jìn)行預(yù)測。

2 平均擴(kuò)展速率模型參數(shù)推導(dǎo)

對于Frost&Dugdale平均擴(kuò)展速率模型，由于有解析式a=a0exp(Qt)，其中a0為初始裂紋尺寸，可根據(jù)關(guān)注裂紋段(如較短裂紋段)的擴(kuò)展數(shù)據(jù)(a,t)，采用最小二乘法直接推導(dǎo)出參數(shù)Q和a0。

對于Paris平均擴(kuò)展速率模型，由于沒有解析式，推導(dǎo)過程比較復(fù)雜。下面從疲勞試驗數(shù)據(jù)處理、模型參數(shù)擬合、當(dāng)量初始裂紋尺寸(EIFS)計算等幾個方面，對Paris模型參數(shù)的推導(dǎo)步驟展開說明。

2.1 疲勞試驗數(shù)據(jù)處理

結(jié)構(gòu)疲勞試驗通常采用斷口反推方法獲取可靠的裂紋擴(kuò)展數(shù)據(jù)(a,t)，為了擬合Paris模型參數(shù)，需進(jìn)一步獲取速率數(shù)據(jù)(da/dt,Kref)。

為了獲取較為穩(wěn)定的速率值，da/dt建議按式(8)進(jìn)行計算，假設(shè)小范圍的裂紋擴(kuò)展?jié)M足指數(shù)關(guān)系，如圖1所示，斜率dln(a)/dt由計算點(ai)和前/后點(ai-1/ai+1)采用最小二乘法獲取。前/后點的選取應(yīng)滿足與計算點的時間間隔不小于1個譜塊。

(8)

圖1 da/dt計算方法示意Fig.1 Calculation method of da/dt

計算點(ai)的應(yīng)力強(qiáng)度因子(Kref)i按式(9)進(jìn)行計算，其中幾何修正因子β(a)與裂紋形狀、結(jié)構(gòu)幾何構(gòu)型和邊界條件有關(guān)，σref通常選取最大載荷狀態(tài)下的應(yīng)力。

(9)

2.2 模型參數(shù)擬合

基于速率數(shù)據(jù)(da/dt,Kref)，采用最小二乘法對Paris模型參數(shù)C和m進(jìn)行擬合，如式(10)。普通最小二乘法中每個樣本點的權(quán)重相同，而對于裂紋擴(kuò)展壽命中低速率階段占比大的情況，加權(quán)最小二乘法更為合適，可加大低速率階段的樣本權(quán)重。

(10)

2.3 當(dāng)量初始裂紋尺寸計算

當(dāng)量初始裂紋尺寸(EIFS)指結(jié)構(gòu)細(xì)節(jié)在使用前(t=0)的假想初始裂紋尺寸(并非真實尺寸)，需要通過裂紋擴(kuò)展模型和一定裂紋尺寸點(ai,ti)來反推計算。顯然，EIFS的大小與裂紋擴(kuò)展模型和裂紋尺寸點的選取有直接關(guān)系，因此后續(xù)壽命預(yù)測所用的模型必須與EIFS推導(dǎo)所用的模型保持一致。如果反推的EIFS受載荷譜和應(yīng)力水平的影響較大，不具通用性，則說明裂紋擴(kuò)展模型選取得不合理。

反推所用的裂紋尺寸點可選取斷口分析的試驗數(shù)據(jù)初始點，也可選取一定裂紋長度點，如經(jīng)濟(jì)修理尺寸或臨界裂紋尺寸，亦可選取所有或者關(guān)注段的試驗數(shù)據(jù)點，通過最小二乘法推導(dǎo)使均方誤差最小的EIFS。若裂紋擴(kuò)展隨時間近似滿足指數(shù)關(guān)系，則不同尺寸點選取方法對EIFS的影響不大；若不滿足，則影響較大。

3 平均擴(kuò)展速率模型對比

本節(jié)選取典型機(jī)身框關(guān)鍵部位模擬試驗件(如圖2所示)3種隨機(jī)載荷譜各3個應(yīng)力水平下的疲勞試驗數(shù)據(jù)，對Frost&Dugdale和Paris平均擴(kuò)展速率模型進(jìn)行對比分析和試驗驗證。

隨機(jī)譜以500FH的飛續(xù)飛起落為一個譜塊，每組試驗經(jīng)斷口反推的裂紋擴(kuò)展數(shù)據(jù)如圖3所示。

圖2 模擬試驗件Fig.2 Representative coupon

圖3 模擬件疲勞試驗數(shù)據(jù)Fig.3 Representative coupon fatigue test data

對于Frost&Dugdale平均擴(kuò)展速率模型，根據(jù)每組載荷譜下試驗數(shù)據(jù)獲得試驗中值曲線，然后采用最小二乘法，對較短裂紋段(<2 mm)進(jìn)行擬合，推導(dǎo)參數(shù)Q和a0，列于表1。

對于Paris平均擴(kuò)展速率模型，采用第2節(jié)所述方法推導(dǎo)模型參數(shù)和每組試驗的EIFS，列于表1。其中，EIFS指每組試驗的樣本均值，“匯總”指匯總每種載荷譜序列所有應(yīng)力水平下速率數(shù)據(jù)樣本進(jìn)行參數(shù)擬合，如圖4中實線所示。

每組載荷譜的速率數(shù)據(jù)(da/dt,Kref)如圖4所示，散點表示試驗數(shù)據(jù)樣本，實線表示Paris平均擴(kuò)展速率模型對試驗數(shù)據(jù)的擬合，表中縱坐標(biāo)單位的sfh表示simulated flight hour。可見：

1) 在雙對數(shù)坐標(biāo)系下，da/dt與Kref呈明顯的線性關(guān)系，說明Paris模型成立。

2) 相同載荷譜序列不同應(yīng)力水平下速率數(shù)據(jù)趨勢基本一致，圖中僅用一條直線來擬合，說明Paris模型參數(shù)與應(yīng)力水平近似無關(guān)，與載荷譜序列強(qiáng)相關(guān)。

3) 對于譜型相似的載荷譜序列，Paris模型參數(shù)m(圖中直線斜率)近似相等，差異主要在于參數(shù)C。

采用表1 中2種平均擴(kuò)展速率模型參數(shù)，分別對每組載荷譜下裂紋擴(kuò)展壽命進(jìn)行預(yù)測，并與試驗中值壽命進(jìn)行對比。以載荷譜1為例，對比結(jié)果如圖5所示，空心圓點表示各載荷譜下的試驗中值，實心圓點表示Paris模型對整個裂紋段的預(yù)測值，實線表示Frost&Dugdale模型對較短裂紋段(<2 mm)的預(yù)測值。

綜合表1和圖5，可知：

1) Frost&Dugdale和Paris平均擴(kuò)展速率模型均具有較高的壽命擬合精度，但Frost&Dugdale模型需分開擬合短裂紋段和長裂紋段(模型參數(shù)是不同的)，而Paris模型用一組參數(shù)就能較好地擬合整個裂紋擴(kuò)展趨勢。

表1 平均擴(kuò)展速率模型參數(shù)對比Table 1 Comparison of average growth rate model parameters

圖4 試驗速率數(shù)據(jù)(da/dt-Kref)Fig.4 Test growth rate data (da/dt-Kref)

圖5 預(yù)測均值壽命與試驗中值壽命對比Fig.5 Comparison of predicted mean life and test mean life

2) Paris平均擴(kuò)展速率模型反推的EIFS受載荷譜和應(yīng)力水平影響較小，具有通用性和兼容性，而Frost&Dugdale模型推導(dǎo)的a0受載荷譜和應(yīng)力水平的影響較大，甚至相差1個量級。

3) Frost&Dugdale平均擴(kuò)展速率模型參數(shù)Q與應(yīng)力水平雖然在理論上存在冪函數(shù)關(guān)系，Q=λ(σref)α，但是實際上該關(guān)系可能并不成立，例如，根據(jù)表1中的參數(shù)值，僅載荷譜3下的冪函數(shù)關(guān)系近似成立，載荷譜1和載荷譜2均不成立。如果冪函數(shù)關(guān)系不成立，則無法根據(jù)試驗譜下的模擬件參數(shù)來推導(dǎo)真實結(jié)構(gòu)的模型參數(shù)(應(yīng)力水平是不同的)。即使冪函數(shù)關(guān)系成立，至少需要試驗譜3種應(yīng)力水平下的試驗數(shù)據(jù)，才能推導(dǎo)出較為準(zhǔn)確的參數(shù)λ和α，試驗成本較高。

4) Paris平均擴(kuò)展速率模型參數(shù)C和m與載荷譜序列強(qiáng)相關(guān)，與應(yīng)力水平近似無關(guān)；對于譜型相似的載荷譜序列，參數(shù)m近似相等。因此可將基于模擬件試驗數(shù)據(jù)獲取的參數(shù)直接用于真實結(jié)構(gòu)，并且，理論上僅需一種應(yīng)力水平下的試驗數(shù)據(jù)，可節(jié)約試驗成本。

5) 綜上，推薦使用Paris平均擴(kuò)展速率模型。

4 速率類比法則試驗驗證

基于第3節(jié)所述典型機(jī)身框關(guān)鍵部位模擬件的疲勞試驗數(shù)據(jù)，以及優(yōu)選出的Paris平均擴(kuò)展速率模型，本節(jié)對速率類比法則的合理準(zhǔn)確性進(jìn)行試驗驗證，步驟如下：

1) 選取任意2組載荷譜，分別作為式(3)中的譜1(試驗譜)和譜2(未試驗譜)。

2) 基于譜1下試驗數(shù)據(jù)，采用第2節(jié)所述步驟，推導(dǎo)譜1平均擴(kuò)展速率試驗參數(shù)，C1,e和m1,e，列于表1(已在第3節(jié)中求解)。

3) 基于經(jīng)典LEFM模型，獲取譜1和譜2下理論擴(kuò)展壽命數(shù)據(jù)，然后采用第2節(jié)所述步驟，分別推導(dǎo)譜1和譜2平均擴(kuò)展速率理論參數(shù)，C1,p和m1,p以及C2,p和m2,p。

4) 根據(jù)步驟2)和步驟3)的參數(shù)值，采用速率類比法則(式(7))，可估算譜2平均擴(kuò)展速率試驗參數(shù)，C2,e和m2,e。

5) 根據(jù)步驟4)的參數(shù)值，以譜1下EIFS作為初始尺寸(見表1，假設(shè)譜2下EIFS是未知的)，采用數(shù)值積分法，可對譜2下的裂紋擴(kuò)展壽命進(jìn)行預(yù)測。

6) 將譜2下的壽命預(yù)測值與試驗值進(jìn)行對比，以驗證速率類比法則的預(yù)測精度，此處以耐久性壽命和壽命間隔作為對比基準(zhǔn)。

在本例中，步驟3)選取4種經(jīng)典LEFM模型，分別為：Nasgro公式[9]、Nasgro公式+改進(jìn)Willenborg模型[9]、Walker公式+Closure模型[10]、Austen模型[11]，分別用LEFM1～LEFM4模型表示。具體公式詳見相關(guān)文獻(xiàn)，本文不再贅述。

選取32種載荷對比組合，采用步驟2)～步驟6)，每組載荷譜的壽命預(yù)測值與試驗中值列于表2，其中，符號“/”前后分別表示耐久性壽命和壽命間隔，前者指由EIFS擴(kuò)展至經(jīng)濟(jì)維修尺寸(這里取0.8 mm)，后者指由可檢裂紋尺寸(這里取1.27 mm)擴(kuò)展至臨界裂紋尺寸。

在32種載荷對比組合中，一類是相同應(yīng)力水平不同載荷譜序列，如:S2_from_S3_at_332.02表示在σref=332.02 MPa時由載荷譜3試驗數(shù)據(jù)預(yù)測載荷譜2擴(kuò)展壽命；另一類是相同載荷譜序列不同應(yīng)力水平，如:S3_at_332.02_from_349.5表示對于載荷譜3由σref=349.5 MPa的試驗數(shù)據(jù)預(yù)測σref=332.02 MPa的擴(kuò)展壽命。

對比分析表2中數(shù)據(jù)，可知：

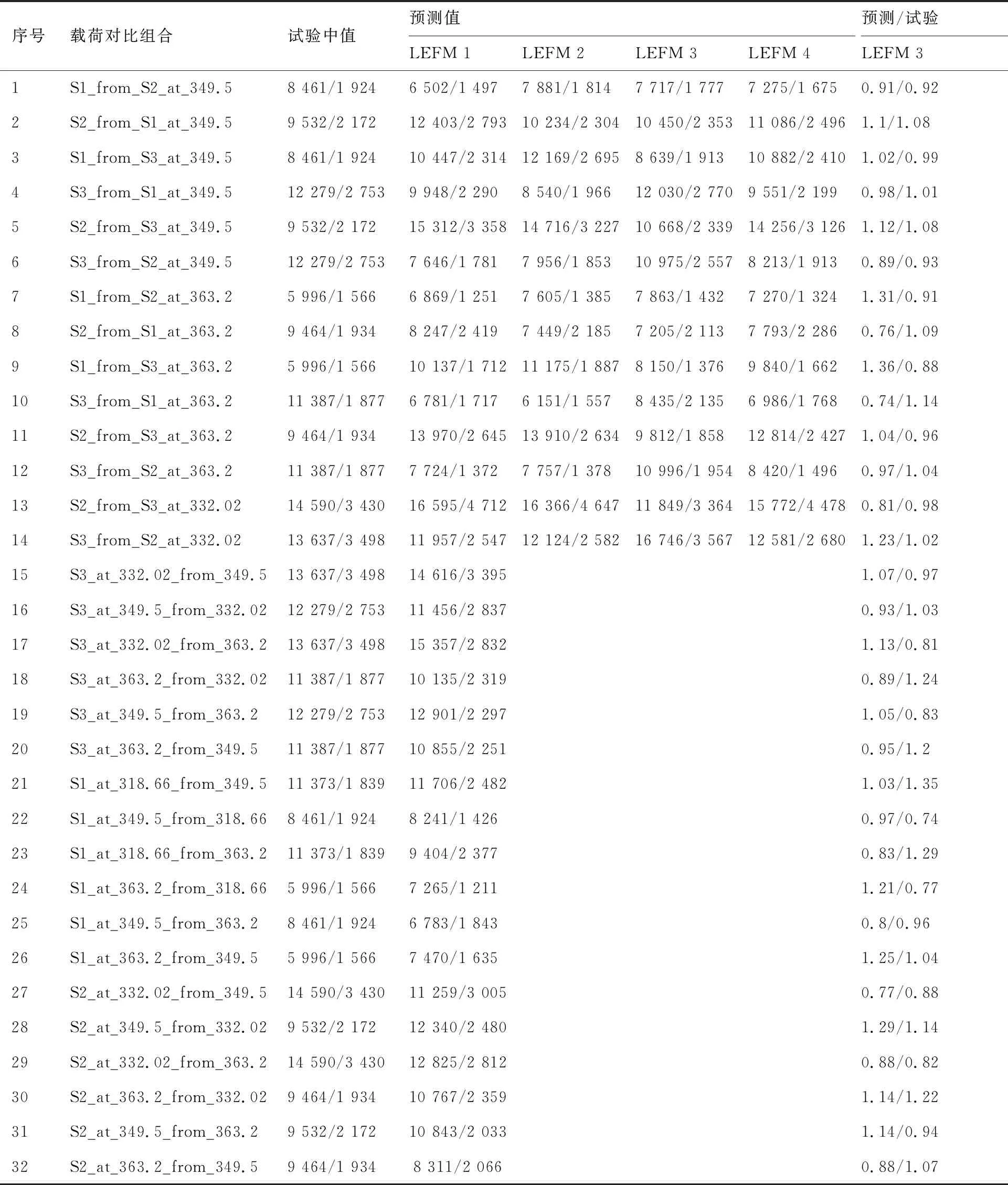
表2 基于平均擴(kuò)展速率模型的裂紋擴(kuò)展壽命預(yù)測值Table 2 Crack predicted life with average growth rate model

1) 對于相同應(yīng)力水平不同載荷譜的對比組合(序號1～14)，若2種載荷譜的EIFS均值相差較大，則耐久性壽命的預(yù)測精度稍差些，如序號7～10。由于壽命間隔與EIFS無關(guān)，因此壽命間隔的預(yù)測精度比耐久性壽命高。

2) 對于相同載荷譜不同應(yīng)力水平的對比組合(序號15～32)，由于直接采用已知載荷譜的模型參數(shù)(無需速率類比)，因此預(yù)測精度不僅與2種載荷譜的EIFS均值差異有關(guān)，還與模型參數(shù)C的差異有關(guān)。

3) 在這4種理論模型中，速率類比公式采用LEFM3模型的壽命預(yù)測精度最高，預(yù)測值與試驗中值的比值在0.76～1.36，大部分位于0.9～1.1。可見，速率類比法則的準(zhǔn)確度與經(jīng)典LEFM模型的選取有關(guān)。

繪制基于速率類比法則(采用LEFM3模型)的壽命預(yù)測值與試驗中值的相關(guān)圖，如圖6所示，圖中虛線表示y=1.5x和y=x/1.5。進(jìn)一步采用統(tǒng)計檢驗方法，發(fā)現(xiàn)：壽命預(yù)測值與試驗中值的比值服從正態(tài)分布，概率密度函數(shù)如圖7所示，均值mean≈1，標(biāo)準(zhǔn)差std<0.17，驗證了速率類比法則具有較高的預(yù)測精度。

圖6 壽命預(yù)測值與試驗中值的相關(guān)圖Fig.6 Correlation plot of predicted life and test life

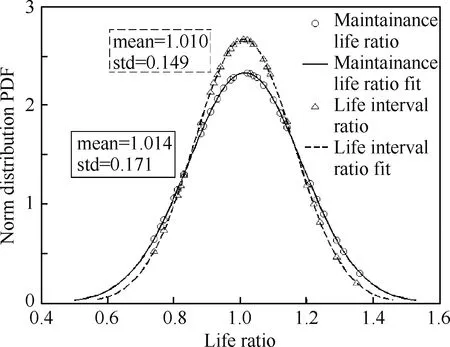
圖7 壽命比值的正態(tài)分布擬合Fig.7 Norm distribution fit of life ratio

5 結(jié) 論

本文對基于Frost&Dugdale公式和基于Paris公式的平均擴(kuò)展速率模型和速率類比法則展開詳細(xì)研究，并通過典型機(jī)身框關(guān)鍵部位模擬件在多種隨機(jī)譜下的疲勞試驗數(shù)據(jù)進(jìn)行深入的試驗驗證，具體總結(jié)如下：

1) 平均擴(kuò)展速率模型用形式簡單的經(jīng)驗公式來描述隨機(jī)譜下單位飛行小時的平均裂紋擴(kuò)展，該模型將隨機(jī)譜當(dāng)作“當(dāng)量常幅譜”處理，經(jīng)驗證對試驗隨機(jī)譜下裂紋擴(kuò)展速率和裂紋擴(kuò)展壽命具有較高的擬合精度。

2) 基于Frost&Dugdale公式的平均擴(kuò)展速率模型通常需分開擬合短裂紋段和長裂紋段(模型參數(shù)是不同的)，基于試驗數(shù)據(jù)推導(dǎo)的a0受載荷譜和應(yīng)力水平的影響較大，且參數(shù)Q與應(yīng)力水平的冪函數(shù)關(guān)系實際上可能并不成立。

3) 基于Paris公式的平均擴(kuò)展速率模型能較好地擬合整個裂紋擴(kuò)展趨勢，基于試驗數(shù)據(jù)反推的EIFS受載荷譜和應(yīng)力水平的影響較小，且模型參數(shù)與應(yīng)力水平近似無關(guān)，推薦使用Paris公式。

4) 經(jīng)試驗驗證，速率類比法則近似成立，但速率類比法則的準(zhǔn)確度與經(jīng)典LEFM模型的選取有關(guān)，不同結(jié)構(gòu)不同疲勞關(guān)鍵部位所適用的經(jīng)典LEFM模型可能是不同的。

5) 經(jīng)試驗驗證，采用基于Paris公式的平均擴(kuò)展速率模型，結(jié)合速率類比法則，可實現(xiàn)隨機(jī)載荷譜下裂紋擴(kuò)展速率和壽命的高精度預(yù)測，為外場飛機(jī)單機(jī)壽命監(jiān)控提供了一種可靠的疲勞壽命預(yù)測方法。