機制砂高強混凝土強度和彈性模量試驗研究

劉曉龍

（中鐵十六局集團第一工程有限公司， 北京 101300）

0 引言

隨著我國建設事業的迅速發展，基于混凝土設計的主要趨勢，越來越多的大型土木工程項目要求河砂作為普通細集料。河沙枯竭可能發生在許多地方，特別是遠離任何河流的地方。在這種情況下，使用機制砂可能是一個簡單可行的選擇。與河砂相比，機制砂具有一些優點，如可以存在聚晶微粉(AMF)。關于 AMF 在機制砂混凝土(MSC)性能方面的作用，有相互矛盾的報道。一些研究人員報告了在 MSC 中隨著 AMF 含量的增加，坍落度減少和需水量增加。另一些文獻認為，對于 MSC 的性能而言，AMF 存在一個最佳含量，AMF 的存在可能有助于獲得更高的抗壓強度。據報道，抗壓強度受到許多不同因素的影響，這可能導致不同的報道結果。研究發現，AMF 對水泥漿體流變性能的影響受到表面性質、粒徑和礦物類型的影響。

1 機制砂混凝土性質概述

機制砂是用碎石或碎石經機械破碎分離而成的粒徑小于5mm 的人造砂，近年來已成為河道防護用天然砂的替代品。與天然砂相比，機制砂具有表面粗糙、棱角多、石粉含量大等特點。在傳統的生產工藝中，碎石或礫石直接放入破碎機中，粒度小于75 μm 的石粉易與泥塊或風化層中形成的泥粉混合。因此，對于機制砂中石粉對混凝土性能的影響有不同的看法。為了避免石粉的不利影響，現行《建筑用砂標準》(GB/T14684-2001)對 C30-C60級澆注混凝土的機制砂石粉含量相對嚴格的限值低于5.0% ，極大地限制了機制砂在結構混凝土中的應用。

2 機制砂混凝土試驗探究方法概述

機制砂由機械按照一定的破碎和篩分工序用碎石制成，具有不同于天然砂的許多特性，如不規則多邊形顆粒尖銳、表面粗糙新穎、充滿石粉等，使混凝土在新鮮和硬化狀態下具有不同的性能。因此，近年來我國對機制砂混凝土進行了大量的研究。作為結構設計的基礎，在混凝土與機制砂混合時，應清楚地了解混凝土的基本性能，包括抗壓強度、抗拉強度、斷裂模數和彈性模量之間的關系。然而，以往對機制砂混凝土的研究很少涉及這一方面。關于這些屬性的部分測試數據在已發布的參考文獻中被分離。在這種情況下，我國現行的混凝土結構設計規范沒有對機制砂混凝土與普通天然砂混凝土進行區分，也沒有對其適應性進行綜合評價。本文在總結已發表文獻的試驗數據的基礎上，通過統計分析，探討了機制砂混凝土的上述性能之間的關系，并與普通混凝土進行了比較。對機制砂混凝土這些性能的設計應用提出了一些建議。

然而，為了確保石粉的極限含量，盡可能地消除粉末泥漿，傳統的機制砂方法往往將水洗作為最終的測定方法。由此產生了兩個問題: 一是機制砂中大量石粉被沖刷出來排入河道造成的二次環境污染，二是混凝土綜合利用中自然資源的浪費。針對這一情況，提出了將傳統的水洗工藝改為第一步工藝的技術改進方案，使石材在破碎前進行清洗，避免將泥漿混入原料中，最后保留完整的石材粉末。與傳統的機制砂不同，全石粉砂被稱為原機制砂。原機制砂中石粉的含量一般都超過規定的限量。

3 機制砂混凝土強度和彈性模量試驗

3.1 機制砂混凝土軸向壓縮強度與立方壓縮強度的理論關系研究

首先本文從已有的文獻中收集了55 組試驗數據，混凝土的立方抗壓強度范圍為28.8 MPa 至102.5 MPa。通過統計分析，軸向壓縮強度與立方體壓縮強度之間的關系符合0.947 的關系系數和0.081 的標準差，GB50010 中規定的普通混凝土的關系式和機制砂的試驗結果進行對比能夠得出，普通混凝土的試驗結果在混凝土立方抗壓強度測試值小于60MPa 時接近試驗值的下限，而混凝土立方抗壓強度大于60MPa 時接近于標準中提出的公式關系。因此，GB50010 中規定的普通混凝土的關系式可用于結構設計機制砂預測混凝土的軸向抗壓強度。在已有試驗研究的基礎上，原機制砂性能和石粉摻量對新拌混凝土工作性能和硬化混凝土性能有不同的影響。為此，進行了原機制砂、石粉固有特性的系列試驗，研究了石粉含量對砂性能和水泥砂漿強度的影響，并介紹了主要試驗結果。

3.2 原機制砂石粉含量對強度發展的影響試驗探究

在實驗的過程中選擇具有合格穩定性的42.5 級普通硅酸鹽水泥和具有已知的物理力學性能的原機制砂進行試驗。對原機制砂進行分選和測定后，重新調整了具有砂質的石粉含量。5 毫米-10 毫米和10 毫米-25 毫米系列的石灰石粉按1:1 的比例混合，并且對其物理和機械性能進行檢測和記錄。在混凝土配比的控制方面將混凝土的設計等級為 C50，只需改變石粉含量分別為3% 、7% 和13% ，減水劑含量為水泥質量的0.75% 。試驗方法符合《普通混凝土力學性能試驗方法標準》(GB/T50081-2002)的規定。對150mm 的立方體進行了3 d、4 d、7 d、14 d、28 d、56 d、90 d、120 d、150 d 和180 d 的立方體抗壓強度測試，共測試了27 個周期。

首先對砂礫的特征進行研究和分析，圖1 示出了天然砂和原機制砂的圖片，可以看出天然砂呈淡黃色，顆粒較大的圓形平原表面，粉砂含量較高，原機制砂呈凹凸灰色，顆粒呈不規則多邊形顆粒狀，表面粗糙，邊緣尖銳，石粉含量較高。粒度特征通常用點狀、長寬比和豐滿度三個指標來描述。指向性反映了籽粒邊緣和角點的相對敏銳度，長寬比用于評價籽粒是否呈針狀，豐滿度是與籽粒表面光滑程度有關的籽粒凸度的度量。與天然砂相比，原機制砂的點狀和長寬比較大，含有更多的針狀顆粒。然而，天然砂由于長期磨損而表面光滑，所以充滿率較大。

圖1 天然砂(左)和原機制砂(右)的外觀示意圖

原機制砂的顆粒特性一般會導致顆粒之間產生較大的機械嚙合力，有利于砂與水泥的粘結，但不利于新拌混凝土的流動性，在拌制混凝土時應予以注意。

之后對于砂礫的級配進行統計和分析，根據顆粒組成的統計分析，天然砂屬于 II 級配上下限中間具有理想級配曲線的中型砂，原機制砂屬于末端過粗級配、中間極少級配的粗砂，顆粒大于2.36 mm 或小于0.15 mm，但小于0.6 mm ー1.18 mm，符合 I 級配砂的技術要求。砂的級配對于控制新拌混凝土的含水量具有重要意義。4.75 mm 至0.15 mm 的顆粒效果更好，特別是4.75 mm 至2.36 mm 的顆粒效果更好。因此，應采取相應的措施來滿足新拌混凝土的工作性能。

在此基礎上對機制砂的細度分布進行分析和研究，圖2 示出原機制砂中石粉的細度分布和各粒度級的合格率。原石粉的平均粒徑為29.99 μm，小于75 μm 的顆粒含量為90.2% ，小于10 μm 的顆粒含量為24.6% ，小于10 μm 的顆粒含量為25.5% ，小于30 μm 的顆粒含量為40.2% 。由于水泥漿體系中石粉微細顆粒的填充作用以及集料孔隙等因素的影響，石粉細度呈均勻連續分布，有助于提高混凝土的密實度。根據相關研究，石粉的微細晶粒，尤其是小于10μm 的微細晶粒，有促進水泥水化的晶核效應。

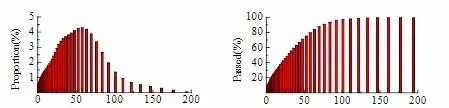
圖2 細度分布(左)及各粒度級石粉的通過率

通過試驗能夠得出不同石粉含量、不同時間的混凝土抗壓強度的發展情況。石粉含量對砂性能的影響從圖3 可以看出，在0.15ー2.36 mm 的水平范圍內，石粉含量對篩子累積剩余量(ATR)的影響為負相關，相關系數大于0.99。根據試驗數據，可將分級范圍劃分為0.6 mm 水平篩余物的累計剩余量。當石粉含量低于6% 時，砂的級配屬于 I 級。當含量在6% ー14% 之間時，屬于范圍 II。當含量在14% ー20% 之間時，屬于范圍 III。

圖3 石粉含量對砂級配的影響示意圖

綜合來看，原機制砂的石粉含量在試驗范圍內是合適的。通過試驗研究了原機制砂、石粉的性能，以及石粉摻量對砂性能和水泥砂漿強度的影響。研究結果有助于解釋原機制砂在不同石粉摻量下混凝土的一些特性。與普通混凝土相比，混凝土的增量更為理想。并且根據得到的混凝土配比對機制砂強度的影響機制關系能夠對混凝土的強度進行有效準確的預測，原機制砂中的石粉對混凝土強度的影響與普通機制砂中摻入石粉的混凝土強度的影響差別很大，原機制砂中石粉含量低于5% 的極限值不適合用于 C50 級混凝土。

3.3 石粉摻雜量對機制砂的彈性模量的影響試驗探究

在進行石灰石彈性模量檢測的過程中利用高摻量石粉制備高強高性能混凝土，以擴大石灰石粉碎廢料的應用范圍，實現石灰石粉碎廢料的利用。采用52.5 級普通硅酸鹽水泥，3 天抗壓強度為30.3 MPa，28 天為62.4 MPa。礦物摻合料為I 級粉煤灰(FA)和磨細高爐礦渣（GFBS）。粗集料為5ー25mm 連續級配的石灰石碎料。采用兩種不同的砂作為細集料。第一種是細度模數為3.4 的石灰石砂，原始粉塵含量(＜ 75μm)為3.5% 。用河砂與質譜進行比較，其細度模數為2.7。采用濕篩法從剩余石灰石砂中分離出目數小于75μm 的石灰石粉塵。采用105 ° c 干燥24h，研磨至75μm 的方法制備粘土粉。摻合料為 JG-2 高效減水劑和 JG-3 緩凝超級塑化劑，按重量1:1 混合。

人們普遍認為，混凝土的彈性模量取決于其抗壓強度、體積密度、骨料的相對體積和剛度(剛度與骨料來源密切相關)。本文的結果表明，MS 混凝土與 RS 混凝土的彈性模量沒有明顯差別，微細粒含量最高的 MS 混凝土的彈性模量為14% ，而 MS 混凝土的彈性模量隨微細粒含量的增加而降低。微細粉含量的增加，一方面改善了混凝土的抗壓強度，使彈性模量趨于增加，但另一方面增加了漿體體積，然后降低了混凝土的彈性模量。用 FA 或 GBFS 替代水泥后，材料的彈性模量降低。

4 結束語

綜上所述，機制砂具有不規則多邊形顆粒尖邊、表面粗糙、石粉含量大等特點，對混凝土的性能影響不大。作為混凝土結構設計的基礎，必須清楚地了解混凝土的基本力學性能，如抗壓強度、抗拉強度、斷裂模數和彈性模量之間的關系。本文總結了已發表文獻中的試驗數據，并通過與普通混凝土的統計分析比較，討論了這些性能之間的關系。結果表明，按照我國現行規范中規定的普通混凝土的抗拉強度計算公式，可以預測混凝土的軸壓抗壓強度和抗拉強度，但當混凝土強度等級低于 C30 時，預測抗拉強度應乘以減小系數。機制砂混凝土的彈性模量大于普通混凝土的彈性模量，本文應用公式進行展望。同時，提出了斷裂模數的計算公式。