基于改進的最大均值差異算法的深度遷移適配網絡

鄭宗生，胡晨雨*，姜曉軼

（1.上海海洋大學信息學院，上海 201306；2.國家海洋信息中心，天津 300171）

（?通信作者電子郵箱1105814265@qq.com）

0 引言

遷移學習作為一種新的機器學習框架，放寬了訓練和測試數據必須服從同概率分布的前提條件，旨在將源環境中學到的知識運用到相關環境，以輔助新任務的完成，在一定程度上提高了機器學習模型的泛化能力［1］。如今，遷移學習在計算機視覺、文本分類、自然語言處理等領域均有廣泛應用［2-4］。目前國內外學者對遷移學習算法的研究主要致力于：在半監督遷移學習［5］中，最大限度地利用源域中有標注樣本，解決目標域中少量未標注樣本的問題，以減少數據標注成本。如Wang 等［6］提出基于知識遷移的算法，通過構建兩個域中潛在的同構特征空間來學習域不變模型。Khan等［7］通過計算兩域概率密度比值給源域樣本賦權重，篩選源域樣本輔助目標域訓練。大多數遷移學習算法均是建立在兩域樣本的特征空間和邊緣概率分布差異較小的前提下，當源域和目標域樣本間的域差異較大時，如何利用遷移學習算法在小樣本目標域上構建出良好的模型成為研究的重點。

隨著深度卷積神經網絡（Deep Convolutional Neural Network，DCNN）在自動分析和圖像特征識別方面不斷取得卓越成果［8-10］，遷移學習廣泛地與卷積神經網絡相結合，基于參數的遷移學習算法通過共享模型結構或先驗參數以實現目標任務。近期研究顯示，DCNN 通過處理樣本間變量的解釋性因素，并根據特征與不變因素的關聯程度將其逐層提取，從而能夠學習到更多可遷移的特征［11］。Yosinski 等［12］通過逐層分析AlexNet網絡的特征遷移能力，得出影響網絡遷移能力的兩個關鍵因素：1）卷積層間脆弱的互適應性；2）高層全連接層中神經元的特化性。針對全連接層的特化性，Long 等［13］提出深度適配網絡（Deep Adaptation Network，DAN），保留AlexNet卷積層間脆弱的互適應性，對全連接層進行逐層適配從而進一步減小源域和目標域樣本間的差異，提高網絡遷移能力。AlexNet 網絡中互適應層數較少，模型遷移能力不受影響，然而深度卷積神經網絡中的互適應卷積層數較多，在兩域樣本差異［11］較大的情況下，保留層間的互適應性，勢必會降低遷移模型在小樣本目標域上的性能。

針對跨領域建模問題，域差異是基于參數遷移算法的主要障礙，領域適配［14］集中解決當樣本取自不同但相關的域所存在的概率分布差異問題。最大均值差異（Maximum Mean Discrepancy，MMD）［15］作為一種度量概率分布差異的準則，是基于特征的遷移算法常用的適配方法。它利用核學習方法將樣本投射到高維的再生核希爾伯特空間（Reproducing Kernel Hilbert Space，RKHS）中，通過對樣本嵌入到RKHS 中分布的無偏估計，度量兩域樣本在RKHS 中的分布距離，顯式地減少兩域的邊緣概率分布，使其在RKHS 中的分布更加相似。如Pan 等［16］提出了最大均值差異嵌入（Maximum Mean Discrepancy Embedding，MMDE）的核學習方法，在最小化MMD 距離的同時最大化核嵌入方差，通過核主成分分析（Kernel Principal Component Analysis，KPCA）得到數據的領域不變嵌入特征。Long 等［17］提出基于聯合MMD 的適配正則化框架，重點解決條件分布概率的適配問題，并通過RKHS 中的表出定理給出模型的凸優化解。在DAN 中，Long等［17］將多核MMD作為多層適配的指標，通過顯式地減小兩域在全連接層間的分布差異，增強特征遷移能力。傳統MMD算法對樣本計算核嵌入無偏估計的時間復雜度為O(n2)，然而深度卷積網絡中參數眾多、當源域和目標域樣本在數量級和維度上較龐大時，傳統MMD算法消耗較多計算時間，占用大量存儲空間，造成資源浪費。

臺風是一種破壞力極強的災害性天氣，對臺風的強度等級預測一直是國內外研究的熱點。傳統的數據預報模型、Dvorak分析法計算過程復雜且需要大量專業知識，主觀性強，增加了分析誤差。對于復雜的氣象云圖，淺層卷積網絡特征提取不充分，分類效果不佳。深層卷積網絡開發難度大，在臺風云圖數據樣本小的情況下，過擬合現象嚴重。針對上述問題，鄭宗生等［18］引入了遷移學習思想，通過遷移模型參數微調再訓練的方法，構建了適用于臺風小樣本數據集的遷移預報模型T-typCNNs。以T-typCNNs 模型為基礎，本文提出一種基于模型和特征遷移算法相結合的多層卷積適配（Multi-Convolution Adaptation，MCA）深度遷移框架。該框架利用L-MMD 度量算法對T-typCNNs 中存在的大量互適應卷積層（即微調自適應層）進行逐層領域適配，減小兩域樣本的分布差異和網絡層間脆弱的互適應性對T-typCNNs 模型遷移能力的影響。此外，對于臺風和ImageNet 樣本在RKHS 中的核平均嵌入方式，L-MMD 算法采用線性的無偏估計，在樣本數量較多、網絡層數較深的情況下，降低計算的時間復雜度。實驗證明，對于監督遷移學習，MCA 深度遷移框架中基于L-MMD正則項的CE-MMD 損失函數在T-typCNNs 模型上的收斂速度更快，L-MMD算法較其他度量算法的分類精度更高。

1 MCA深度遷移框架設計

T-typCNNs 模型［18］是在ResNet50 網絡基礎上構建的臺風預報遷移模型。該模型遷移了ResNet50 整體卷積層結構，并根據適配出的最佳遷移層數，凍結前110 層所對應的權重參數，剩余層參數在臺風數據集上作自適應微調，最后自定義一個全連接層和Softmax分類層。

在T-typCNNs 模型基礎上，本文提出的MCA 深度遷移框架對自適應卷積層參數的更新規則增加了約束，具體結構如圖1所示。圖1中：C1～Cm是T-typCNNs中凍結的部分卷積層，Cm+1～Clast是剩余的網絡自適應層。將源域樣本（ImageNet 子數據集）和目標域樣本分別輸入到ResNet50 網絡（凍結整體網絡層參數不更新）和T-typCNNs 模型中，分別提取第Cm+1～Clast層的特征圖表示，并將兩域在每個自適應卷積層間的最大均值差異作為參數更新的規則，構建出基于T-typCNNs模型的MCA深度遷移框架。

圖1 MCA深度遷移框架Fig.1 Deep transfer framework of MCA

2 基本理論

2.1 傳統T-typCNNs模型損失函數

T-typCNNs 在利用殘差δ 進行反向傳播時，對自適應層參數進行微調，使得損失值在迭代中不斷減小，直至模型趨于收斂。T-typCNNs模型的損失函數定義為：

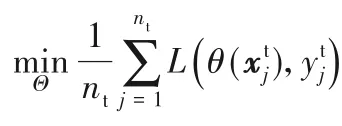
其中：L(·)是交叉熵函數；nt是目標域樣本數是網絡整體參數是樣本的原始輸入是樣本對應的標簽；θ(·)代表T-typCNNs 模型，對于網絡中的自適應卷積層，每層l 通過卷積操作和激活函數學習一組非線性映射其中分別是第l 層的權重和偏置，是樣本在第l 層的特征圖表示。在反向傳播過程中，交叉熵函數僅利用標簽維度的殘差δ 對網絡層參數進行更新，使得模型收斂速度慢且分類精度不高。

2.2 度量算法MMD

在領域適配學習中，源域Ds樣本定義為{x1，x2，…，xns}并服從分布p，ns是源域樣本數。目標域Dt中樣本定義為{y1，y2，…，ynt}并服從分布q，nt是目標域樣本數。函數φ：χ →Hk將樣本映射到高維RKHS，其中χ是樣本的特征空間。不同域在RKHS 中的分布情況——核平均嵌入（kernel mean embedding）可以有效匹配。對于核平均嵌入的無偏估計，通過計算樣本映射到RKHS 中的期望值得到，其中φ(xi)是樣本xi通過高維函數映射到RKHS 的表示形式。

最大均值差異（MMD）旨在通過高維映射函數找到兩個域樣本在RHKS中期望差值的上確界。即：

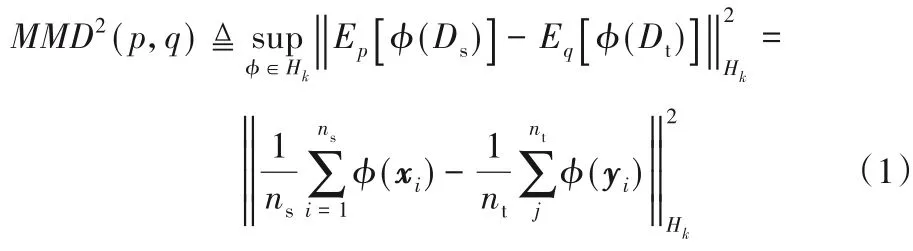
RKHS 是一個完備的高維內積空間，φ(xi)和φ(yi)的點積運算可以用核函數k(xi，yi)計算，一般選擇徑向基函數（Radial Basic Function，RBF）中表示無窮維的高斯核：

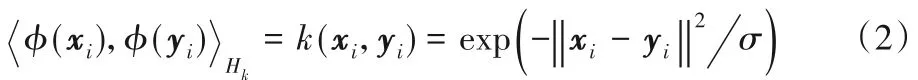
其中：σ是高斯核的帶寬。式（1）可以寫成：

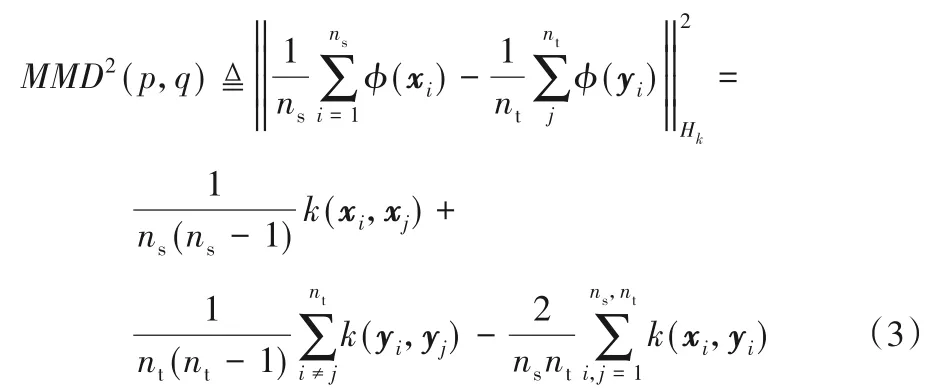
從式（3）可以看出，當p=q 時，顯然MMD2(p，q)=0；當p ≠q時，尋找使得MMD2(p，q)最小化的映射函數k(·)，使得兩域樣本在RKHS 中的概率分布在φ(·)表示下更為相似，減少在RKHS 中的分布差異。兩域樣本在數量和維度上都很龐大，對樣本嵌入到RKHS 進行無偏估計時，傳統MMD 算法的時間復雜度為O(n2)，會消耗較多計算時間，占用大量存儲空間，造成資源浪費。

針對上述問題，在Long 等［17］提出的DAN 中，對樣本嵌入到RKHS 中的無偏估計進行改進。定義一個四元組該四元組分別包括兩個源域樣本和目標域樣本，四元組上計算出的MMD為：

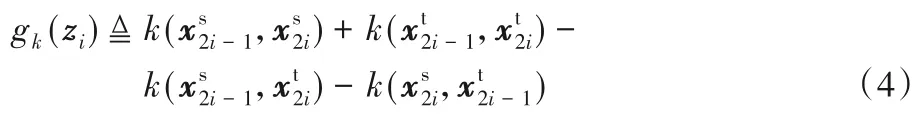
以zi為單位，兩域總體樣本間的MMD定義為：

從式（5）可以看出，DAN 中計算核平均嵌入的時間復雜度為O(n)，在保證領域間樣本充分適配的同時，減輕了計算負擔；在不影響模型性能的前提下，縮短了訓練時間。然而，DAN 中的線性嵌入法是基于源域和目標域數據擁有相同的特征空間、細微的概率分布差異、樣本數量級相當的前提下，然而當域差異（domain discrepancy）較大時，此改進的核平均嵌入算法無法充分適配兩域樣本和顯式地減小域分布差異。

3 改進算法

3.1 改進的領域適配算法L-MMD

T-typCNNs凍結了部分卷積層，即在誤差反向傳播過程中此部分參數不更新，僅需要考慮自適應微調的卷積層參數變化。源域樣本和目標域樣本在第l 卷積層的特征圖表示為卷積得到的特征圖依舊服從原始輸入的概率分布。為了方便敘述，以每個mini-batch 為單位，分別表示源域和目標域中一個batchsize的樣本數量，即且ns?nt。分別表示源域和目標域樣本在第l卷積層的特征圖表示，即代表網絡中自適應層的第一個卷積層，Clast代表最后一個自適應卷積層，即T-typCNNs的瓶頸層。

T-typCNNs 在誤差反向傳播過程中以batchsize 為單位更新權重參數，樣本的第i 個batchsize 在第l 卷積層中呈元組形式：

L-MMD 算法利用核函數將樣本嵌入到RKHS 空間，并對樣本分布進行無偏估計，將時間復雜度降低到O(n)。源域和目標域總樣本MMD在第l卷積層的無偏估計可以表示為：

3.2 基于L-MMD算法的CE-MMD損失函數及推導

定義2針對2.2.1節中傳統交叉熵函數存在的不足，提出一種新的損失函數CE-MMD，即在反向傳播過程中添加L-MMD正則項，將殘差δ和兩個域樣本間的分布差異共同作為更新網絡參數的指標，在迭代訓練中CE-MMD 損失值不斷減小的同時模型趨于收斂。改進后的CE-MMD損失函數定義為：

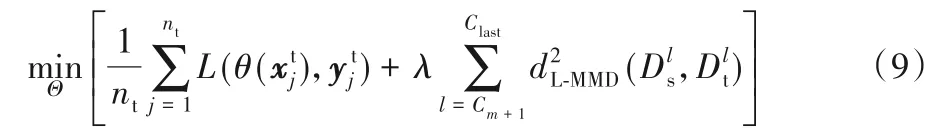
其中λ是懲罰因子。

根據最大均值差異嵌入（Maximum Mean Discrepancy Embedding，MMDE）［19］，可以將改進后的簡化成：

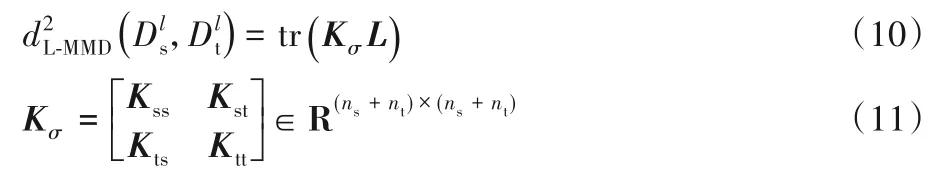
其中Kss、Ktt和Kst(Kts)分別是源域、目標域和跨域的核矩陣。核矩陣KσL 是維度為(ns+nt)×(ns+nt)的半正定矩陣。

由于L-MMD核嵌入算法的時間復雜度為O(n)，導致核矩陣K 中出現大量的0，稀疏性降低了計算的復雜度，但同時容易出現奇異矩陣，使得K的逆矩陣無法計算，最終導致誤差反向傳播的過程中網絡參數無法更新。為了減少此現象發生，將K 加上一個同樣維度的單位矩陣I，最終核矩陣調整為K=

證明 下面推導CE-MMD損失函數在反向傳播中更新參數的過程，以一個mini-batch 在T-typCNNs 中的隨機梯度下降（Stochastic Gradient Descent，SGD）為例：

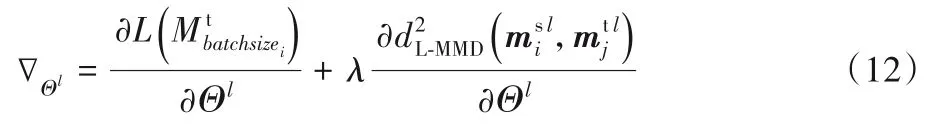
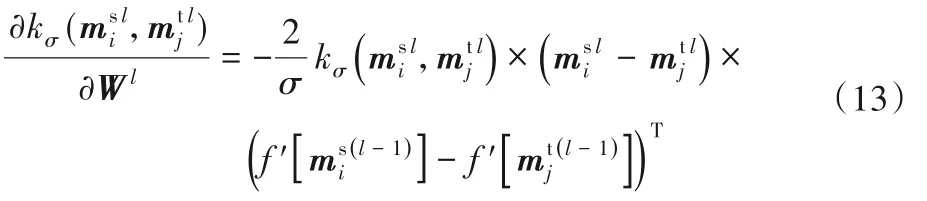
其中：f 是T-typCNNs 的激活函數ReLU，fl(x)=max(0，x)，所以當

4 實驗與分析

本文實驗環境為Windows 10 操作系統，CPU intel Xeon X5650 2.67 GHz，內存為16 GB，實驗基于Tensorflow 的Keras框架。實驗主要包括3個部分：

1）為證明所提出的MCA 深度遷移框架對臺風等級分類的實用性，將基于MCA 框架的T-typCNNs 模型性能與原始T-typCNNs模型作對比；

2）對CE-MMD 損失函數中的參數（懲罰因子λ 和單位矩陣系數α）取值作探討，分析參數靈敏度對模型性能的影響；

3）為證明L-MMD 算法的可行性，將L-MMD 算法與應用廣泛的度量算法Bregman 差異［20］和KL（Kullback-Leibler）散度［21］作對比。

4.1 數據集構建

本文所構建的目標域樣本由日本國立情報學研究所（National Institute of Informatics，NII）提 供，取 自“GMS-5”“GOES-9”“MTSAT-1R/-2”和“Himawari-8”多個氣象衛星在西北太平洋上空拍攝的10 000多景高分辨率臺風云圖。依照國際臺風分類標準，根據臺風中心風速將紅外云圖分為5 類：熱帶低壓、熱帶風暴、強熱帶風暴、臺風和強臺風，如表1所示。

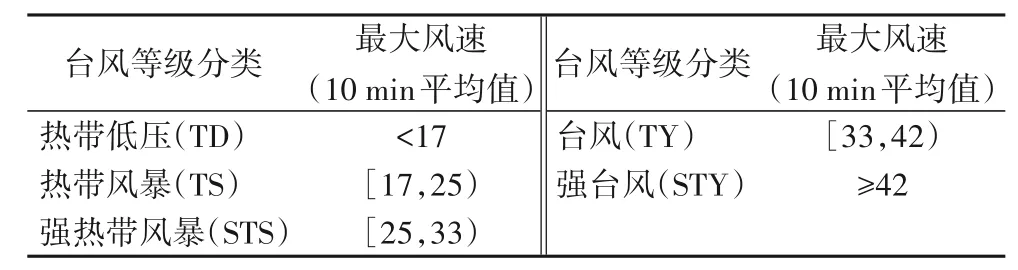
表1 臺風等級標準 單位：m·s-1Tab.1 Typhoon grade standards unit：m·s-1

臺風云圖數據集采用5 類標簽標記，每類圖像2 500 張，總樣本12 500 張。其中10 000 張為訓練集，占20%；2 500 張為測試集，部分云圖樣本如圖2所示。由于T-typCNNs模型輸入為224×224 分辨率的三通道圖像，本文首先對氣象云圖重采樣，然后將單通道灰度圖像擴增成RGB 三通道。為減少兩域樣本數量及內容的差異引發的過擬合問題，對圖像進行增強和歸一化處理，通過隨機旋轉、縮放、偏移和翻轉等進行數據擴增。

圖2 臺風數據集部分樣本Fig.2 Samples of typhoon datasets

Yosinski 等［12］依據類別標簽的語義信息，將ImageNet 數據集中1 000 個類別的100 多萬張彩色圖像平均劃分成兩個子數據集，即449 類的自然圖片（ImageNet-449）和551 類的人造圖片（ImageNet-551）。由于MCA 深度遷移框架以TtypCNNs 模型為基礎，該模型遷移的ResNet50 網絡是在ImageNet 數據集上建立的，所以本文在ImageNet-449 和ImageNet-551 子數據集中每類隨機抽取50 張圖片，最終分別構建了22 450和27 550個源域樣本。

4.2 基于MCA深度遷移框架的臺風等級分類

實驗將臺風數據集的批數量batchsize 設置為64，源域數據集ImageNet-499 和ImageNet-551 的批數量batchsize 分別 設置為143 和176，以確保兩域樣本的遍歷次數相同。采用隨機梯度下降法，微調自適應卷積層的超參數設置：學習率為1E -4，學習動量為0.9。CE-MMD 函數中帶寬參數σ 采取中值規則、懲罰因子λ=1.5、單位矩陣I 的系數α=1。將基于MCA 深度遷移框架的模型與T-typCNNs 對比，在臺風數據集上迭代200次后的測試精度如圖3所示。

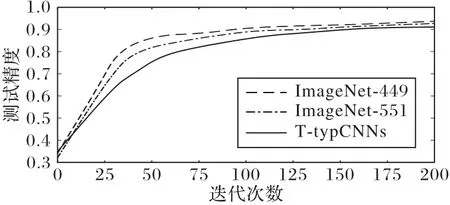
圖3 MCA深度遷移模型與T-typCNNs測試精度對比Fig.3 Test accuracy comparison of MCA deep transfer model and T-typCNNs

從圖3 可以看出，基于MCA 深度遷移框架的模型在源域ImageNet-449 或ImageNet-551 上分別在迭代32 次和41 次后均趨于穩定，測試精度達到93.68%和92.73%，比T-typCNNs模型平均提高了2.55 個百分點，且收斂速度更快。分析原因，T-typCNNs 模型在凍結前110 層后，剩余卷積層參數利用殘差在臺風數據集上作自適應調整。然而該模型遷移的是ResNet50 整體網絡結構，剩余卷積層間存在脆弱的互適應性影響了遷移效果。針對此問題，MCA 深度遷移框架中CEMMD 損失函數在殘差反向傳播的過程中，添加了L-MMD 正則項，在減少兩域分布差異的同時提高了T-typCNNs 模型在臺風數據集上的適配程度。表2將基于MCA深度遷移框架分別與T-typCNNs、文獻［18］中自建的淺層卷積神經網絡CNN_8、InceptionV3、VGG16 模型在凍結最佳遷移層參數后的訓練和測試精度進行對比。

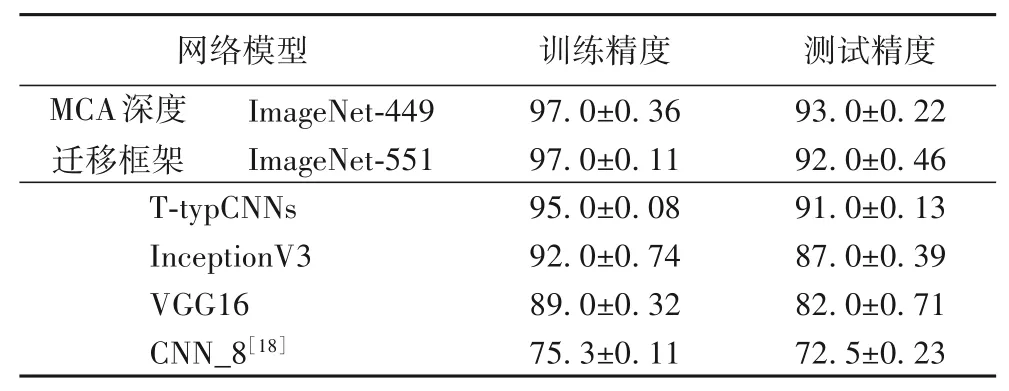
表2 MCA深度遷移網絡模型和其他模型的性能對比單位：%Tab.2 Model performance comparison of MCA deep transfer network models and other models unit：%

4.2.1 參數靈敏度分析

CE-MMD 損失函數中存在兩個參數，分別是懲罰因子λ和單位矩陣系數α。實驗將研究λ 和α 的取值對模型性能的影響。以ImageNet-449 源域樣本為例，圖4（a）刻畫了當λ ∈{0.5，0.7，1，1.3，1.5，1.7，2，2.5，3}對模型分類精度的影響；圖4（b）展示了當α ∈{0.5，1，1.5，2，2.5}時，模型的準確率變化，其余各訓練參數不變。

由圖4（a）可見，CE-MMD 函數對懲罰因子λ 靈敏度較高，當λ=1.5 時，模型取得最佳分類精度93.22%，λ 過小或者過大，精度均有所下降，波動振幅在3.1 個百分點。由于懲罰因子決定了兩域的融合程度，如果λ 太小，L-MMD 正則項沒有約束作用，導致適配效果不佳；如果λ 太大，兩域的樣本點在RKHS 中的距離太近，使得模型學習到了退化的特征表示［20］，一定程度上影響模型性能。從圖4（b）可以看出，當λ 取固定值后，單位矩陣系數α對模型精度的靈敏度不高，波動振幅在0.1個百分點。

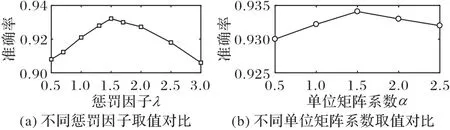
圖4 參數λ和α的靈敏度分析Fig.4 Sensitivity analysis of parameters λand α

4.2.2 L-MMD度量算法及對比實驗

為了驗證L-MMD 算法的可行性，將其他應用廣泛的度量算法Breman 差異、KL 散度作為交叉熵損失函數的添加正則項，與CE-MMD函數進行對比，其他訓練參數不變。

由圖5 可見，模型使用L-MMD 作為正則項的CE-MMD 損失函數，在訓練時收斂速度最快且獲得最小損失值0.047，而Bregman 差異和KL 散度作為度量算法時訓練出的模型性能均不佳。對照表3，使用L-MMD 算法的模型訓練精度高達93.22%，訓練精度均比其余算法提高大約11.76 個百分點和8.05個百分點。分析原因，雖然Bregman 差異和KL 散度都是經典的度量方法，但計算的是一種信息損失/增益，不適用于在線學習模型。在一個批數量batchsize中的樣本數量有限的前提下，利用Bregman 差異和KL 散度度量并不準確。L-MMD算法適用于處理服從某種概率分布下的數據分布差異，能直觀地反映樣本總體的分布信息和全局結構信息，計算簡單有效。在獲得更高模型精度的同時，L-MMD 算法單次迭代的訓練時間比傳統MMD 算法節省約89 s，充分證明了該算法的可行性。

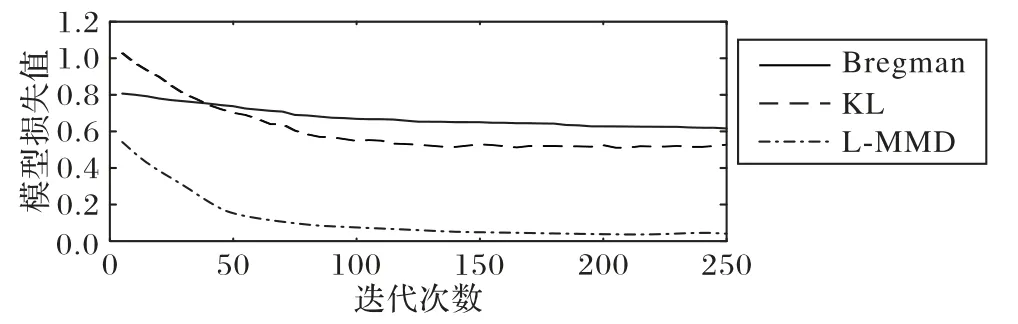
圖5 不同度量算法的模型損失值對比Fig.5 Comparison of model loss values of different measurement algorithms

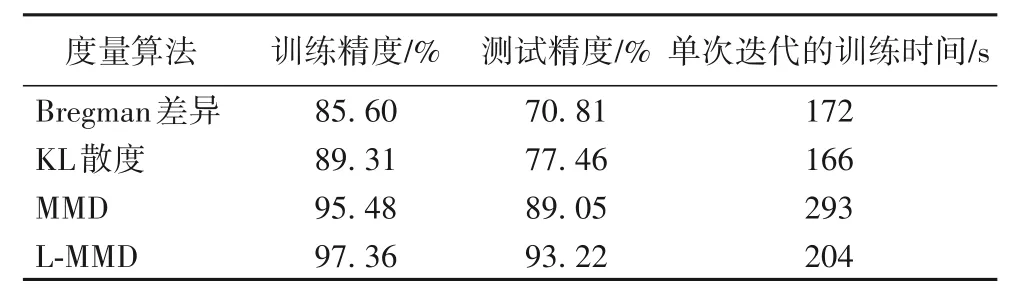
表3 不同度量算法模型的性能對比Tab.3 Performance comparison of different measurement algorithms

5 結語

本文提出了一種MCA 深度遷移框架，遷移DCNN 整體網絡結構并凍結部分卷積層參數不更新，剩余自適應層參數依據源域和目標域樣本的分布差異進行多層領域適配，緩解了卷積層間脆弱的互適應性對模型遷移性能的影響，并成功提高了氣象領域小樣本臺風數據等級分類模型的性能。對于MCA深度遷移框架，有以下兩點總結：

1）基于L-MMD 算法的CE-MMD 損失函數：L-MMD 算法是度量概率分布差異的準則，CE-MMD 函數將L-MMD 算法作為正則項添加到交叉熵損失函數中，在殘差反向傳播的過程中使得模型收斂速度更快，精度更高。與傳統的MMD算法時間復雜度O(n2)相比，L-MMD 將時間復雜度減小到了O(n)。基于MCA深度遷移框架的T-typCNNs臺風等級分類模型的訓練精度可達97.36%，測試精度可達93.22%，同比原始T-typCNNs 模型的精度提高了2.27 個百分點和2.08 個百分點，比凍結最佳遷移層數后的InceptionV3和VGG16模型的測試精度高出5.83個百分點和10.51個百分點。

2）為了驗證MCA 深度遷移框架的可行性，對CE-MMD 損失函數中的兩個參數：懲罰因子λ 和單位矩陣系數α 作了靈敏度分析，并將L-MMD 算法其他度量算法Bregman 差異、KL散度、傳統MMD 算法作對比。實驗表明，MCA 框架中的CEMMD函數收斂最快，且模型準確率比Bregman差異和KL散度高出11.76 個百分點和8.05 個百分點。L-MMD 算法在模型單次迭代的訓練時間比傳統MMD算法節省89 s。

在MCA 深度遷移框架中，CE-MMD 損失函數中的懲罰因子在本文中設置為固定值，如何依據L-MMD 正則項計算出的兩域分布差異，對每一層懲罰因子λ 的取值做自適應調整是下一步研究的重點。