船舶進出船廂下沉量預測

傅陸志丹， 胡亞安

(南京水利科學研究院， 通航建筑物建設技術交通行業重點實驗室， 江蘇 南京210029)

升船機作為耗水少、 運行速度快的通航建筑物對實現內河航運的通暢起著不可或缺的作用，我國至今已先后建成清江隔河巖、 清江高壩洲、紅水河巖灘、 閩江水口、 烏江思林、 沙沱等鋼絲繩卷揚垂直升船機， 長江三峽、 金沙江向家壩齒輪齒條爬升式升船機以及瀾滄江景洪水力式升船機等多座大型升船機。 此外還有烏江構皮灘、 紅水河龍灘和巖灘、 右江百色等多座垂直升船機正在設計建設中[1]。

升船機在空中運行階段通常流程簡單、 平穩順暢。 而升船機船廂與上下游對接船舶進出船廂階段， 由于承船廂一般采用廂形結構形式， 為了降低升船機的拖動功率并減少工程造價， 設計確定的船廂斷面系數較小， 一般僅為2.0[2]。 由于承船廂尺寸限制， 船進出的運動過程中， 淺水效應和岸壁效應對船舶水動力有顯著影響， 導致該階段升船機運行流程較為復雜、 影響因素眾多， 是升船機安全運行核心環節之一。 為準確判斷船舶進出船廂的航行下沉量， 科學合理制定船舶吃水控制標準， 提高升船機安全運行和通過能力， 本文對船舶進出升船機船廂下沉量研究進行了總結，并提出今后的研究方向和內容。

1 船舶進出船廂航行特性

國際上普遍按照航道斷面形式將航道分為3 類:非限制性航道、 挖槽式航道和限制性航道[3]。當船舶航行在無限深廣的水域， 如海洋、 深水湖泊、 高水頭樞紐工程的庫區航道等， 斷面系數趨于無窮大， 船舶航行過程中不存在阻塞效應， 船身周圍的回流現象較限制性航道要小得多， 船體下沉也遠小于限制性航道。

當船舶在挖槽式航道中航行時， 如一般內河航道、 進港港區航道、 淺海航道等， 斷面系數主要受水深、 吃水比影響， 淺水效應對船舶航行產生諸多影響[4]， 船體下沉及縱傾加劇。

限制性航道定義是因水面狹窄、 斷面系數小而對船舶航行有明顯限制作用的航道， 如運河、 渠道和河網地區的部分航道等。 與在非限制性航道航行有所不同， 流經船體的水流由于在空間上受到限制， 流態由在無限水域中的三維空間流動變為船體兩側的二維平面流動， 從而導致船體周圍水壓力的分布發生改變， 船舶阻力增加， 船體表面的水動力的大小和分布發生變化。 為了使船體受到的重力與浮力重新達到平衡， 船體就要在水中發生垂直方向上的移動， 這就是船舶的下沉[5]， 見圖1。

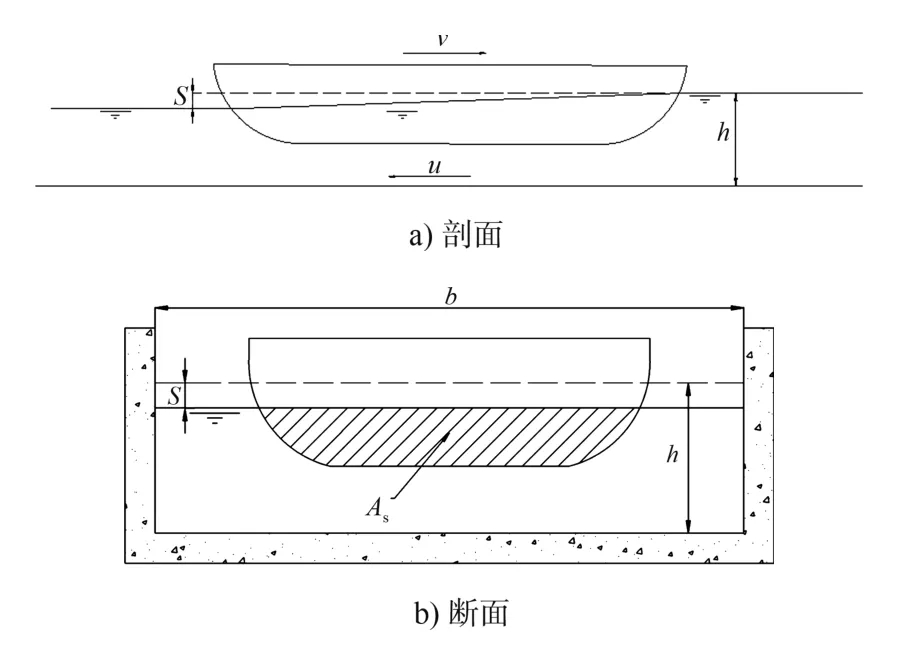
圖1 船舶下沉現象概化

船舶進出船廂的過程可以看成是船舶在既窄又淺的特殊限制性航道中行駛[6-7]， 見圖2。 從外部水域條件分析， 相比進港航道和運河， 升船機船廂水域限制性更強、 水域有效過水斷面更小，斷面系數在1.6～2.0， 這會增加船舶航行下沉量。而且由于船廂的半封閉性， 在船舶進入船廂的過程中， 船舶對船廂水體的擾動與推進作用將會在船廂內部形成推進波系， 該波系在推進到船廂頂端的時候會與頂端廂壁發生固-壁反射現象， 并在船廂連接引航道的限制性水域內形成反射疊加波，進而造成船舶運動(下沉、縱傾、偏艏)的復雜性。因此， 須對船舶進出船廂下沉量進行專門研究。

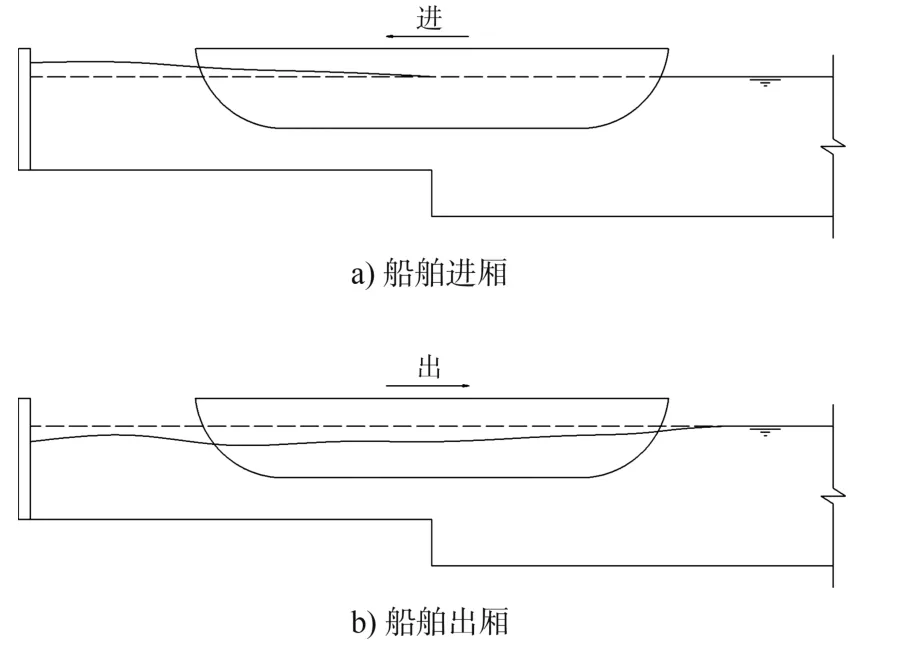
圖2 船舶進出船廂示意

2 船舶進出船廂下沉量主要影響因素

經過前人的研究， 影響船體下沉量的主要因素得到初步歸納。 JTJ 211—1999 《海港總平面設計規范》在確定航行下沉量時， 考慮了船舶載質量和航速兩個因素； 國際航運協會(PIANC)《進港航道設計導則》推薦的公式中除考慮船舶載質量和航速兩個因素外， 還考慮了水深、 斷面系數和斷面形狀以及船舶類型的影響； 美國陸軍工程師團《深水航道水力設計》推薦的航行下沉量計算公式考慮了船舶載質量、 船舶航速、 船舶方形系數、 船舶吃水和航道水深； 南京水利科學院對船舶進出船廂過程中下沉量的影響因素進行研究分析后得出主要影響因素為: 船舶航行方向、 船舶航速、 船廂水深和斷面系數， 其中斷面系數為航道過水斷面面積與船舶過水斷面面積之比。

綜上， 影響船舶進出船廂下沉量主要因素有:1)船舶尺度； 2)船舶吃水； 3)船舶航速； 4)船廂尺度； 5)船廂水深； 6)船舶方型系數。

3 下沉量計算方法

已有不少學者對船舶下沉量計算進行了相關研究[8-13]， 主要研究方法包含了3 大塊: 理論分析、 物理模型試驗和數值模擬， 但以理論分析和模型試驗居多， 通過長期的研究， 形成了一系列船舶下沉量預測公式。

3.1 國際航運協會的《進港航道設計導則》中推薦的3 種下沉量計算公式

3.1.1 Barrass 公式

1981 年， Barrass[14]分析了在開敞水域和限制性航道不同船型(0.5≤Cb≤0.9)船舶的航行下沉量模型試驗結果， 給出了船首下沉量的計算公式，其計算結果為平均下沉量:

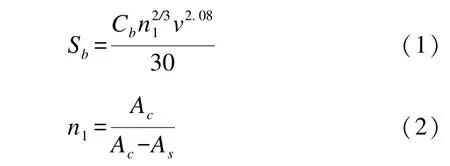
式中: Sb為船首下沉量； Cb為船舶方形系數；n1為斷面系數； v 為船舶航速； Ac為航道過水斷面面積； As為船舶過水斷面面積。 南京水利科學研究院的研究表明， 船舶進出升船機船廂過程中，船尾發生的下沉量往往大于船首發生的下沉量，Barrass由于沒有考慮縱傾變化， 計算數值偏大。

2009 年， Barrass 在《船舶航行下沉及相互影響》[15]一書中對船舶航行下沉量進行了系統的分析。 并對其1979 年提出的公式進行了修改。 新的公式適用于開敞水域和限制性航道， 其使用范圍為: 1.1≤h∕T≤1.4， 4≤n≤10， 0.5≤Cb≤0.85，0≤v≤10.3 m∕s， 并不適用于升船機船廂中船舶下沉量的計算。

式中: S 為船舶下沉量； Cb為船舶方形系數； n 為斷面系數， n=Ac∕As； v 為船舶航速； h 為航道水深； T 為船舶吃水。

3.1.2 Eryuzlu 公式

1978 年Eryuzlu 和Hausser[16]在橫向無限水域和有限水深航道中進行了3 艘自行式超大型油輪(VLCC)模型試驗， 發現了船舶下沉、 船速和吃水之間的關系， 得出了以其名字命名的經驗公式， 和Barrass公式一樣， Eryuzlu 給出的是船首下沉量的計算公式， 同時沒有考慮阻塞效應對下沉量的影響。

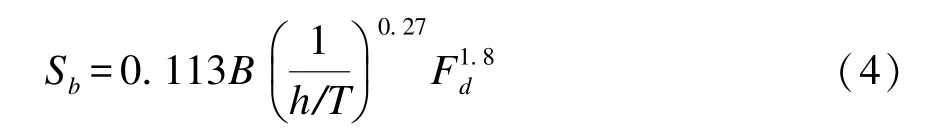
式中: Sb為船首下沉量； B 為船舶寬度； h 為航道水深； T 為船舶吃水； Fd為水深弗勞德數， Fd=

3.1.3 Huuska∕Guliev 公式

1976 年， Huuska[17]引入阻塞系數這一概念，并提出寬度受限水域中船舶下沉量估算公式， 其適用于無限水域航道、 限制性航道和運河， 但是不能應用于水深弗勞德數大于0.7 的情況， 且僅給出了船首最大下沉量的計算公式:

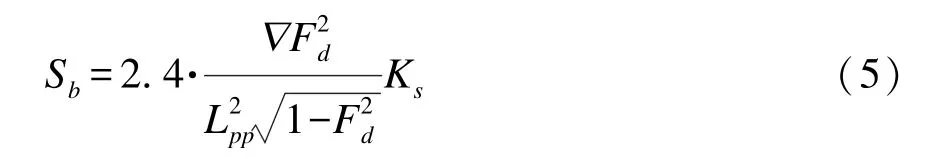
式中: Sb為船首下沉量； ?為船舶排量； Fd為水深弗勞德數； Lpp為船舶兩柱間長； 修正系數Ks取值如下:

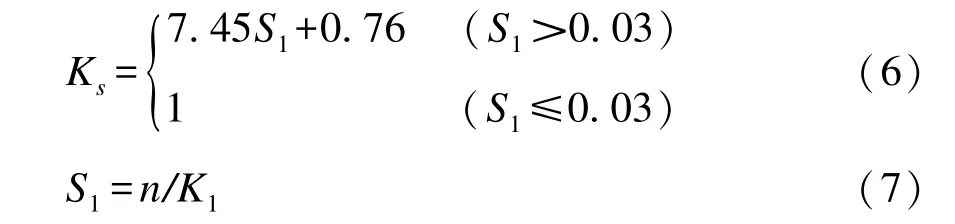
式中: K1為修正系數， 可通過圖3 得出； n 為斷面系數。 除此以外還有許多下沉量計算經驗公式，主 要 包 括: Tuck 公 式[18]、 Romisch 公 式[19]、Millward 公式[20]、 Ankudinov 公式[21]、 ICORELS 公式[22]、 Yoshimura 公式、 Norrbin 公式[23]等， 這些公式都具有一定的適用范圍和條件， 見表1。

圖3 修正系數K1

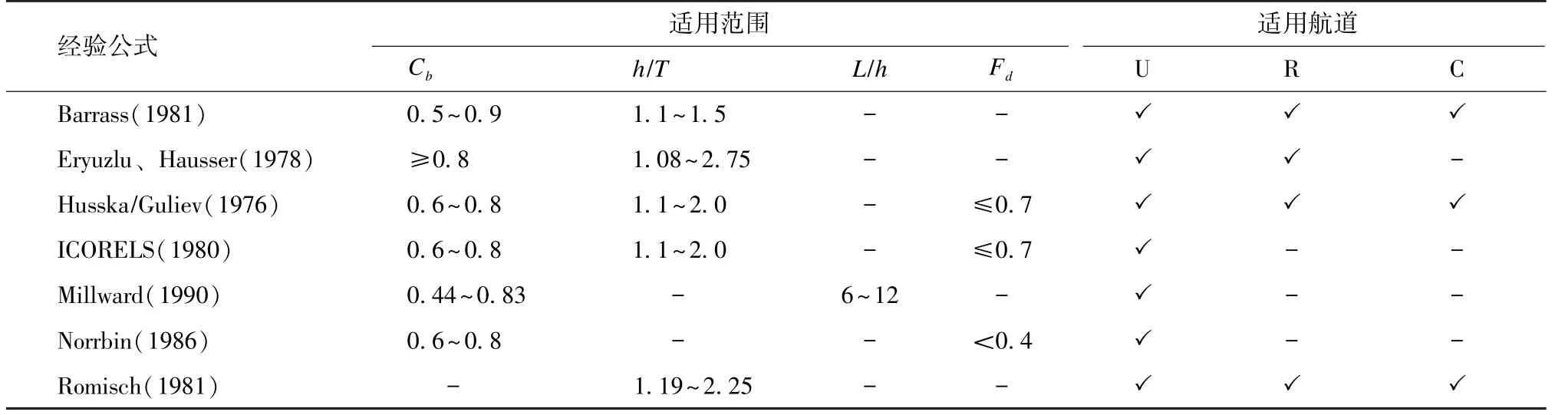
表1 常用經驗公式使用條件

3.2 船舶進出升船機船廂下沉量計算方法

3.2.1 我國《升船機設計規范》公式

在GB 51177—2016 《升船機設計規范》條文說明中， 關于船舶進出廂下沉量推薦采用包綱鑒[24]于1991 年提出的經驗公式， 該公式基于三峽、 陸水、大化等升船機的模型試驗資料擬合得到:

式中: S 為下沉量； Fd為水深弗勞德數； n 為斷面系數； T 為船舶吃水。

3.2.2 NHRI 下沉量經驗公式

2011 年， 胡亞安等[25]為分析船舶下沉量的主要影響因素， 假定船舶在狹淺無限長區域航行，根據圖1， 將坐標系固定在船舶上建立了以下方程組:

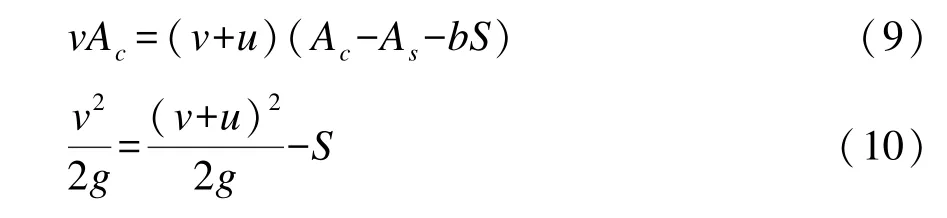
式中: v 為船舶航速； u 為船舶周圍水流回流速度； Ac為航道過水斷面面積； As為船舶過水斷面面積； b 為航道寬度； S 為下沉量。

將三峽、 向家壩、 思林、 構皮灘[26]等升船機岀廂過程下沉量S、 船速v、 船廂水深h 和斷面系數n 等變量通過無量綱處理后， 繪制的P-K 關系曲線見圖4， 其中從圖4 可以看出， 船舶航行下沉量與水深弗勞德數成二次函數關系， 由此提出了物理意義更為明確的NHRI 下沉量經驗公式:

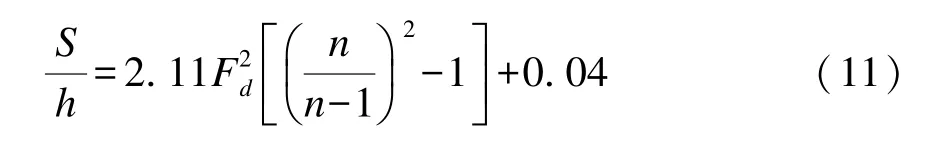
圖4 不同升船機下沉量關系曲線

該公式的優點在于直接獲取船舶下沉量， 經過最小二乘法擬合出的經驗公式對符合試驗條件的船舶下沉量預測精度高。 但是由于船模試驗需要預先建造船模設置試驗條件， 每進行一組試驗耗資巨大且費時； 且每座升船機P-K 關系中斜率的取值沒有得到規律性的總結， 限制了該公式的適用范圍。

3.2.3 德國呂內堡升船機模型試驗公式

2005 年， 德國聯邦航道設計研究院針對現代大型內河船舶進出呂內堡升船機的問題開展了研究工作。 航行試驗中發現船舶駛出升船機的速度受到阻塞系數的限制， 在航行試驗中， 還對升船機上游側非恒定流波動的水位進行了觀測， 并對試驗結果進行分析， 提出船舶出廂時最大航行下沉量的計算公式:

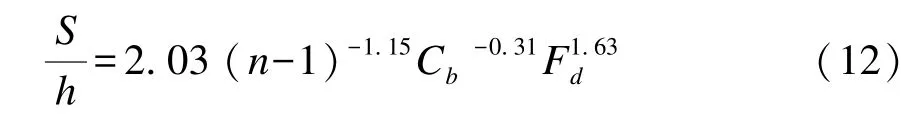
式中: S 為下沉量； h 為航道水深； n 為斷面系數； Cb為船舶方形系數； Fd為水深弗洛德數。 該公式適應范圍為: 1.17≤n≤3.26、 0.018≤Fd≤3.26、 0.83≤Cb≤0.96。

4 下沉量經驗公式對比分析

以我國三峽升船機船舶出廂試驗為例， 由于Barrass 公式斷面系數適用范圍在4 ～10， 故采用國際航運協會的《進港航道設計導則》中推薦的Eryuzlu 公式、 Huuska∕Guliev 公式以及我國《升船機設計規范》公式、 NHRI 公式和德國呂內堡升船機模型試驗公式， 分析船舶航行下沉量計算結果， 與物理模型實測值對比結果見圖5。 可以看出， 幾種公式計算結果與實測值趨勢一致， 其中Eryuzlu 公 式 計 算 結 果 偏 大， Huuska∕Guliev 公 式和我國《升船機設計規范》公式計算結果偏小，而NHRI 公式和德國呂內堡升船機模型試驗公式與實測值吻合較好。 特別是當航速超過0.7m∕s，Eryuzlu 和Huuska∕Guliev 公式的計算結果與實測值誤差更大。 因此， 當前國際航運協會推薦的3 種下沉量計算公式并不適用于我國升船機等通航建筑物的下沉量計算。

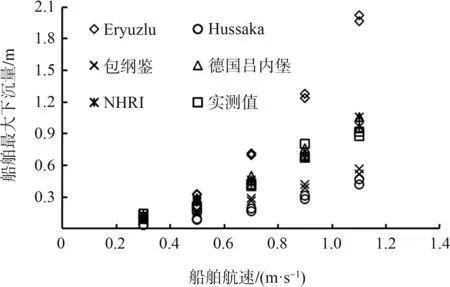
圖5 不同計算方法計算船舶的航行下沉量對比

雖然NHRI 公式和德國呂內堡升船機模型試驗公式與物理模型實測值吻合較好， 但在近期南京水利科學研究院船舶出廂下沉量影響因子試驗研究[27]中發現， 在斷面系數一樣的情況下， 船廂過水斷面存在不同組合的寬深比， 同一出廂航速下， 船舶下沉量也有一定差異， 見圖6。 以上兩個公式都沒有考慮到這一情況，且歐洲船型與國內船型尺度有所不同， 針對我國升船機等通航建筑物， NHRI 公式還須進一步考慮船型對下沉量的影響。 同時， 當前研究均沒有考慮船廂長度、 船舶在船廂中停泊位置以及船舶啟動加速度對下沉量的影響， 這些因素也有待進行初步探討。

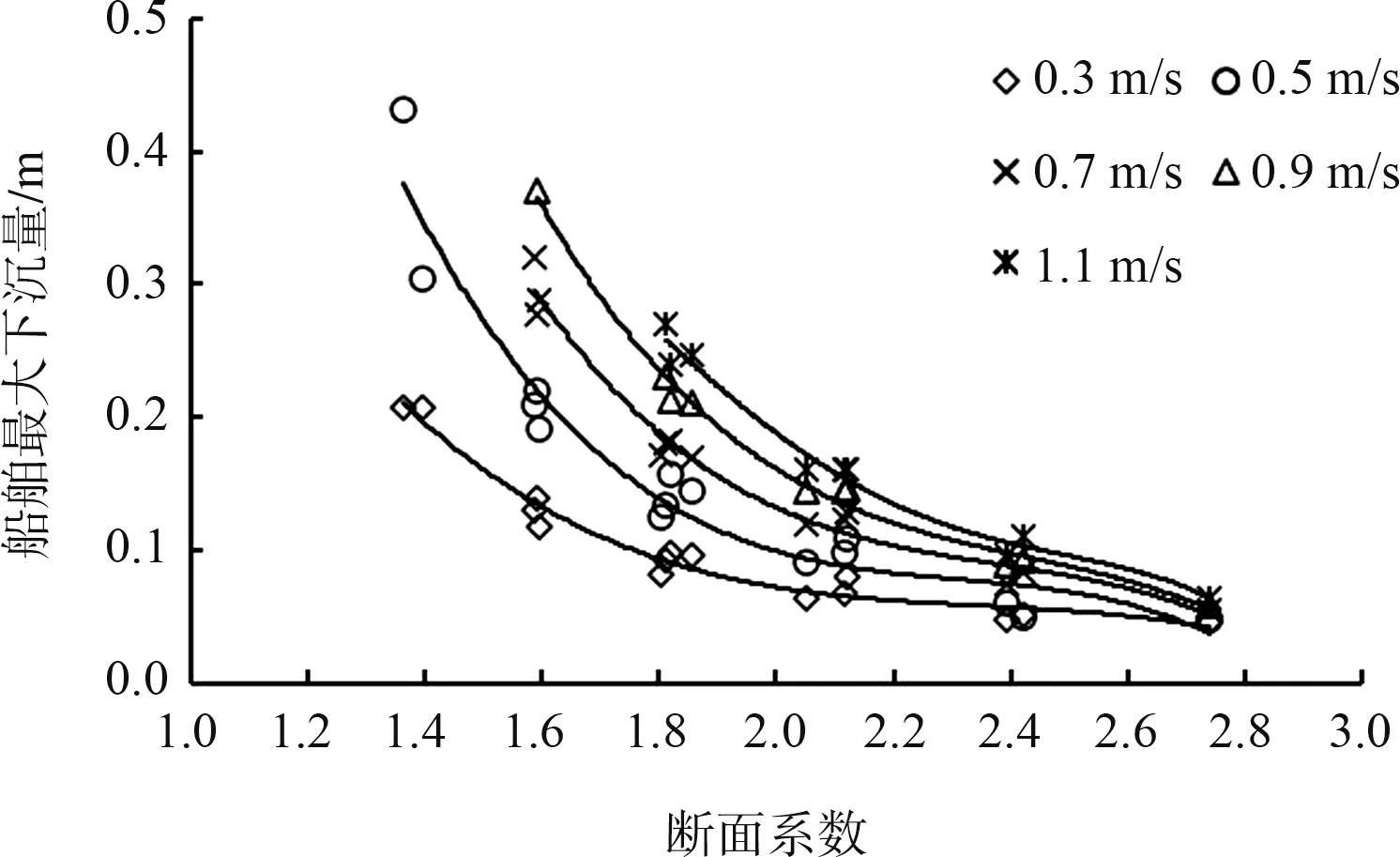
圖6 不同航速下船舶出廂斷面系數與最大下沉量的關系

5 結語

1)與非限制性水域不同， 升船機船廂外部水域條件和船廂的半封閉性都會導致船舶運動的復雜性， 須對進出船廂船舶的下沉量進行專門研究，主要影響因素有: 船舶尺度、 船舶吃水、 船舶航速、 船廂尺度、 船廂水深和船舶方型系數。

2)目前國內外已有一系列的下沉量計算公式，但現有計算方法大多是針對船舶在無限水域或是進港航道、 運河中的船舶航行下沉量， 且有較為復雜和嚴格的約束條件。

3)對于升船機船廂這一特殊限制性航道， 雖然已有與實測值吻合較好的經驗公式， 仍有相關問題有待進一步深化研究。 尚須對斷面系數相同、船廂不同寬深組合對下沉量的影響進行研究， 同時在已有公式中， 補充船型對下沉量的影響。 有待研究船廂長度、 船舶在船廂中停泊位置以及船舶啟動加速度等因素對下沉量的影響。