近場水下爆炸氣泡與雙層破口結構的相互作用*

賀 銘，張阿漫，劉云龍

（哈爾濱工程大學船舶工程學院，黑龍江 哈爾濱 150001）

在船舶與海洋工程領域，爆炸[1-6]問題具有極其重要的研究意義。隨著水下高技術武器的發展，艦船和潛艇等海洋裝備的安全受到越來越嚴峻的挑戰，水下爆炸[7-11]對海洋裝備造成的結構毀傷十分嚴重。因此，研究艦艇在水下爆炸作用下的毀傷特性十分必要，掌握不同邊界條件下的艦艇毀傷機理對提高現代海軍的作戰能力具有重要意義。

水下爆炸載荷作用較為復雜，主要分為瞬態的沖擊波載荷和脈動的氣泡載荷。對于近場水下爆炸，高強度的瞬態沖擊波會造成結構的塑性破壞，氣泡的脈動將會進一步造成艙室涌流以及結構的全局破壞。從水下爆炸載荷的作用機理出發，沖擊波過后會形成氣泡和不完整邊界的耦合作用，科學家們在該問題上進行了很多研究。劉云龍等[12]對背空船底板在氣泡載荷下的破壞機理進行了研究，劉念念等[13]對有限水域破口問題進行了研究，劉潤泉等[14]進行了艦船單元結構模型水下接觸爆炸破口的實驗研究，李金河等[15]通過實驗分析了近場沖擊波的傳播規律，楊棣等[16]對接觸爆炸載荷作用下船體板架破口大小進行了預測。對于復雜邊界條件下的水下爆炸問題來說，理論解的獲得是極其困難的，而實驗研究[11,14-15]又會花費大量的人力物力，所以介紹實尺寸實驗的文獻特別少。隨著計算機技術的不斷發展，數值模擬方法[17-18]逐漸成為研究水下爆炸破壞機理及艦艇結構抗沖擊性能的有效工具，其中邊界積分方法[19]、有限體積方法[20]和耦合歐拉-拉格朗日方法[21]等廣泛應用于水下爆炸問題的模擬。

本文中基于歐拉有限元方法對近場水下爆炸氣泡與雙層破口結構的相互作用機理進行研究。通過實驗驗證歐拉有限元理論數值模型的準確性，通過氣泡形態、流場壓力、艙室進水量等參數對不同破口尺寸、不同起爆位置和不同殼間水位條件下的水下爆炸過程進行系統分析。

1 問題描述

對于裝備雙層外殼的艦艇結構，當沖擊波載荷將雙層外殼破壞后，其內部結構會受到因氣泡和復雜不完整邊界的耦合作用產生的水射流和涌流的沖擊，而由于破口結構的卸載作用，涌流效應更加明顯，高速涌流會對內層殼結構造成毀傷，其作用過程本質上是近場水下爆炸氣泡與雙層破口結構的相互作用問題，如圖1 所示。

圖1 近場水下爆炸氣泡與雙層破口結構相互作用示意圖Fig. 1 Schematic of interaction between bubble and double breaken structure in near field underwater explosion

2 理論數值模型

2.1 可壓縮歐拉有限元

為了在保證求解精度的前提下提高數值模擬的求解效率，將復雜的工程問題簡化為軸對稱的數值模型。可壓縮歐拉有限元方法[22-24]在處理流體瞬態大變形問題中具有明顯的優勢，如圖2 所示。忽略黏性項，在求解過程中每個單元的控制方程如下：

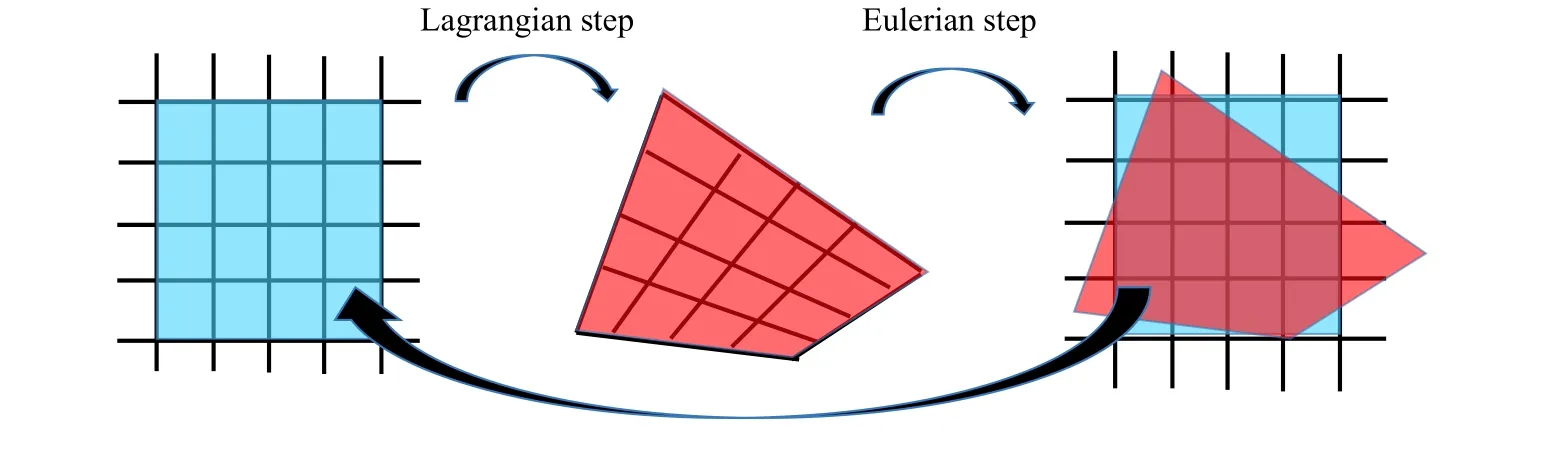
圖2 歐拉有限元方法示意圖Fig. 2 Schematic of Eulerian finite element method

此時每個計算時間步的拉格朗日過程處理完畢，歐拉的計算步驟開始執行。本文中歐拉有限元主要通過體積分數法和單調迎風輸運格式確定單元之間的輸運量，進而完成動量等變量的更新。下一個計算步的初始壓力等變量則通過狀態方程進行更新。拉格朗日計算步和歐拉計算的反復迭代，實現了復雜問題的求解。另外，本文中選擇Tammann 方程[25]作為水和空氣的狀態方程，即：

2.2 相關參數與無量綱處理

3 實驗驗證

利用氣泡放電實驗對所建立的水下爆炸數值模型進行驗證。針對所研究的問題，本文選擇氣泡與自由液面及破口平板相互作用的實驗工況進行對比驗證。實驗在50 cm×50 cm×50 cm的水箱內完成，其中氣泡由220 V 高壓放電產生，高速攝像機用于拍攝整個實驗過程，具體的實驗操作可參考文獻[11]，實驗裝置如圖3 所示。另外，帶有30.0 mm 破口的2.0 mm 厚平板放置于靜止水面，氣泡初始位置距離水面12.0 mm，氣泡最大半徑12.6 mm。圖4 為不同時刻的數值結果與實驗結果對比圖。

圖3 實驗裝置圖Fig. 3 Picture of experimental device

圖4 數值結果和實驗結果的對比圖Fig. 4 The comparison between numerical and experimental results

在數值模擬中，計算模型與實驗模型中破口尺寸、板厚等基本參數一致。另外，計算域尺寸為0.15 m×0.05 m，最小網格尺寸為2.5×10－4m，計算域邊界為數值的無反射邊界[27]。由圖4 可知，數值模擬中的氣泡膨脹、收縮和射流等氣泡形態和水冢現象與實驗現象基本一致。其中，由氣泡能量傳遞所形成的自由面處水冢并誘導結構產生的涌流現象被有效地模擬，其多峰效應也被很好地展示。另外，如圖4(d)所示，本文的數值模擬方法能較好地模擬氣泡運動后期的撕裂破碎和破口附近復雜的自由液面演化等過程。由圖4 可知，量化的涌流高度及氣泡形態典型參數基本一致。綜上所述，本文的數值結果與實驗結果吻合較好，整個氣泡運動過程都被很好地模擬出來，從而驗證了算法的有效性和準確性。下文中將討論近場水下爆炸氣泡與雙層破口結構的相互作用機理。

4 結果討論

4.1 基本物理現象

近場水下爆炸氣泡與雙層破口結構的相互作用是一個復雜的瞬態非線性問題，影響該物理問題的參數較多。本文中以Rm=5.0 m、R*h1=3.0、R*h2=1.5和R*d=0.4 為參考工況分析該物理過程的相關現象，為下文分析多種因素影響提供對比。主要研究該物理過程中流場的動態變化，所以假設破口邊界為剛性邊界。圖5 為不同時刻的氣泡的形態和流場壓力變化圖。

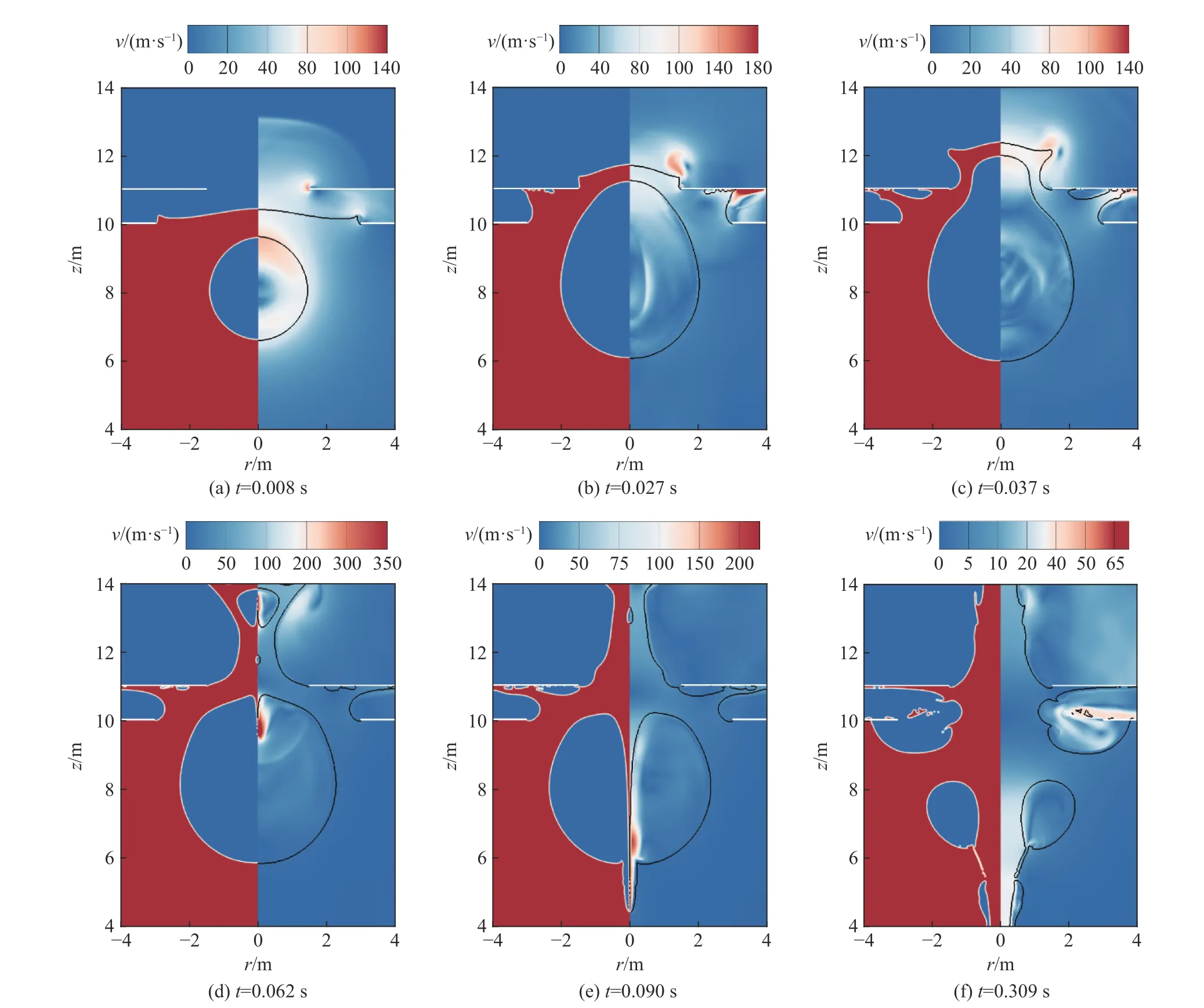
圖5 不同時刻氣泡的形態和流場壓力變化圖Fig. 5 The bubble shape and flow field pressure change at different moments

由于氣泡初始內壓遠大于周圍流場壓力，因此氣泡會迅速膨脹。當t=0.027 s 時，隨著自由液面進一步運動，涌流會超過雙層內殼繼續向內艙室涌入，破口附近空氣流動較劇烈，流速可以達到百米每秒量級。當t=0.037 s 時，可以明顯地看到破口對氣泡形態的影響,氣泡形態開始產生畸變。另外，由于破口的形成，氣泡的運動會帶動自由液面向上運動，進而形成艙室氣泡涌流現象。在艙室進水的過程中，空氣壓縮導致了艙室內空氣的回流。在內部空氣、流體慣性以及破口誘導的聯合作用下，當t=0.062 s時，氣泡演化過程中出現了氣泡分割現象，初始的爆炸氣泡分成了幾個小氣泡和一個較大的主氣泡。在自由液面和破口結構的誘導作用下，當t=0.090 s 時，在氣泡收縮過程中產生了一個遠離自由液面的細長射流，射流穿透氣泡形成環狀氣泡，并進入回彈階段。當t=0.309 s 時，由于流體質點的羽化運動，結構內產生液面飛濺現象。考慮艦艇的生命力，大量的水會隨著氣泡的脈動涌入到破口中，導致結構加速沉沒。

4.2 內外板破口尺寸的影響

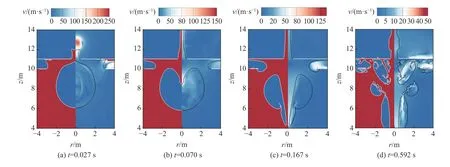
圖6 不同時刻氣泡的形態和流場壓力變化圖Fig. 6 The bubble shape and flow field pressure change at different moments

由圖6 可知，當保持外板破口尺寸不變、只改變內板破口尺寸時，初始階段氣泡及流場運動特性區別不大。而當涌流與內板接觸形成新的邊界條件后，氣泡和流場的運動特性發生明顯改變。相比4.1 節中的工況，R*h2=0.5 時涌流的形態較穩定。當t=0.027 s 時，涌流開始穿過內板破口進入艙室內，涌流尺寸和破口尺寸近似相等，此時自由液面與破口結構之間會形成小的液膜，這是由于空氣壓縮導致的。由流場速度變化圖可以看到，此時內艙室中出現一個較大的高流速區，這是內艙室破口抑制空氣的擴散導致的。當t=0.070 s 時，內艙室破口同時抑制了水的局部流動，氣泡產生了寬射流現象。當t=0.592 s 時，涌流與內板接觸形成新的邊界條件，誘導分離后的氣泡產生進一步破碎，同時內艙室內形成了二次涌流，涌流的形狀呈現“紡錘”狀。總之，破口尺寸對整個流場演化影響很大。

圖7 中對比了三種不同破口尺寸下，總涌流量和內艙室涌流量隨時間的變化情況。由圖7 可知，艙室涌流大致可以分成以下主要階段：初始瞬間急速涌流階段、涌流穩定階段和滯后回落階段。其中，初始急速涌流階段是氣泡膨脹帶動流體的瞬態運動，穩定階段是艙室內的液體在多種因素誘導下達到一個相對動態的平衡狀態，水流回落階段是流體受重力作用后的向下運動。當保證結構外底板尺寸不變時，不同工況下艦艇的總涌流量以及水進入內艙室所花費的時間基本一致。另外，在初始內板破口參數＜1.5 的范圍內，隨著破口尺寸的增大，艙室總涌流量減小，而最終的內艙室涌流量卻變大，這是誘導艦船和潛艇發生沉沒現象的重要原因。由此可知，當破口產生后，破口尺寸越大其受涌流進水的影響越明顯，提高內層殼的結構強度能充分地提高艦艇抗沖擊的能力。

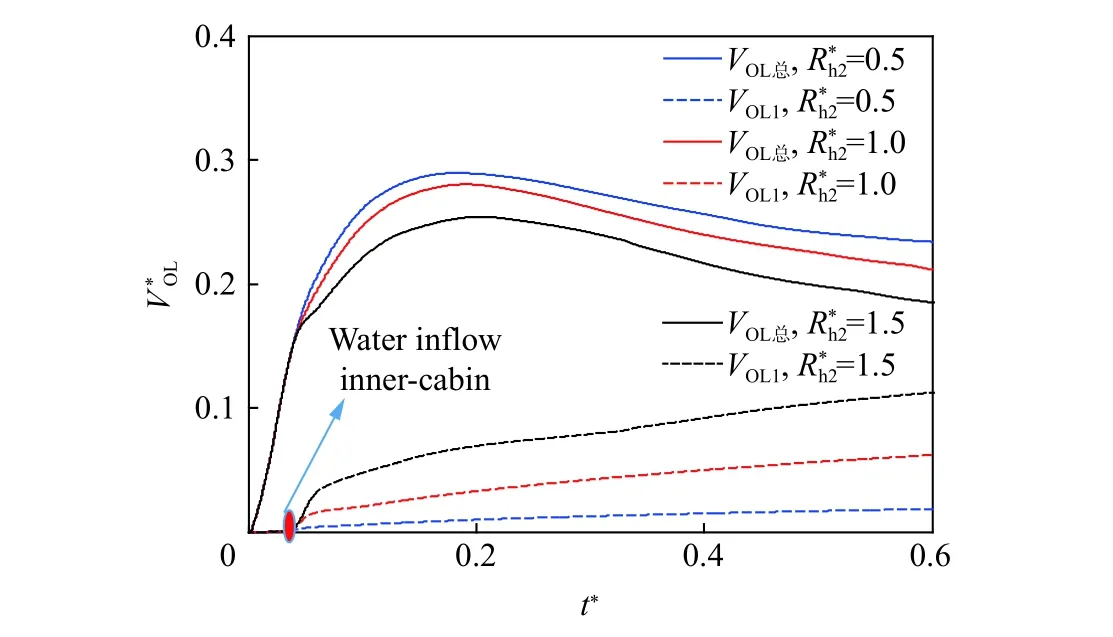
圖7 不同破口尺寸下艙室涌流量隨時間的變化曲線Fig. 7 Changes of cabin inrush flow with time under different breach size

4.3 炸藥起爆初始位置的影響

水中武器對艦艇進行攻擊時，炸藥的起爆位置并不相同。起爆位置距離結構越近，氣泡和復雜邊界的耦合作用越明顯，氣泡后期運動及涌流特性越復雜。本文中選擇R*d=0.1 ， 0 .2 ， 0 .4 分別進行數值模擬，得出炸藥起爆初始位置對該物理過程的影響。圖8 為R*d=0.1 時不同時刻氣泡的形態和流場壓力變化圖。

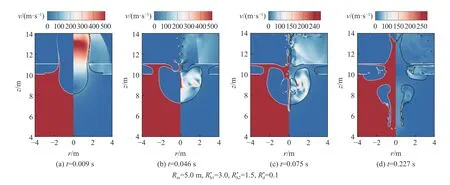
圖8 不同時刻氣泡的形態和流場壓力變化圖Fig. 8 The bubble shape and flow field pressure change at different moments

由圖8 可知，炸藥起爆位置距離結構較近時，自由液面處出現了破碎和重閉合現象。針對R*d=0.1的工況，在初始氣泡膨脹階段，當t=0.009 s 時，氣泡迅速涌入到結構內側，氣泡內氣體運動速度可以達到500 m/s。破口的存在對氣泡的演化具有明顯的誘導作用，在雙層結構的誘導下，當t=0.046 s 時，自由液面出現分流趨勢，上表面在內板的作用下重新閉合。當t=0.075 s 時，由于流體運動較為劇烈，氣泡的羽化破碎和液滴飛濺現象會出現在雙層結構殼內部，這種較為精細的數值模擬用傳統的數值模型是較難實現的。同時，自由表面的相對運動使氣泡產生了向下的“皇冠”型射流。當t=0.227 s 時，在氣泡回彈階段，氣泡進一步破碎形成一些無規則的小氣泡，這也是由于局部流體速度不均勻造成的。相比于4.1 中的工況，涌流形態整體上呈現“飛濺”型，這使得隨著時間推移只有少量流體會涌入到內艙室。

圖9 為不同起爆位置下，艙室涌流量隨時間的變化曲線。由圖9 可知，在初始位置＜0.4 的范圍內，隨著起爆位置與自由液面位置距離的減小，初始瞬間涌流的速度變大（即曲線的斜率較大），水進入艙室所花費的時間越短。而爆炸氣泡脈動誘導的進水量最大值和最終艙室的涌流量卻越小，這是由于初始時刻在氣泡上方的水較少造成的。由此可知，當破口產生后，爆炸產物距離結構越近，其受涌流進水的影響反而越小。由于雙層結構之間間隔的存在，初始階段內艙室的進水量所占的比例較小，水不能完全進入內艙室，進而存在一定的反應時間，這也有利于艦船和潛艇的緊急應急，避免結構沉沒。

圖9 不同起爆位置下艙室涌流量隨時間的變化曲線Fig. 9 Changes of cabin inrush flow with time under different detonation position

4.4 雙層殼間初始水位的影響

艦艇雙層殼之間的水密艙可以用來調節結構自身重力，從而改變其在海里的平衡浮力，由于自由液面的存在，水密艙內水位對本文所涉及的多相流動問題存在較大影響。因此應分析水密艙內水位對近場水下爆炸氣泡與雙層破口結構相互作用的影響。文中選擇=0 ， 0 .5 ，1 .0 分別進行數值模擬，得出雙層殼間初始水位對該物理問題的影響。圖10 為=1.0 時不同時刻氣泡的形態和流場壓力變化圖。

圖10 不同時刻氣泡的形態和流場壓力變化圖Fig. 10 The bubble shape and flow field pressure change at different moments

由圖10 可知，當艙室殼內水位較高時，在靜水壓作用下，整個流場流體特性相對較為穩定。在氣泡膨脹階段，艙室殼內的水就開始涌入內艙室，形成艙室涌流。由于自由液面處水冢速度較大（流速可以達到50 m/s），所以水冢高度不斷升高并帶動周圍空氣產生無規則運動。伴隨著水冢的演化，破口附近液面逐漸收縮，這是由于局部壓力不平衡和涌入雙層殼結構的水與進入艙室內的水的體積差造成的。當t=0.267 s 時，氣泡受浮力作用較明顯，從而產生向下和向上的對射流，其中向上的射流是由于局部較大的靜水液壓導致的。隨著氣泡的演化，當t=0.572 s 時，氣泡穿透進入環狀階段，并進一步破碎形成多個氣泡環。整體上來說，此時破口對氣泡運動影響不明顯，而艙室涌流特性變化較劇烈，接下來將對其進行定量分析。

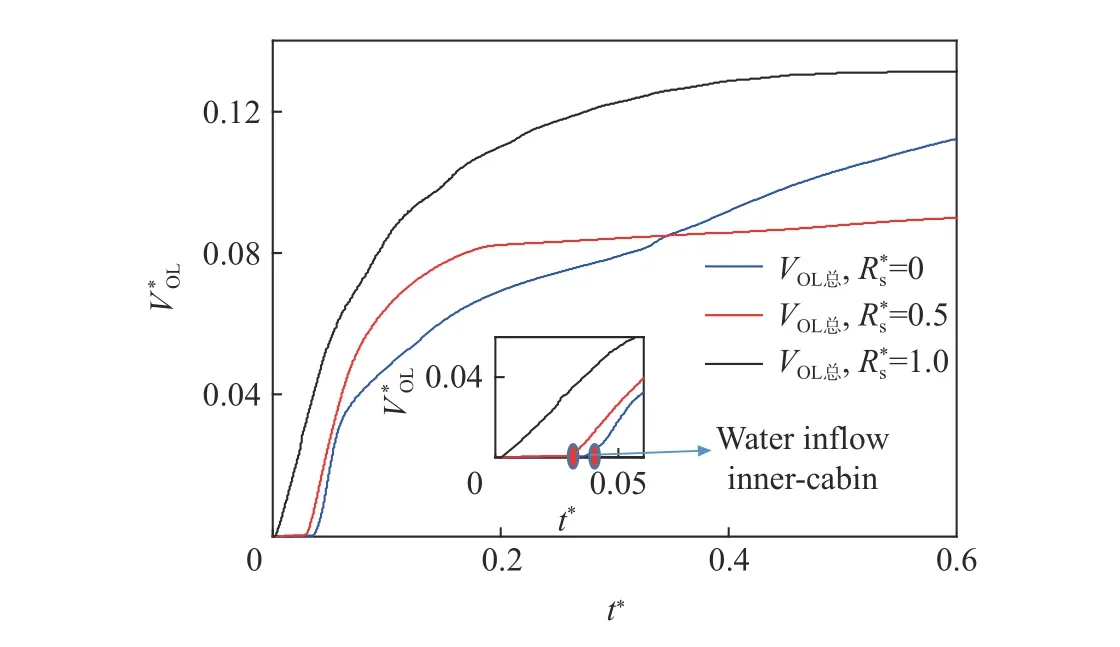
圖11 不同水位下艙室涌流量隨時間的變化曲線Fig. 11 Changes of cabin inrush flow with time at different water levels

5 結 論

基于歐拉有限元方法對近場水下爆炸氣泡與雙層破口結構的相互作用機理進行了研究，對不同破口尺寸，不同起爆位置條件下的不同工況進行了較詳細的對比和分析。具體結論如下：

（1）當R*d=0.4、R*h1=3.0 、R*h2=1.5 時，在內部空氣、流體慣性以及破口誘導的聯合作用下，氣泡演化過程中出現了氣泡分割現象，初始的爆炸氣泡分成了幾個小氣泡和一個較大的主氣泡，多個羽化氣泡繼續演化。

（2）內層破口尺寸越小，內板結構對涌流的抑制作用越大。當R*h2=0.5 時，內艙室內會出現二次涌流現象，且涌流形態較細長。在初始內板破口參數R*h2＜1.5 的范圍內，隨著破口尺寸的增大，內艙室的涌流量增大。因此加強內層板的強度可以有效提高艦艇生命力。

（3）炸藥起爆位置距離結構較近時，自由液面處會出現破碎和重閉合現象。在初始位置R*d＜0.4 的范圍內，隨著起爆位置與自由液面位置距離的減小，初始瞬間涌流的速度變大（即曲線的斜率較大），水進入艙室所花費的時間越短，爆炸氣泡脈動誘導的進水量最大值和最終艙室的涌流量卻越小。

（4）當艙室殼內水位較高時，在靜水壓作用下，整個流場流體特性較穩定。當R*s＜0.5 時，隨著R*s增大，涌流速度逐漸減小，內艙室進水時間逐漸延長，導致艙室的水量增大。當水位滿艙時，急速涌流會縮短船艇的應急時間。所以適當調節艙內水位也可以提高艦艇生命力。