基于干擾觀測器的彈丸協調器電液伺服系統自適應滑模控制

聶守成，錢林方，陳志群，衛俞凱，尹強

(南京理工大學 機械工程學院，江蘇 南京 210094)

0 引言

大口徑火炮彈丸質量較大，高溫高寒等極端環境條件下不便于人工完成彈丸裝填，通常需要借助彈丸協調器將彈丸轉移至輸彈位，由輸彈機完成輸彈。在火炮平臺無人化作戰需求下，彈藥自動裝填系統亦大多采用電液伺服系統來驅動彈丸協調器繞耳軸旋轉、完成彈丸傳遞。彈丸協調器電液伺服系統的快速性有助于提高火炮射速，其較高的到位精度可以獲得更好的輸彈初始條件，進而保證卡膛姿態[1]。因此，提高彈丸協調器電液伺服系統控制性能具有重要的實際應用價值。

反演控制方法[2]廣泛應用于解決電液伺服系統中的非匹配不確定性問題，但使用該方法構建控制器對虛擬控制量進行求導時會出現微分爆炸現象，使控制器設計變得復雜。于是在反演方法基礎上，不同學者結合動態面[3-4]、自適應[5-6]、神經網絡[7]等方法構建復合反演控制器，均獲得了一定的性能改善。針對電液伺服系統中的不確定性和非線性，Yao等[8-9]提出一種結合自適應控制和滑模控制的自適應魯棒控制(ARC)方法，獲得理想的漸進穩定性和預期的瞬態性能，并將該方法應用于雙出桿電液伺服系統中，基于不連續映射算法構建了自適應魯棒控制器，結果表明該算法具有較好的瞬態特性和跟蹤性能。

當電液伺服系統中存在非匹配外部擾動時，一些學者通過構建擾動觀測器[10-12]來觀測擾動，在設計控制器時引入擾動觀測器觀測值對擾動進行補償控制，以有效提高控制精度和魯棒性。Chen等[13]設計了一種在有限時間內收斂的擾動觀測器。劉龍等[14]采用擾動觀測器分別對匹配和非匹配模型的不確定項進行觀測，結合滑模面構造新型控制器，有效削弱了滑模控制的抖振并獲得了良好的跟蹤性能。

本文結合彈丸協調器電液伺服系統的特點建立系統狀態方程，針對狀態方程中的非匹配不確定項，設計干擾觀測器觀測彈丸協調器電液伺服系統中的非匹配不確定性；采用自適應算法估計系統的參數不確定性，進而提出一種新型積分滑模面，結合干擾觀測器和自適應算法構建積分滑模控制器，對系統中的非匹配不確性和參數不確定性進行補償控制，并通過實驗驗證算法的有效性。

1 系統建模與問題描述

彈丸協調器電液伺服系統結構示意圖如圖1所示，主要由協調臂、協調油缸、比例伺服閥、液壓油源和控制器組成，其中彈丸協調臂在協調油缸驅動下繞耳軸O轉動。圖1中，α為彈丸協調器角位移，h(α)為耳軸O點到協調油缸的距離，pn和py分別為協調油缸無桿腔壓力和有桿腔壓力，M和N分別為協調油缸下耳軸支點和上耳軸支點，β為協調臂初始位置時OM與ON的夾角，Qi和Qo分別為系統進油和回油流量，rOM、rON分別為點O到點M和點N的距離，m為協調器總質量，rg為點O到協調器質心的距離，u為比例伺服閥控制輸入電壓，ps為系統供油壓力，pr為系統回油壓力，0 MPa≤pr≤pn≤ps，0 MPa≤pr≤py≤ps.

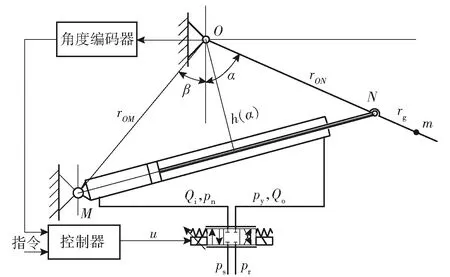
圖1 彈丸協調器位置關系示意圖Fig.1 Schematic diagram of ammunition manipulator location

彈丸協調器電液伺服系統的力矩平衡方程為

(1)

(2)

對協調油缸無桿腔和有桿腔分別應用流量連續性方程,可得

(3)

式中：Cip為協調油缸內泄漏系數；Cep為協調油缸外泄漏系數；βe為油液體積彈性模量；V0n和V0y分別為任意時刻協調油缸無桿腔和有桿腔及其相連管路內的油液體積。

Qi、Qo和比例伺服閥控制輸入電壓u的關系可表示為

Qi=kqvuRn，
Qo=kqvuRy，

(4)

式中：kqv為比例伺服閥流量增益系數；Rn和Ry由(5)式確定：

(5)

函數s(*)由(6)式確定：

(6)

(7)

(8)

系統在實際工作過程中，B、Tg、βe、Cip、Cep等參數由于受到各類環境因素的影響會隨時間變化，本文中將B和Tg的參數不確定性等效為d2(t)，將βe、Cip、Cep、V0n和V0y等參數不確定性對系統的影響等效為擾動項θ(t)，從而可將(8)式改寫為

(9)

式中：d(t)=d1(t)+d2(t)。

給定理想的角度軌跡指令xd，彈丸協調器應能夠跟蹤其軌跡，因此本文設計的滑模控制器控制輸出u必須保證連續有界。為了便于描述滑模控制器設計過程，需要進行如下假設：

假設1非匹配不確定性項d(t)d有界，且其1階導數存在，d≤D，D為有界正實數。

假設2參數不確定性項θ(t)θ有界，且θ≤Θ，Θ為有界正實數。

(10)

式中：θmax、θmin分別為θ的最大值和最小值。

為了得到θ的估計值并保證其有界，定義如下自適應率：

(11)

式中:γ>0；τ為待確定自適應率。

2 控制器設計

2.1 干擾觀測器設計

針對彈丸協調器電液伺服系統狀態方程(8)式中的非匹配不確定性項，設計有限時間收斂干擾觀測器，定義干擾觀測器變量[13]s1為

s1=z1-x2，

(12)

式中：z1由(13)式給出，

(13)

p0和q0為正奇數，p0D，f(x1,x2)=-Bh2(x1)x2-Tgsinx1.

定義d的估計值為

(14)

對變量s1求導，得

(15)

由(8)式、(13)式和(14)式，可得d的估計誤差為

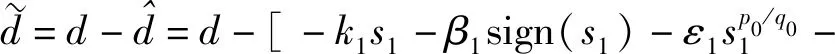
(16)

定義Lyapunov函數

(17)

對V1求導，有

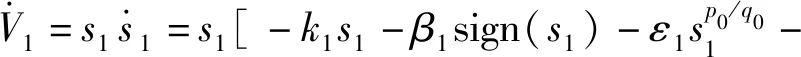
(18)

2.2 滑模自適應控制器設計

傳統的滑模變結構控制一般選取切換函數為

s0=c1e1+c2e2+…+ciej+…+
cn-1en-1+en，

(19)

在切換函數中引入跟蹤誤差的積分項，并采用狀態變量代替誤差項，可以消除跟蹤信號的各階導數項，切換函數[15]可以改寫為

(20)

式中：c0為滑模參數，c0>0；te為結束時間。

為了有效抑制(8)式中的非匹配不確定性，在切換函數中引入干擾觀測器，因此將切換函數[16]定義為

(21)

對s求導，得

(22)

設計控制器u為

(23)

式中：k為控制器切換增益，k>0.

(23)式代入(22)式，得

(24)

定義Lyapunov函數

(25)

對V求導，有

(26)

取自適應律

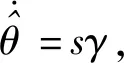
(27)

(27)式代入(26)式，得到

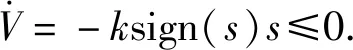
(28)

由(28)式易知,由(8)式、(14)式、(23)式以及(27)式構成如圖2所示的閉環控制系統是穩定的。

圖2 控制系統結構Fig.2 Structure diagram of control system

為了進一步削減抖振，采用飽和函數sat()代替符號函數sign():

(29)

式中：Δ為邊界層厚度，Δ>0.

3 實驗驗證與分析

為了驗證本文提出的控制策略，搭建如圖3所示的實驗平臺。上位機通過CANOpen網絡與可編程邏輯控制器(PLC)進行信息交互，PLC通過模擬量輸入(AI)模塊和壓力傳感器相連，獲取協調油缸兩腔壓力信號，彈丸協調臂位置信息由編碼器通過CANOpen網絡上傳至PLC控制器，控制電壓由PLC通過模擬量輸出(AO)模塊送達比例伺服閥，彈丸協調臂在協調油缸驅動下到達指定位置。

圖3 彈丸協調器電液伺服系統Fig.3 Electro-hydraulic servo system of ammunition manipulator

彈丸協調器電液伺服系統的主要物理參數如表1所示。

表1 系統參數表Tab.1 Parameters of the system

根據彈丸協調器完成規定動作的時序要求，彈丸協調器從α=0°分別運動至45°、60°和90°時的期望位置xd曲線分別如圖4所示。

圖4 期望位置曲線Fig.4 Desired position curves

本文設計的控制器參數取值為：k1=2 350，β1=5，ε1=0.05，p0=5，q0=9，c0=1 250，c1=155，c2=45，k=10，γ=0.015，Δ=2.為了驗證本文提出算法的有效性和穩定性，首先在彈丸協調器不帶彈的情況下進行45°協調動作實驗。圖5和圖6所示分別為彈丸協調器軌跡跟蹤誤差e1和比例伺服閥控制輸入u.

圖5 不帶彈軌跡跟蹤誤差Fig.5 Tracking error without projectile

從圖5和圖6中可以看出：彈丸協調器向上協調動作過程中最大動態跟蹤誤差為-1.19°，最大控制量為3.51 V；向下協調動作過程中最大動態跟蹤誤差為1.18°，最大控制量為-4.06 V；向上向下協調過程中穩態誤差均小于0.02°，動態誤差和穩態誤差均滿足性能要求，表明本文設計的控制器具有較好的跟蹤性能。

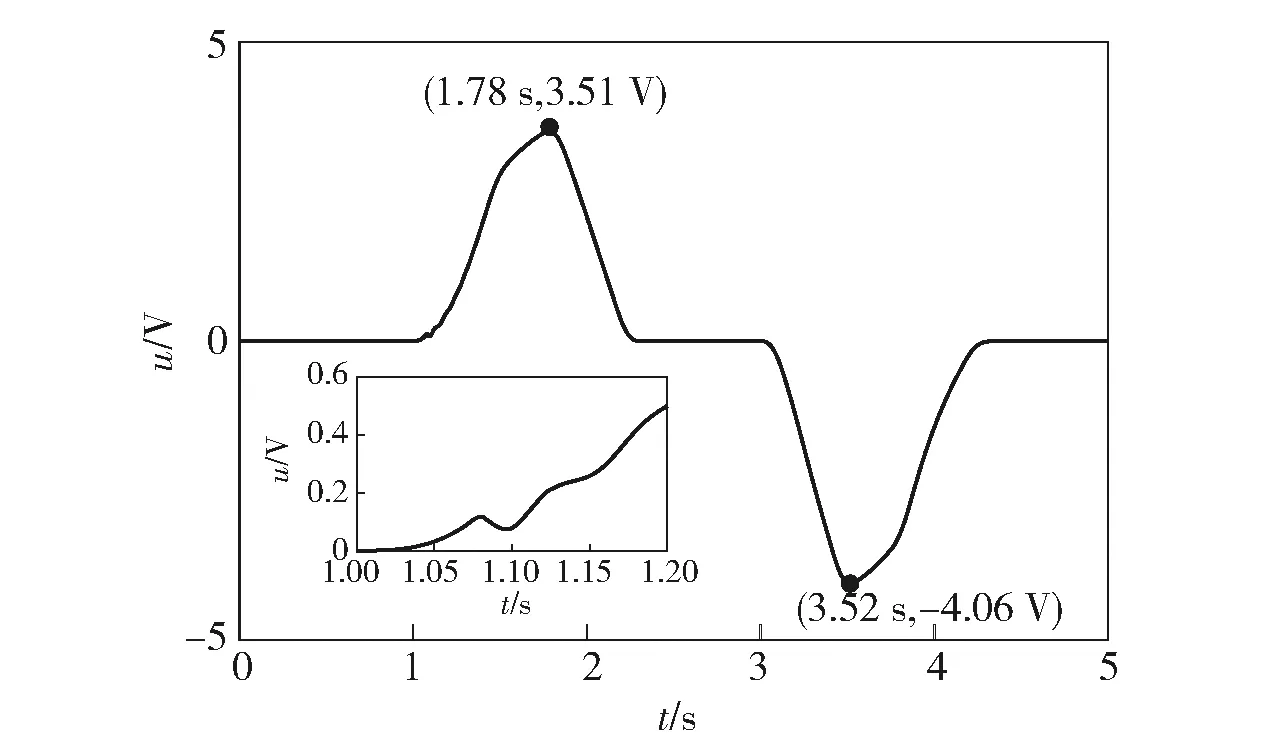
圖6 不帶彈控制輸入Fig.6 Control input without projectile

從圖6中還可以看出，在彈丸協調器向上協調運動的初始階段，控制量發生輕微的抖動。這是因為初始時刻彈丸協調器的系統重心位于鉛垂面的一側，而彈丸協調器的平衡位置為系統重心與鉛垂面重合的位置。當彈丸協調器運動經過該位置時，重力分量對協調器運動的作用方向發生變化，控制量出現抖動，而在其余過程中，控制量均較為平滑。此外，圖6中彈丸協調器向下運動時的控制量明顯大于向上運動時的控制量，這是因為在無桿腔回路中加入了抗衡閥，其作用是為了避免彈丸協調器向下運動時因重力作用發生誤動作。彈丸協調器實際工作過程中，輸彈指令發出時，彈丸協調器從接彈位將彈丸轉運至輸彈位，由輸彈機完成輸彈，然后彈丸協調器返回接彈初始位置。根據圖4中提供的期望位置曲線，分別在45°、60°和90°進行彈丸協調器協調動作實驗，實驗結果如圖7～圖10所示。

圖7和圖8所示分別為彈丸協調器在各個角度下運動的軌跡跟蹤誤差和控制輸入。圖7和圖8中曲線表明，在不同期望角度下，協調器軌跡跟蹤誤差和控制量變化均較為平穩，在不同負載下變化規律基本一致，未發生異常波動。隨著期望角度的增加，動態軌跡跟蹤誤差有所增大，3種工況分別為1.33°、1.69°和2.15°，均在系統精度可接受的范圍內，3種工況的穩態誤差均保持在0.03°以內，到位精度符合控制要求。

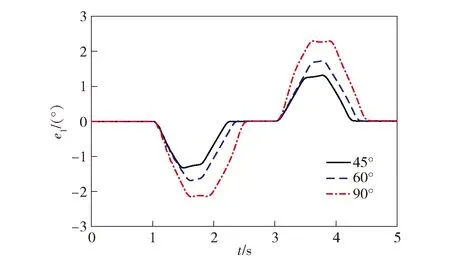
圖7 帶彈軌跡跟蹤誤差Fig.7 Tracking errors with projectile

圖8 帶彈控制輸入Fig.8 Control inputs with projectile

從圖7中可以明顯看出，由于液壓回路中抗衡閥的存在，彈丸協調器向下運動時的控制量明顯高于向上運動時的控制量，而整個過程中軌跡跟蹤誤差均符合要求且無明顯波動，表明控制器能夠適應系統的結構特性，且具有較好的魯棒性。

圖9和圖10分別為干擾觀測器估計值和自適應律的估計值。從中分析可知：(8)式中的非匹配不確定性d(t)主要來自未知的系統摩擦和負載特性變化，隨著彈協調器協調角度增大，系統摩擦力將會增大，且該過程中彈丸協調器重力分量產生的反作用力矩也隨之增加，與圖9中曲線變化趨勢一致；(8)式中的參數不確定性項θ(t)主要來自油液壓縮性和液壓泄漏，彈丸協調器運動角度越大、速度越快，則該不確定性變化愈劇烈，與圖10中自適應估計值曲線較為符合。綜上所述，圖9和圖10中干擾觀測器估計和自適應估計的變化趨勢均與彈丸協調器動作規律符合，且在協調器到位時有明顯收斂趨勢，表明干擾觀測器和自適應律能夠較為理想地刻畫系統實際特性，從而為彈丸協調器控制提供參考。

圖9 干擾觀測器輸出Fig.9 Outputs of disturbance observer

圖10 自適應估計Fig.10 Estimation of the adaptive law

4 結論

本文針對彈丸協調器電液伺服系統中存在的非匹配不確定性和參數不確定性問題，提出一種基于干擾觀測器的自適應滑模控制策略。所設計的干擾觀測器用于估計模型中的非匹配不確定性，采用自適應算法估計系統中的參數不確定性，并將干擾觀測器引入切換函數設計中，結合自適應算法實現彈丸協調器電液伺服系統的位置跟蹤控制。

實驗結果表明，本文設計的控制器能夠較好地完成彈丸協調器的跟蹤控制要求，所設計的干擾觀測器和自適應律能夠準確刻畫系統特性，系統動態跟蹤誤差和穩態精度均滿足控制要求，魯棒性較強，可以為協調器快速高精度控制提供依據。