基于時變O-U均值回復模型的天氣衍生品定價研究

唐欣 鄒楚瑜

[摘要]馬鈴薯作為我國主要的糧食作物，其產量受天氣狀況的影響較大。河北省張北、圍場和豐寧三地是馬鈴薯種植最集中的區域，異常的天氣波動會給當地農戶帶來嚴重的經濟損失。天氣衍生品可以幫助農戶對沖農作物面臨的天氣風險，但要達到良好的風險對沖效果，就需要更加精準的定價模型。本文致力于尋求精度更高的定價模型，于是在傳統的Ornstein-Uhlenbeck均值回復模型的基礎上，引入時間序列模型來重新模擬均值回復速度，得到時變均值回復模型。之后，使用張北、圍場、豐寧三地1951—2018年的日平均氣溫數據擬合2019年每日平均氣溫的動態變動過程，并檢驗模型預測精準度。最后，在此基礎上，借助蒙特卡羅模擬法測算馬鈴薯生長溫度指數期貨合約的價格，并與傳統的均值回復模型的定價結果做比較。研究表明，時變Ornstein-Uhlenbeck均值回復模型能夠較好地擬合氣溫的變動趨勢，并且比傳統的Ornstein-Uhlenbeck均值回復模型更能精準地預測期貨價格。

[關鍵詞]天氣衍生品;時變O-U均值回復模型;均值回復速度;生長溫度指數

中圖分類號：F842.66 文獻標識碼：A DOI：10.16465/j.gste.cn431252ts.202008

中國是馬鈴薯生產第一大國，而河北省的張北、圍場和豐寧又是我國重要的種薯繁育、商品薯生產加工以及儲運基地，具有十分重要的戰略地位。馬鈴薯產業的發展對河北省農民精準脫貧、增收及糧食安全生產具有重要意義。而天氣狀況日益多變，可能會導致馬鈴薯減產，最終會波及整條馬鈴薯產業鏈，影響農戶福祉。我國現有的政府補貼和農產品保險無法完全彌補天氣風險管理的缺口，因此需要開發新型的天氣風險管理工具，天氣衍生品就是其中之一。天氣衍生品誕生于1996年，是以天氣指數作為標的資產的金融衍生工具，用以對沖天氣反常變化帶來的收入不確定性，這類產品在國外被廣泛運用于天氣敏感性行業的風險管理策略，其中就包括農業領域。但在我國，天氣衍生品領域還是一片空白。

1 文獻綜述

在天氣衍生品領域的研究中，普遍采用時間序列模型、Ornstein-Uhlenbeck均值回復模型（以下簡稱O-U均值回復模型）以及神經網絡模型作為氣溫預測模型。研究思路大致分為三種，一是基于時間序列模型，如利用ARIMA模型、AR-GARCH模型對每日平均氣溫時間序列進行分析和預測;二是基于O-U均值回復模型，假設氣溫變量服從隨機布朗運動，并利用蒙特卡羅仿真模擬來對天氣衍生品進行定價;三是利用小波分析對氣溫序列進行分解和重構，并結合神經網絡技術進行預測，以此來為天氣衍生品定價。

國外學界對O-U均值回復模型的研究由來已久。Vasicek O[1]于1977年率先提出了利率變動的O-U均值回復模型，他認為利率的變化雖然是隨機的，但是長期利率傾向于回歸長期均值水平。O-U均值回復模型被運用于氣溫預測始于1998年，Dischel B[2]提出基于隨機微分方程（SDE）的氣溫預測模型，并首次建立了平均氣溫的均值回復模型。而后，眾多學者對Dischel提出的均值回復模型進行了實證檢驗和改進。Dornier F等[3]使用這一模型進行平均氣溫的預測，值得一提的是，他們將氣溫的波動率考慮為一個常數。Alaton P等[4]于2002年用一個正弦函數來描述溫度的季節性變動，將溫度的波動率考慮為按月變化的常數，提出了基于月波動率的O-U均值回復模型，并以此模型結合蒙特卡羅模擬對氣溫期權進行定價分析，得到了較好的實證效果。2003年Bhowan A[5]通過進一步的研究發現，氣溫的波動率并非按月變化的常數，其變化規律同樣呈現出均值回復的特性。Benth F E等[6]在此基礎上將溫度的波動率考慮為日波動率，并對氣溫的季節項進行傅里葉變換，用多個正弦和余弦函數來描述氣溫的季節性變化，進而提出了基于日波動率的O-U均值回復模型，該模型成為運用最為普遍的氣溫預測模型。

而國內學界關于O-U均值回復模型對天氣衍生品定價方面的研究不夠深入，但起步其實并不晚。2006年劉國光[7]通過Alaton提出的基于月波動率的O-U均值回復模型，結合1980—1999年的北京每日平均氣溫數據進行模型參數估計，并運用蒙特卡羅仿真模擬法為天氣期權和天氣互換定價，實驗效果較好。然而一直到2011年，國內學者才開始在劉國光的基礎上進行改進。李永等[8]在2011年以O-U均值回復模型為基礎，通過回歸分析和傅里葉變換求得相關參數，并對上海地區1951—2008年的氣溫進行研究，發現預測值的相對誤差絕對值均小于5%。2012年李永等[9]又以上海氣溫為例利用帶Levy過程的O-U均值回復模型對天氣衍生品定價的合理性進行測度，較好地模擬了氣溫的變化。此外，部分國內學者對傳統的O-U均值回復模型還貢獻了全新的研究思路，他們將均值回復速度設置為以年為單位的分段函數，由于每年的均值回復速度存在一定的差異，故將模型命名為時變O-U均值回復模型。其中最具代表性的研究是陳百碩等[10]在2014年和王明亮等[11]于2015年發布的兩篇文獻，均證明這種時變模型可以更好地擬合氣溫變動過程。本文也將延用這種方法進行實證分析。

2 時變均值回復模型和氣溫指數模型的建立

2.1 時變均值回復模型

2.1.1 模型的建立

3 實證與結果分析

3.1 基于時變O-U均值回復模型的氣溫預測

3.1.1 數據說明

本文選取了河北省三個主要的馬鈴薯產地張北、圍場、豐寧1960年1月1日至2019年12月31日的日平均氣溫數據作為實驗樣本（單位℃，精確到0.1℃，共60年，去除閏年2月29日以后共計65 700個數據）。

3.1.2 氣溫時間序列的參數估計

由公式（5），對三個城市的日平均氣溫序列進行線性和非線性回歸分析，在各參數均通過顯著性檢驗的前提下，得到各自的氣溫長期趨勢St：

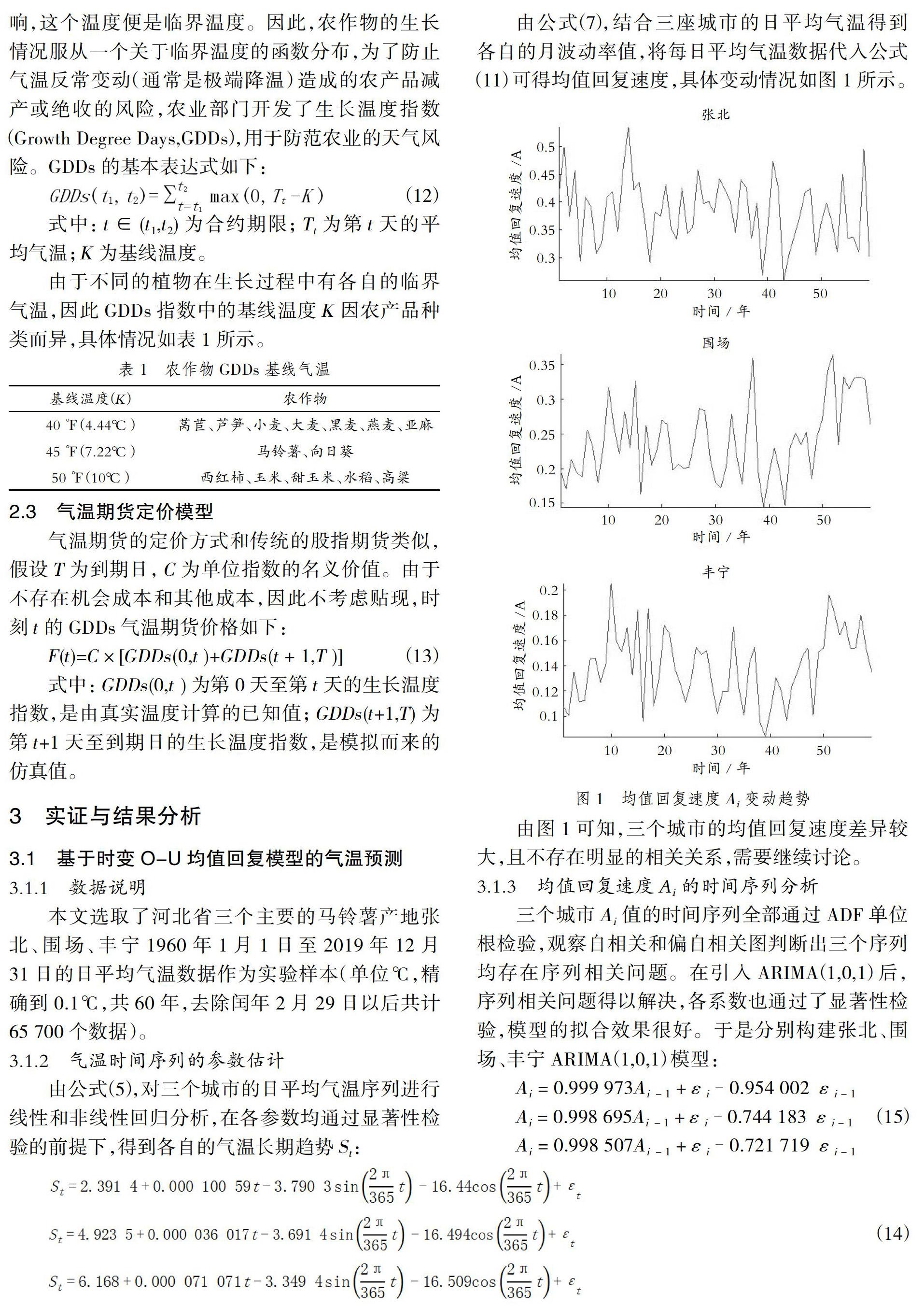
由公式（7），結合三座城市的日平均氣溫得到各自的月波動率值，將每日平均氣溫數據代入公式（11）可得均值回復速度，具體變動情況如圖1所示。

由圖1可知，三個城市的均值回復速度差異較大，且不存在明顯的相關關系，需要繼續討論。

3.1.3 均值回復速度Ai的時間序列分析

三個城市Ai值的時間序列全部通過ADF單位根檢驗，觀察自相關和偏自相關圖判斷出三個序列均存在序列相關問題。在引入ARIMA（1，0，1）后，序列相關問題得以解決，各系數也通過了顯著性檢驗，模型的擬合效果很好。于是分別構建張北、圍場、豐寧ARIMA（1，0，1）模型：

3.2 天氣衍生品的設計與定價

3.2.1 標的指數的計算

本文選擇基于馬鈴薯的GDDs指數期貨定價。由于馬鈴薯的種植期多集中于第四季度，因此選取7.22℃作為馬鈴薯GDDs指數的基線溫度，對預測得到的氣溫數據進行轉化，得到三個城市2019年10月—12月（第四季度）分別的生長溫度指數GDDs，通過與2019年實際的GDDs指數做對比，來判斷時變O-U均值回復模型的預測精度，結果如表2所示。

由此可見，三座城市的GDDs指數的預測值和真實值之間的偏差率均不超過8%，說明兩種預測精度較好，并且時變O-U均值回復模型的預測精度要比傳統的O-U均值回復模型更高，能夠更好地擬合氣溫變動情況。

3.2.2 天氣衍生品的設計與定價

本文為張北、圍場和豐寧分別設計一份天氣衍生品期貨合約。按照芝加哥商品交易所（CME）對天氣指數期貨合約的規定，合約規格設置如表3所示。

結合公式（13）將GDDs指數轉化為合約價格。假設買方分別在10月1日、11月1日、12月1日進入期貨多頭或空頭，分別計算三個時點的期貨價格，比較兩種模型預測的合約價格與真實價格的偏差程度，判斷時變O-U均值回復模型的改進效果。由于篇幅原因只以豐寧為例進行展示，如表4所示。

由表4可知，當以豐寧為標的城市時，兩種O-U均值回復模型都能較好地貼近期貨的價格，預測的偏差率均小于5%，且時變模型效果更佳。其他兩座城市以兩種模型進行實證分析的效果均較好，大部分預測偏差率小于8%（個別值除外），并且時變模型整體效果要優于傳統模型，雖然精度提升的幅度不大（平均提高0.2%左右），但是由于交易體量較為龐大，依舊能明顯改善期貨的作用效果。此外，兩種模型模擬不同城市的期貨價格的效果不同，其中對豐寧的期貨價格的預測效果最佳（平均誤差率不超過3%）。

4 結論與展望

本文著眼于提高傳統的天氣衍生品定價模型——O-U均值回復模型的預測精準度，將均值回復速度從常數改進為ARIMA時間序列，構建時變O-U均值回復模型。以河北省張北、圍場和豐寧三個馬鈴薯種植大縣為例，選取1960—2019年的日平均氣溫數據，對時變O-U均值回復模型的預測精確度進行了實證分析。之后，基于馬鈴薯的生長溫度指數GDDs設計天氣期貨產品，利用蒙特卡羅模擬法擬合了期貨合約的價格，并與傳統的O-U均值回復模型的擬合結果做比較分析，考察兩個模型的效果差異。研究發現，三個城市的均值回復速度變動趨勢各不相同，但均適合引入ARIMA（1，0，1）模型，并且改進后的時變O-U均值回復模型對氣溫變化過程的擬合程度較好。此外，時變O-U均值回復模型在期貨定價方面展現出了比傳統O-U均值回復模型更好的預測精度。

在得到上述研究結論的同時，本文還提出一些展望。第一，雖然本文選取的三個城市的均值回復速度均適合ARIMA（1，0，1）模型，但這并不代表其他地區也同樣適合這一模型，具體的論證需要后續研究跟進。第二，雖然本文以三個城市為例證明了時變O-U均值回復模型的擬合效果更佳，但三個城市均來自同一地區，這種空間局限性表明時變O-U均值回復模型在我國其他地區未必擁有同樣的作用效果，具體情況需要通過進一步拓展研究進行論證。第三，以天氣期貨為代表的諸多天氣衍生品具有良好的天氣風險規避效果，并已經得到了國外資本市場20余年的檢驗，但是這一金融創新產品還未在我國成為正規的場內交易產品，希望有關部門可以盡快推動天氣衍生品在我國證券市場的發行與流通，讓這一產品真正幫助農戶、企業以及整個農業對沖面臨的天氣風險。

參考文獻

[1] Vasicek O.An Equilibrium Characterization of the Term Structure[J].Journal of Financial Economics，1977，5 （2）：177-188.

[2] Dischel B.At last： A Model for Weather Risk[J].Energy and Power Risk Management，1998（1）：78-86.

[3] Dornier F，Queruel M.Caution to wind.Energy Power Risk Management[J].Weather Risk Special Report，2000（1）：30-32.

[4] Alaton P，Djehiche B，Stillberger D.On Modelling and Pricing Weather Derivatives[J].Applied Mathematical Finance，2002，9（1）：1-20.

[5] Bhowan A.Temperature Derivatives[R].School of Computational and Applied Mathematics，University of ? Wiwatersrand，2003.

[6] Benth F E，Saltyte B J.The Volatility of Temperature and Pricing of Weather Derivatives[J].Quantitative Finance，2007，7（5）：553-561.

[7]劉國光.天氣預測與天氣衍生產品定價研究[J].預測，2006，25 （6）：28-33.

[8]李永，夏敏，吳丹.O-U模型在天氣衍生品定價中的合理性測度[J].統計與決策，2011（21）：32-35.

[9]李永，夏敏，梁力銘.基于O-U模型的天氣衍生品定價研究：以氣溫期權為例[J].預測，2012，31（2）：18-22+37.

[10]陳百碩，李守偉，何建敏，等.天氣衍生品中時變均值回復的氣溫預測模型研究[J].管理工程學報，2014，28（2）：145-150.

[11]王明亮，何建敏，陳百碩，等.時變O-U模型在氣溫預測及氣溫期貨定價中的適應性研究：基于北京市1951—2012年的日平均氣溫數據[J].中國管理科學，2015，23（2）：44-49.