水文循環(huán)算法的改進(jìn)

何欣蕓，周朝榮,2+

(1.四川師范大學(xué) 物理與電子工程學(xué)院，四川 成都 610101；2.成都信息工程大學(xué) 氣象信息與信號處理四川省高校重點實驗室，四川 成都 610225)

0 引 言

近年來，受自然界中水運動的啟發(fā)，一些基于水的智能優(yōu)化算法迅速發(fā)展起來。Hosseini基于河流中水滴間的作用與反作用，提出智能水滴算法[1]。Yang等模擬水流運動設(shè)計出類水流算法[2]。Rabanal等借鑒河流形成動力學(xué)來解決NP-Hard問題[3]。通過觀察水的循環(huán)過程以及河流、溪流的運動，Eskandar等設(shè)計出水循環(huán)算法，并應(yīng)用于約束優(yōu)化問題的求解[4]。Wu等受淺水波模型啟發(fā)，提出水波算法[5]。這些受水運動啟發(fā)的算法由于參數(shù)少、易調(diào)節(jié)、模型簡單等優(yōu)點受到了許多學(xué)者的關(guān)注。

然而，上述算法只涉及到自然界中水運動的部分過程，未考慮到完整的水循環(huán)運動，只模擬水運動的部分過程會限制算法搜索能力，造成算法早熟收斂。為此，Wedyan等模擬水的循環(huán)再生過程提出水文循環(huán)算法(hydrological cycle algorithm，HCA)，并通過仿真實驗驗證水文循環(huán)算法在連續(xù)問題與離散問題上均優(yōu)于僅模擬部分水運動的算法[6,7]。其中，水文循環(huán)是指水在自然界中的連續(xù)循環(huán)運動，包括水受重力與地勢影響從高處向低處流動、受陽光照射蒸發(fā)到大氣層以及在空中凝結(jié)成水滴重新落回地面等階段。HCA利用完整的水循環(huán)過程，為算法設(shè)計提供新的思路。

然而，HCA仍存在收斂速度慢、尋優(yōu)精度不高以及運行時間較長等問題。為此，本文首先在HCA的種群初始化階段采用混沌的方法，強化全局搜索能力、加快收斂速度；其次，自適應(yīng)產(chǎn)生溫度更新參數(shù)，以減少算法的運行時間；最后，在凝結(jié)階段引入逆水流過程，以提高算法的尋優(yōu)精度。為驗證改進(jìn)后的算法性能，在10個經(jīng)典函數(shù)上進(jìn)行仿真測試，并與粒子群算法[8]、遺傳算法[9]與鯨魚算法[10]進(jìn)行比較。測試結(jié)果表明，改進(jìn)后的算法在尋優(yōu)精度、收斂速度以及運行時間上較HCA表現(xiàn)更優(yōu)，且總體性能優(yōu)于粒子群算法、遺傳算法與鯨魚算法。

1 水文循環(huán)算法

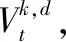
1.1 流動階段

水滴在具有數(shù)條等高線的山形圖上進(jìn)行流動，山形圖個數(shù)由函數(shù)的維度決定，等高線條數(shù)由算法精度決定，越靠近山頂?shù)牡雀呔€所占權(quán)重越大。

水滴從山頂出發(fā)，在每層等高線上選擇移動到某個節(jié)點。水滴遍歷完所有等高線后，各個維度中存儲著水滴在該維山形圖的等高線上所選節(jié)點。

流動階段涉及到節(jié)點選擇與次數(shù)、速度、土壤量、溫度的更新，實現(xiàn)原理如下：

(1)節(jié)點選擇

水滴在山形圖上移動時，根據(jù)下一層等高線上節(jié)點的選擇概率，采用輪盤賭的方法選出節(jié)點。水滴在節(jié)點i的位置選擇下一層等高線上節(jié)點j的概率給出如下

(1)

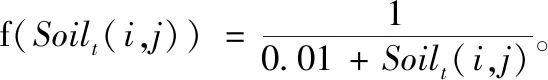
移動到新的節(jié)點后，立即更新該段路徑被選次數(shù)、土壤量以及水滴的速度和所攜帶的土壤量。

(2)溫度更新

一次流動階段結(jié)束時，基于此時水滴的適值差異更新溫度

Temp(T+1)=Temp(T)+ΔTemp

(2)

1.2 蒸發(fā)階段

在蒸發(fā)階段，被蒸發(fā)的水滴的個數(shù)隨機生成，用輪盤賭的方法選擇出被蒸發(fā)的水滴。

1.3 凝結(jié)階段

蒸發(fā)后的水滴按如下方式進(jìn)行變異

(3)

1.4 降雨階段

在降雨階段，若達(dá)到最大迭代次數(shù)則輸出最優(yōu)解；否則，重新初始化動態(tài)變量與參數(shù)，利用本次迭代得到的最優(yōu)解對動態(tài)參數(shù)進(jìn)行加固處理，以指導(dǎo)下一代尋優(yōu)。參數(shù)加固計算如下

Soil(i,j)=0.9×Soil(i,j) ?(i,j)∈BestWD

(4)

其中，BestWD表示本次迭代得到的最優(yōu)解，?(i,j)∈BestWD表示該最優(yōu)解在流動階段所選路徑。

2 改進(jìn)的水文循環(huán)算法

HCA的初始水滴種群隨機產(chǎn)生，多樣性難以保證，會對算法的性能造成顯著影響，初始種群分布越均勻的算法具有更高的收斂速度與尋優(yōu)精度[11]。為此，考慮混沌方法豐富初始種群的多樣性。其次，HCA將溫度更新參數(shù)設(shè)置為固定值，個別優(yōu)化函數(shù)在流動階段內(nèi)循環(huán)多次，以致算法運行時間過長。因此，針對不同的優(yōu)化函數(shù)設(shè)置不同的溫度更新參數(shù)。最后，為解決尋優(yōu)精度低的問題，基于原算法中的山形圖，提出水滴逆向運動模型，即“逆水流”過程。該過程舍棄原算法流動階段中的復(fù)雜參數(shù)與公式，不僅模型更為簡單，且有效地提高了算法的尋優(yōu)精度。

2.1 混沌初始化

混沌是具有遍歷性、半隨機性以及初始條件依賴性的一種非線性系統(tǒng)[12]。與隨機初始化相比，利用混沌進(jìn)行初始化可以產(chǎn)生分布更均勻的初始種群[13]。Skew Tent混沌映射模型簡單、具有較好的遍歷性，且初始條件的依賴性低。本文采用Skew Tent混沌映射對水滴種群進(jìn)行初始化[14]

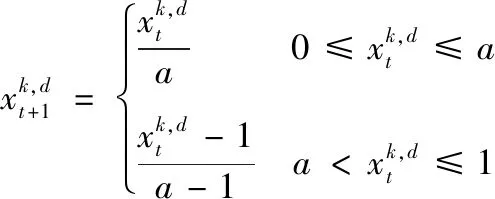
(5)

(6)

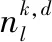
2.2 自適應(yīng)溫度更新參數(shù)

HCA在優(yōu)化某些問題時，一次流動階段結(jié)束后的水滴適值相差較大，溫度增長緩慢，算法在流動階段多次循環(huán)，最終導(dǎo)致整個算法的運行時間過長。為此，采用自適應(yīng)溫度更新參數(shù)代替原算法中固定的溫度更新參數(shù)，由初始種群的適值來決定溫度的增長速度，從而降低算法的運行時間。

在種群初始化階段結(jié)束后，評估水滴種群的適值，根據(jù)最差適值ψmax與最優(yōu)適值ψmin計算溫度更新參數(shù)

(7)

2.3 逆水流

針對HCA容易陷入局部最優(yōu)的問題，利用已有的山形圖，設(shè)計逆水流代替原凝結(jié)階段的變異操作，以提高算法的尋優(yōu)精度。

水滴開始逆流時，首先從山腳出發(fā)，向高層等高線移動。在此過程中，同層等高線上的節(jié)點間彼此連通，水滴在同層等高線上移動后，再移向更高層的等高線。對應(yīng)的逆水流過程如圖1所示。

圖1 逆水流過程

水滴在某一層等高線上移動時，隨機選擇一個節(jié)點數(shù)值比原節(jié)點數(shù)值小的節(jié)點，然后評估該節(jié)點。若對應(yīng)的水滴適值優(yōu)于原節(jié)點，則替換掉原節(jié)點，并繼續(xù)隨機選擇一個數(shù)值更小的節(jié)點，直至選擇數(shù)值更小的次數(shù)達(dá)到上限。

若所選節(jié)點對應(yīng)的水滴適值更差，或原節(jié)點的數(shù)值已是最小，或選擇數(shù)值更小的次數(shù)已達(dá)上限，則在該層隨機選擇一個節(jié)點數(shù)值比原節(jié)點數(shù)值更大的節(jié)點。進(jìn)一步地，評估該節(jié)點，若適值更優(yōu)則進(jìn)行替換，并繼續(xù)選擇數(shù)值更大的節(jié)點直至次數(shù)達(dá)到上限；若適值更差，或是原節(jié)點的數(shù)值已是最大，則水滴流入上一層等高線。

水滴逆流的完整過程見表1。

表1 逆流過程

當(dāng)流動階段結(jié)束后，每顆水滴生成的解以節(jié)點數(shù)組的形式存儲在水滴中。在逆流過程中，水滴首先改變底層等高線上的節(jié)點，由于底層等高線所占權(quán)重小，此時可視為局部搜索；當(dāng)水滴逆移動到較高層等高線時，可視為全局搜索。

2.4 改進(jìn)算法的流程圖

HCA結(jié)合上述混沌初始化與自適應(yīng)溫度更新參數(shù)策略，得到溫度自適應(yīng)水文循環(huán)算法(THCA)；HCA結(jié)合上述混沌初始化與逆水流策略，得到逆水文循環(huán)算法(IHCA)；HCA同時結(jié)合上述混沌初始化、自適應(yīng)溫度更新參數(shù)以及逆水流策略，得到溫度自適應(yīng)逆水文循環(huán)算法(TIHCA)。其中，TIHCA的流程如圖2所示。

圖2 溫度自適應(yīng)逆水文循環(huán)算法流程

3 實驗結(jié)果及分析

3.1 實驗環(huán)境

仿真實驗的運行環(huán)境為Intel Core i7 CPU，主頻2.40 GHz，內(nèi)存8 GB，Windows10 64位操作系統(tǒng)，實驗仿真軟件采用MATLAB R2016a。

3.2 測試函數(shù)與參數(shù)設(shè)置

本文選擇5組多峰基準(zhǔn)測試函數(shù)f1-f5和5組單峰基準(zhǔn)測試函數(shù)f6-f10來驗證算法性能。表2給出了測試函數(shù)的定義、搜索空間和理論最優(yōu)解。

表2 測試函數(shù)

表2(續(xù))

所有對比算法都統(tǒng)一設(shè)置種群大小為10，最大迭代次數(shù)為500。針對上述每個函數(shù)，每種算法均獨立運行30次。對比算法與參數(shù)設(shè)置見表3、表4。

表3 對比算法

表4 各算法參數(shù)設(shè)置

3.3 算法尋優(yōu)精度比較

所有測試函數(shù)的實驗結(jié)果見表5、表6。

從表5可以看出，對于多峰測試函數(shù)f1-f5：在函數(shù)f1、f4中，IHCA、TIHCA與WOA得到相同的最優(yōu)值；在函數(shù)f2、f3中，IHCA與TIHCA各項指標(biāo)的值非常接近，且均優(yōu)于其它算法；在函數(shù)f5中，IHCA的最差值、平均值、標(biāo)準(zhǔn)差均優(yōu)于其它對比算法。

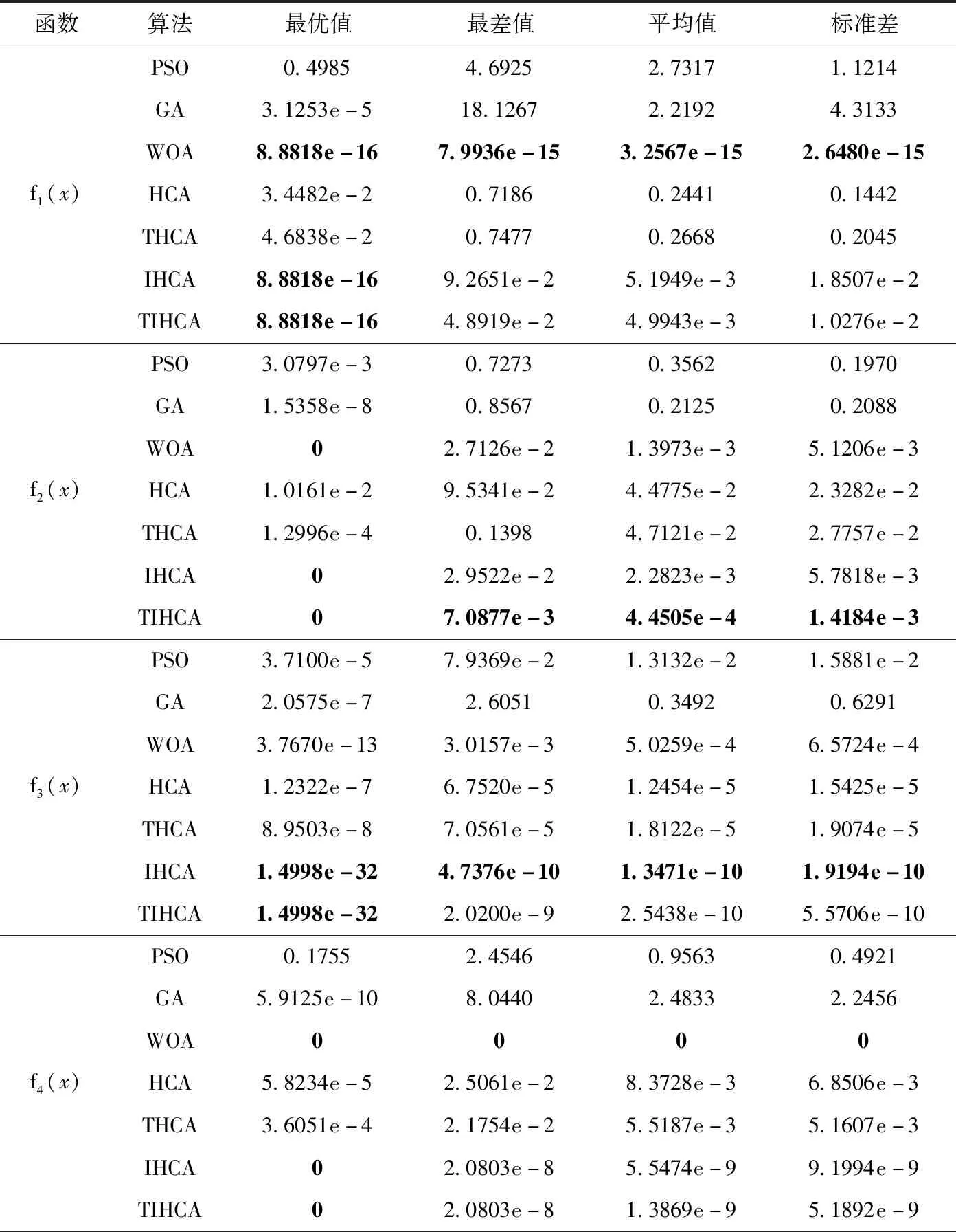
表5 多峰函數(shù)尋優(yōu)精度對比結(jié)果

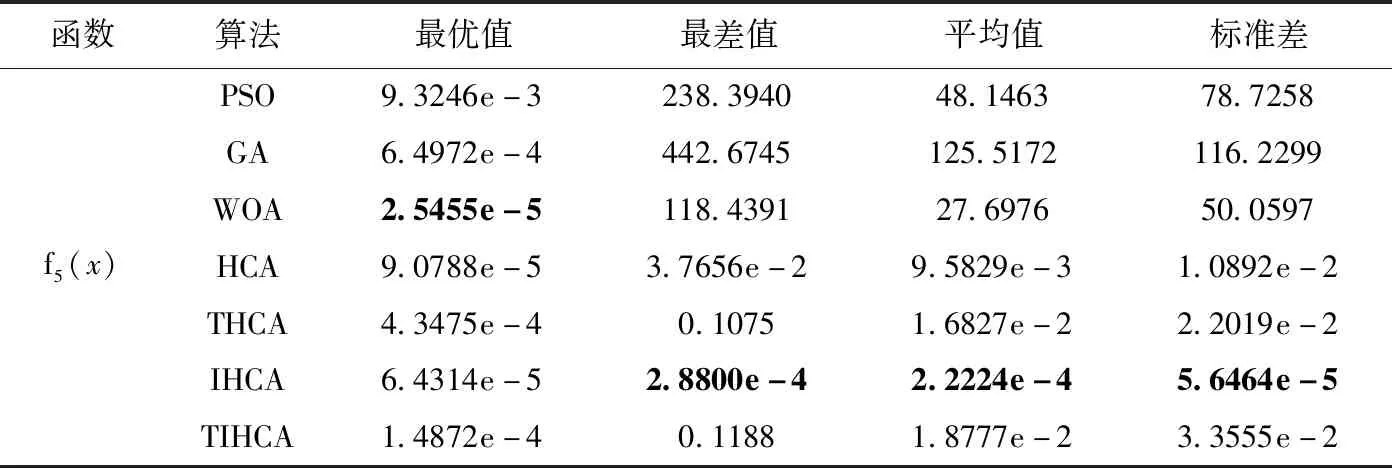
表5(續(xù))

從表6可以看出，對于單峰測試函數(shù)f6-f10：就函數(shù)f6、f7、f10而言，IHCA與TIHCA準(zhǔn)確找到理論最優(yōu)值，且表現(xiàn)穩(wěn)定；在函數(shù)f8中，IHCA與TIHCA得到相同的最優(yōu)值，但I(xiàn)HCA的最差值、平均值、標(biāo)準(zhǔn)差優(yōu)于TIHCA以及其它對比算法。

表6 單峰函數(shù)尋優(yōu)精度對比結(jié)果

與HCA相比，THCA有3個函數(shù)的平均值更優(yōu)，其余函數(shù)的平均結(jié)果相差不大；IHCA在10個函數(shù)中的尋優(yōu)均值均優(yōu)于HCA；TIHCA在9個函數(shù)中具有更好的平均值。總體而言，IHCA在尋優(yōu)精度方面表現(xiàn)最好，而 TIHCA 僅次于IHCA。這表明逆水流策略在尋優(yōu)精度上具有明顯優(yōu)勢，而自適應(yīng)溫度更新參數(shù)策略雖未能有效地改善HCA的尋優(yōu)精度，但減少流動階段的循環(huán)次數(shù)未對算法的尋優(yōu)精度造成不利影響。

3.4 算法收斂速度比較

各個算法針對不同函數(shù)的收斂曲線如圖3-圖12所示。

圖3 函數(shù)f1的收斂曲線

圖4 函數(shù)f2的收斂曲線

圖5 函數(shù)f3的收斂曲線

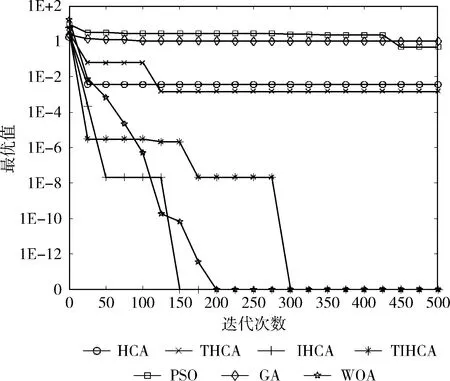
圖6 函數(shù)f4的收斂曲線

圖7 函數(shù)f5的收斂曲線

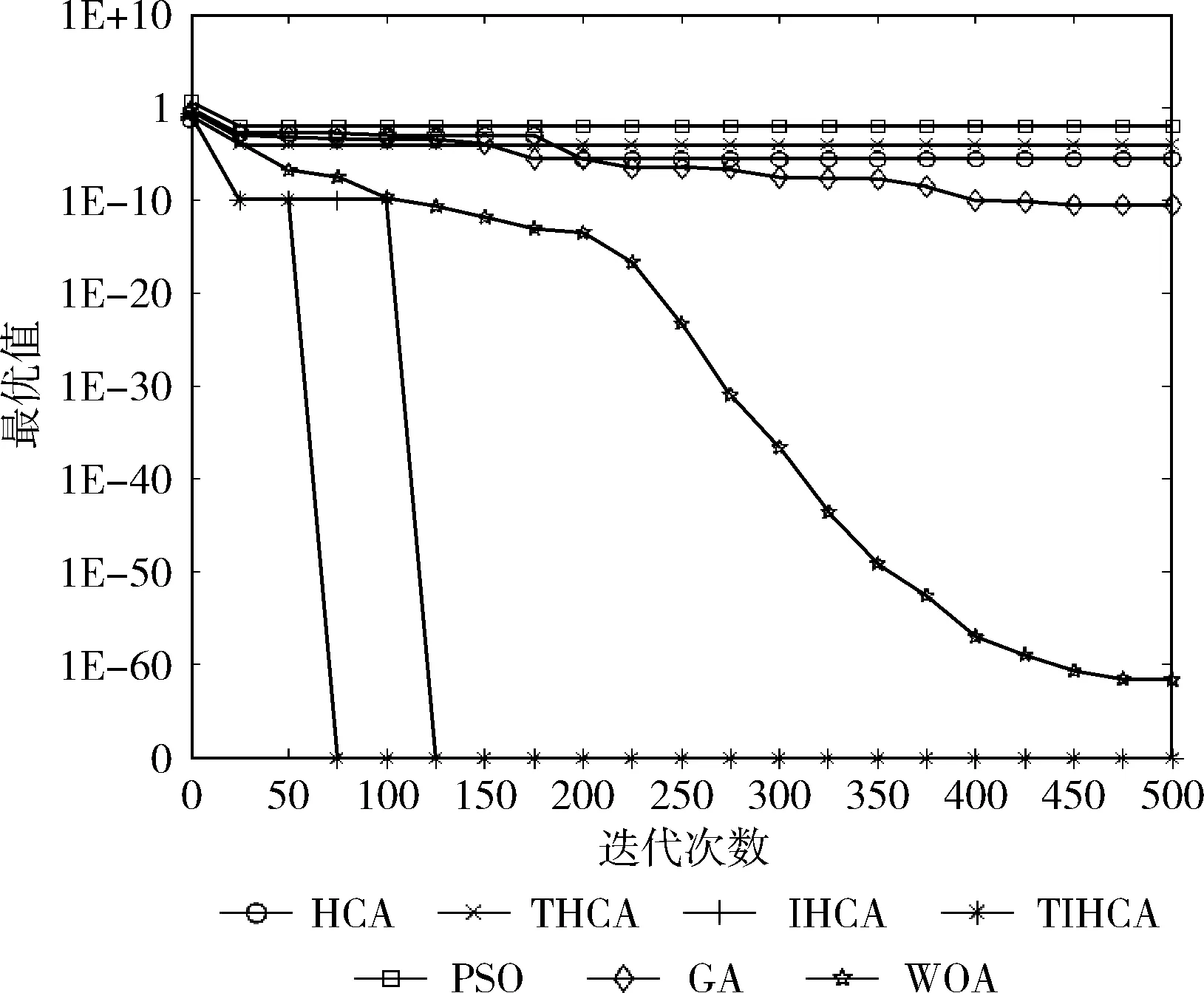
圖8 函數(shù)f6的收斂曲線

圖9 函數(shù)f7的收斂曲線

圖10 函數(shù)f8的收斂曲線

圖11 函數(shù)f9的收斂曲線

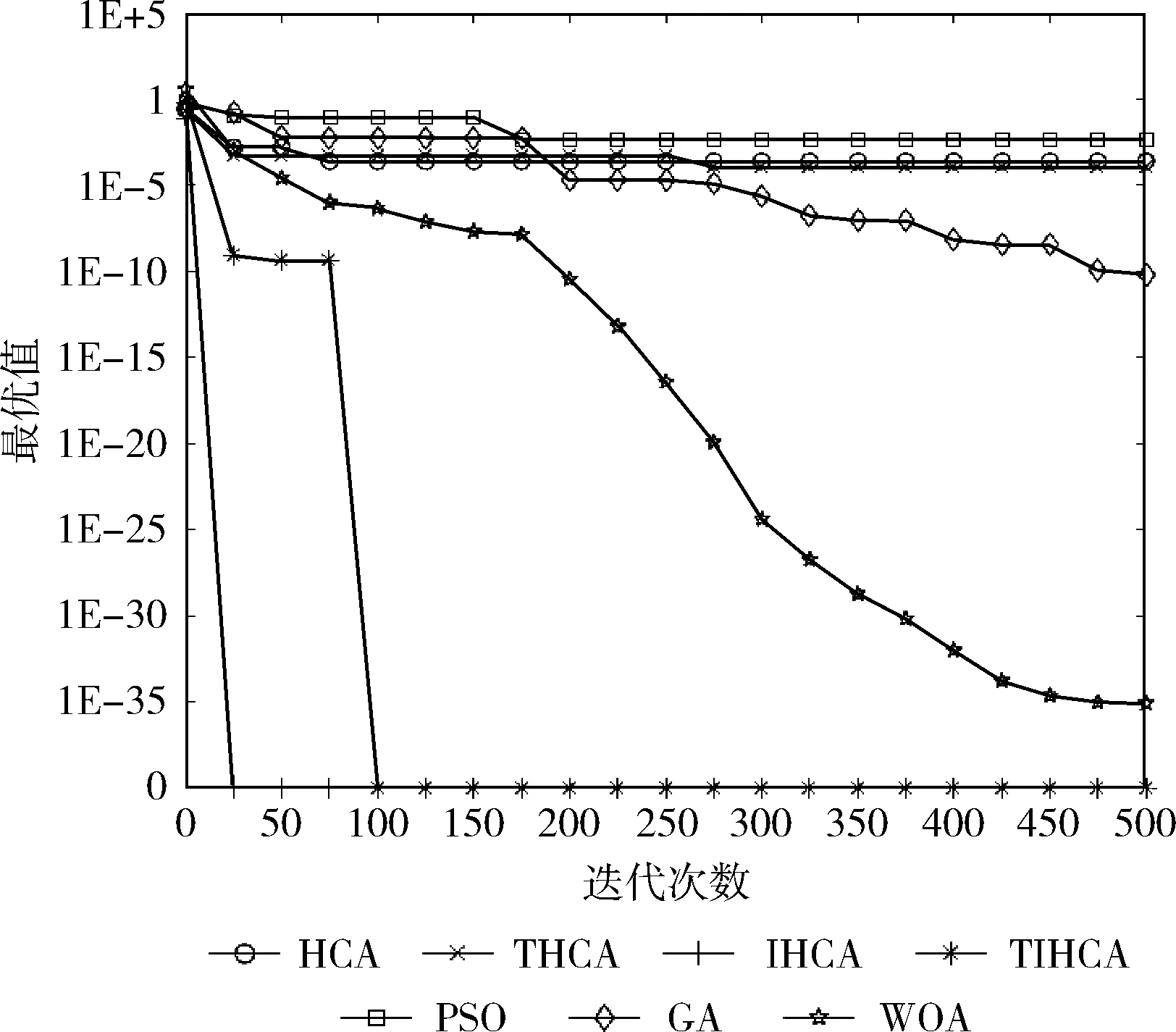
圖12 函數(shù)f10的收斂曲線

從圖中可以看出，在絕大多數(shù)時候，所有改進(jìn)的HCA都比HCA更快收斂。在函數(shù)f1-f3、f6中，THCA的收斂速度最快。雖然在函數(shù)f1、f2、f6中，PSO與THCA具有相同的收斂速度，但PSO的尋優(yōu)精度較差。在函數(shù)f7、f8、f10中，IHCA具有最快的收斂速度。雖然在函數(shù)f8中，GA與IHCA的收斂速度相同，但GA的尋優(yōu)精度遠(yuǎn)低于IHCA。在函數(shù)f9中，TIHCA的收斂速度最快。

與HCA相比，THCA在函數(shù)f1-f3、f5-f7、f9中具有更快的收斂速度，IHCA在函數(shù)f1、f3、f5-f8、f10中的收斂速度更快，TIHCA在函數(shù)f1、f2、f5、f6、f9中收斂更快。總體而言，THCA與IHCA的收斂速度最快。這表明各個策略對算法的收斂速度均有不同程度的提升，而混沌初始化與自適應(yīng)溫度更新參數(shù)的結(jié)合，以及混沌初始化與逆水流的結(jié)合在收斂速度上均有更好的改進(jìn)效果。

3.5 算法運行時間比較

對算法運行30次的時間取平均值，所有對比算法的運行時間如圖13所示。

圖13 f1-f10運行時間對比結(jié)果

從圖13可以看出，針對10個測試函數(shù)，PSO、GA與WOA的運行時間均為最短，這是由于HCA本身具有較多且復(fù)雜的參數(shù)與公式，即使改進(jìn)后的算法THCA、IHCA、TIHCA運行時間仍較PSO、GA與WOA更長。

與HCA相比，THCA在函數(shù)f1-f5、f7-f10上的運行時間更短，IHCA在函數(shù)f3-f5、f9上花費更少的時間，TIHCA在函數(shù)f3-f5、f7-f10上的運行時間更短。總體而言，THCA的運行時間最短，這體現(xiàn)了自適應(yīng)溫度更新參數(shù)策略在運行時間上的優(yōu)越性。而TIHCA僅次于THCA，這是由于逆水流過程的引入會增加一定的計算量。

綜合上述實驗結(jié)果可以看出：THCA的運行時間最短、收斂速度最快，IHCA具有最好的尋優(yōu)精度與收斂速度，而TIHCA折中了尋優(yōu)精度與運行時間兩方面的性能指標(biāo)，算法性能介于THCA與IHCA之間。在求解實際優(yōu)化問題時，可以根據(jù)實際需要選擇合適的策略。

4 結(jié)束語

針對水文循環(huán)算法的不足，本文采用混沌的方法初始化水滴種群，增強算法的全局搜索能力、提升算法的收斂速度；引入自適應(yīng)溫度更新參數(shù)策略，減少算法的運行時間；提出逆水流過程代替原凝結(jié)階段中的變異操作，以提高算法的尋優(yōu)精度。實驗結(jié)果表明，改進(jìn)的算法在收斂速度、尋優(yōu)精度與運行時間等方面均有較大的性能提升。然而，水文循環(huán)算法自身也存在局限性：算法中包含大量參數(shù)與動態(tài)變量，以致水文循環(huán)算法以及本文中的改進(jìn)算法在運行時間方面依然不如粒子群算法、遺傳算法與鯨魚算法，且求解高維函數(shù)較為困難。如何改進(jìn)這些缺點，將是下一步的研究工作。