基于Green 函數(shù)法的Timoshenko 曲梁強迫振動分析

趙 翔，周 揚，邵永波，劉 波，周 仁

(1. 西南石油大學(xué)土木工程與測繪學(xué)院，成都 610500；2. 西南油氣田分公司重慶氣礦開發(fā)科，重慶 400021)

我國基礎(chǔ)設(shè)施建設(shè)的不斷完善加快了土木工程、機械工程、石油工程等的發(fā)展步伐，在很多實際工程問題中，由于受場地、工程地質(zhì)條件以及優(yōu)化和美觀設(shè)計等影響，直梁結(jié)構(gòu)不再能滿足工程需求，因此出現(xiàn)了很多曲梁結(jié)構(gòu)，例如曲線橋梁、曲線隧道和彎曲機械構(gòu)件等[1 ? 3]。研究曲線結(jié)構(gòu)的抗震與直線結(jié)構(gòu)不同，它的力學(xué)特性復(fù)雜，分析起來更加困難[4]。在對這些實際工程問題的研究中，曲線結(jié)構(gòu)抗震研究往往被簡化為曲梁的強迫振動。許多學(xué)者已經(jīng)在做這方面的研究，例如魏雙科[5]建立雙脊骨空間模型用于分析曲線梁橋的地震反應(yīng)行為；閆磊等[6]提出了一種新型抗震體系—漂浮抗震體系，該抗震體系適用于非規(guī)則曲線橋梁的抗震；周彥良等[7]研究曲線隧道在不同地震波輸入方向下不同斷面的拱頂位移、內(nèi)力和最大主應(yīng)力變化規(guī)律；周彥良等[8]分析了曲線隧道的震害特性與機理。何燕麗、趙翔[9]建立了力電耦合的曲梁壓電俘能器模型并運用Green函數(shù)求得其強迫振動的解析解。

國內(nèi)外學(xué)者對曲梁的靜力學(xué)研究已經(jīng)比較成熟[10 ? 14]，針對Timoshenko 曲梁，Lee 和Yan[15 ? 16]應(yīng)用位移函數(shù)法對具有強非線性邊界條件的Timoshenko 曲梁的面內(nèi)、外靜撓度進行了研究。靜力法能解決簡單曲梁結(jié)構(gòu)與工況的位移及內(nèi)力分析問題，且可以獲得解析解，但對于復(fù)雜結(jié)構(gòu)、復(fù)雜工況，靜力法求解難度則比較大，所以對曲梁動力特性的研究顯得尤為重要。

梁的動力特性研究一直是一個經(jīng)典且長期存在的問題[4, 17 ? 18]。從以往的研究看，Euler、Rayleigh和Timoshenko 等各種各樣的經(jīng)典模型依次被提出。而曲梁的動力特性研究目前還處于探索階段，由于曲梁結(jié)構(gòu)在工程中的應(yīng)用日益增多，所以越來越多的學(xué)者開始關(guān)注曲梁的振動問題，而梁的振動分為自由振動和強迫振動，其中自由振動是指振動系統(tǒng)按其固有頻率振動，不需外力的作用，而強迫振動是指在周期性外力的持續(xù)作用下，振動系統(tǒng)發(fā)生的振動。目前來看針對Timoshenko曲梁強迫振動問題的研究還較少，多數(shù)的學(xué)者主要還是傾向于研究Timoshenko 曲梁的面內(nèi)、外自由振動。例如，Lee[19 ? 20]用偽譜法對Timoshenko曲梁進行面內(nèi)、面外自由振動分析，Liu[21]基于等幾何方法對Timoshenko 曲梁的面內(nèi)、外自由振動進行了研究，Lv 等[22]結(jié)合改進的傅里葉級數(shù)法和瑞利-里茲法，給出了具有一般彈性邊界和耦合條件的多跨Timoshenko曲梁面內(nèi)振動分析的統(tǒng)一解。當然還有一些研究方向不同的學(xué)者，例如，Calim[23]通過對空間彎曲和扭曲的Timoshenko 梁理論公式的重寫，得到了粘彈性地基上圓形梁的控制方程。

上述學(xué)者對Timoshenko 曲梁的振動問題做了很多研究，但其研究方向主要還是集中在自由振動的問題上。經(jīng)過作者的文獻調(diào)研，迄今為止還未有學(xué)者對Timoshenko 曲梁的強迫振動問題進行深入研究。由于結(jié)構(gòu)在地震荷載作用下的破壞主要源于強迫振動，因此研究曲梁的強迫振動問題對今后的曲梁結(jié)構(gòu)抗震分析是十分必要的。

從整體上看，以往的研究大多沒有考慮阻尼效應(yīng)。事實上，阻尼效應(yīng)在工程應(yīng)用中是非常重要的，Li 等[24]通過引入兩個特征參數(shù)來考慮阻尼對強迫振動的影響，用Green 函數(shù)法求解了Timoshenko 直梁在強迫振動下的解析解；本文在參考文獻[24]的基礎(chǔ)上研究了具有阻尼效應(yīng)的Timoshenko 曲梁(TCB)強迫振動的穩(wěn)態(tài)Green 函數(shù)。從基本控制方程出發(fā)，本文依次采用分離變量法和Laplace 變換，推導(dǎo)出Green 函數(shù)，其中涉及的所有常數(shù)由邊界條件決定。通過將某些物理量設(shè)置為零或無窮大，可以很容易地將目前的基本解簡化為不存在阻尼效應(yīng)的經(jīng)典Timoshenko 直梁 (TB)、 Prescott 梁 (PB)和 Euler-Bernoulli 梁(EB)的基本解。通過數(shù)值計算，討論了該方法的有效性，并給出了各種特殊幾何物理量的影響。目前的解決方案以封閉和顯式的形式給出，可以作為計算方法的基準。此外，根據(jù)最近的研究[25 ? 27]，本文可以利用現(xiàn)有的解決方案對更多涉及的問題進行分析。

1 TCB 模型的建立

曲梁強迫振動的控制振動方程[28]為：

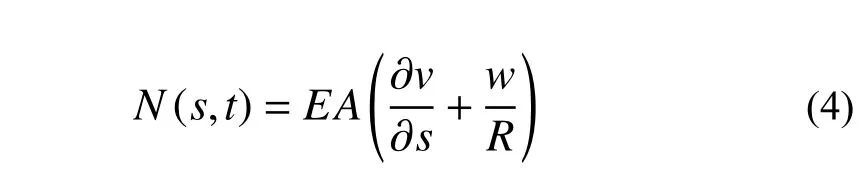
式中：v(s,t)、w(s,t)、ψ(s,t)分別為曲梁的軸向位移、徑向位移和轉(zhuǎn)角；p(s,t)為外部荷載；N(s,t)為軸向力；Q(s,t)為剪力；M(s,t)為彎矩；R、A、I分別表示曲梁的半徑、截面面積和截面靜距；E、G分別為曲梁材料的彈性模量和剪切模量；γ、μ分別表示曲梁的轉(zhuǎn)動慣量和單位長度質(zhì)量；κ為曲梁的剪切修正因子[29]；c1表示平動阻尼[30]；“.”表示對時間t的導(dǎo)數(shù)。

式中：EI和κAG分別代表彎曲剛度和剪切剛度；“'”表示對曲梁任意截面位置s的導(dǎo)數(shù)。假設(shè)梁上作用有如下簡諧分布荷載：

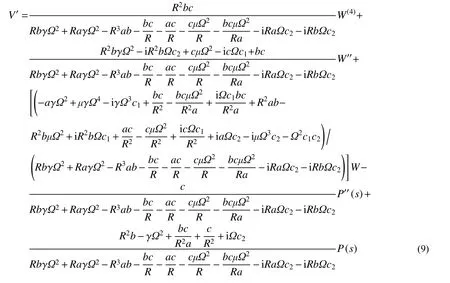
將式(8a)與式(8b)聯(lián)立消除Ψ，此時再將式(9)代入，即得到TCB 的振動控制方程：

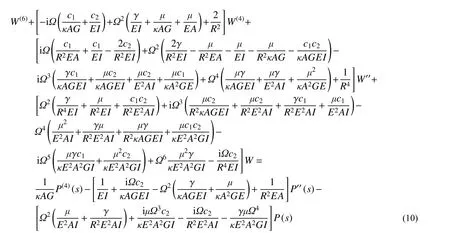
2 TCB 強迫振動的穩(wěn)態(tài)Green 函數(shù)

振動控制方程式(10)可以簡寫成以下形式：

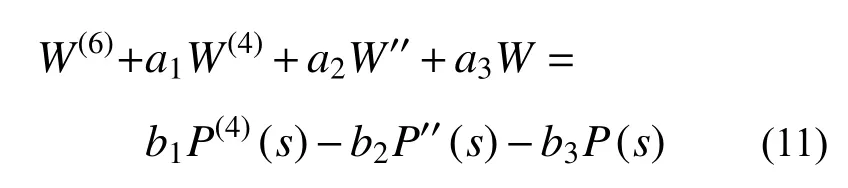
當常數(shù)a1、a2、a3、b1、b2和b3被賦予適當?shù)闹禃r，Euler-Bernoulli 曲梁(ECB)和Prescott 曲梁(PCB)的振動方程也可以表示為式(11)的形式。不同梁模型所對應(yīng)的a1、a2、a3、b1、b2和b3可見附錄1 中的表1。

值得注意的是式(10)可以被退化為經(jīng)典模型。在讓c1和c2消失的情況下，設(shè)置曲梁半徑R為無窮大可以得到不產(chǎn)生阻尼效應(yīng)的傳統(tǒng)TB 模型；如果進一步設(shè)置剪切修正因子κ為無窮大，就得到了PB 模型的控制方程；最后忽略轉(zhuǎn)動慣量的影響，也就是令γ=0 可以得到EB 模型的控制方程[21]。(注*：在下文中，作者引用變量 x 代替曲梁的任意截面位置 s ，以便于與Laplace 變換中的復(fù)變量s= σ +i τ 作區(qū)分)。

根據(jù)疊加原理，式(11)的解可以表示為如下卷積積分的形式：

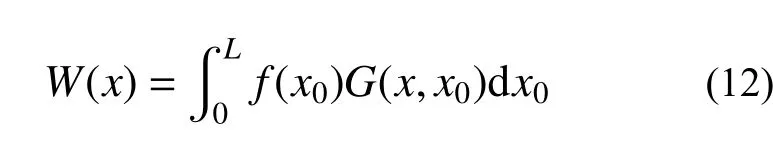
式中：L為梁的長度；f(x0)為外部荷載的分布函數(shù)；G(x,x0)為待求的Green 方程。從物理上來說，Green 方程G(x,x0) 指的是梁上任意一點x0作用一個單位集中力所引起的梁的響應(yīng)。從數(shù)學(xué)上來說，G(x,x0)指的是下面微分方程的解：

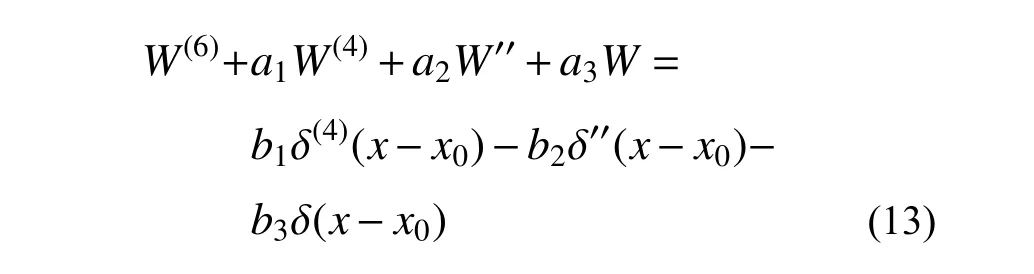
式中，δ(·)是狄拉克函數(shù)。由式(13)可以看出G(x,x0)=W(x,x0)，即在x=x0處作用一個簡諧單位集中力所引起的梁的位移W(x)。

為了推導(dǎo)出相應(yīng)的Green 函數(shù)，作者對式(13)中的變量x施行Laplace 變換，這里引入一個新的函數(shù)We(x)：

對式(13)中的變量x施行Laplace 變換，得到：

3 確定Green 函數(shù)的待定系數(shù)

首先通過計算 ?i(x) (i=1, 2, ···, 7)的各階導(dǎo)數(shù)，來確定常數(shù)W(0)、W'(0)、W"(0)、W"'(0)、W(4)(0)和W(5)(0)，根據(jù)式(16)中Ai(x)和式(19)中 ?i(x)的定義有：

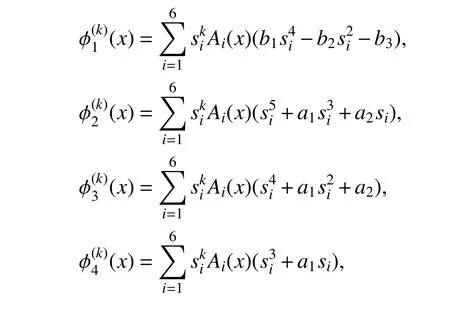
物理上來說，式(21)建立了邊界處x=0 與梁上任意截面位置x之間的關(guān)系，特別當x=L時，可以建立以下代數(shù)方程組：

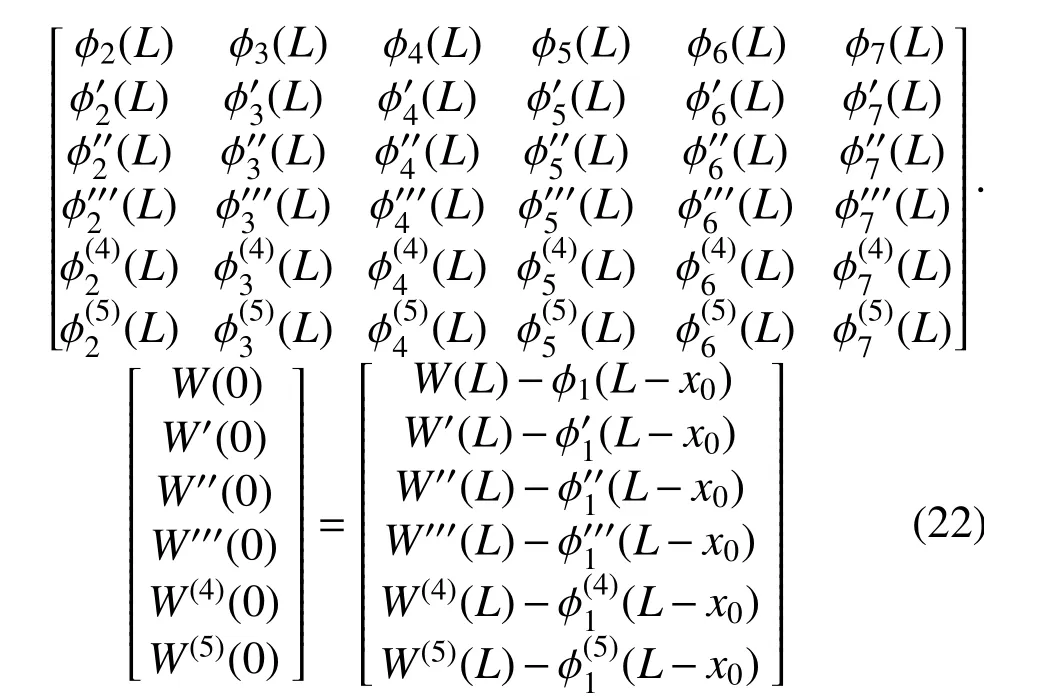
如果令?1(x)及其各階導(dǎo)數(shù)都為0，則式(22)所描述的關(guān)系同樣適用于TCB 的自由振動。

在確定了曲梁的邊界條件下，常數(shù)W(0)、W'(0)、W"(0)、W"'(0)、W(4)(0)和W(5)(0)可以被求解。對不同的梁模型：EB、PB 和TCB，各種不同邊界條件的表示形式參見附錄2 中表2。

本文解適用于附錄2 中的各種不同邊界，這里以兩端簡支的TCB 在x=L/2 處受到簡諧荷載P0cosΩt作用為例進行具體求解過程的說明，如圖1所示，來說明如何確定6 個待定常數(shù)：W(0)、W'(0)、W"(0)、W"'(0)、W(4)(0)和W(5)(0)。

首先，根據(jù)x=0 處的邊界條件確定位移和力學(xué)邊界：

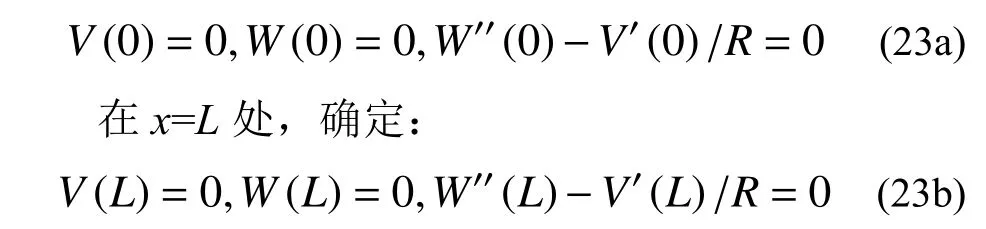
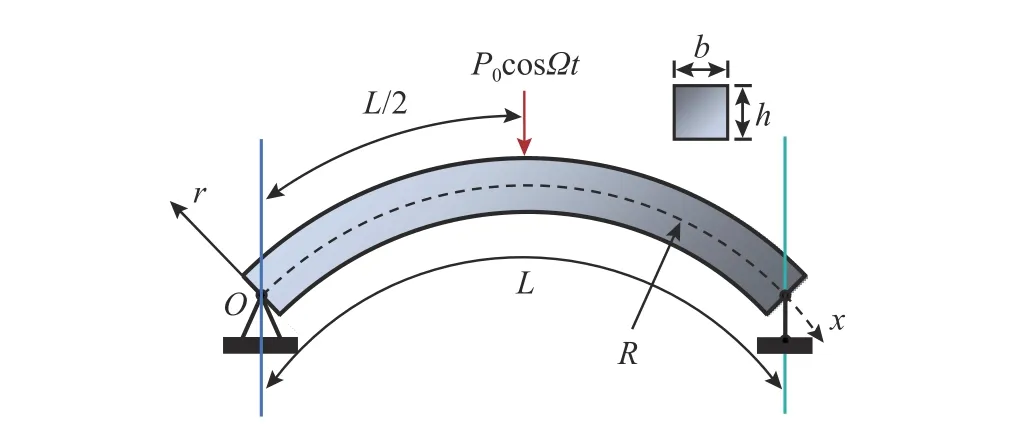
圖1 兩端簡支的曲梁在x=L/2 處受到簡諧力作用Fig. 1 A simply-supported curved beam subject to harmonic force at x=L/2

通過將位移邊界式(23)代入式(8)中通過消元法得到W(0/L)、W'(0/L)、W''(0/L)、W'''(0/L)、W(4)(0/L)和W(5)(0/L)的關(guān)系式：

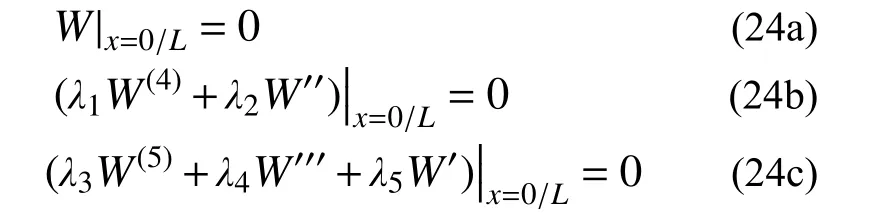
將其與式(21)聯(lián)立可得到如下矩陣：

左邊界處：x=0，此時有，W(0)=0，矩陣(25)中的前兩個方程由式(24b)和式(24c)得到；右邊界處：x=L，此時將式(21a)代入式(24a)，將式(21c)和式(21e)代入式(24b)，將式(21b)、式(21d)、式(21f)代入式(24c)，可依次得到矩陣式(25)中的后3 個方程。

λ1、λ2、λ3、λ4和λ5的值參見附錄4，從而式(21)中的所有常數(shù)W(0)、W'(0)、W"(0)、W"'(0)、W(4)(0)和W(5)(0)被確定。因此兩端簡支的TCB 的Green函數(shù)的形式如下：

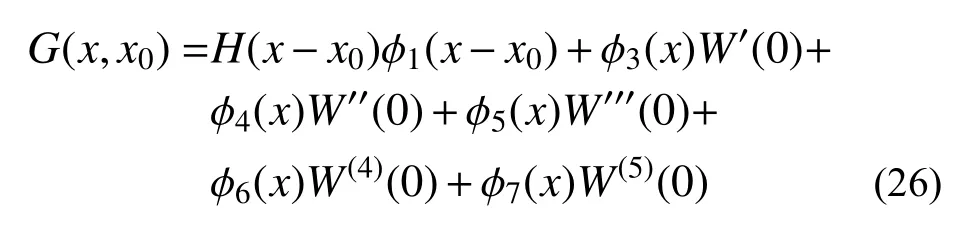
其中， ?i(x)(i=1, 3, 4, 5, 6, 7)在式(19)中被給出，應(yīng)該再次指出的是式(26)適用于TB、PB 和EB；通過將半徑R設(shè)置為無窮大，可以簡化為TB 振動模型，在此基礎(chǔ)上，將剪切修正因子κ設(shè)置為無窮大，可以退化為PB 振動模型，最后再把轉(zhuǎn)動慣量γ 設(shè)置為0，可退化為EB振動模型。

對于其它的邊界條件，如兩端固支，兩端自由，固支-簡支，懸臂等邊界條件，與求解兩端簡支曲梁的Green 函數(shù)一樣，按照同一過程也可以得到相應(yīng)的Green 函數(shù)。

4 數(shù)值結(jié)果和討論

如圖1 所示,考慮到一個兩端簡支的TCB，梁高為h，梁長L，在x0=L/2 處受到單位簡諧集中力P(x,t)=δ(x?L/2)eiΩt作用。為了便于說明，本文引入以下無量綱化參數(shù)：

4.1 Green 函數(shù)解的有效性驗證

在第3 節(jié)中，已經(jīng)提到TCB 模型的Green 函數(shù)解可以退化為TB 模型的Green 函數(shù)解。利用這一點可以對簡支TCB模型的Green 函數(shù)解進行退化驗證，看其是否與Li[24]所得到的TB 的Green函數(shù)解是一致的。因此如圖2 所示，作者將本文結(jié)果的退化解與文獻[24]中的簡支Timoshenko 直梁模型的結(jié)果作了對照。

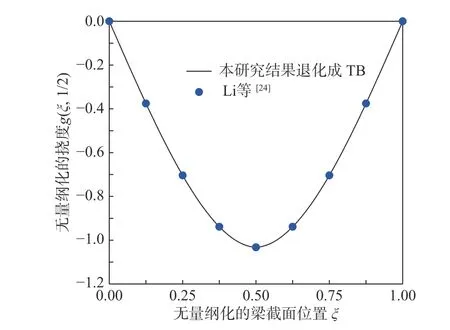
圖2 簡支TB 在中點處作用單位簡諧集中力的無量綱化的撓度Fig. 2 The dimensionless deflection subject to the external unit simple harmonic concentrated force at the middle section of simply supported TB

對照顯示，本文結(jié)果的退化解與文獻[24]的結(jié)果完全吻合，從而本文結(jié)果的有效性得到了驗證。

為了進一步驗證解的有效性，利用ANSYS 軟件建立了兩端固支的TCB 有限元模型，并將跨中處作用單位靜荷載下產(chǎn)生的無量綱化撓度與本研究的靜態(tài)解作對比分析，如圖3 所示。這里引入無量綱化參數(shù)：g1(ξ, ξ0)=G(x,x0)/wc，其中wc=L3/(192EI) 是兩端固支梁的中截面x0=L/2 處受到單位集中力作用產(chǎn)生的最大靜撓度。

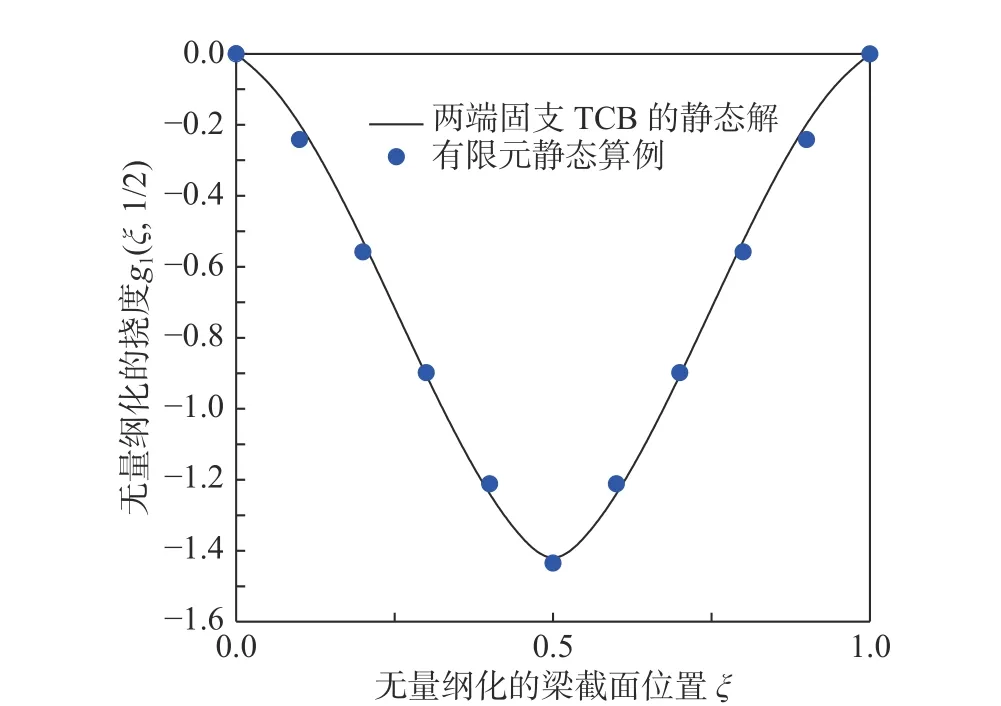
圖3 固支TCB 在中點處作用單位集中力的無量綱化的撓度Fig. 3 The dimensionless deflection subject to the external unit concentrated force at the middle section of fixed-fixed TCB

對比顯示本文的靜態(tài)解與有限元算例的位移值基本吻合，從而本文結(jié)果的有效性得到了進一步驗證。

4.2 兩端簡支的不同梁模型共振頻率研究

圖4 所示是以外激勵頻率Ω1為自變量的無量綱化撓度g(1/2, 1/2)，圖中的TB、PB、EB 均由TCB模型退化而得。

計算結(jié)果得出，當Ω1=1.0 時，EB發(fā)生共振。對于PB 和TB，它們的共振頻率分別為 ?P1B=0.997和 ?T1B=0.984，也就是說，其一階固有頻率分別為90.138 rad/s 和88.981 rad/s，這與文獻[21]中的結(jié)果一致，并且與文獻[36]中所預(yù)測的值相吻合，從而進一步證明了本文所得解的正確性。

圖5 所示是不同半徑的TCB(L=0.5m)以外激勵頻率Ω1為自變量的無量綱化撓度g(1/2, 1/2)。

從圖中可以看出，隨著半徑的增長，TCB的共振頻率逐漸減小，并收斂于TB(R=∞)的共振頻率。

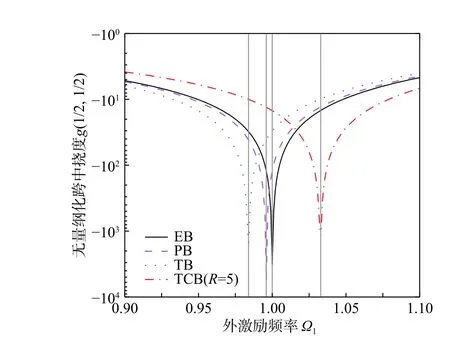
圖4 以外激勵頻率Ω1 為自變量的無量綱化撓度g(1/2,1/2)Fig. 4 The dimensionless deflection g(1/2, 1/2) as a function of the dimensionless frequency Ω1 of external dynamic force as independent variable

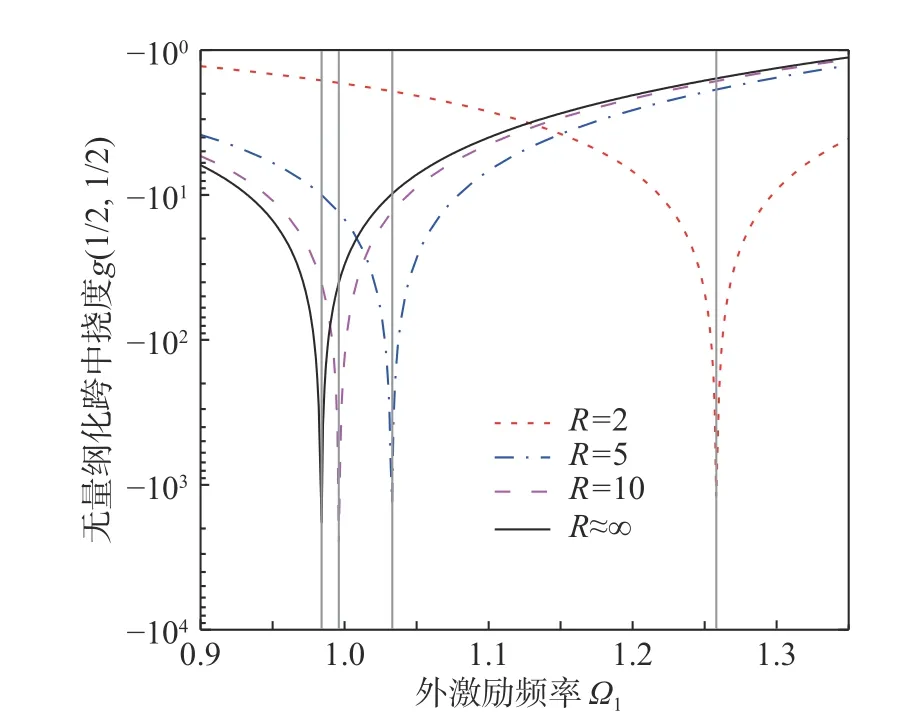
圖5 不同半徑的TCB 以外激勵頻率Ω1 為自變量的無量綱化撓度g(1/2,1/2)Fig. 5 The dimensionless deflection g(1/2, 1/2) as a function of the dimensionless frequency Ω1 of external dynamic force as independent variable for TCB with different radiuses

圖6 所示是無量綱化的梁的撓曲線g(ξ, 1/2)，其橫坐標是無量綱化的梁的跨度ξ=x/L。圖中的TB、PB、EB 均由TCB 模型退化而得。從四種梁模型相應(yīng)Green 函數(shù)曲線的模態(tài)形狀可以看出，Ω1=0.5 可以激發(fā)一階模態(tài)。在該頻率激勵下，PB與EB 的解極為接近，這說明轉(zhuǎn)動慣量對Green 函數(shù)的影響較為微弱。相反的，TB 與EB 的解差異顯著，這說明剪切效應(yīng)對梁的振動撓曲線影響較大。如圖6 所示，TCB 與三種直梁模型的撓曲線相似，其撓度比TB 模型的撓度小。但是從下一小節(jié)的研究結(jié)果中不難發(fā)現(xiàn)隨著半徑R的變小，TCB 的撓曲線形狀會發(fā)生較大的變化。

4.3 不同半徑下簡支TCB 的撓度變化

圖7 所示是不同半徑的TCB 無量綱化的撓曲線g(ξ, 1/2)，其橫坐標是無量綱化的梁的跨度ξ=x/L。

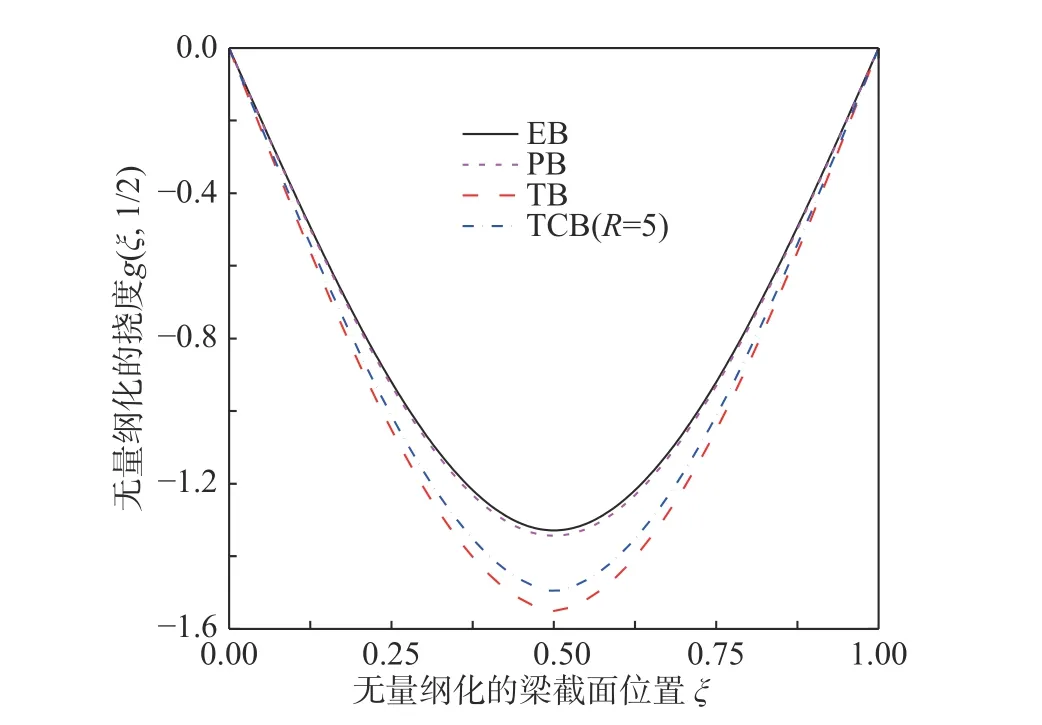
圖6 在外激頻Ω1=0.5 作用下，EB、PB、TB 和TCB(R=5)的無量綱化撓度g(ξ,1/2)Fig. 6 The dimensionless deflection g(ξ,1/2) of EB, PB, TB,and TCB (R=5) corresponding to Ω1=0.5 of external dynamic force.

圖7 不同半徑下，TCB 的無量綱化撓度g(ξ,1/2)Fig. 7 The dimensionless deflection g(ξ,1/2) of TCB with different radiuses

從圖中可以看出，隨著半徑R的減小，TCB的撓度逐漸變小，應(yīng)當特別指出的是：當半徑R=0.25 m 為梁長L=0.5 m 的1/2 時，其邊界處轉(zhuǎn)角為0，撓曲線的形狀類似于兩端固支的直梁。

圖8 所示是以半徑R為自變量的無量綱化撓度g(1/2, 1/2)。

圖中可以看出隨著半徑R的增長，在起始階段TCB 的跨中撓度呈線性增加，隨后增加趨勢逐漸變得緩和，最終收斂于相同條件下TB 模型的無量綱化撓度。

4.4 阻尼效應(yīng)對簡支TCB 的影響

圖9 與圖10 所示是以半徑R=2 m，梁長L=0.5 m的TCB 為例，分別以阻尼比ζ1和ζ2為自變量的無量綱化位移g(1/2, 1/2)。

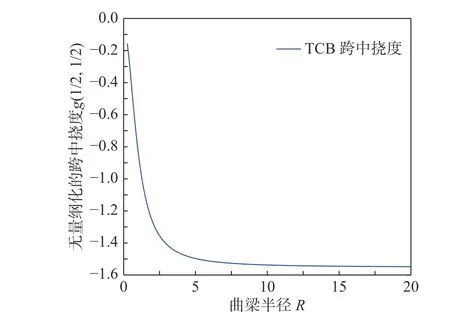
圖8 以半徑R 為自變量的TCB 的無量綱化撓度g(1/2,1/2)Fig. 8 The dimensionless deflection g(1/2,1/2) of TCB with radius R as independent variable

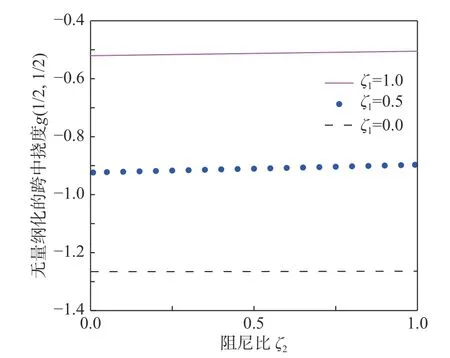
圖10 以阻尼比ζ2 為自變量的無量綱化撓度g(1/2, 1/2)Fig. 10 The dimensionless deflection g(1/2,1/2) of TCB with damping ratio ζ2 as independent variable

從圖中可以看出：隨著阻尼比ζ1和ζ2的增加，位移值變得越來越小，這是符合客觀物理實際的；另外，通過對比圖9 與圖10 還可以看出平動阻尼的影響比轉(zhuǎn)動阻尼要大。控制方程中的平動阻尼代表空氣阻尼，而轉(zhuǎn)動阻尼代表材料阻尼[33]。計算結(jié)果表明，材料阻尼對簡支曲梁的位移響應(yīng)影響較小，因此可以忽略。

5 結(jié)論

本文通過Laplace 變換，系統(tǒng)地研究了兩端簡支、固支、自由邊界條件下TCB 強迫振動的Green函數(shù)。并以兩端簡支邊界條件為例，證實了所得到的TCB 強迫振動Green 函數(shù)可以退化到TB、EB和PB 的強迫振動Green 函數(shù)。并通過數(shù)值手段，研究了以上四種梁模型的共振頻率、不同半徑下TCB 的撓度變化和阻尼效應(yīng)的影響。并得出以下幾點重要結(jié)論：

(2)隨著半徑R的增大，TCB 的無量綱撓度逐漸變大，并最終收斂于TB 的無量綱撓度，應(yīng)當特別指出的是：當半徑R=0.25 m 為梁長L=0.5 m 的1/2 時，其邊界處轉(zhuǎn)角為0，撓曲線的形狀類似于兩端固支的直梁。

(3)隨著阻尼比ζ1和ζ2的增加，TCB 的跨中撓度近似于線性越小。此外，由于材料阻尼對簡支曲梁的位移響應(yīng)影響較小，因此可以忽略。

在解的驗證部分，所得到的TCB 的Green 函數(shù)退化為TB 的Green 函數(shù)后與Li 等[24]所得到的TB 的Green 函數(shù)完全吻合，且退化為EB 的Green函數(shù)與Abu-Hilal[33]所得到的EB 的Green 函數(shù)一致。此外，本文的靜態(tài)解與有限元算例的位移值基本吻合，從而本文結(jié)果的有效性得到了進一步驗證。

本文的研究結(jié)果可為相關(guān)理論研究和工程應(yīng)用提供有益參考，文中所涉及的物理量符號說明參見附錄3 中表3。