采用粘彈性人工邊界單元時顯式算法穩定性分析

李述濤，劉晶波，寶 鑫，陶西貴，陳一村，肖 蘭，賈藝凡

(1. 清華大學土木工程系，北京 100084；2. 軍事科學院國防工程研究院，北京 100036)

采用數值方法計算土-結構地震反應或近場波動問題時，需要從半無限介質中切取出有限的近場區域進行計算，同時需在截斷邊界處設置人工邊界來模擬外行散射波向無窮遠的輻射效應[1 ? 4]。較為常見的粘彈性人工邊界[5]計算精度較高但前處理操作較為復雜，需遍歷所有邊界節點施加彈簧-阻尼器系統，在此基礎上發展了粘彈性人工邊界單元技術[6 ? 7]，它是沿邊界法線向外延伸的一層單元，通過賦予該層單元等效物理參數即可模擬粘彈性人工邊界對于外行散射波的吸收作用。由于該方法具有良好的計算精度和魯棒性，且前處理過程簡單，在實際工程計算中得到較多的應用[8 ? 12]。

隨著人工邊界技術的不斷發展，針對人工邊界條件的穩定性研究逐漸得到重視[13 ? 14]，目前針對此類問題的主要研究方法包括：Trefethen 等[15]提出的GKS 定理—基于偏微分方程初邊值問題有限差分格式的穩定性理論，給出初邊值問題多層線性差分格式穩定的充要條件；Liao 等[16]研究了離散模型中穩態波動的完備解，給出了多次透射邊界的穩定性條件；Kamel 等[17]和關慧敏等[18]通過傳遞矩陣譜半徑分析積分格式的穩定性。理論研究表明，如果不全面考慮逐步積分過程中人工邊界節點與內部節點運動方程的耦合效應，穩定性準則可能會失效。

由于粘彈性人工邊界或粘彈性人工邊界單元本身均為物理上穩定的系統，將其引入計算系統中，并不影響整體的物理穩定條件。但采用顯式時域逐步積分方法進行計算時，受粘彈性人工邊界單元粘性阻尼、剛度及幾何尺寸的影響，整體計算模型的數值積分穩定性條件將發生改變，目前尚未給出明確而實用的含粘彈性人工邊界條件影響的顯式算法穩定性準則，影響了數值分析時穩定時間步長的判斷和選取，進一步限制了粘彈性人工邊界單元在顯式動力分析中的應用。因此目前在引入粘彈性人工邊界單元進行波動問題分析時，多采用隱式的無條件穩定的時域逐步積分算法，以避免顯式算法帶來的數值穩定性問題。隱式算法需要求解聯立方程組，計算效率不高，并不適合大規模波動問題計算。隨著顯式時域逐步積分算法在工程結構和大范圍場地分析問題中的廣泛應用[19 ? 22]，有必要對含有粘彈性人工邊界單元的系統進行顯式時域逐步積分算法穩定性研究。

本文考慮人工邊界和內部單元節點的運動耦合效應，利用傳遞矩陣的譜半徑分析時域逐步積分格式(中心差分)的穩定性，給出不同位置處局部節點系統顯式時域逐步積分算法穩定條件的解析解，通過各子系統穩定性條件及內部介質穩定性條件的對比分析，給出考慮粘彈性人工邊界條件影響的整體耦合系統顯式時域逐步積分算法的穩定性條件。

1 粘彈性人工邊界單元等效物理參數及尺寸設置

粘彈性人工邊界單元是在模型截斷邊界處沿法線向外延伸的一層單元(見圖1)，人工邊界單元的厚度為h，質量密度為0，單元最外層節點固定。通過賦予單元等效物理參數來模擬粘彈性人工邊界。二維粘彈性人工邊界單元等效彈性模量、等效泊松比和等效阻尼系數分別為[2]：

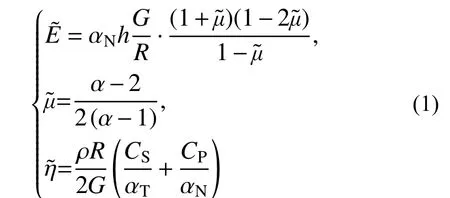
圖1 人工邊界單元尺寸示意圖Fig. 1 Artificial boundary elements size diagram

其中：設G為內部介質剪切模量； ρ為介質質量密度；CS和CP分別為介質S 波和P 波波速；R為散射波源至邊界節點的距離； α=αN/αT， αT與 αN分別為切向與法向粘彈性人工邊界參數，對于二維粘彈性人工邊界，其推薦值分別為0.5 和1，根據式(1)，此時為0。

盡管粘彈性人工邊界單元等效剛度矩陣的推導過程引入了邊界單元厚度h遠小于寬度L的假設，如圖1 所示，劉晶波等[6]和谷音等[7]通過進一步的研究表明，邊界單元厚度的魯棒性良好，可靈活取值而對精度影響很小。由于顯式算法的穩定條件受模型中的最小單元尺寸制約，在實際計算分析中，建議將邊界單元的寬度設定為與內部單元尺寸一致，以排除邊界單元尺寸對整體穩定性的影響，如圖2 所示。此時粘彈性人工邊界單元等效彈性模量、等效剪切模量可以寫為：

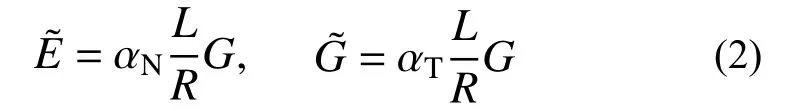
圖2 適用于顯式算法的人工邊界單元Fig. 2 Artificial boundary elements adapted to explicit algorithms

使用通用有限元軟件對粘彈性人工邊界單元賦予材料參數時，由于是各向同性介質，輸入等效彈性模量即可。另外還包括式(1)計算得到的等效阻尼系數，以及泊松比(=0)和質量密度(=0)。由于大多數軟件不支持將密度設為0，可采用近似0 的小數代替。

2 顯式時域逐步積分算法穩定性分析方法

時域逐步積分算法穩定性分析的目的是獲得時域逐步積分計算時滿足穩定性要求的時間離散步長 ?t。最大的穩定時間步長 ?t與單元的尺寸和系統的物理性質有關。為此在進行穩定性分析時，通常采用均勻介質和均勻離散化網格模型，如圖3 所示。

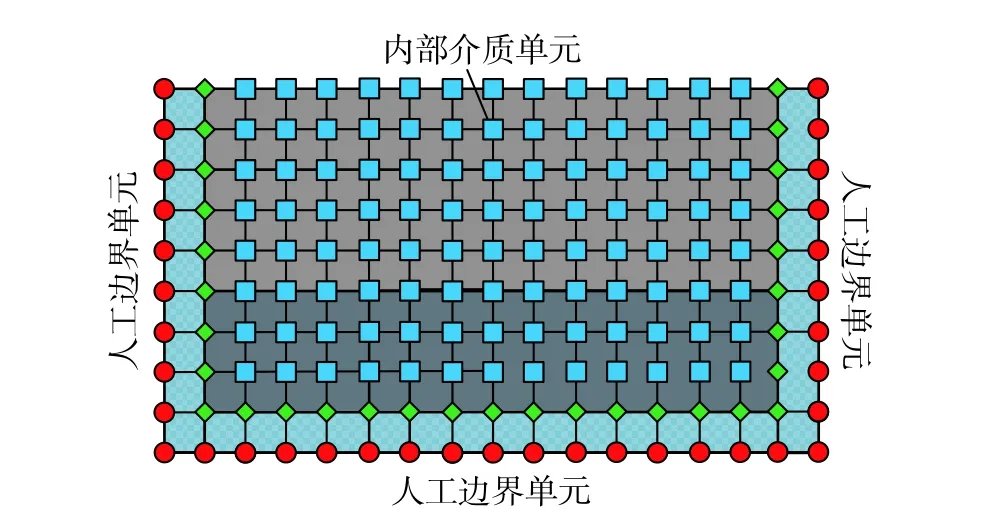
圖3 均勻離散化網格模型Fig. 3 Uniform discretization mesh model

當實際力學模型介質非均勻，單元尺寸不相同時，可以根據最小尺寸的單元或綜合考慮單元尺寸及其介質性質來確定整體計算模型的穩定離散時間步長 ?t。算法的穩定性通常可采用以下幾種分析方法：

① 不考慮自由邊界和人工邊界的影響，取無限計算區域模型，采用馮諾依曼方法進行穩定性分析。這一方法可以獲得內部系統的數值計算穩定條件，但無法考慮含人工邊界條件時系統的穩定性。

② 取實際的計算模型，考慮人工邊界的影響，通過對整體系統時域逐步積分方法的傳遞矩陣進行特征值分析，以獲得考慮耦合人工邊界條件影響的整體系統的數值計算穩定性條件。但由于涉及到整體模型傳遞矩陣的建立和分析，這一方法在實際工作中通常是不可行的，特別是對大規模的計算問題。

③ 為對透射人工邊界的數值計算穩定性進行有效分析，Kamel 等[17]和關慧敏等[18]提出了一種對含透射人工邊界條件子系統的傳遞矩陣進行特征值分析，以獲得波動問題中透射人工邊界穩定性的分析方法。由于分析中采用的子系統為沿人工邊界切向(寬度方向)上若干排節點和沿法向(深度方向)上若干排節點組成的節點系，子系統自由度較多，僅能靠數值方法對人工邊界的穩定性進行分析和判斷，未給出具有解析形式的更易于使用的人工邊界穩定性準則。

從以上有限元離散模型數值積分穩定性準則的研究工作中可以發現以下兩個特點：1)算法的穩定性與模型的截止頻率(系統最高階自振頻率)有關。2)截止頻率相應的振型呈現局部節點系相鄰節點交錯振動的形態。由以上兩個特點可以判斷，整體系統的截止頻率可通過對局部子系統模型的分析得到，進一步可通過局部子系統模型的數值穩定性分析，獲得整體系統的數值穩定性條件。

首先以一維剪切梁問題為例證明以上判斷。圖4 為一維剪切梁的離散模型及最高階振型示意圖，梁的剪切模量為G，密度為 ρ，橫截面面積為A，單元長度為L。取兩個子系統進行分析。子系統a：取振型兩節點之間的子系統，兩端施加約束，由于約束是施加于振型節點(振幅為零)之上，因此并不改變剪切梁有限元模型的自振頻率，如圖5(a)所示；子系統b：取兩個單元，在兩端施加約束，此時子系統的自振頻率與原系統的截止頻率不相同，如圖5(b)所示。

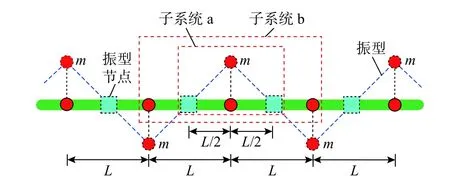
圖4 一維剪切梁振動示意圖Fig. 4 One-dimensional shear beam vibration diagram

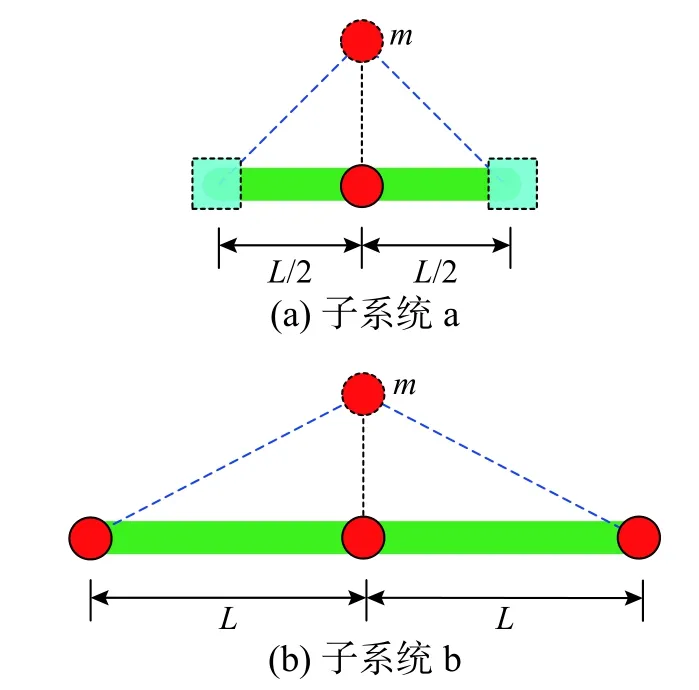
圖5 一維局部子系統Fig. 5 One-dimensional local subsystem

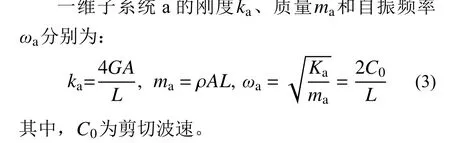
根據子系統的剛度和質量，可以建立子系統a的單自由度運動方程，當采用中心差分法進行時域逐步積分計算時，一維子系統a 的數值穩定條件為：

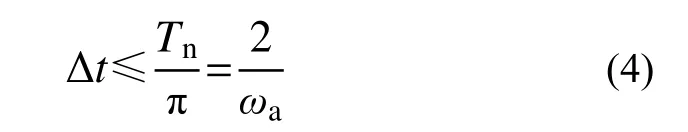
其中，Tn為子系統的自振周期，將式(3)中第三式代入式(4)，得到子系統數值積分穩定性條件為：

式(5)即為一維連續介質波動有限元分析時中心差分算法的穩定性條件，可見采用子系統a 獲得的局部穩定性條件即為連續介質整體模型的穩定性條件。

一維子系統b 的剛度kb、質量mb、自振頻率ωb和中心差分穩定性條件分別為：

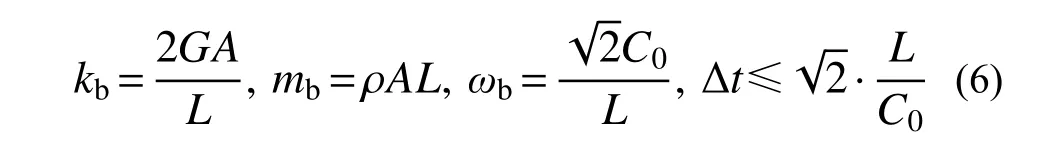
對比式(5)和式(6)，可以發現一維子系統b的穩定性條件比實際整體模型的穩定條件更為寬松，但仍然可以給出穩定時間積分步長 ?t的一個上限估計。

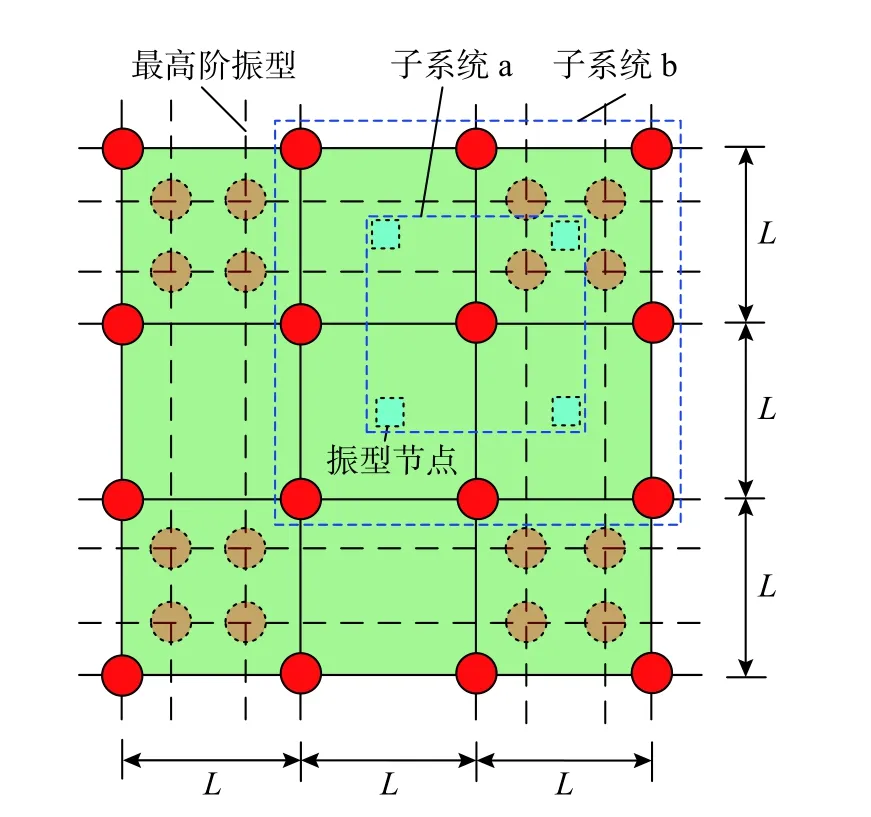
圖6 二維節點系統最高階振型圖Fig. 6 Highest-order modal pattern of two-dimensional nodes system

同樣取兩個子系統進行分析，二維問題局部子系統由4 個單元構成，如圖7(a)和圖7(b)所示。其中二維子系統a 的4 個角點為振型節點，位移為0，4 個邊點的位移條件可由振型和4 邊形等參元的性質確定，子系統a 對應的邊界條件為：

圖7 二維局部子系統Fig. 7 Two-dimensional local subsystem

二維子系統a 自振頻率和中心差分穩定條件為：

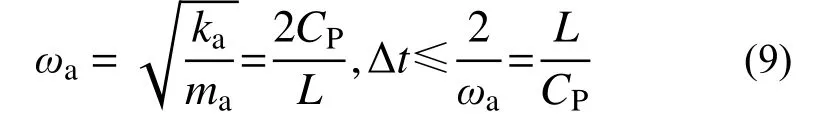
式(9)即為二維波動問題有限元分析時中心差分算法的穩定性條件，可見同樣可以由子系統a的局部穩定性分析獲得二維有限元模型數值算法的整體穩定性條件。

二維子系統b 由4 個單元構成，在周邊節點施加固定約束，子系統b 運動方程為：

同樣，二維子系統b 給出了整體有限元模型穩定時間積分步長的上限估計。

一維和二維子系統分析的結果表明：1)若能較為準確地判斷系統截止頻率對應的振動模態(振型)，則可以利用最高振型的特點和振型節點的分布規律，從整體系統中分離出由陣型節點所包圍的局部子系統，對振型節點施加約束條件，然后對該子系統進行穩定性分析，獲得的局部子系統穩定性條件即為整體模型的數值穩定條件；2)若不能準確判斷截止頻率對應振動模態和相應振型節點的位置，也可選取一個能體現整體有限元模型特征的最小的子系統，對該子系統的邊界節點施加約束，通過分析獲得子系統的數值穩定性條件，從而獲得整體系統穩定性判據中各物理量的關系式，且該條件是整體系統穩定性條件的一個逼近。再通過擴展數值算例進行修正，確定合適的系數，即可得到整體系統的數值積分穩定性條件。

當采用粘彈性人工邊界單元時，內部系統的數值穩定條件已知，但難以確定人工邊界區截止頻率對應的振型，因而僅能采用類似于b 型的子系統進行數值計算的穩定性分析。

對非均質子系統進行穩定性分析時，可根據顯式逐步積分算法格式，將系統運動方程寫成如下形式：

積分格式的穩定性問題與外力向量Qp無關。如果滿足下列兩條件，則積分格式(12)是穩定[23]：條件1： ρ(A)≤1 ， ρ(A)是傳遞矩陣A的譜半徑，即ρ(A)=max|λi|；條件2：如果A具有多重特征值，則該特征值的模小于1。因而可將子系統的穩定性分析歸結為傳遞矩陣A的形成及譜半徑計算，按上述條件即可建立穩定性準則。

3 人工邊界子系統穩定性分析

采用粘彈性人工邊界單元時，人工邊界區的子系統有兩種形式，一種在側面或底面切取，如圖8 所示，另一種在角點處切取，切取邊界可設置固定邊界(見圖9)或自由邊界(見圖10)。

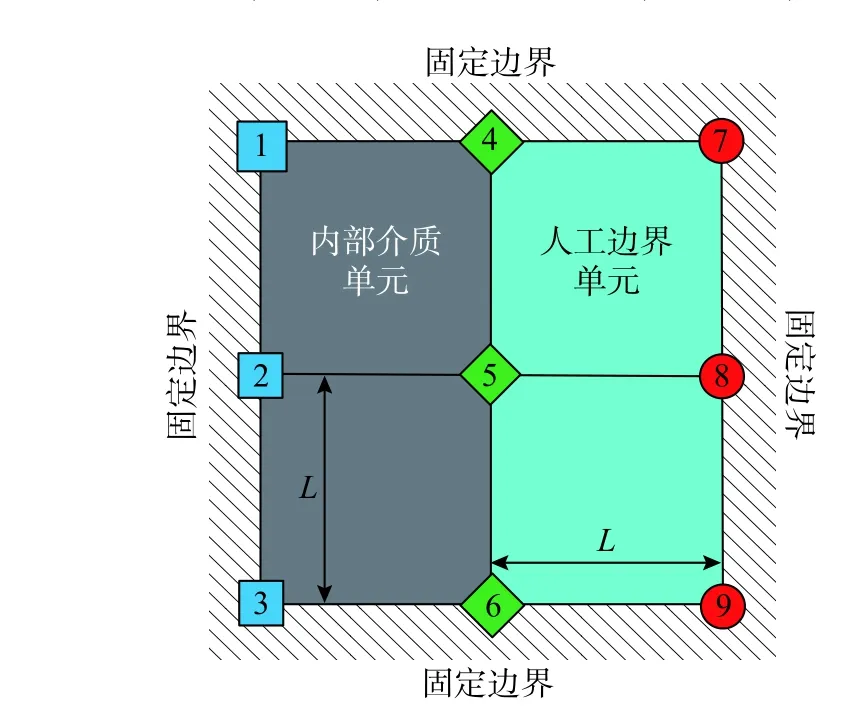
圖8 側邊固定邊界子系統Fig. 8 Side fixed boundary subsystem

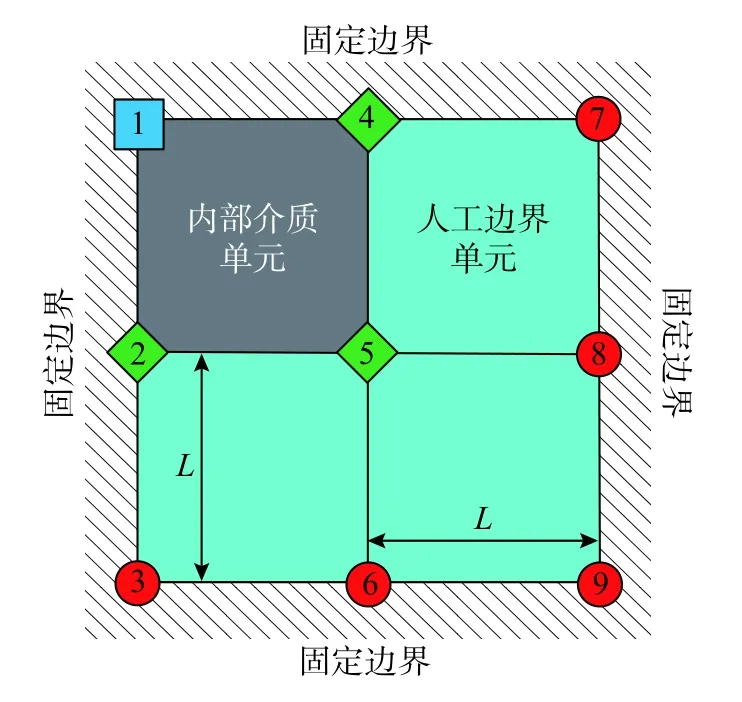
圖9 角點固定邊界子系統Fig. 9 Corner fixed boundary subsystem

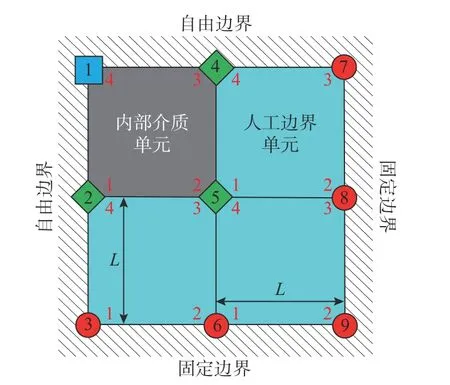
圖10 角點自由邊界子系統Fig. 10 Corner fixed boundary subsystem

3.1 側邊固定邊界子系統穩定性分析

側邊固定邊界子系統由兩個粘彈性人工邊界單元和兩個內部介質單元組成，如圖8 所示。設內部介質單元的彈性模量為E，剪切模量為G，密度為 ρ，泊松比為μ，且無阻尼；粘彈性人工邊界單元彈性模量為，阻尼系數為，泊松比為0，密度為0，單元邊長均為L。四節點正方形平面單元的集中質量矩陣、剛度矩陣、阻尼矩陣分別見文獻[6]和文獻[24]，按節點編號進行矩陣組裝后得到子系統中5 號節點運動方程如下：

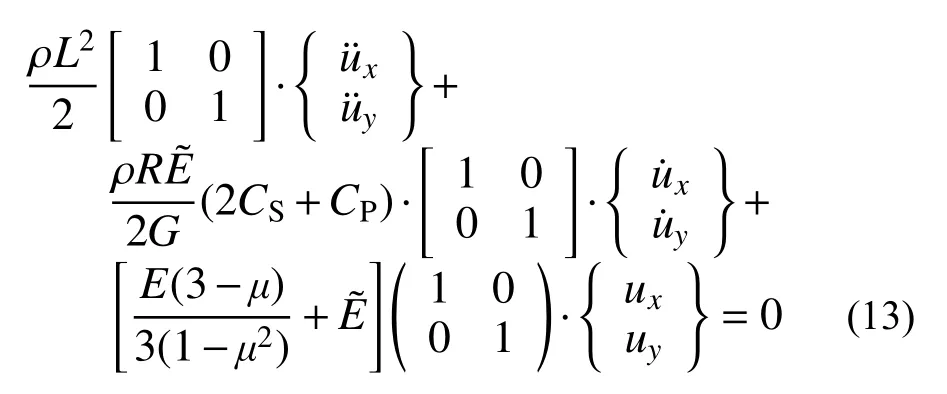
觀察式(13)可知，x和y方向運動方程是解耦的且形式相同，因此可只對其中一個方向的運動方程進行穩定性分析。顯式時域逐步積分格式(中心差分[25]如下：

式(19)即為側邊局部人工邊界子系統穩定性條件的解析表達形式，觀察可知該子系統的穩定性條件與內部介質壓縮波速、泊松比、單元尺寸和模型大小有關。

3.2 角點固定邊界子系統穩定性分析

角點處固定邊界子系統中由3 個粘彈性人工邊界單元和1 個內部介質單元組成，如圖9 所示。將四節點正方形平面單元質量、阻尼和剛度矩陣按節點編號組裝后得到5 號節點的運動方程如下：

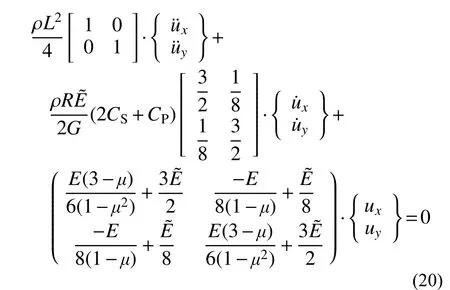
由于該運動方程的坐標耦聯，需對整體方程進行穩定性分析。將式(1)代入式(20)，然后根據式(14)將式(20)展開，寫成如下傳遞矩陣的形式：

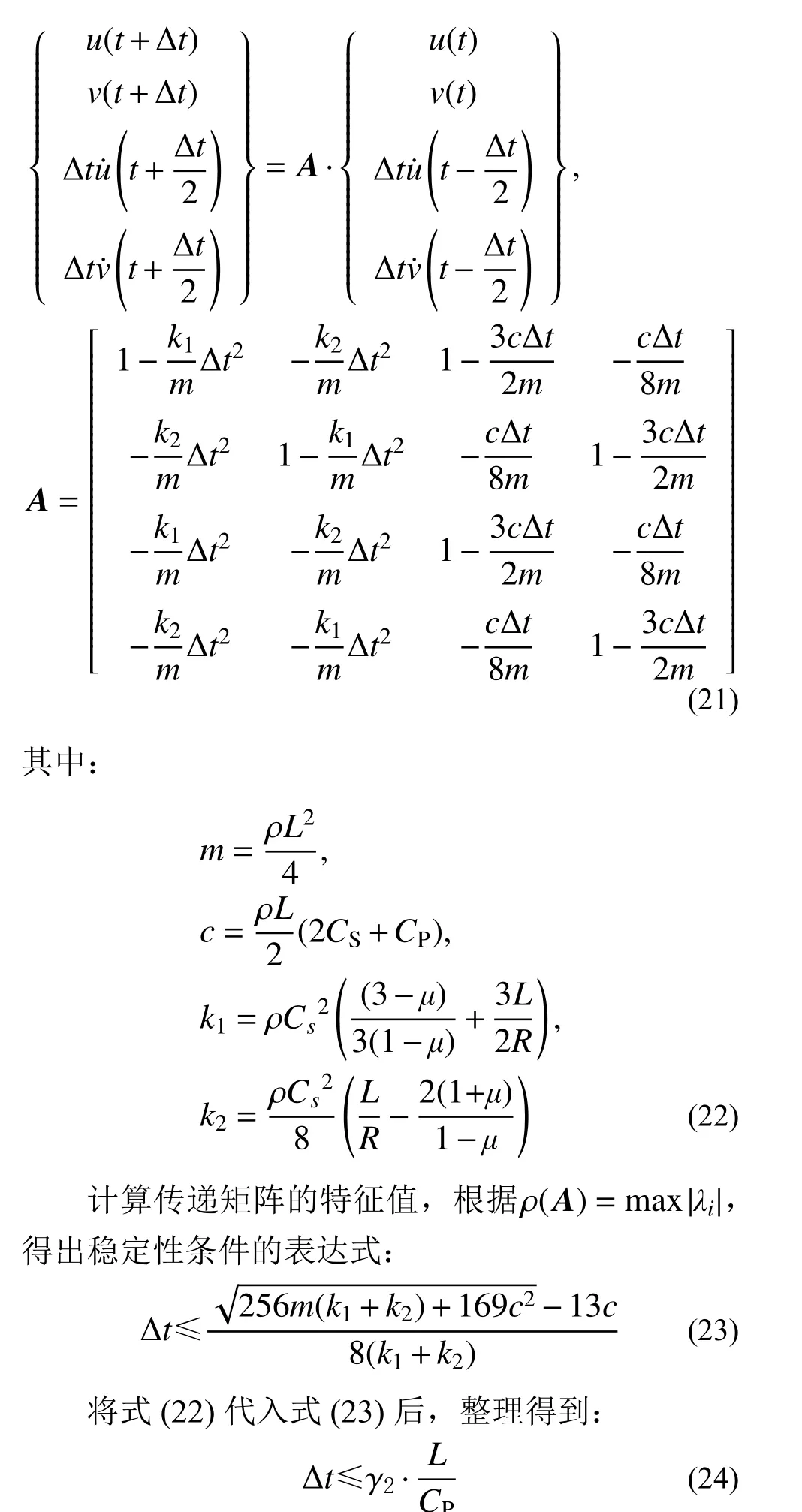
其中：

式(24)即為角點處局部系統穩定性條件的解析表達形式，觀察可知影響角點局部人工邊界子系統穩定性的參數與側邊相同，但各自貢獻不同。

3.3 角點自由邊界子系統穩定性分析

為進一步研究角點處自由邊界子系統的穩定性，如圖10 所示。研究對象為編號為1、2、4、5 的四個節點。子系統中既有單元內部節點，也包含邊界處節點。將四節點正方形平面單元質量、阻尼和剛度矩陣按節點編號組裝后，可得到子系統的剛度、質量和阻尼矩陣，均為8×8 階對稱矩陣。將整體運動方程按照式(14)中心差分格式展開，得到16×16 階傳遞矩陣。該傳遞矩陣無法得出解析形式的穩定性條件，可代入參數計算數值解。考慮穩定性條件受系統截止頻率影響，自由邊界子系統截止頻率要低于固定邊界子系統，由此判斷后者穩定性條件應比前者嚴格，下一節將進行驗證。

4 穩定性條件比較

為比較3 種人工邊界子系統的數值計算穩定條件，采用兩組參數進行分析，具體參數見表1。

表1 兩組參數值(無量綱)Table 1 Two sets of parameter values (dimensionless)

側邊固定和角點固定子系統的穩定條件可由式(19)和式(24)獲得，角點自由邊界子系統的穩定條件可采用數值方法獲得。3 種子系統譜半徑的計算結果見圖11。當譜半徑小于等于1 時，數值計算滿足穩定性條件，由圖11 可以直觀地比較兩組參數條件下3 種子系統的穩定條件。

表2 中對3 種局部子系統和內部系統滿足穩定性條件的臨界時間步長進行了定量比較。內部系統的穩定性條件( ?t=L/CP)未考慮粘彈性人工邊界單元對數值算法的影響，最為寬松；側邊和角點子系統考慮了粘彈性人工邊界單元質量、等效剛度和阻尼對穩定性的影響，穩定性條件要比無人工邊界單元時更為嚴格。四周固定的角點處邊界節點只共享1/4 內部單元質量，其子系統截止頻率最高，因此穩定性條件最為嚴格。以上3 種子系統數值積分穩定條件的對比表明，采用粘彈性人工邊界單元時，系統數值積分的穩定條件由角點區控制。

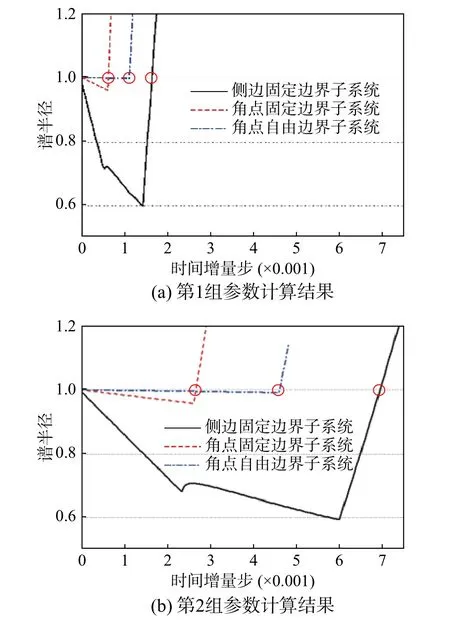
圖11 三種子系統的譜半徑對比Fig. 11 Comparison of spectral radius of three subsystems

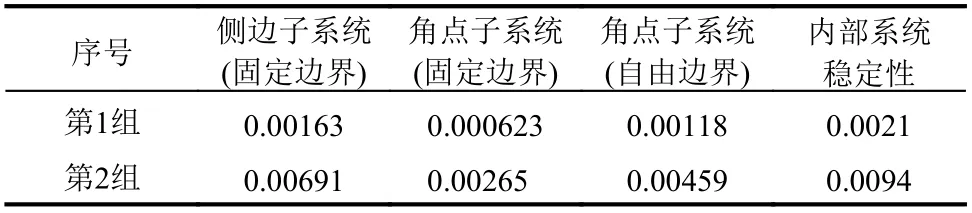
表2 穩定性條件比較(無量綱)Table 2 Comparison of stability conditions (dimensionless)

5 算例驗證

5.1 均勻半空間模型

為驗證以上穩定性分析的準確性，按第一組參數建立有限元近場模型，模型尺寸為320×160，內部介質密度為2500，剪切波速為500，泊松比為0.3，網格尺寸為2×2，模型側邊和底邊最外層單元是粘彈性人工邊界單元，如圖12 所示。采用持時為0.2 的脈沖作為動力荷載，施加于模型中點處，時程曲線如圖13 所示。分別按照內部介質數值穩定條件(?t=0.0021)、側邊子系統穩定條件(?t=0.00163)、固定邊界角點子系統穩定條件(?t=0.00623)，采用固定時間步長的顯示時域逐步積分算法對整體模型進行計算。

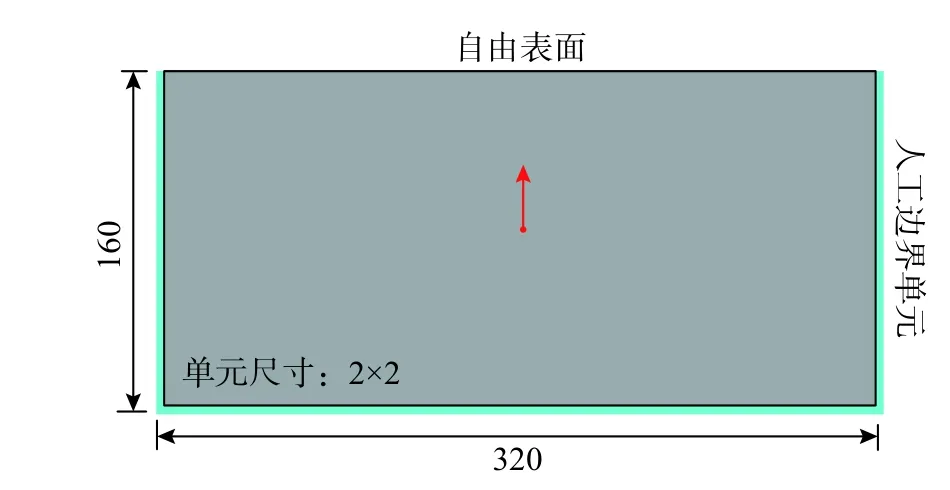
圖12 均勻半空間算例模型圖Fig. 12 Homogeneous half apace example model diagram

圖13 動力荷載時程曲線Fig. 13 Dynamic load time history curve

按照內部介質數值穩定條件(?t=0.0021)計算時，由于不滿足側邊(底邊)子系統穩定條件，因此P 波傳播到距離波源最近的底邊節點時發生失穩，如圖14 所示；按照側邊子系統穩定條件(?t=0.00163)計算時，由于不滿足角點處子系統穩定條件，波動傳播到模型角點處時發生失穩，如圖15所示，其中U為介質中的位移，以上兩種穩定條件均無法完成整體有限元模型的計算。

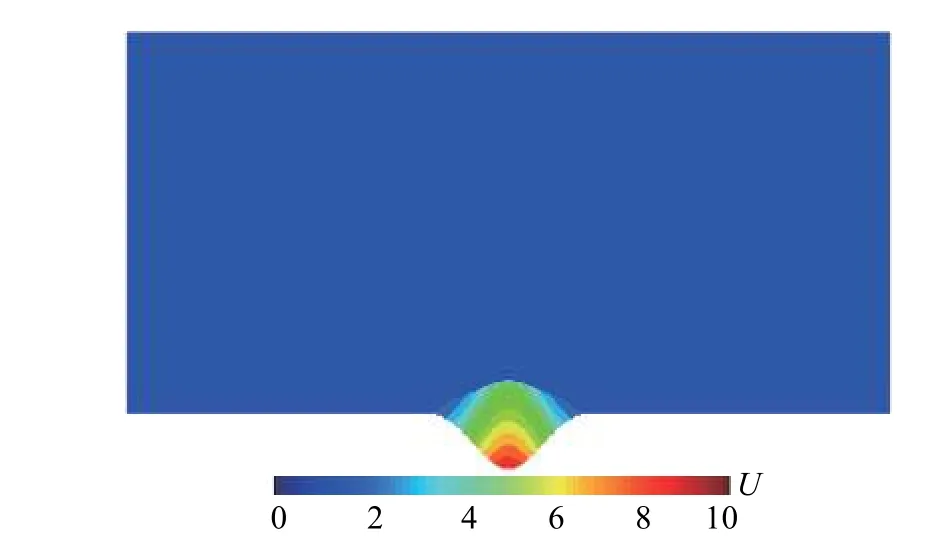
圖14 按內部穩定條件計算時底邊失穩狀態(0.11 時刻)Fig. 14 The unstable state of the bottom edge when calculated according to internal stability conditions (time 0.11)

按照角點處子系統穩定條件(?t=0.000623)計算時，可順利完成整體模型的動力顯式計算，粘彈性人工邊界單元很好模擬了外行波向無窮遠的輻射，結果如圖16 所示。此外，通過進一步的計算分析發現，當整體穩定條件取值略大于角點子系統穩定條件時(例如?t=0.00085)，模型角點處也發生失穩，失穩狀態與圖15 相同。

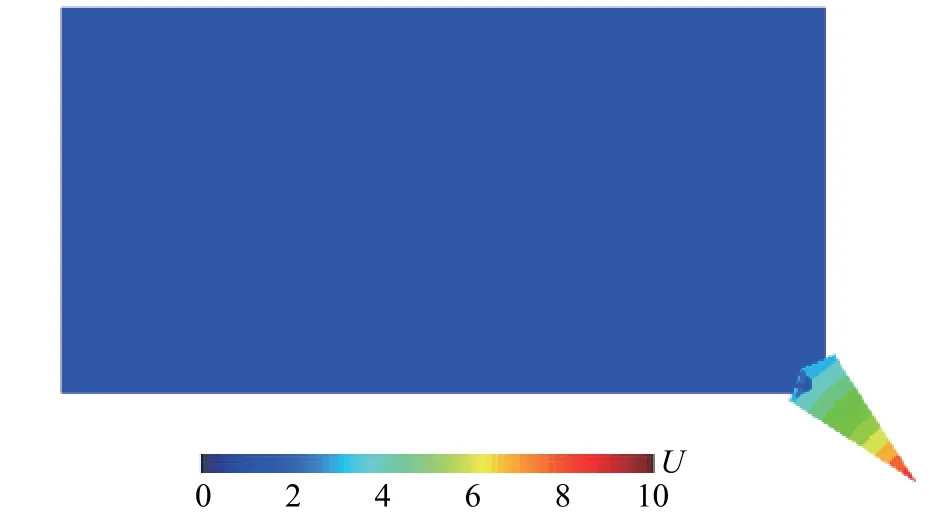
圖15 按側邊子系統穩定條件計算時角點失穩狀態(0.19 時刻)Fig. 15 The unstable state of the bottom edge when calculated according to the stability conditions of side subsystem (time 0.19)

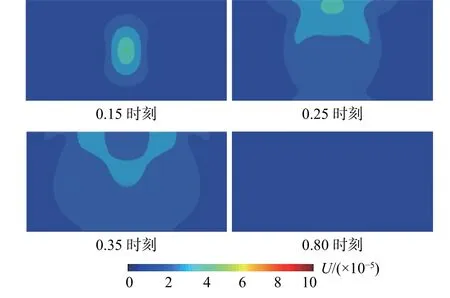
圖16 按角點子系統穩定條件計算結果Fig. 16 Results calculated by the stability conditions of the corner subsystem

以上計算分析驗證了采用粘彈性人工邊界單元時，整體模型顯式數值積分算法的穩定性由角點區域控制，式(24)給出的角點處子系統穩定條件是整體模型數值穩定的充分條件。

5.2 成層半空間模型

為滿足實際場地計算需要，對成層半空間算例進行驗證。成層半空間有限元模型尺寸為320×160，上半部分內部介質密度2000，剪切波速300，泊松比0.27，下半部分內部介質密度為2500，剪切波速為500，泊松比為0.3，整體模型網格尺寸為2×2，模型側邊和底邊最外層單元是粘彈性人工邊界單元，如圖17 所示。脈沖荷載施加于模型中心，如圖13 所示。

表3 給出了成層半空間局部子系統和內部系統滿足穩定性條件的臨界時間步長。模型中的上層介質只有側邊子系統，無角點子系統，下層介質兩者均存在。

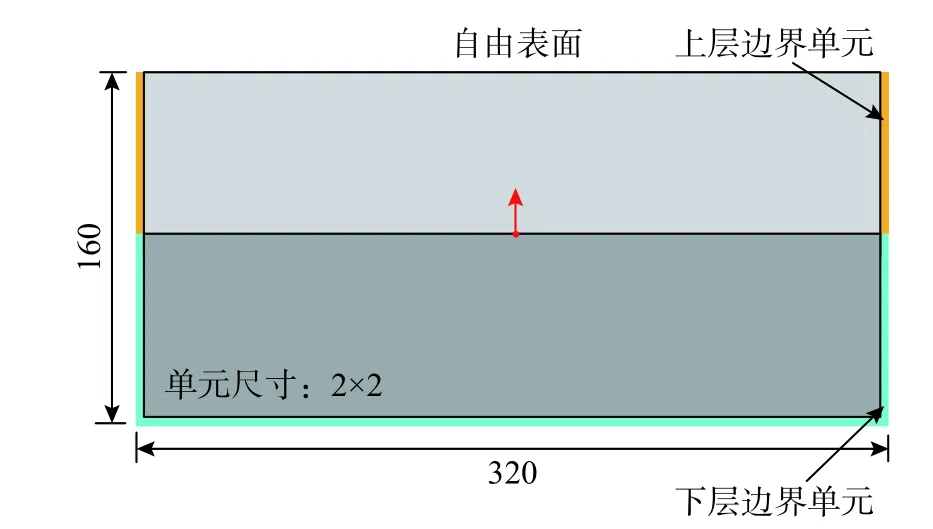
圖17 成層半空間算例模型圖Fig. 17 Layered half space example model diagram

表3 成層半空間穩定性條件比較(無量綱)Table 3 Comparison of stability conditions in layered half space (dimensionless)

經比較發現，上層介質中滿足內部系統穩定條件的時間步長(?t=0.0037)大于側邊子系統穩定時間步長(?t=0.0028)。而二者均比下層介質內部系統穩定的時間步長 (?t=0.0021)要寬松。因此，當采用上層介質穩定性條件對整體模型計算時，首先發生失穩的是下層介質的內部系統，如圖18所示。

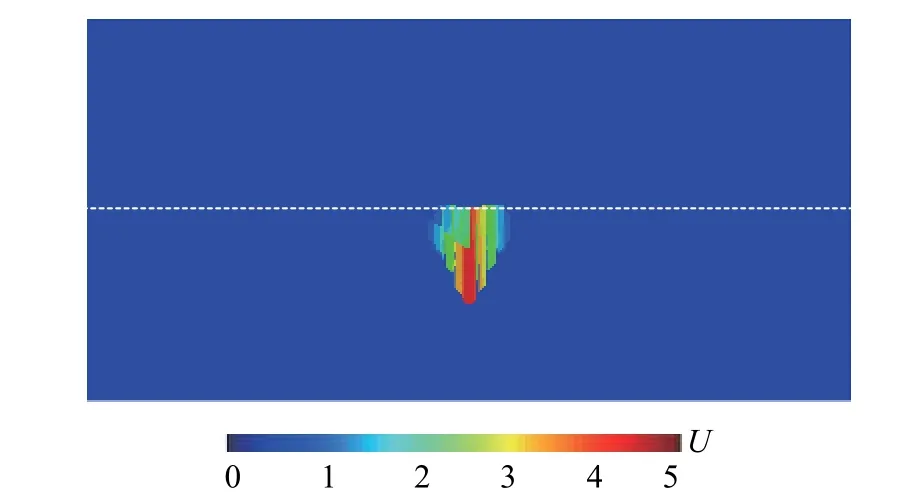
圖18 按上層介質穩定條件計算時下層介質內部系統失穩狀態(0.1 時刻)Fig. 18 The unstable state of the internal system in lower media when calculated according to the stability conditions in upper media (time 0.1)

采用下層介質內部系統穩定條件(?t=0.0021)計算時，整體系統失穩狀態與圖14 相同；采用下層介質側邊子系統穩定條件計算時(?t=0.00163)，失穩狀態和圖15 相同。

按照下層角點子系統穩定條件(?t=0.000623)計算時，可順利完成整體模型的動力顯式計算，分層介質中，粘彈性人工邊界單元也可很好地模擬外行波向無窮遠的輻射，結果如圖19 所示。成層半空間算例進一步驗證了采用粘彈性人工邊界單元時，整體模型顯式數值積分算法的穩定性仍然由角點區域控制。

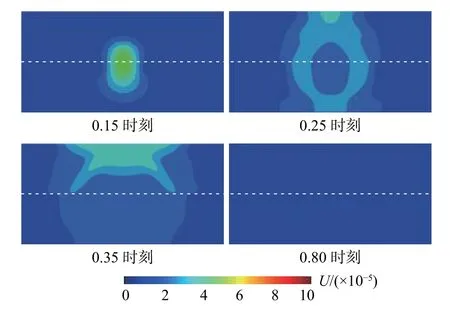
圖19 按下層介質角點子系統穩定條件計算結果Fig. 19 Results calculated by the stability conditions of the corner subsystem in lower media

6 結論與展望

本文將整體模型數值穩定性問題合理轉移到若干局部子系統中，充分考慮粘彈性人工邊界單元和內部單元節點間的運動耦合效應，通過傳遞矩陣譜半徑分析方法推導出各局部子系統顯式時域逐步積分(中心差分)數值穩定條件的解析解和數值解。通過計算軟件驗證理論分析的可靠性。具體結論如下：

(1) 對于大規模數值計算問題，可選取局部的子系統并對其進行顯式時域逐步積分算法的穩定性分析，該穩定性條件與整體系統穩定性條件相同或近似。

(2) 采用粘彈性人工邊界單元時，受人工邊界單元質量、剛度和阻尼影響，整體系統的穩定性條件與內部介質的穩定性條件不同，前者的穩定性條件更為嚴格，需使用更小的積分步長以滿足整體系統的數值穩定。

(3) 采用粘彈性人工邊界單元時，整體模型顯式數值積分算法的穩定性由角點區域控制，本文給出了角點處子系統數值積分的穩定性條件，該穩定性條件是整體模型數值積分穩定的充分條件。此外，本文給出的穩定性條件是以正方形平面單元為對象推導的，同樣適用于矩形平面單元，由于系統穩定條件受最小單元尺寸影響，可使用矩形單元的最小邊長作為參數計算穩定性條件。

下一步展望：

(1) 對于三維粘彈性人工邊界單元，同樣可以利用本文提出的傳遞矩陣譜半徑分析方法對顯式時域逐步積分算法的穩定性條件進行分析，三維問題涉及的局部子結構更為特殊，傳遞矩陣的生成和特征值求解更加復雜，需進一步開展研究。

(2) 相比隱式算法，顯式算法的解耦特性對于求解大范圍復雜工程場地問題更有優勢。本文的研究成果為在顯式算法中合理使用粘彈性人工邊界單元提供了理論依據。可在此基礎上進一步開展分析和研究，以改善使用粘彈性人工邊界單元時顯式算法的穩定性，提高大范圍工程場地問題的計算效率。