色紡紗計算機配色技術的研究現狀及展望

崔翔宇 夏 鑫 楊月茹 張思雨 程 璐

（新疆大學，新疆烏魯木齊，830046）

色紡紗是由多根已著色或具有天然彩色的散纖維，按一定比例混紡而成的紗線。它采用“先著色，后紡紗”的加工工藝，不僅免去了傳統紡織中的染整工序，減少了污染，而且避免了染色時常出現的浸染、沾色等問題；在后整理時，色紡紗亦減少了纖維間因收縮或染整性能相異而形成的疵點［1］。多樣的混紡工藝使得色紡織物的色彩豐富自然，色澤柔和含蓄，風格特異，色紡產品由此深受消費者喜愛，色紡工業的發展在近幾年也相當迅速。

但色紡紗工業依然面臨著很多亟需解決的問題與挑戰，其一便是色紡紗計算機測配色的效率與顏色表達的準確度。本文擬從色紡紗的成色機理出發，綜述并對比近年來諸學者在色紡紗計算機測配色方面的研究進展，對未來研究方向做出預測。

1 色紡紗成色機理

1.1 色紡紗顯色原因

因異色纖維排列足夠緊密，色紡紗交織所成的色點面積與視覺距離之比非常小，而人眼因分辨率的不足，將無法識別各單根有色纖維的色彩，感受到的是有色纖維混和體所呈現的一種新色彩。

這種以空間混合為主的成色機理，與加法混合、減法混合所不同的是，前者并非是色彩的真正混合，而是通過視覺距離與分辨率的關系達成。當人眼或其他感光元件距織物表面有一定距離時，即可呈現色紡織物的混色效果［2］，如圖1所示。

圖1 不同視覺距離下色紡織物的混色效果

1.2 色彩的空間混合

當各種顏色并置于一起，且它們的視網膜投影足夠小時，這些不同的顏色刺激會同時作用到視網膜上非常鄰近部位的感光細胞，以致眼睛很難將它們獨立分辨，從而在視覺上產生色彩混合，這種混合稱空間混合，又稱并置混合［3］。

空間混合成色的效果取決于并置顏色排列的有序性、各顏色的對比度與互補關系、觀察距離等3個方面。

色彩空間混合時，各部分依然保持原色，其混合產生新顏色RGB值可以用式（1）～式（3）表示。

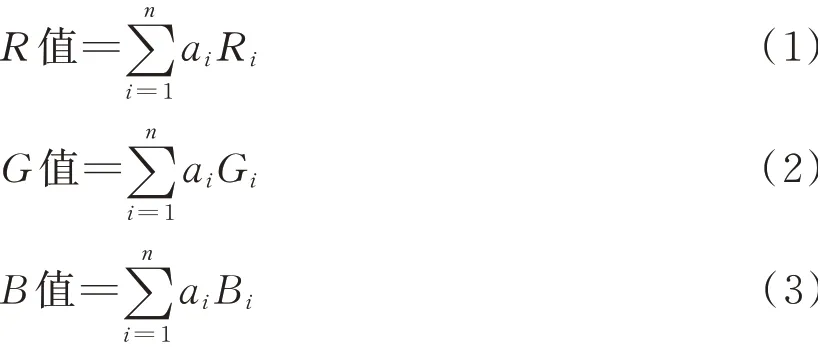
式中：ai表示混和顏色中第i組分所占百分比；Ri、Gi、Bi分別表示第i組單色樣品的RGB值。

2 計算機配色算法

2.1 光譜匹配

反射光譜決定紡織品顏色，使產品的反射光譜與標準樣品相匹配，不受光源和觀察者的影響，可達到最完善配色，又稱無條件匹配。其表達式見式（4），其中：P=WDΦ。

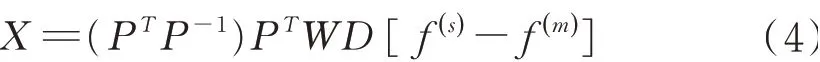
式中：X表示3種單色纖維分別的配比；W為31×31的方陣，其對角線是不同波長對應的權重因子，其余元素為0；D為31×31的方陣，其主對角線上排列標準樣中各不同波長對應dλ值，其余元素為0；Φ在Stearns-Noechel模型與Friele模型中分別為關于標準樣和真實打樣的中間函數，為列矢量。

實際應用中，在400 nm～700 nm之間，每10 nm選取一個數據點以求得對應權重因子，羅列方程進行計算，最多可求出31種單色纖維的混色比。但光譜匹配很難使得實際打樣與標準樣的反射光譜完全匹配，故不斷尋求更為接近的擬合樣。

2.2 三刺激值匹配

三刺激值匹配擬通過真實打樣與標準樣的三刺激值進行比對相等，從而獲得有效配方，其優勢是不要求配色結果在反射光譜上與標準樣相同。

應用了最小二乘法求解的三刺激值匹配可求解3種以內的單色纖維混色比［4］，對多色混色產品的生產有較強的制約性。同時，較光譜匹配的劣勢是，三刺激值匹配過程對光源、觀察者及儀器均有嚴格要求［5］，且易產生同色異譜現象。

但由于光譜配色的計算復雜及成本較高，在實際生產中難以達到經濟且優良的擬合效果，故當下三刺激值匹配更普遍應用于生產。

3 計算機配色的理論模型

3.1 Kubelka-Munk理論

1939年，Kubelka與Munk基 于 完 整 輻 射 理論，提出Kubelka-Munk理論，建立了分光反射率與吸收系數、散射系數之間的函數關系。

在有色織物的計算機配色領域，簡化處理得到式（5）。

式中：ρ∞表示染色試樣無限遠時的反射率；K、S分別表示試樣的吸收系數與散射系數。

該理論推導時建立的假設［6］：樣品界面上折射率必須無變化；光線在介質內必須被足夠地散射，以致呈完全擴散狀態；光線在介質內的運動方向或所謂通道只考慮朝向相反（一個朝上，一個朝下）且垂直于界面的兩個。

3.1.1 Kubelka-Munk單常數理論

纖維與染料對光的吸收系數K與散射系數S可加和，當染料已溶進纖維，即以分子形式存在且含量很小，故擬認為染料對纖維散射的影響是微不足道的，由此可將散射看作是由紡織纖維決定的，K/S值的計算推導見式（6）。

式中：K0、S0分別表示纖維的吸收系數與散射系數；Ki、Si分別表示各染料的吸收系數與散射系數。

Kubelka-Munk單常數理論被證明對基于減色混合的紡織品染色配方的預測效果較佳，但因色紡產品成色的特殊性，早期學者未取得滿意的匹配結果，該方案也被認為不適用于色紡紗產品的測配色。

3.1.2 Kubelka-Munk雙常數理論

有色紡織品的吸收與散射系數由各染料的吸收與散射系數共同決定，則配色時，K和S必須分別計算，見式（7）。

式中：（K/S）m表示混色試樣的K/S值；ci表示第i種纖維占試樣的質量比例；Ki、Si分別表示第i種纖維的吸收系數、散射系數。

以往的研究中，對混色織物中單色纖維的吸收系數K和散射系數S求解的常用方法為最小二乘法和相對值法。前者由WALOWIF E［7］最先提出，利用線性最小二乘回歸算法，大大縮小K、S計算值與觀測值間的差異；BURLONE D A［8］則通過假設一種纖維的相對K、S值，以計算混色織物的K/S值。

徐亞亞等［9-10］對數碼轉杯紗的混色紗進行研究，分別建立了利用以最小二乘法和相對值法求解的Kubelka-Munk雙常數混色模型，并對比了兩者對樣本預測的色差。結果表明：對棉型紗，最小二乘法更適用于預測數碼轉杯紗的三原色混色效果及混色纖維比例；而針對毛型紗，則相對值法的預測精度更高。但兩種方法并無顯著優劣之分，并存在進一步提高精度的可能。

2019年，張婷婷等［11］對環錠數碼紡混色紗測配色進行研究，采用相對值法求解參數，構建模型，并結合全光譜匹配和最小二乘法建立配色算法，平均色差控制在2以內。初步實現對環錠數碼紡混色紗的顏色與配方預測。

3.2 Stearns-Noechel模型

1941年，DUNTLEY S Q［12］提出混色樣品反射率是其組成各單色纖維反射率的質量加權和，見式（8）。

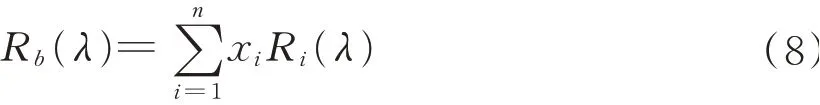
式中：Rb（λ）表示波長為λ時的混色樣品反射率；xi表示第i組單色纖維在混色樣品中所占質量分數，且滿足表示波長為λ時第i組單色纖維的反射率；n表示混色樣中的單色纖維數。

基 于Duntley的 理 論，Stearns與Noechel在1944年建立了Stearns-Noechel模型，修正了由于不同纖維間對光線散射和吸收的互相影響，以及單色反射率與其組成比例間的非線性關系等問題，并驗證其對羊毛混色試樣具有良好預測效果，見式（9）。

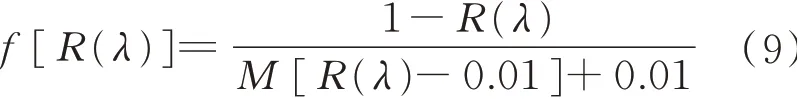
式中：M為可變常量，與混色樣品中單色纖維的顏色、成分及織物組織結構有關；R（λ）表示波長為λ時，混色樣品反射率Rb（λ）或單色纖維反射率Ri（λ）。

Stearns-Noechel模型是色紡紗計算機配色的代表性模型之一，它通過大量試驗不斷修正得出，其中最重要的環節是對可變常量M的確定。目前有較多學者基于該模型，對不同類型織物所對應M值進行研究。以下列舉出諸學者研究得到的幾種常規纖維所對應最優M值，見表1。

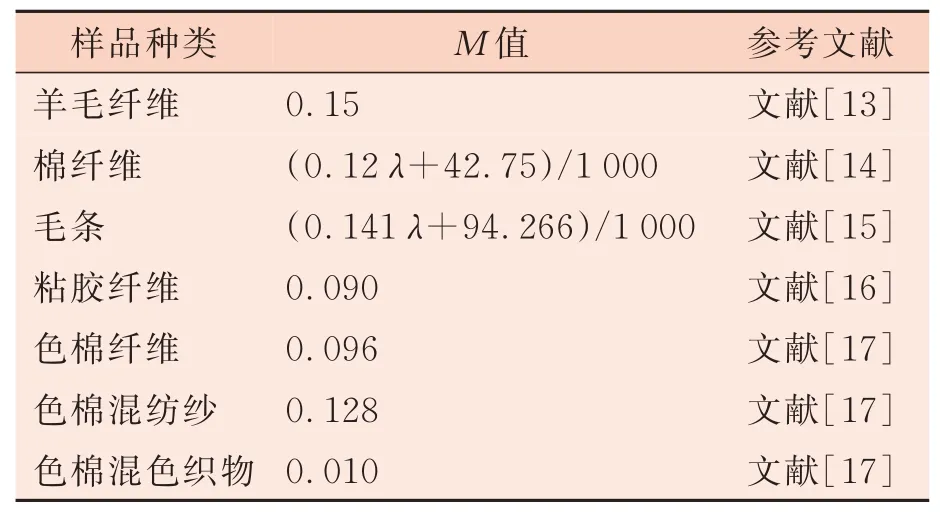
表1 纖維在Stearns-Noechel模型中的參數M值

在過往研究中發現，不同的纖維和織物組織結構，所對應M值不盡相同。針對不同纖維，需通過對大量試樣的配色試驗以優化參數。而生產中，因同種纖維的屬性不同，或紡織工藝與機器設備等因素產生的色差是未知且難以控制的，修色的次數多和困難大直接影響到色紡產品的經濟效益，且對于未公開最優M值的纖維，企業亦不便用作原料，故固定最優M值在實際生產的應用方面仍存在較大局限性。

王玉娟［18］基于Stearns-Noechel模型，建立了完整的計算機輔助色紡紗配色系統，在MATLAB環境中采用M值在［0，1］內賦值迭代的方法，賦予每個混色樣不同的最優參數M值，避免大量前提試驗，而且適用于任何種類纖維及單組份和多組分纖維混和。

2018年，白婧等［19］基于最優參數M值與反射光波長的關系，對Stearns-Noechel模型的參數確定做出優化，分別對非彩色與彩色色紡紗建立M值關于反射光波長的函數，并將配色結果代入CMC色差式驗證，滿足棉纖維配色要求。

2019年，馬崇啟等［20］以Stearns-Noechel模型為基礎，采用賦值迭代法，比對最小色差來獲得最優參數M值預測配方，并在此基礎上將人眼視覺特性（假設人眼對于不同波長的反射率的敏感程度符合正態分布）用于色紡紗配色程序的優化，通過比較標準樣與擬合樣的色差大小判斷配色效果，獲得平均擬合色差為0.201，中位數為0.125，小于0.3，配色效果得到很大提高。

這種建立在擬定算法上，以賦值迭代參數M值尋找最優配色方案的方法，與傳統方案中求固定值相比，更具靈活性與針對性，即依據實際打樣進行針對性配色，減少打樣和修色的復雜工作，且準確度較高，大大提高了配色效率，對企業生產中不同成分混色紗的實際配色更具可行性。

3.3 Friele模型

1952年，FRIELE L F C［21］基 于Duntley理論，根據有色介質對光線吸收和散射特性建立關于反射率R（λ）的函數，見式（10）。

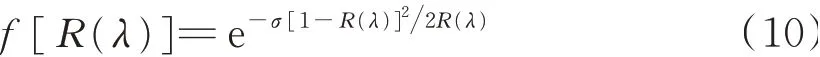
式中：σ為可變常量；R（λ）表示波長為λ時纖維的反射率。

以下列舉諸學者研究所得的幾種常規纖維所對應的最優σ值，見表2。

表2 纖維在Friele模型中的參數σ值

沈加加等基于Friele模型的色紡紗計算機光譜配色原理，對大量試樣求解，優化Friele模型參數σ值，并獲得羊毛色紡紗參數σ值為0.093，棉色紡紗參數σ值為0.128。另外，作者由該試驗指出：色差不是評估色紡紗配色準確性的唯一指標，色紡紗配色中還存在“同色異譜”問題，尚缺乏優良的解決方案。

2017年，馬崇啟等［26］利用MATLAB編寫基于Friele模型的配色算法，對被測單色根據全光譜配色方案求擬合反射率，并在［0，1］范圍內，每間隔0.000 1取σ值進行循環計算，對標準樣和被測樣的反射率進行比對，使得擬合色差小于1時輸出結果。

Friele模型與Stearns-Noechel模型均是基于Duntley的混色質量加權和理論，通過對式中單一可變常量的確定與優化來匹配不同種類色紡紗的配色公式，但前者試驗驗證的纖維種類較少，且較于已有較大成果的Stearns-Noechel模型配色算法，Friele模型在面對相似的參數計算上，并未表現出顯著的更簡便易行或配色更精確等優勢，故針對Stearns-Noechel模型的優化進展更具現實意義。

4 顏色評價與色差控制

4.1 顏色評價基礎

色差是兩試樣在顏色知覺上包含明度差、彩度差、色相差的綜合效應。在CIEXYZ顏色空間中，每種顏色對應互不相同的唯一點，曾有研究發現，在CIE7931x-y色度圖的不同區域，人眼的分辨閾限不同，即人眼的顏色空間是不均勻的，色差也就不能簡單用色點間的距離統一表示。以往學者常基于均勻顏色空間建立相應色差式，擬合了計算結果與視覺間的相關性。常見的色差式列舉如下。

4.2 CIELAB色差式

4.2.1 CIE1976L*a*b*表色系統

CIE1976L*a*b*均勻色彩空間以孟塞爾表色系統為基礎建立，與CIEXYZ顏色空間相比，可更好地依照人眼的色知覺屬性擬合色差，該系統空間結構如圖2所示。其中，L*為明度，C*為飽和度，h*為色相角。

圖2 CIE1976L*a*b*表色系統示意圖

X、Y、Z與L*、a*、b*間可以依據一定的函數關系進行轉換。

4.2.2 CIELAB色差式

色差公式見式（11）。

式中：ΔL*表示明度差；ΔC*表示飽和度差；ΔH*表示色相差。

CIELAB色差式的精確度并不夠好，但其色彩空間因查找顏色方便而被廣泛運用。

4.3 CMC(l:c)色差式

以CIELAB色差式為基礎，由于各影響因子在不同色彩區域內對總色差的貢獻不同，則需根據色彩范圍對ΔL*、ΔC*、ΔH*附相應系數加權求得總色差，其中，CMC（l：c）色差式是現今與視覺相關性較好且運用較為普遍的色差公式，見式（12）。

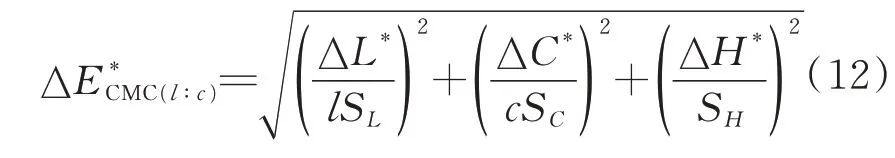
式中：SL、SC、SH分別表示明度差、色相差、彩度差的加權系數，均是與標準樣色彩范圍相關的函數；l、c分別表示調節明度差和彩度差的權重因 子，在 紡 織 行 業 中 取l∶c=2∶1，記 作CMC（2∶1）。

4.4 CIE2000色差式

在與CMC（l：c）色差式相似的CIE94色差式的基礎上修正的CIE2000色差公式，改善了對中性色和藍色區域的預測性能，校正了彩度差與色相差的交互項。其色差評估參數ΔE*00較CIELAB色差式中的評估參數而言，是一個主軸在飽和度方向與人眼辨別臨近區更接近的橢圓［27］，其公式見式（13）。

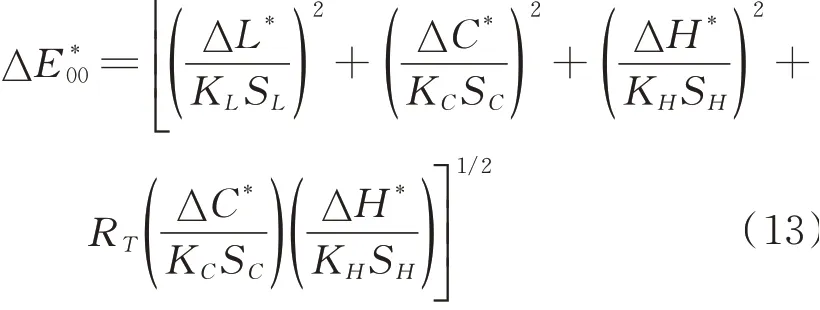
式中：KL、KC、KH分別表示調節明度差、飽和度差、色相差的權重因子；RT表示旋轉系數；在紡織行業中通常取KL=2、KC=1、KH=1。

盡管CIE2000色差式被視為現今最符合人視覺感官的，但其色彩空間依然不是完全均勻的，而在非直接測色獲得顏色值的情況下，運行CIE2000色差式的處理耗時要顯著高于CIE94等［28］。故而，當生產需求偏重于效率時，CIE2000并不一定是最優選擇。

CMC（l：c）色差式與CIE2000色差式在對大量試樣目測結果分析歸納的方法不同，導致了其加權系數確定的不同。在一些試驗過程中，利用以上兩種公式計算得到的擬合色差不盡相同，無法判斷何者更接近真實色差。但對現有色差公式的改進研究仍具有現實意義。

4.5 反射率偏差評價顏色

視網膜皮層理論指出，視覺顏色與表面的光譜反射率函數有密切的關系，而與投射到視網膜上的光譜特性關系不大［29］。基于物體反射率評價織物顏色，可避免由光照和幾何條件對測色產生的誤差。

對色紡紗配色準確性的評估中，亦有學者采用反射率偏差值代替色差作為選擇標準，以確定配方。

2018年，程璐［30］基于Stearns-Noechel模型，將最優M值的選擇標準由色差最小改為擬合樣與標準樣的偏差值最小，在保證與標準樣色差小于1的前提下，配色精度和擬合度得到提高。

2019年，朱寶基［31］同樣采用反射率偏差值作最優參數選擇標準，優化了基于Friele模型的配色算法，同時評價標準由色差改為配方相對偏差。

值得一提的是，在以上研究中均出現了以色差為標準選擇的配方與以反射率偏差為標準選擇的配方間存在較大差異的現象，而該問題尚未得到合理的解釋。

4.6 對色差控制的其他研究

2019年，張靖晶［32］針對計算機配色的基礎問題進行研究，分析了三刺激值計算的誤差原因，分別針對測量間隔和帶寬，測量范圍進行優化，所采用的Table LWL算法使測量誤差減小到未經處理的0.8%，范圍不足時利用外延方法顯著降低截斷誤差，提高了測算精度。

同年，朱寶基對纖維結合體色彩的影響因素做出研究分析，發現不同紡紗工序導致色差的出現，并發現其色度學參數變化呈一定規律性，從而對試樣的色差進行初步預測。同時提出，規范紗線和織物的測色標準，是減少誤差的重要方式。

5 現存問題及發展方向的預測

（1）現有對色紡紗成色機理的研究仍有待改進，可嘗試進一步探究其空間混合的成色機理，對不同纖維、不同表面結構的織物進行試驗驗證，并將其在配色模型及算法的改進上合理運用，可對現有計算機配色方案的改進有所幫助。

（2）三刺激值匹配算法在應用中出現的“同色異譜”現象仍缺乏有效解決方案，光譜匹配算法的準確性有待進一步提高，對計算量的簡化和測色成本的降低也存在實際研究意義。

（3）基于Kubelka-Munk雙常數模型的擬合配方尚有缺陷，可嘗試進一步優化對參數的計算，減小色差；針對Stearns-Noechel模型或Friele模型，應依據實際生產的條件及需要，優化對參數賦值迭代的方法改進配色方案，并對多種纖維進行試驗，驗證其通用性。

（4）現有色差公式與人眼建立的相關性并不強，且對觀測條件具有嚴格要求；基于人眼大數據建立更詳細、更準確的對比關系，將更有利于行業優選出適合的公式；實際打樣與不同色差公式計算的標準樣擬合色差不同，尚沒有確切依據證明哪種結果更接近真實色差。

（5）色差并非評估色紡紗配色準確性的唯一標準，以反射率偏差為選擇標準的算法仍有待進一步研究；對試驗中出現的色差最小的擬合配方與真實反射率偏差最小的擬合配方不一致現象可成為色紡紗計算機配色的重要研究方向。