風電機組參與電網頻率調節的策略研究

張志恒

(國網江蘇省電力有限公司連云港供電分公司， 江蘇 連云港222000)

0 引言

隨著風力發電在我國的應用范圍越來越廣泛,風電不斷地進入到電網中, 風電與電網之間相互影響的范圍、 程度、 方式在不斷深入, 帶來了一系列融合問題, 如電壓劇烈波動、 微機保護誤動作、 頻率振蕩等[1-5]。

目前, 風力發電所引起的系統頻率問題日益為人們所關注。 由于風電機組自身特有的解耦式控制方式, 風力機的機械動能和電網頻率之間沒有直接聯系, 其轉動慣量沒有應用到電網之中, 因此電網頻率的瞬時波動有所增加。 此外, 風電場輸出功率的隨機性和波動性, 使得電力系統需要更多的備用功率, 以滿足電網頻率一次調節的要求, 增加了系統的運行成本[6-7]。

針對風電所引起的電網頻率問題, 國家電網公司《風電場接入電網技術規定》 要求, 風電場具備參與電力系統調頻、 調峰和備用的能力, 能夠實現有功功率的連續平滑調節, 并保證風電場有功控制系統的快速性和可靠性。 現代風力發電機組具備強大的控制優勢, 能夠適時調節自身的各種輸出狀態, 輔助性地解決電網中發生的各種相關問題。

1 風電機組控制策略和功率追蹤模式

1.1 風電機組的控制策略

風力發電機組的控制系統包括對風輪機的控制和對變流器的控制, 其控制框圖如圖1 所示。 轉子側換流器能夠實現對有功功率和無功功率的分別獨立控制, 其有功功率控制是按照風力機控制后給出的功率指令進行, 能夠實現風機轉子轉速的間接控制, 從而使風電機組運行在最佳轉速狀態, 即捕獲最大的風功率。

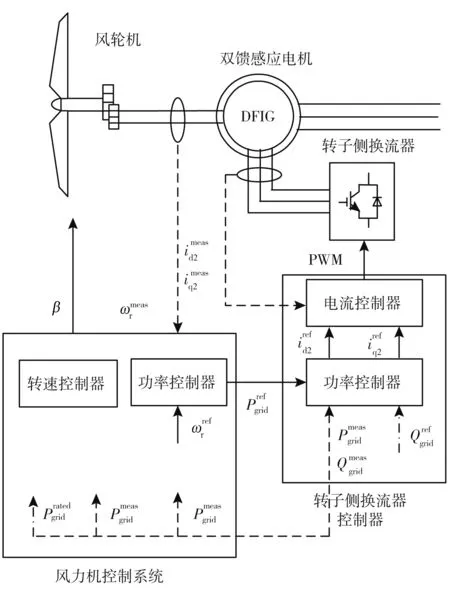
圖1 風電機組的控制框圖(以DFIG 為例)

圖中, 實線表示的是控制后輸出信號, 虛線表示的是測量信號, 點劃線表示的是給定信號； 控制給定信號用上標ref 表示, 控制反饋測量信號用上標meas 來表示。

1.2 風電機組的功率追蹤模式

風輪機的所有運行狀態分為四種模式, 即啟動區、Cp恒定區、 轉速恒定區、 功率恒定區。 一般情況下, 風輪機處于Cp恒定區, 即最大功率追蹤區。 風電機組的參考功率值Pref隨轉子轉速ωr相關的曲線如圖2 所示, 其數學表達式可由公式(1)描述。

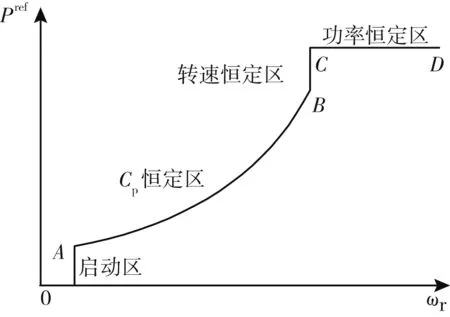
圖2 風電機組的功率追蹤曲線

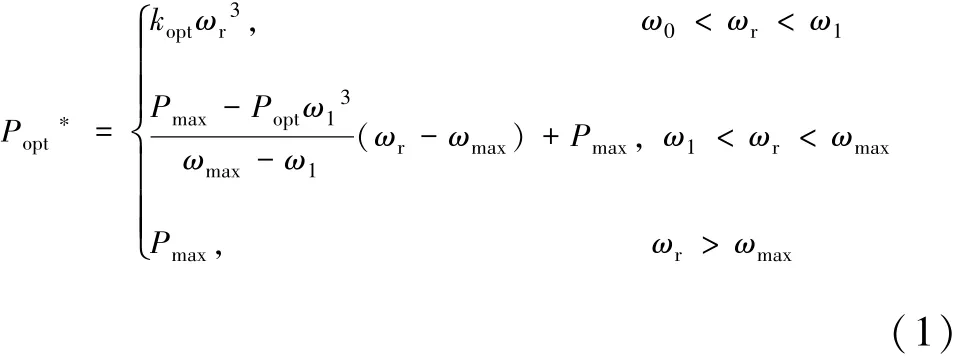
式中,Pmax為風電機組輸出最大有功；ω0為風輪機入網轉速；ω1是在轉速恒定區時的轉速大小；ωmax為風電機的最大轉速；kopt為圖2 中功率追蹤曲線的系數。

2 風電機組參與電網頻率調節的控制策略

風電機組參與電網頻率調節的控制框圖如圖3所示。 其在風電機組原有控制系統的基礎上, 附加了風機的頻率調節模塊[8-12]。 此頻率模塊可根據電網頻率的實際波動狀況進行風電機組的一次調頻或慣性響應控制過程。

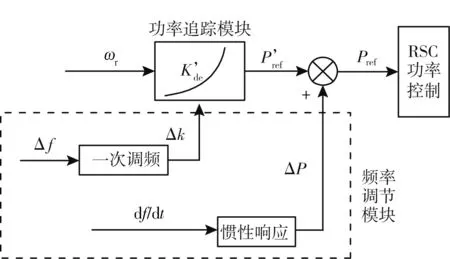
圖3 風電機組參與頻率調節的控制框圖

風電機組進行不同類型頻率響應的判據如下:

式中,Lf、Tf是風電機組進行慣性響應和一次調頻控制的閾值: 當電網的運行頻率偏差較大(如Tf＝0. 05 Hz) 時, 風電機組優先進行一次調頻過程,所形成的變量Δk附加在了功率追蹤環節中, 使得風電機組為電網系統提供更多備用功率； 當系統頻率波動較快(如Lf＝0. 03 Hz/ s) 時, 風電機組可進行瞬時的慣性響應, 風機的輸出參考功率P′ref值立即發生相應變化ΔP, 以減緩電網的能量突變過程。

2.1 風電機組的慣性響應控制

從同步發電機組的慣性特征中可找到風電機組的慣性響應方法。 由同步發電機組可知, 電網頻率波動時機組輸出功率的變化是因為質塊旋轉動能的釋放或吸收, 其數學表達式為:式中,Ek為機組具有的旋轉動能； ΔPs為機組輸出功率的變化量；J為同步機組的轉動慣量；ω為機組轉子的旋轉角速度。

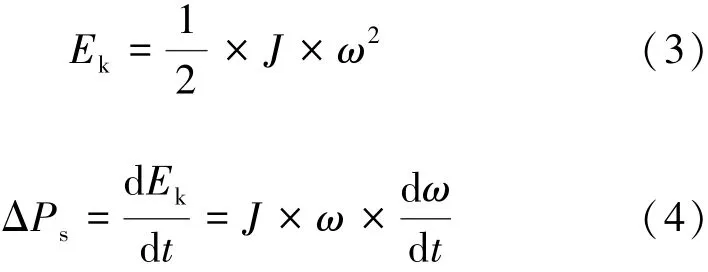
因此, 若要模擬同步發電機組的慣性特征, 風電機組則應該隨系統頻率的變化而改變其最大功率追蹤參考值P′ref的大小, 其變化量ΔP可表達如下:

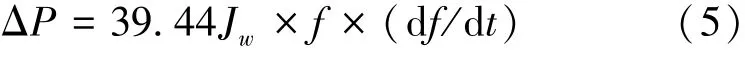
式中,Jw為風電機組的虛擬轉動慣量, 其值為負數； 39. 44Jw為風電機組的慣量系數。 根據以上分析設計的風電機組慣性響應模塊如圖4 所示。

圖4 中設置了死區, 使風電機組僅在系統頻率快速變化時才啟動慣性響應模塊。 此模塊對于系統頻率的變化率按慣量系數(k1＝39. 44Jw) 形成輸出功率的波動量ΔP, 因此頻率變化越快, 風電機組的功率波動就越大。 最后, 功率波動量ΔP與功率追蹤參考值P′ref之和將構成機組新的輸出功率參考值Pref, 從而真正改變風電機組的輸出功率大小。

2.2 風電機組的一次調頻控制

風電機組采用一種超速減載的功率備用法, 具體過程如圖5 所示。 在正常情況下, 風電機組運行于減載功率曲線PT1 上的A 點, 為電網提供一定的備用功率。 當電網頻率發生變化時, 風電機組可以變換至相應的功率曲線PT2 或PT3 上, 在穩定后, 風電機組將運行于B 點或C 點, 從而增加或者減少風電機組的輸出功率, 完成對系統的一次調頻過程。

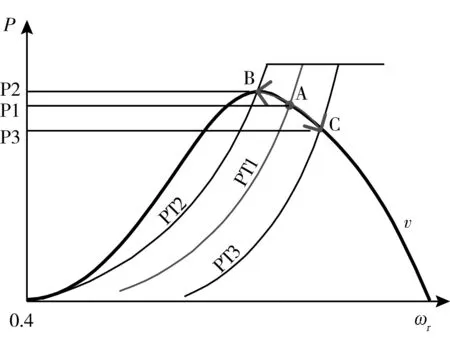
圖5 風電機組的功率備用策略

圖6 是風電機組的一次調頻控制模塊。 其輸入量為電網實測頻率f和額定頻率fref, 對其偏差Δf進行比例調節, 產生Δk的值, 從而形成新的風機功率追蹤曲線k′de, 改變風電機組的輸出功率。 電網負荷增加, 使系統頻率下降能夠增大機組功率曲線系數k′de的值, 提高機組的輸出功率； 電網負荷減少, 使系統頻率升高, 則進行相反的過程。 通常情況下, 風電機組是在kde0＝0. 8kopt的風機功率曲線上穩定運行, 而曲線系數的變化量Δf值被限制在(-0. 2kopt, 0. 2kopt)。 此外, 電網頻率處于(50-Δfmin, 50+Δfmin) 時, 風機將處于一次調頻的死區, 即曲線系數變化量Δk為0。

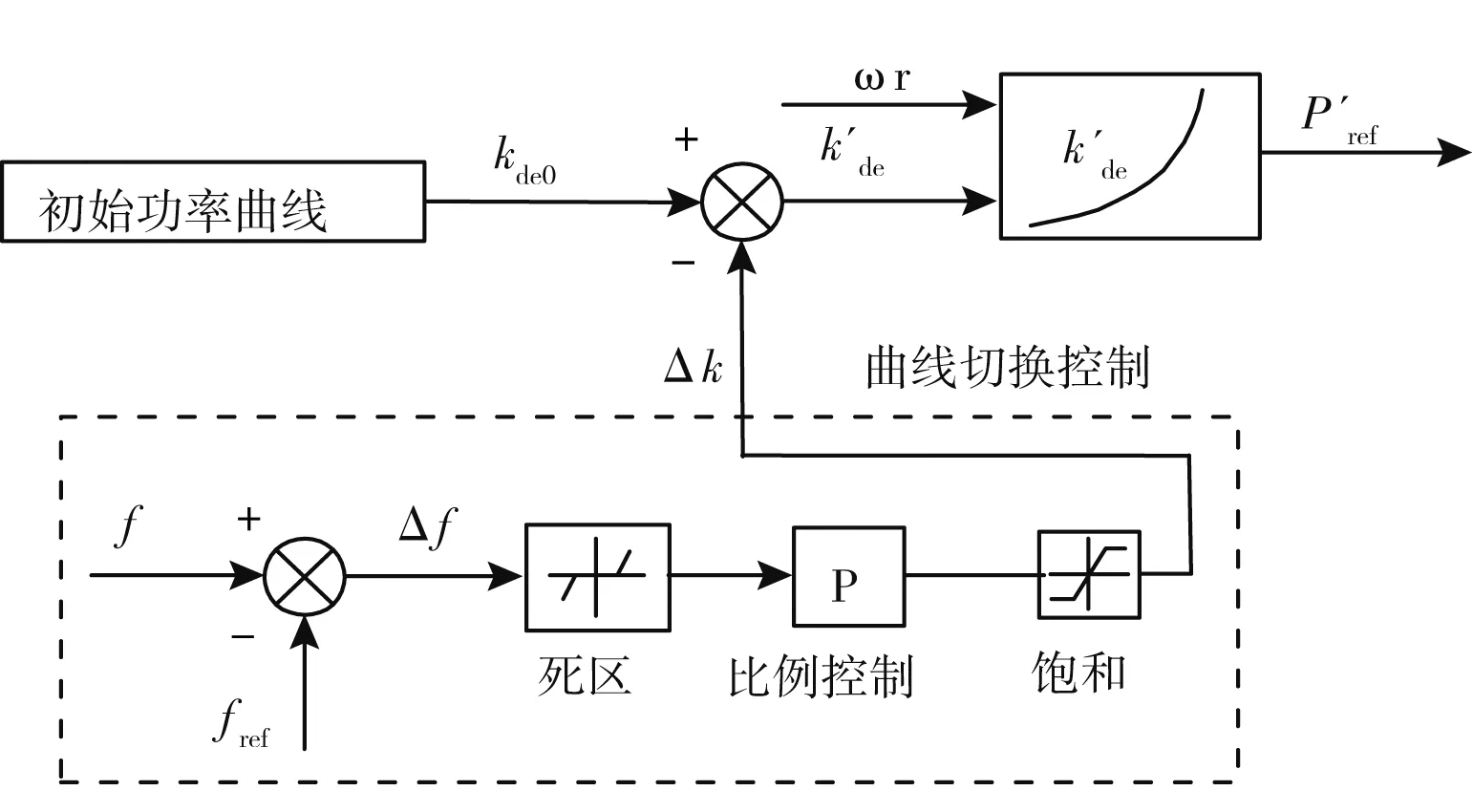
圖6 風電機組的一次調頻模塊

慣性響應與一次調頻控制使風電機組參與了電網頻率的調節, 為系統頻率的控制發揮了風電自身的作用, 從而增強了系統頻率的穩定性。

3 風電機組頻率控制策略的仿真分析

針對一含風電的電網仿真系統, 其結構如圖7 所示, 包含一個風力發電場G3和兩個火力發電廠G1、 G2, 在系統中共有3 處有功負荷(L1、L2和L3), 火力發電廠G1和G2均配有勵磁系統和有功控制系統, 在風電機組的功率控制系統中加入頻率控制模塊, 通過對風電機組慣性和一次調頻的仿真分析, 可驗證風機頻率控制策略的有效性。 此仿真模型中各風電場機組的參數見表1—2。

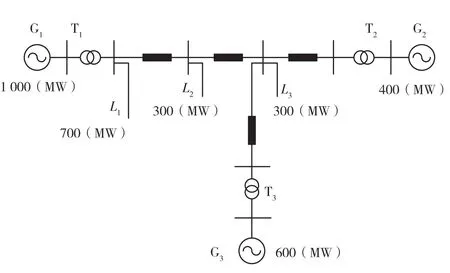
圖7 仿真系統結構

表1 風機參數

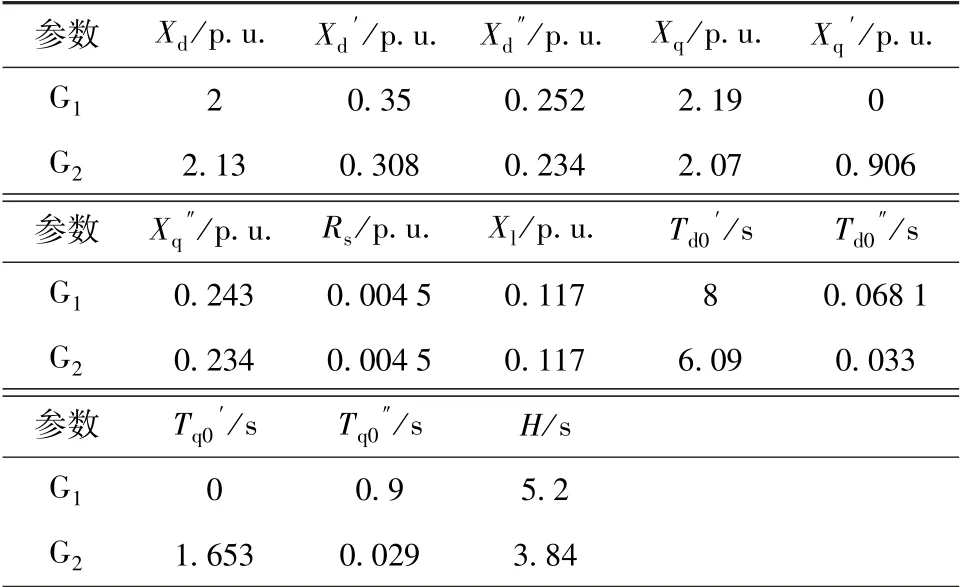
表2 同步發電機G1、 G2 參數

3.1 風機慣性響應過程的仿真分析

初始時風電機組及電網系統處于穩定運行狀態, 風速穩定為7 m/ s。 在3 s 時電網出現500 ms時長40 MW 大小的有功功率投切, 電網頻率和風電機組輸出功率的仿真結果如圖8 所示, 其中虛線表示風機無慣性響應控制策略, 實線表示有慣性響應控制策略時的情況。

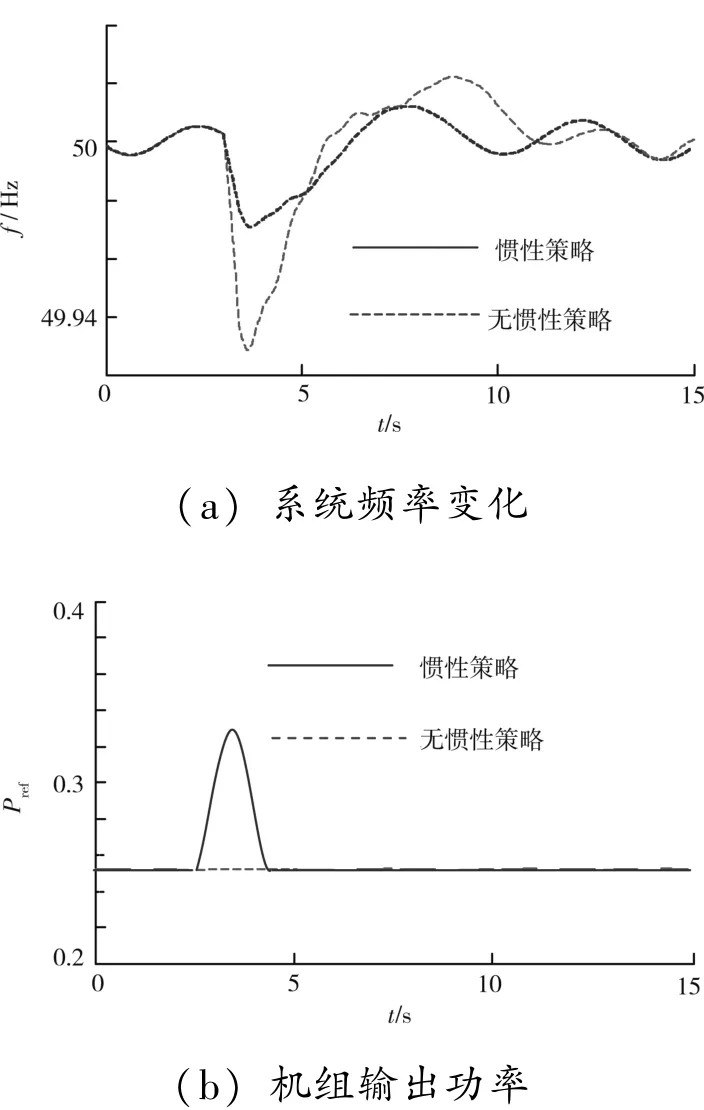
圖8 風電機組的慣性響應

從圖8 可知, 系統頻率的快速下降引發了風電機組的慣性響應控制, 圖8 (b) 的仿真結果說明,在慣性響應的過程中, 風電機組通過風機轉速的快速降低, 其輸出功率會突然增加, 形成了對系統頻率變化的有效慣性響應, 因此頻率的波動比機組沒有慣性控制時有所減緩(圖8 (a) )。

3.2 風機一次調頻過程的仿真分析

初始時風電機組及電力系統處于穩定運行狀態, 風速恒定為7 m/ s。 從3 s 時電力系統開始增加50 MW 負荷并引起電網頻率的下降, 系統頻率和機組輸出功率的仿真結果如圖9 所示, 其中實線表示風電機組有一次調頻控制策略, 虛線表示風電機組無一次調頻控制策略的情況。

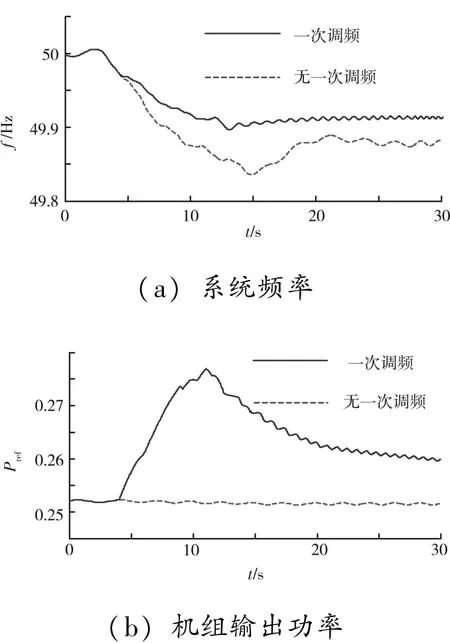
圖9 風電機組的一次調頻

從圖9 可知, 在風電機組參與一次調頻之后,機組的轉速降低, 同時機組的輸出功率增加, 風電機組釋放了備用功率從而減緩了電力系統中的功率不平衡狀況。 由于風電機組的一次調頻控制, 系統頻率與額定值的偏差沒有一次調頻控制時縮小, 因此電網頻率的響應結果有了顯著的改善。

3.3 風機綜合調頻過程的仿真分析

初始時風速恒定為7 m/ s, 風電機組穩定運行于功率追蹤區, 電力系統處于供電-負荷的平衡狀態。 在3 s 時電網開始增加50 MW 的有功負荷, 系統因功率失衡而產生頻率波動, 風電機組參與系統頻率調節的仿真結果如圖10 所示, 其中實線表示有頻率控制策略時效果, 虛線表示無頻率控制策略時效果。

在電網負荷增加時, 系統頻率會首先快速降低, 之后再穩定運行于某一頻率值上。 因為在系統頻率快速下降時, 風電機組進行了慣性支持, 所以電網頻率的初始下降速率將有所減緩。 之后風電機組又根據電網頻率的偏差進行了一次調頻控制, 調整了機組功率追蹤曲線系數, 從而縮小了系統頻率與額定值(50 Hz) 的偏差。 圖10 (a) 顯示在風電機組附加頻率控制模塊后, 電網頻率的響應效果變好, 頻率下降變得緩慢且頻率的穩態偏差變小。總之, 引入本文的頻率控制策略后, 風電機組可根據系統頻率的不同波動情況進行慣性支持、 一次調頻支持, 或者先后進行慣性響應和一次調頻支持, 提供對系統頻率的輔助調節功能, 電網頻率的響應效果變得更好。 因此, 在高風電滲透率地區,風電機組可附加本文的頻率控制模塊。

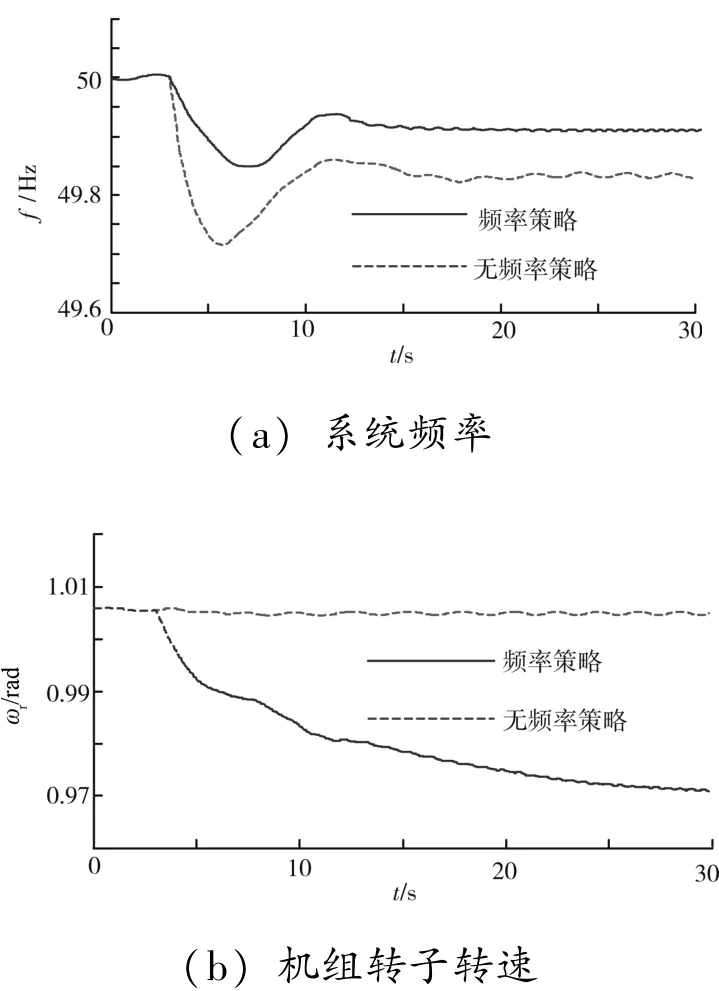
圖10 風電機組的頻率響應結果

4 結論

本文通過慣性控制和一次調頻相結合的方法設計了風電機組的頻率控制策略。 風機慣性響應控制是通過在風電機組輸出功率的參考值上附加慣性變量來完成的, 而一次調頻控制則是通過改變機組的功率曲線從而提供備用功率。 這兩種調頻策略相互補充、 相互協調, 實現風電機組具備與傳統機組相似的頻率響應特性, 從而可以使電網頻率更加穩定。 利用一個電力系統模型的仿真分析, 證明本文所提出的慣性控制與一次調頻結合的調頻控制策略具有有效性, 風力發電機組可對電網頻率提供動態支持, 保證電網的穩定性。