基于“Q值法”的貧困生獎(jiǎng)助學(xué)金分配方法的設(shè)計(jì)

■朱亞彥

（蘇州衛(wèi)生職業(yè)技術(shù)學(xué)院，江蘇 蘇州 215009）

貧困生助學(xué)金主要用于資助家庭經(jīng)濟(jì)困難學(xué)生的生活費(fèi)用開支，從而減輕學(xué)生及其家庭的經(jīng)濟(jì)負(fù)擔(dān)，使得學(xué)生能夠順利地完成學(xué)業(yè)，目前已為世界各國(guó)普遍采用，并成為國(guó)家獎(jiǎng)勵(lì)和資助在校大學(xué)生的主要支撐力量。獎(jiǎng)助學(xué)金的評(píng)定及名額分配涉及到貧困學(xué)生的切身利益，同時(shí)也影響著各二級(jí)院（系、部）之間的團(tuán)結(jié)及整個(gè)學(xué)校的和諧。

一、當(dāng)前高校貧困生助學(xué)金分配的現(xiàn)狀

當(dāng)前，貧困生獎(jiǎng)助學(xué)金的分配存在其特有復(fù)雜性，主要表現(xiàn)如下：

（1）獎(jiǎng)助學(xué)金來源較多。以蘇州衛(wèi)生職業(yè)技術(shù)學(xué)院為例，目前高校的獎(jiǎng)助學(xué)金來源主要有四種，分別是來自于國(guó)家的國(guó)家助學(xué)金、地方政府的殘疾學(xué)生免學(xué)費(fèi)、學(xué)校的關(guān)工委愛心助學(xué)金、社會(huì)的農(nóng)工黨前進(jìn)慈善助學(xué)金等。

（2）獎(jiǎng)助學(xué)金種類多、名額多。以我院2018-2019學(xué)年為例，全年共有11個(gè)主要獎(jiǎng)項(xiàng)2535個(gè)名額分配給了各二級(jí)院（系、部）。

（3）獎(jiǎng)助學(xué)金評(píng)定批次較多，但之間缺少關(guān)聯(lián)性，導(dǎo)致分配不均衡。經(jīng)調(diào)查了解發(fā)現(xiàn)，一學(xué)年中部分同學(xué)獲得多次獎(jiǎng)項(xiàng)，而仍有個(gè)別同學(xué)未獲得過任何獎(jiǎng)助學(xué)金。

（4）獎(jiǎng)助學(xué)金金額各異。譬如：國(guó)家勵(lì)志獎(jiǎng)學(xué)金為5000元/人，國(guó)家助學(xué)金平均為3000元/人，黨員關(guān)愛基金為1000元/人，愛心營(yíng)養(yǎng)餐為400元/人。

（5）參評(píng)各二級(jí)院（系、部）人數(shù)差異較大。以我院2018-2019學(xué)年為例，護(hù)理學(xué)院共有1110貧困生，而酒店管理系只有32名貧困生。

（6）獎(jiǎng)助學(xué)金的評(píng)定要求靈活多樣。獎(jiǎng)助學(xué)金的評(píng)定根據(jù)不同的種類分別有不同的標(biāo)準(zhǔn)，一類是沒有名額限制但要滿足特定條件，譬如建檔立卡的學(xué)生；一類是有名額限制并且要求品學(xué)兼優(yōu)；還有一類是有名額限制但只要求成績(jī)合格即可。

正是由于上述復(fù)雜性，為了實(shí)現(xiàn)貧困生獎(jiǎng)助學(xué)金更加合理、公平的分配，本文提出了一種基于“Q值法”的貧困生獎(jiǎng)助學(xué)金分配方法，能夠更加全面地、系統(tǒng)地解決該問題。

二、“Q值法”評(píng)價(jià)概述

設(shè)共有m方參與名額分配，第i方的人數(shù)為pi,已占有名額數(shù)為ni,i=1,2,3,…,m。當(dāng)總名額增加1個(gè)時(shí)，計(jì)算

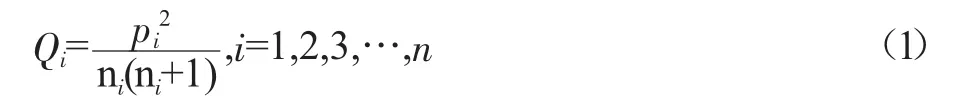
應(yīng)將這一個(gè)名額分給Q值最大的一方，這個(gè)名額分配方法稱為Q值法。

Q值法提出了相對(duì)不公平度這一衡量公平程度的數(shù)量指標(biāo)，較好地考慮到各方的不公平程度，最大限度地保持了公平。但這一方法要求參與分配的各方至少已經(jīng)有了一個(gè)名額，在總名額較少或參加人數(shù)相差較大的情況下也可能存在較大的“不公平”。

三、基于“Q值法”的貧困生獎(jiǎng)助學(xué)金分配方法

解決名額公平分配問題在實(shí)際運(yùn)用過程中需考慮到除了人數(shù)及名額數(shù)之外的其他各類因素，以保證分配結(jié)果的公平性與合理性。貧困生獎(jiǎng)助學(xué)金的分配具有名額與金額這兩個(gè)要素，同時(shí)還需考慮獎(jiǎng)助學(xué)金的評(píng)定要求等其他軟、硬性指標(biāo)。

本文根據(jù)獎(jiǎng)助學(xué)金評(píng)定要求的強(qiáng)弱程度，優(yōu)先考慮分配要求嚴(yán)格的獎(jiǎng)項(xiàng)，再次考慮金額較大、名額較少的獎(jiǎng)項(xiàng)，最后分配僅有一般分配要求的獎(jiǎng)項(xiàng)。具體分配方法如下。

第一階段，分配沒有名額限制但要滿足特定條件的獎(jiǎng)項(xiàng)。

具有滿足特定條件強(qiáng)制分配要求的獎(jiǎng)項(xiàng)按規(guī)定分配給各系部指定的學(xué)生，并計(jì)算出各系部已分配到的助學(xué)金總金額數(shù)（每個(gè)名額獎(jiǎng)助學(xué)金金額×名額數(shù)）。定義ai(i=1,2,3,…,n)表示第i個(gè)系部該階段分配到的金額總數(shù),則第一階段結(jié)束后，每個(gè)系部獲得的總金額數(shù)所構(gòu)成的集合為{a1,a2,…,an}。

第二階段，分配金額數(shù)較大、名額較少的獎(jiǎng)項(xiàng)。

譬如國(guó)家勵(lì)志獎(jiǎng)學(xué)金，該獎(jiǎng)項(xiàng)名額較少并且要求學(xué)生品學(xué)兼優(yōu)，先根據(jù)獎(jiǎng)項(xiàng)評(píng)定要求，各系部自行篩選，將不滿足基本條件的貧困生去掉，剩余符合要求的貧困生基數(shù)就會(huì)相對(duì)變小好多，同時(shí)各系部之間的參評(píng)人數(shù)差異也會(huì)縮小，從而降低了之前參評(píng)人數(shù)差異較大導(dǎo)致的“不公平”。

接下來先按照比例計(jì)算結(jié)果將整數(shù)部分的名額分配給各系部，然后再用“Q值法”分配剩下的名額，運(yùn)用“Q值法”的公式（1）計(jì)算下一個(gè)名額分配的Q值，Q值最高的系部分得該名額，依此進(jìn)行，直至最后一個(gè)名額分配完畢。同時(shí)，計(jì)算出各系部分配到該類獎(jiǎng)項(xiàng)的金額總數(shù)，定義bi(i=1,2,3,…,n)表示第i個(gè)系部該階段分配到的總金額數(shù)。則第二階段結(jié)束后，每個(gè)系部獲得的總金額總數(shù)所構(gòu)成的集合為{a1+b1,a2+b2,…,an+bn}。

第三階段，分配僅有一般分配要求的獎(jiǎng)項(xiàng)。

該類獎(jiǎng)項(xiàng)的特點(diǎn)是名額較多，評(píng)定要求偏弱，每個(gè)名額所占金額較少，譬如學(xué)院的愛心助學(xué)金。該類獎(jiǎng)項(xiàng)在分配過程中要考慮填平前兩階段獎(jiǎng)項(xiàng)分配后所造成的“不公平”現(xiàn)象。

其中，pi（i=1,2,3,…,n）為第i個(gè)系部的貧困生人數(shù)，ci（=ai+bi）（i=1,2,3,…,n）為該系部已經(jīng)分配到的獎(jiǎng)助學(xué)金總金額，m為當(dāng)前待分配獎(jiǎng)項(xiàng)的金額。

接下來，按照公式（2）計(jì)算當(dāng)前獎(jiǎng)項(xiàng)的每個(gè)待分配名額（金額）的Q值，將名額（金額）分配給Q最大的系部。如果此時(shí)還有系部未獲得任何獎(jiǎng)項(xiàng)，即還未獲得“分配資格”，則優(yōu)先將獎(jiǎng)項(xiàng)名額（金額）分配給該系部，然后再重復(fù)公式（2）的計(jì)算及名額（金額）分配，直至所有名額（金額）分配完畢。定義di(i=1,2,3,…,n)表示第i個(gè)系部該階段分配到的總金額數(shù)，則所有獎(jiǎng)項(xiàng)名額分配完畢后各系部獲得的總金額數(shù)所構(gòu)成的集合為{a1+b1+d1,a2+b2+d2,…,an+bn+dn}。

以上整個(gè)過程就是基于“Q值法”的貧困生獎(jiǎng)助學(xué)金分配方法。

四、應(yīng)用及結(jié)果分析

本文以學(xué)院2018-2019學(xué)年學(xué)生資助管理中心分發(fā)的貧困生獎(jiǎng)助學(xué)金為參考，刪除部分零碎的獎(jiǎng)項(xiàng)，選取名額及金額較多的11個(gè)獎(jiǎng)項(xiàng)進(jìn)行分析。將這些獎(jiǎng)助學(xué)金用基于“Q值法”的分配方法進(jìn)行模擬重新分配，再與傳統(tǒng)按比例分配方案的結(jié)果進(jìn)行比較，數(shù)據(jù)如附表1所示。

對(duì)于傳統(tǒng)按比例分配的方案，通過查看院系部人數(shù)發(fā)現(xiàn)，貧困生人數(shù)最少的院系部人均名額是最高的，貧困生人數(shù)最多的院系部人均名額反而最少。另外，從獎(jiǎng)助學(xué)金金額分配情況來看，這種不均衡性顯得更加明顯，最高人均金額超出平均數(shù)近兩成，同時(shí)人均金額方差的數(shù)值偏高，這也說明了傳統(tǒng)按比例分配方案存在較大的不公平。

對(duì)于“Q值法”分配方案，通過附表的數(shù)據(jù)對(duì)比可以看出，該方案的最終結(jié)果縮小了各院系部之間人均名額分配的差距，使得分配結(jié)果更加合理。同時(shí)，最關(guān)鍵的在獎(jiǎng)助學(xué)金金額分配方面很好地解決了公平分配的問題，最高與最低人均金額差異比較小，基本實(shí)現(xiàn)了獎(jiǎng)助學(xué)金的平均分配。

因此，本文介紹的“Q值法”分配方案要優(yōu)于傳統(tǒng)按比例分配方案。

基于“Q值法”的貧困生獎(jiǎng)助學(xué)金分配方法，將原來復(fù)雜的名額分配問題按照獎(jiǎng)項(xiàng)的評(píng)定要求分解到不同的階段來處理，更加明確了操作流程。同時(shí)，本文還選用更加適宜的數(shù)學(xué)公式來量化分配過程，既考慮名額公平更注重金額公平，使得最終的方案更加科學(xué)、合理。

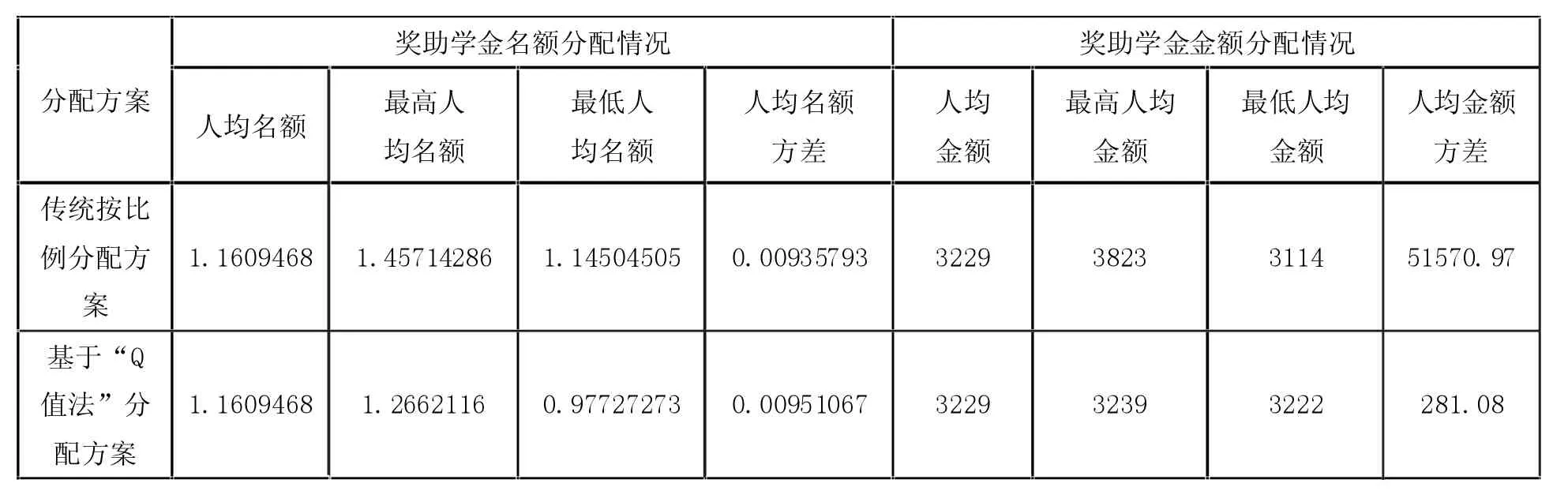
附表1 獎(jiǎng)助學(xué)金名額和金額分配情況