一種基于混沌系統的ZUC動態S盒構造及應用方案

韓妍妍 何彥茹 劉培鶴 張 鐸 王志強,2 何文才

1(北京電子科技學院 北京 100070) 2(國家信息中心 北京 100070)

ZUC密碼算法[1]，又稱祖沖之密碼算法，是一個面向字設計的同步序列密碼算法，已在2011年被正式批準成為3GPP LTE國際標準密碼算法.該算法在設計時充分考慮了軟硬件的可實現性，具有較低的復雜度，是一種應用較為廣泛的輕量級密碼算法.算法的結構主要包含3個基本組成部分，分別是上層線性反饋移位寄存器LFSR、中間層比特重組BR，以及下層非線性函數F.其中，非線性函數F這部分主要依靠唯一的非線性部件S盒來擾亂LFSR層輸出的序列，進而增強算法的安全性.ZUC算法中的S盒是由4個8×8的非線性置換S盒共同構成，即S=(S0,S1,S2,S3).其中S0和S2相同，S1和S3相同.由此可見，ZUC算法中所使用的S盒均是固定不變且未進行復雜混亂過程.因此，設計具有良好性能的S盒是提升ZUC算法性能的一個重要因素.

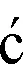
然而，這些基于混沌思想所構造S盒的方法，通常在非線性度、DP和LP等性能方面與傳統的數學構造方法有一定差距.與此同時，上述設計S盒方案雖然能夠滿足基本的置亂特性，但效果并不理想，且由于方案設計的開銷大，造成硬件的可實現性較差.本文基于這些特點提出了復合混沌系統的思想，選取混沌特性良好的Tent和Henon兩個混沌映射進行疊加，同時將圖像置亂的思想引入到S盒的設計中來，利用Arnold映射對復合混沌系統所產生的S盒進行二次置亂，大幅度提高了S盒的非線性度.此外，通過對初始值和控制參數的控制和改變，可以動態地生成不同的S盒.最后，選取一些本文構造的S盒進行DP和LP的性能測試和分析，并與其他設計方法進行對比.此外，將本文利用混沌系統所產生的動態S盒用于替換ZUC算法中固定的S盒，并對其進行軟硬件實現的性能測試，實驗結果表明:本文構造方案所得S盒密碼學特性良好，在增強ZUC算法密鑰序列的隨機性的同時，也兼具較好的軟硬件可實現性.

1 相關描述

1.1 ZUC算法的S盒設計

S盒是ZUC算法中非線性函數F層的重要部分，也是算法中唯一的非線性部件.ZUC序列密碼算法的S盒設計本著高非線性度、低差分均勻性、硬件實現開銷低等原則，共包含4個非線性置換S盒，分別是S0,S1,S2,S3.其中，S0與S2相同，S1與S3相同.S0和S2采用3個4輸入的置換表，結合異或和移位操作進行構造.S1和S3是由一個簡單仿射變換算法和另一個求復雜有限域GF(28)上的乘法逆元算法構成.S0和S1的定義分別如圖1、圖2所示.

若將S0(或S1)的8比特輸入設為x，并用x表示2個16進制數的連接，即x=h‖l，那么S0(或S1)的輸出S0(x)(或S1(x))則為圖1(或圖2)中第h行和第l列交叉的元素.

設S盒的32比特輸入X和32比特輸出Y:

X=x0‖x1‖x2‖x3,

(1)

Y=y0‖y1‖y2‖y3,

(2)

其中,xi和yi均為8比特字節，i=0,1,2,3.則有yi=Si(xi)，i=0,1,2,3.

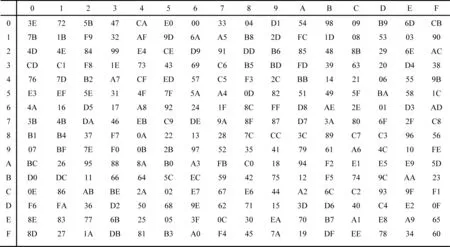
Fig. 1 S0-box圖1 S0盒

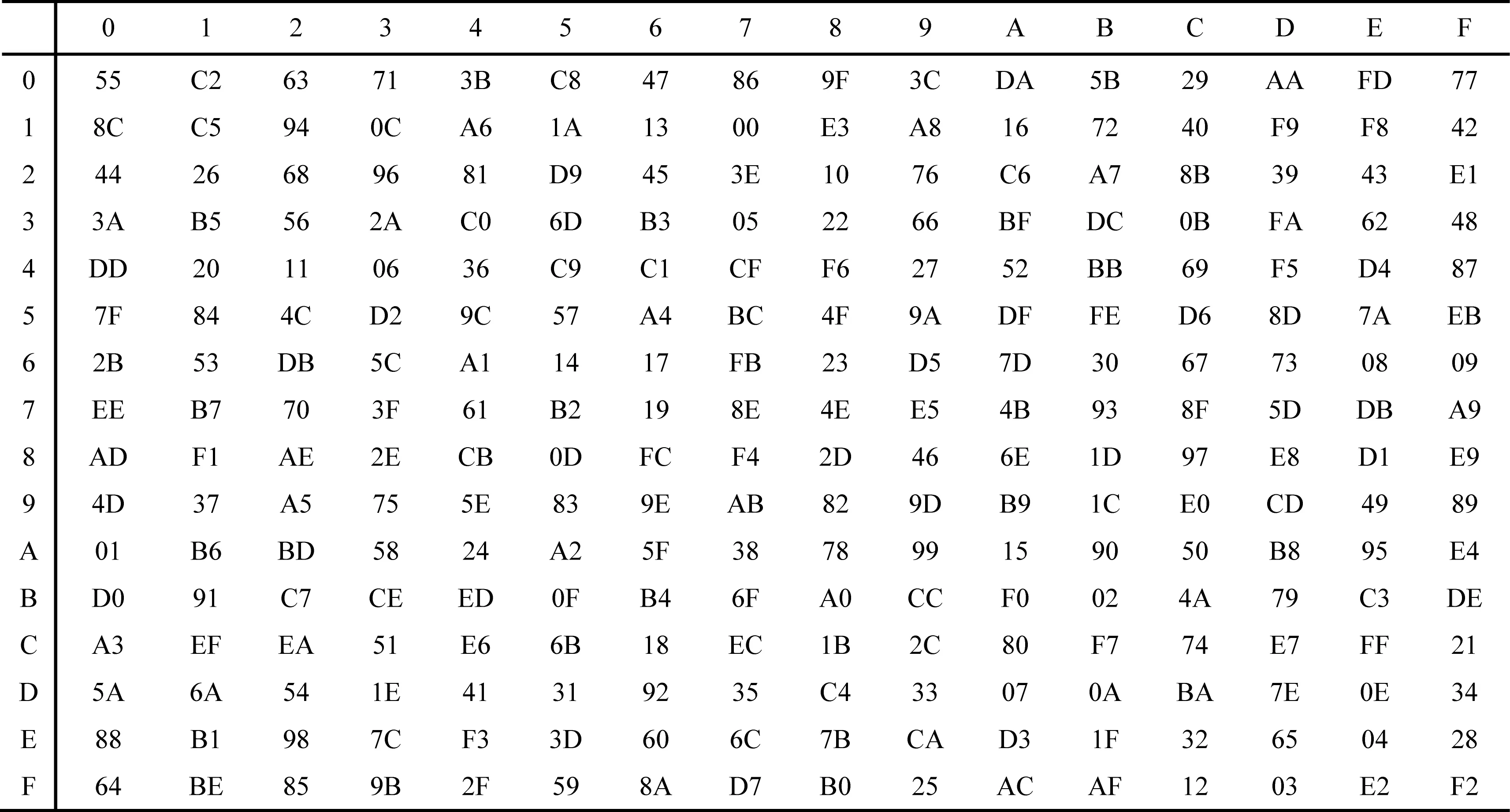
Fig. 2 S1-box圖2 S1盒

1.2 S盒及其設計準則

S盒又被稱為置換盒，本質上可以看作是一張映射表，它是很多密碼算法設計過程中唯一的非線性部件.因此，可以說在一定程度上一個密碼算法的安全性強弱與S盒本身的設計息息相關.S盒的映射一般表示為

S(x)=(f(x1),f(x2),…,f(xm)):
GF(2n)→GF(2m),

(3)

也常表示為S:{0,1}n→{0,1}m，它是將n位輸入映射到m位輸出的非線性過程.目前普遍研究和使用的是8×8 S盒.經過眾多專家和學者對S盒的大量設計和研究，提出了6個用于衡量S盒是否具有優異密碼學性能的測試指標.下面分別詳細介紹這6個重要檢驗指標.

1.2.1 雙射特性

S盒在用于置換時，通常要求其滿足雙射特性，即S盒必須可逆.文獻[15]提供了判斷S盒是否滿足雙射特性的檢驗方法.當m=n時，S盒需滿足的充要條件是：所有分量布爾函數fi的線性運算之和為2n-1.

1.2.2 非線性度

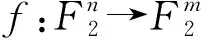
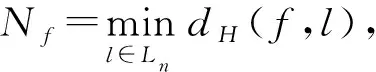
(4)

其中,Ln表示全部n元線性和仿射函數集合；dH(f,l)表示f和l的漢明距離.

1.2.3 嚴格雪崩準則(SAC)

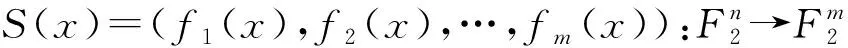
在實際使用時，S盒的嚴格雪崩準則(strict avalanche criterion, SAC)是按照依賴矩陣[18]方式來計算.其中，矩陣中理想值為0.5，如果所有的值都與該理想值接近，則認為這個S盒完全符合嚴格雪崩準則.

1.2.4 輸出間比特獨立性(BIC)

定義3[19].對S盒的2個輸出比特fj和fk(j≠k)，如果fj⊕fk具有很高的非線性，同時符合嚴格雪崩準則的相關要求，則可以保證一個輸入比特對進行取反操作時，對應的輸出比特對相關系數趨近于0.因此，測試S盒的比特獨立性(bit inde-pendence criterion, BIC)性能時，可以對fj⊕fk的非線性度進行計算并判斷其對SAC的滿足程度.

1.2.5 差分均勻性

差分均勻性[20]是判斷S盒在密碼算法中抗差分能力強弱的重要指標.在實際計算時，輸入和輸出之間的異或分布情況通常用差分逼近概率DPf表示：

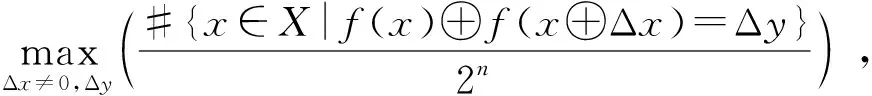
(5)

其中,X表示所有可能輸入的集合，2n是該集合的元素個數，#表示計數，DPf表示輸入改變量Δx時輸出改變量Δy的最大可能性.

1.2.6 線性逼近概率

定義4[21].線性逼近概率LPf.

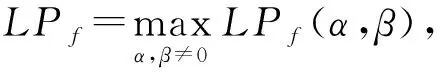
(6)

LPf(α,β)=(2p-1)2,

(7)

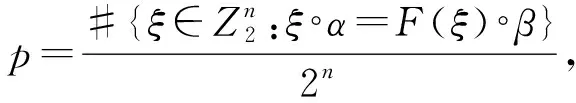
(8)

其中,ξ°α=ξ1α1⊕ξ2α2⊕…⊕ξnαn，#表示計數.

1.3 2種經典混沌系統

眾所周知，混沌系統一般都具有顯著的偽隨機性和高度的初值敏感性，能夠起到增強置亂的作用，特別適合用在S盒設計中.Tent映射和Henon映射是代表性較強的2種混沌系統，本文對這2種經典系統進行迭代，形成新的復合混沌系統.

1) Tent映射系統[22]是一種經典的離散混沌映射系統，目前，利用Tent映射產生的混沌序列在構造混沌加密系統及實現混沌算法等領域中有著非常廣泛的應用.Tent系統映射方程為

(9)

當變量xn∈(0,1)，且q∈(0,1)時，系統處于混沌狀態.

2) Henon映射系統[23]是1976年由Henon提出的一個二維離散混沌系統，其映射方程為

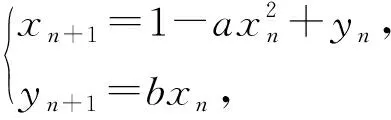
(10)

其中，當系統參數1.07≤a≤1.4，b=0.3時，系統處于混沌狀態.且當變量xn∈(-1.5,1.5)時，取a=1.4，該系統復雜度最大.

2 S盒構造方法

2.1 基于復合混沌系統的S盒設計

本文提出一種基于復合混沌系統的動態S盒構造方案.通過對Tent和Henon兩個混沌映射進行復合，結合混沌映射的迭代，生成一個具有良好性能的8×8 S盒.該方法的具體設計步驟為：

2) 取初值x0，經過式(9)迭代一次得到x1，則第1個小區間上的點表示為x1×l+0×l；迭代n次得到xn，第n個小區間上的點表示為xn×l+(n-1)×l，最終得到n維序列X.

3) 選取2)中得到的序列X為Henon映射的初值，其中令Henon映射中每次x和y的值保持一致，且均來自于序列X，然后經過式(10)進行N次迭代，取所有的y值構成第2個序列Y1.

4)Y1序列中的每個元素分別屬于1～m區間中的一個，依次將元素所在的區間序號記為i，Y2=i(mod 256).

5) 在Y2序列中按先后順序選取256個不相同的元素構成新序列Y，Y序列即為所求的S盒.

上述設計中，Tent映射中q=0.5時，系統呈現短周期狀態，因此q值應避免選擇0.5.此外，在應用時也應避免選取和q值相同的初值，以防止系統演化為周期系統.改變參數q的取值，不僅能夠實現動態產生S盒，而且可以增強混亂效果.上述步驟只涉及簡單的排序和取余操作，可以有效減少算法運行過程的消耗，有助于提升運行速度和效率.最后對生成S盒的DP,LP值進行統計和分析，篩選出具有較好的密碼學特性的S盒，否則對初值進行改變，重復以上5個步驟繼續生成符合要求的S盒.

本文在實際S盒生成的過程中，式(9)中Tent系統參數選取q=0.4，式(10)中Henon系統參數選取a=1.4，b=0.3.當迭代次數n=5 838，N=5 000，初始值x0=0.3時，獲得的混沌系統生成的S盒密碼性能較為良好，如圖3所示，其中DP=0.046 875 0，LP=0.132 813.

2.2 S盒重構

本文結合圖像加密中使用的置亂方法，重構上述復合混沌系統構造方法得到8×8 S盒.在混沌系統產生8×8 S盒后，引入Arnold映射對其進行置亂，將其中數據的位置進行打亂重排，從而實現二次置亂.Arnold映射是一種具有周期性的映射，常應用于混沌序列的置亂過程，可表示為

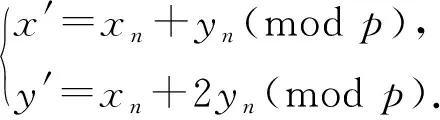
(11)

為了便于應用，通常把它寫成矩陣形式：

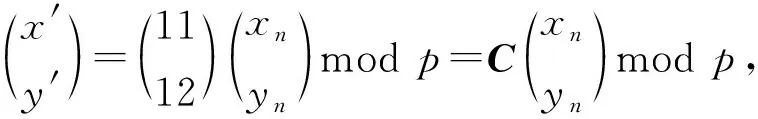
(12)

其中，S盒的行數和列數用n表示，且p=16.若數據在原始S盒中的位置坐標為(x,y)，則經過Arnold映射置亂后的新位置坐標變為(x′,y′).

將上述密碼學性能最好的S盒進行重構后得到新的S盒如圖4所示，其中DP=0.0390625，LP=0.109 375.由此可見，經過Arnold映射二次置亂后的結果與置亂之前相比，提升了的S盒性能.

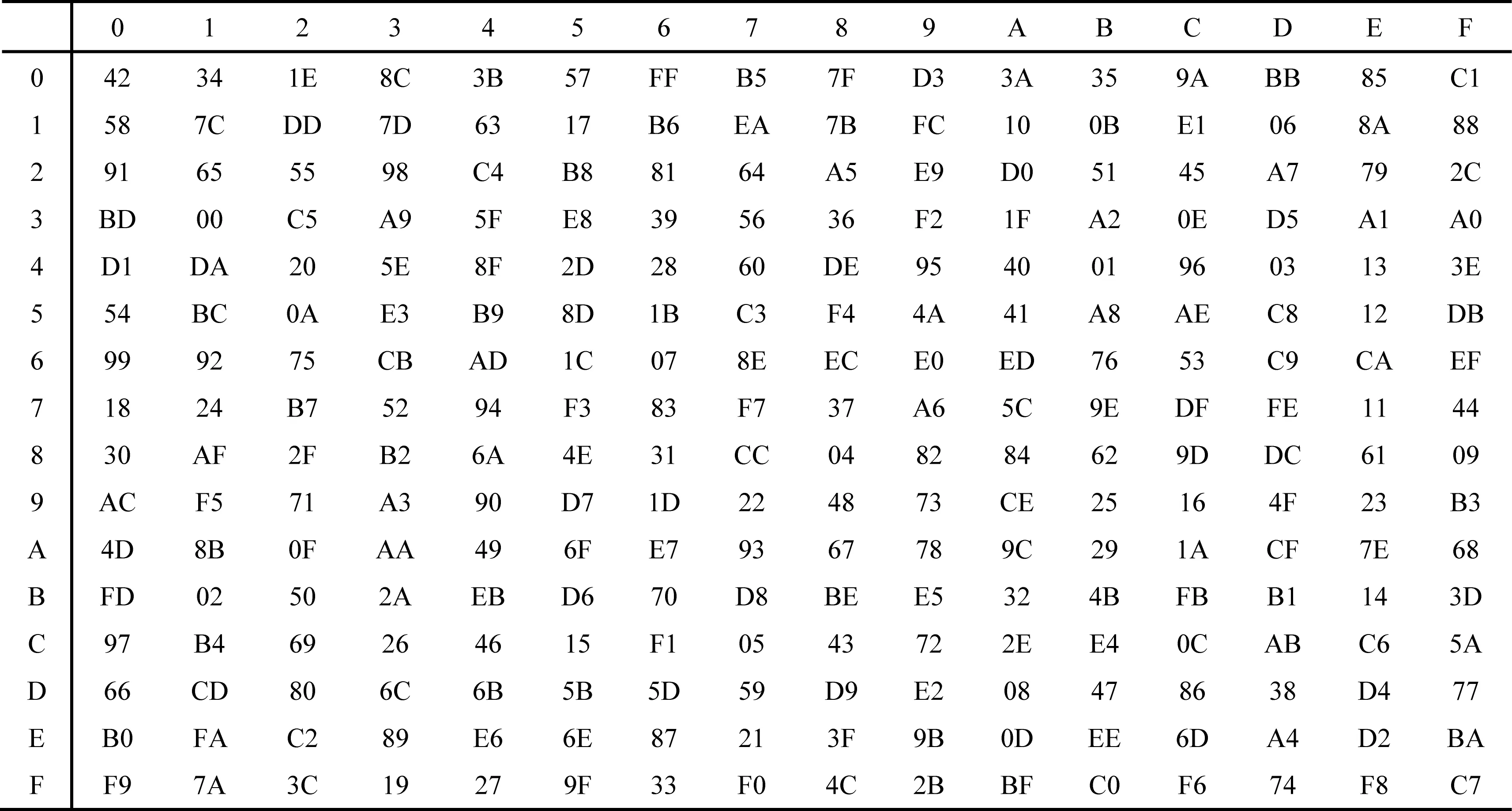
Fig. 4 An example of the reconstructed S-box圖4 重構后的S盒示例

3 算法安全性分析

3.1 S盒安全性分析

本文所設計的S盒的構造過程可分為2部分：第1部分為基于復合混沌系統的S盒設計過程；第2部分為S盒重構過程.圖5、圖6分別為基于復合混沌系統及重構后所產生S盒的LP值分布圖.

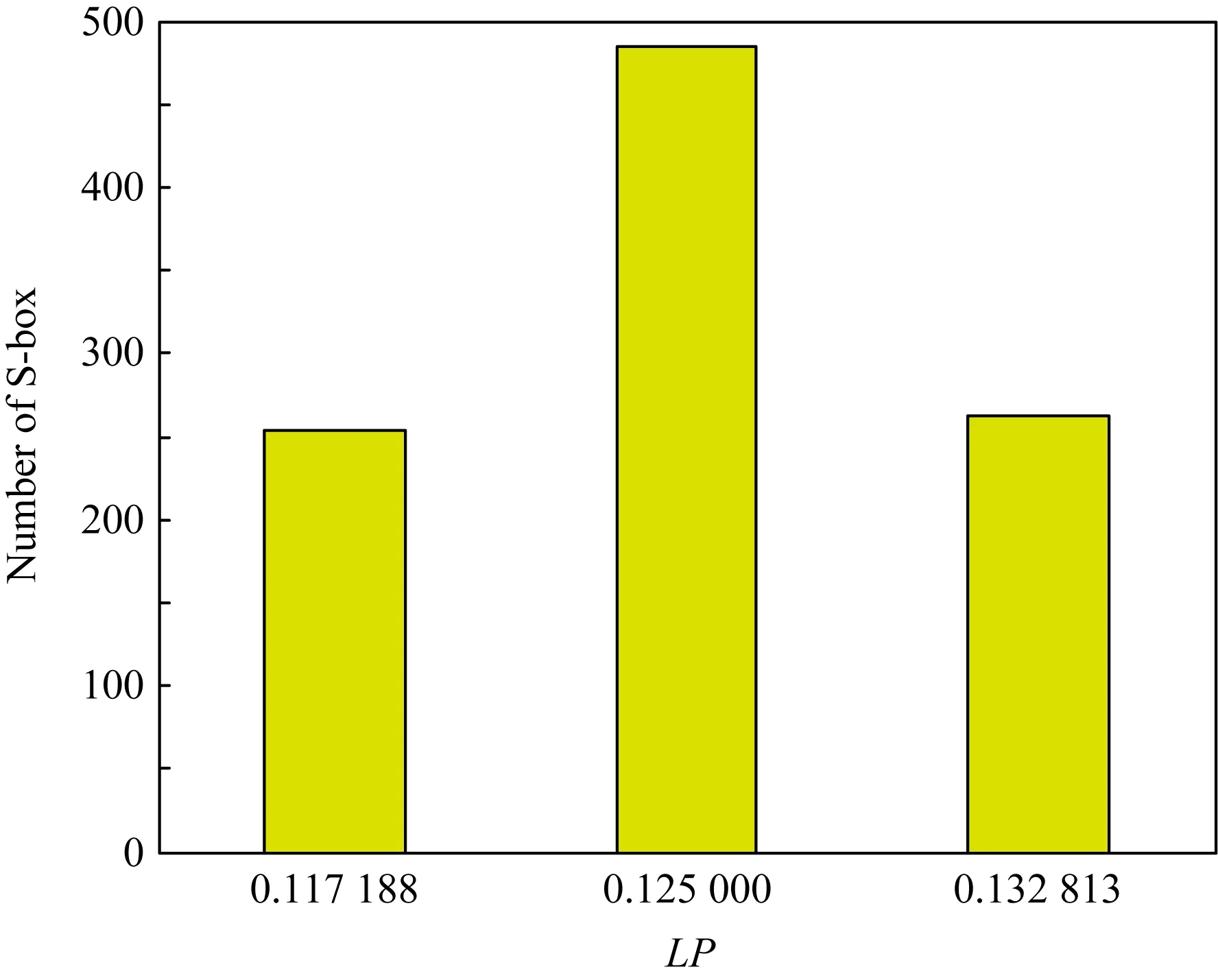
Fig. 5 LP value distribution of S-box generated based on combined chaotic systems圖5 基于復合混沌系統生成S盒的LP值分布

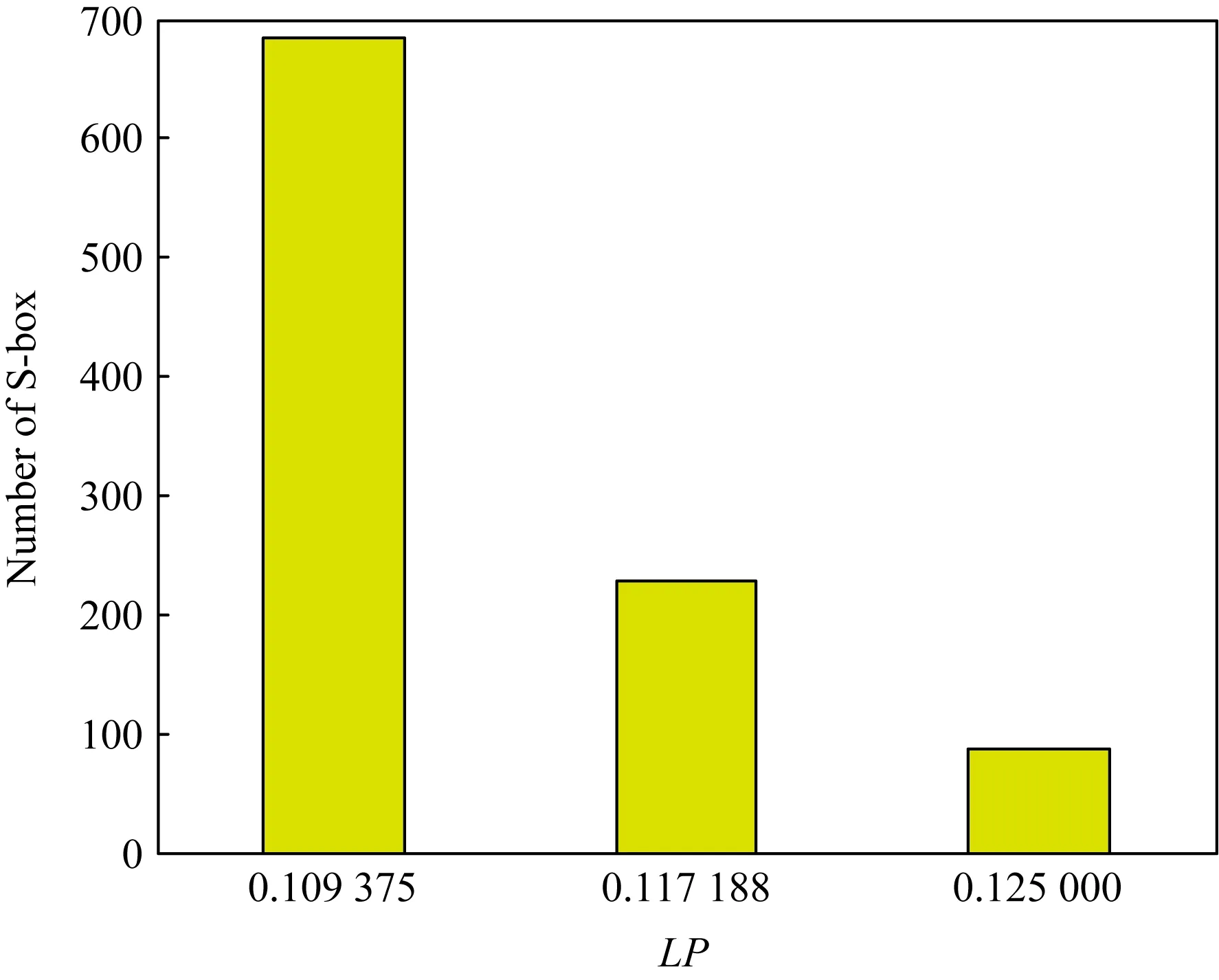
Fig. 6 LP value distribution of the refactored S-box圖6 重構后S盒的LP值分布

在這1 000個S盒中，混沌系統所產生的S盒的LP值的主要集中在0.125 000，而重構后的S盒的LP值的主要集中在0.109 375.由此可見，經過Arnold映射置亂重構后的S盒具有更好的非線性特性.

本文選取上述重構后性能最優的一個S盒作為分析對象，同時選取了其他3種同類的性能優良的S盒進行對比分析，分別是文獻[12-13]以及ZUC算法中所涉及的S盒.其中，ZUC算法有2個不同的S盒，本文選取其中一個為例，即S0盒，對6項性能指標的分析均按照選取的對象進行比對.

3.1.1 雙射特性

根據判斷S盒滿足雙射特性的充要條件，可知本文構造的8×8的S盒，其分量布爾函數的線性運算和的平均值是128，最大值和最小值也都是128，如表1所示.經過對比可見，本文產生的S盒均符合雙射特性的判斷標準.

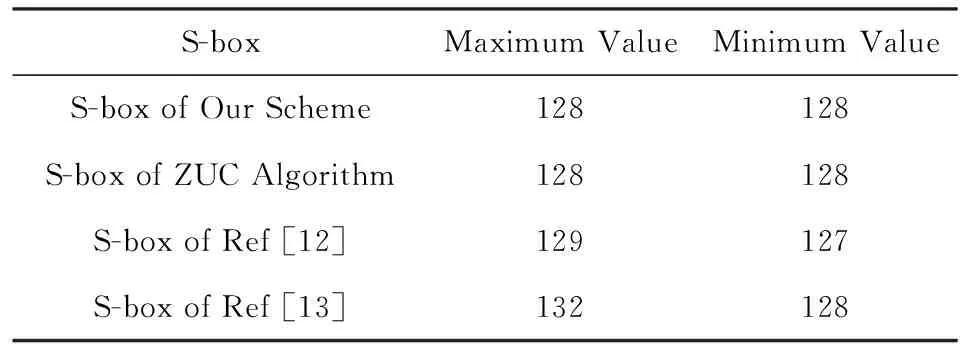
Table 1 Comparison of the S-box Bijective Properties表1 S盒雙射特性對比

3.1.2 非線性度

在實際應用中，計算布爾函數f(x)的非線性度一般通過Walsh-Hadamard變換實現.本文應用Walsh譜表示f(x)的非線性度，具體表達式為

(13)

其中，x·ω表示x與ω的點積.

在密碼分析中，非線性度Nf與抗線性攻擊正相關，Nf越大表明其能力越強，即S盒的抗線性分析性越好.本文利用式(4)和式(13)計算本文所構造S盒的非線性度，最大值為106.通過表2所示的對比結果可知，本文所構造的S盒在抵抗線性密碼分析方面性能良好.

Table 2 Comparison of the S-box Nonlinearity表2 S盒非線性度對比

3.1.3 嚴格雪崩準則(SAC)

嚴格雪崩準則是用來描述序列輸入和輸出變化相關性的重要標準.Webster等人[19]提出了適用于S盒性能評價的計算方法.因此，一般使用相關矩陣中元素的平均值來衡量S盒是否滿足該準則，若相關矩陣的元素值越趨近于0.5，則表明S盒越滿足嚴格雪崩準則.本文所構造出的S盒相關矩陣的平均值與其他文獻中S盒對比結果如表3所示，可見本文所構造的S盒與0.5更接近，因此性能更好.

Table 3 Comparison of the Mean Values on S-box Correlation Matrix

3.1.4 輸出比特間獨立性(BIC)

輸出比特間獨立性一般用于判斷，如果2個雪崩分量獨立不相關，說明此時S盒具有良好的隨機性.S盒的布爾函數分量可表示成f0,f1,…,fn，若S盒滿足BIC-SAC，則fj⊕fk(j≠k,1≤j,k≤n)應滿足嚴格雪崩準則.如果S盒的BIC-SAC值逼近于0.5，說明其隨機性良好，并且越接近這一逼近值性能越好.本文所構造的S盒的BIC-SAC值的平均值為0.504 9，與其他文獻中的S盒相比可見，其具有相對較好的BIC特性.與其他同類方案相比，得到的對比結果如表4所示:

3.1.5 差分均勻性

衡量S盒抗差分密碼攻擊性能時，通常使用差分逼近概率DPf這一重要指標.DPf值與抗差分攻擊能力反相關，值越小說明抗差分攻擊能力越強.由式(5)可以計算出本文構造S盒的差分分布最大值是10，即DP=0.039 062 5.與其他文獻所構造S盒的DP值對比結果如表5所示:

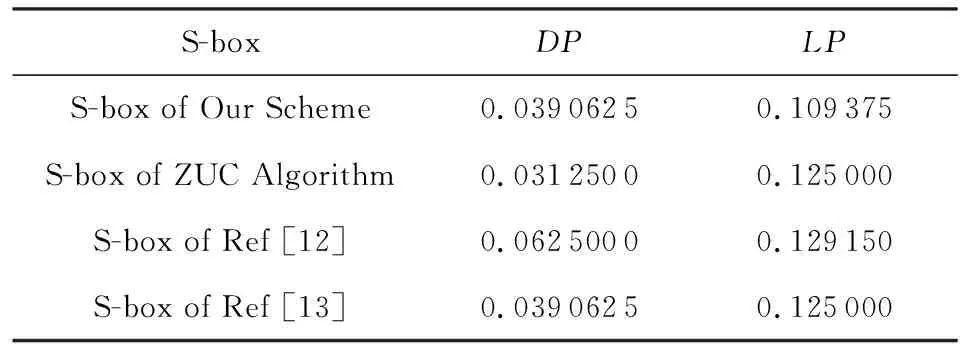
Table 5 Comparison of DP and LP Values on S-box表5 S盒的DP,LP值對比

3.1.6 線性逼近概率

線性逼近概率LPf通常用來證明S盒抵抗線性密碼攻擊的能力，LPf也與抵抗線性攻擊的能力反相關，值越小越能說明抵抗線性攻擊的能力強.本文構造的S盒的LPf值根據式(6)～(8)進行計算.最后，S盒的DPf和LPf，與其他文獻中構造的S盒的DPf和LPf對比如表5所示.可見，本文構造的S盒具有較小的差分概率及線性概率，能有效抵抗差分密碼攻擊及線性密碼攻擊.

3.2 基于混沌系統的ZUC算法安全性分析

ZUC算法是一個面向字設計的序列密碼，分析序列密碼安全性的核心是檢驗其密鑰流序列的隨機性.NIST檢測方法[24]為序列密碼的安全測評提供了理論分析的數據基礎，不僅可以減少一定的工作量，同時可以暴露出理論分析無法發現的安全漏洞.因此，本文選用NIST隨機性檢測方法分別對ZUC算法以及基于本文所構造的混沌S盒的優化ZUC算法進行安全性測試，如果測試結果的P-value值均大于0.01，則可證明算法通過測試.

3.2.1 密鑰序列生成

在密碼學中，當一個算法初始密鑰和初始向量均設置為“0”，將會生成隨機性最差的密鑰流[25].如果此時產生的序列能通過隨機性檢測，則意味著它在其他情況下也可以通過測試.因此，本文通過設置初始密鑰、初始向量為“0”進行測試，同時選取密鑰字個數為40 000.此時，我們便可以得到2個40 000×32 b的密鑰流序列，分別對應的是ZUC算法及本文所設計的基于混沌S盒的ZUC算法，然后以二進制表示形式分別存入文件key1.txt和key2.txt中作為待測序列.

3.2.2 sts-2.1.2軟件隨機性檢測

在Windows系統下安裝“sts-2.1.2”和“cygin”軟件，進入測試包所在目錄進行測試，ZUC算法以及基于本文所構造的混沌S盒的優化ZUC算法的NIST測試結果對比如表6所示:

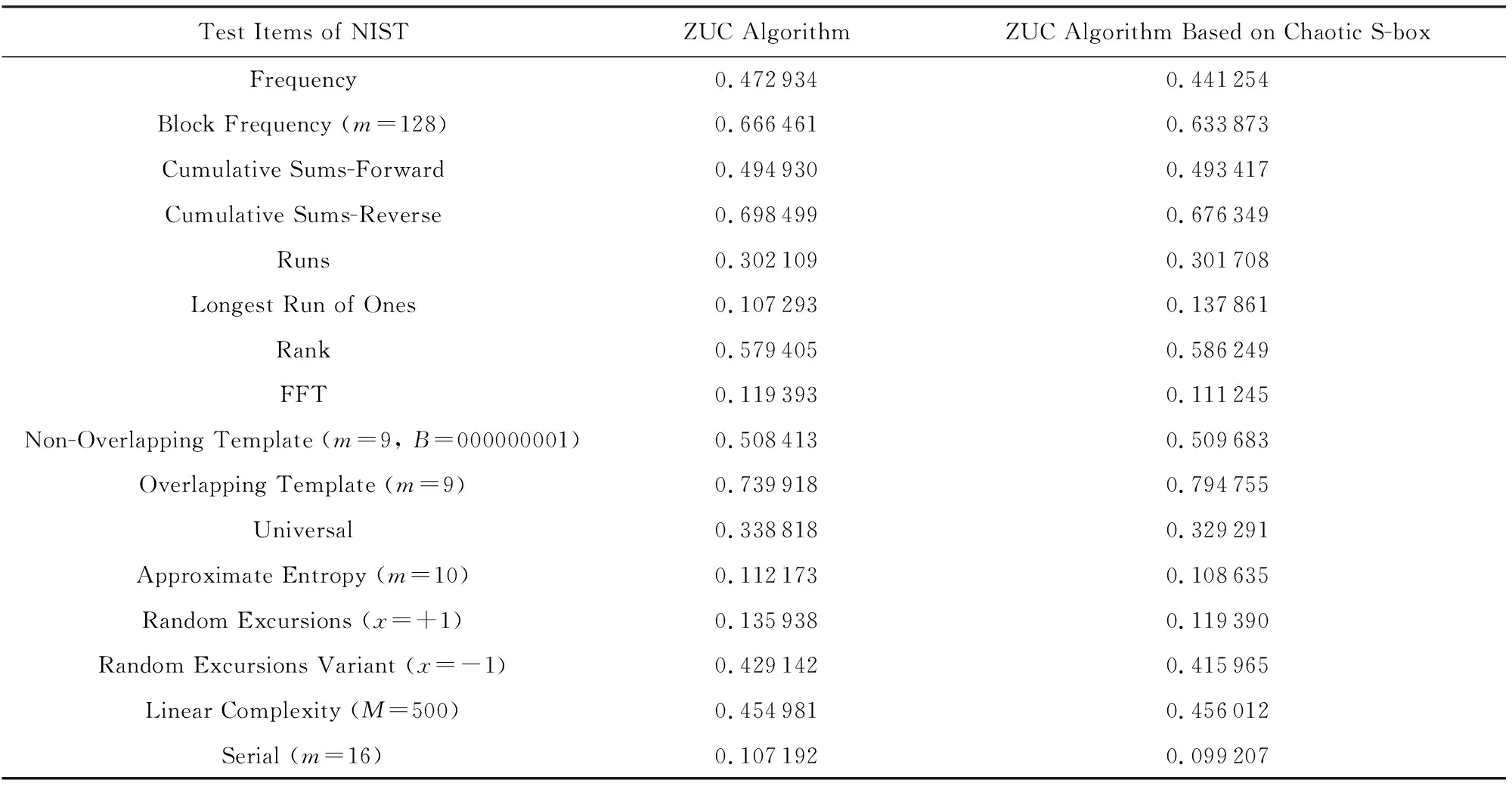
Table 6 P-value Comparison of NIST Test Results表6 NIST測試P-value值結果對比

由表6可以看出，基于混沌S盒的ZUC算法的16項測試項的結果顯著，所有P-value值均大于顯著水平α(其中α=0.01)，且全部優于ZUC算法本身.因此，基于混沌S盒的ZUC算法生成的密鑰流序列隨機性較好.

3.3 基于混沌S盒的ZUC算法的實現及性能分析

3.3.1 算法實現

本文通過使用標準C語言對算法進行軟件實現，然后再將其移植至單片機上，軟件實現的結果如圖7所示，圖中所展示的是基于混沌S盒的ZUC算法的部分密鑰序列.

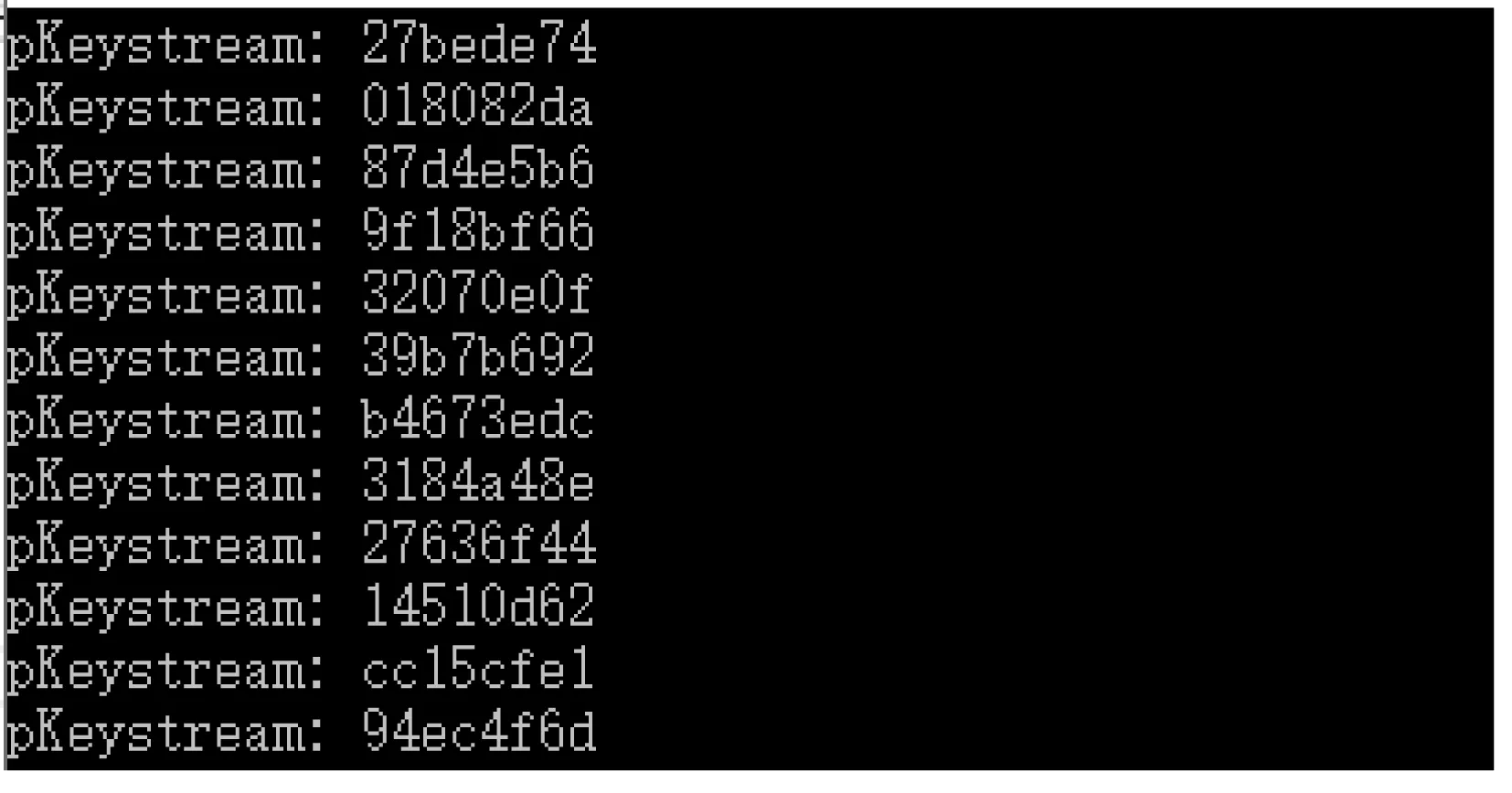
Fig. 7 Partial key sequence of ZUC algorithm based on chaotic S-box圖7 基于混沌S盒的ZUC算法部分密鑰序列

3.3.2 算法性能分析

對于基于混沌思想的S盒設計而言，還要考慮其軟硬件的實現性能.本文分別對基于混沌S盒的ZUC算法的軟硬件實現性能進行了測試.

本文的軟件實現利用PC機進行，其中PC機的操作系統為Windows 10 64 b，CPU為Intel?CoreTMi5-3337U@1.80 GHz，RAM為8 GB，通過Visual Studio2012編程軟件進行測試，按照基于混沌思想的S盒設計方案替換ZUC算法中的固定S盒，分別從代碼大小、運行時間和系統占比3個方面進行性能對比和分析.從表7可以看出，增加動態S盒部分的設計之后，代碼大小增長了40%，占系統RAM百分比增長了0.3，但運行時間僅增加0.01 s，對算法本身的運行性能并未產生很大的影響，在可接受范圍內.

Table 7 Algorithm Software Implementation Performance表7 算法軟件實現性能

本文的硬件實現采用ATmega8A型8 b微控制器，片內SRAM為512 KB，同樣按照設計方案分別從代碼大小、運行時間和系統占比3個方面進行了性能的對比和分析.從表8可以看出，在本文的硬件運行環境下，相較于軟件實現而言，ZUC算法本身的代碼大小變大.這是由于單片機本身的通信接口等定義，占用了一小部分存儲空間，但與算法本身所需存儲空間相比，可忽略不計.在加入混沌動態S盒設計之后，代碼大小增加了38%，占系統RAM百分比增長了3，運行時間僅增加0.11 s.但這是由于單片機的性能遠不如PC機，對算法的硬件實現效率來講并未產生很大的影響，完全在可以接受的范圍內.

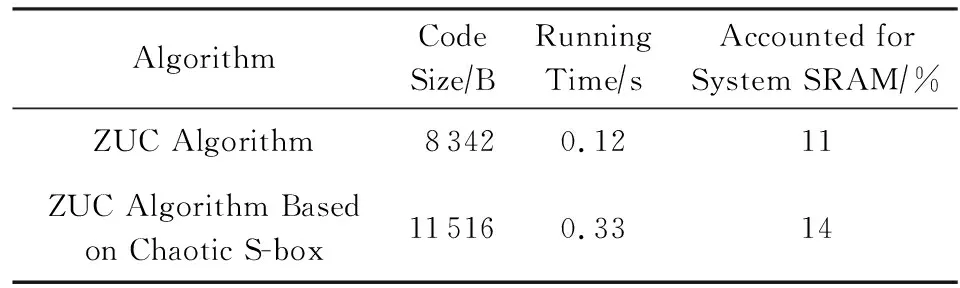
Table 8 Algorithm Hardware Implementation Performance表8 算法硬件實現性能

基于混沌S盒的ZUC算法的軟硬件性能測試表明，該方案不僅提高算法的安全性, 也具有較好的軟硬件可實現性.

3.3.3 算法的應用場景

本文將基于混沌S盒的ZUC算法應用于自己搭建的輕量級物聯網平臺中，對整個物聯網平臺系統中的感知層資源受限設備所采集的數據進行加密，并將密文數據傳輸并存儲在物聯網平臺的數據庫中，便于合法授權用戶進行數據的統一管理，提高了數據在采集、傳輸及存儲全流程的安全性.

通過使用超級終端對數據采集和傳輸的過程進行監控，可以看到經過單片機后數據已經被加密，傳輸過程中的數據為密文形式，如圖8所示：

Fig. 8 Ciphertext transmission of data圖8 數據的密文傳輸

數據上傳至平臺端，也是以密文形式在數據庫中進行存儲，如圖9所示：

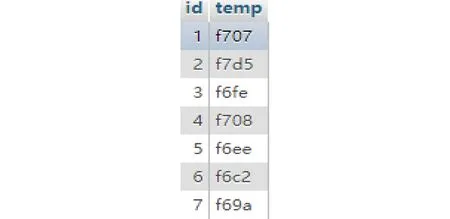
Fig. 9 Data of ciphertext stored in the database圖9 數據庫中密文形式的數據存儲

4 結 論

本文所提出的S盒設計方法是基于2個經典混沌系統的復合，并將Arnold映射引入方案設計中進行二次置亂和重構.通過將本文構造的S盒嚴格按照S盒設計準則進行安全性分析，并與前人所提出的方法做了充分比較，驗證了本文所構造S盒的密碼特性.安全性分析結果表明:此方案產生的S盒相比于ZUC算法及其他相關文獻具有更高的安全性，并能實現動態生成性能良好的S盒，替換ZUC算法中的2種固定的S盒.最后，本文對基于混沌S盒的ZUC算法進行了NIST隨機性測試和軟硬件性能測試，結果表明:本文所構造的S盒安全性更高，不僅增強了ZUC算法所產生密鑰流序列的隨機性，還兼具較好的軟硬件可實現性，可應用于資源受限的物聯網設備中的數據加密過程.