無配對公鑰認證可搜索加密方案

楊寧濱 周 權 許舒美

(廣州大學數學與信息科學學院 廣州 510006)

云計算高速發展以及5G通信應用的推廣下，云存儲服務受到了人們的廣泛關注.人們可以將自己的電子郵件、個人健康記錄和財務信息等數據上傳到云端，與他人共享或在任何地方使用.顯然，云計算給人們帶來了很多方便.但是，這存在著數據隱私性的安全問題.用戶在上傳數據到云端后，數據的所有權則由云端的服務器所管理，這可能存在云端服務器不完全可信的狀態下導致數據泄露.用戶不能完全地控制自己上傳的數據安全性，這遠遠不能滿足數據云端安全的實用性.

Boneh等人所提出的方案是需要在秘密通道下才可以安全傳輸數據到云服務器.但是，一旦攻擊者截獲秘密通道傳輸的數據，用戶的隱私數據則會被竊取.Baek等人[3]對此研究并提出了公共通道的PEKS方案，解決了Boneh等人的方案中存在的隱私性問題.之后，Huang等人[4]提出的PAEKS方案滿足了陷門不可區分性，但是該方案在文獻[5]中被指出不滿足密文不可區分性.攻擊者可以公開地對關鍵詞密文進行對等測試.因此，方案抵抗外部攻擊者與內部攻擊者的關鍵詞猜測攻擊，是實現方案的關鍵詞安全性的充要條件.

目前多數的公鑰可搜索加密方案是基于雙線性對運算所設計的.這在資源能力有限的設備上執行會降低其運算效率，從而影響用戶雙方的交互體驗.為了提高用戶與云端服務器交互的效率以及滿足關鍵詞隱私安全性，提出一個非雙線性對運算的帶關鍵詞的公鑰認證加密方案.

本文主要貢獻包括3個方面：

1) 提出一個基于非雙線性對運算下的公共通道的公鑰認證可搜索加密方案(NBP-SCF-PAEKS)，相對于雙線性對運算的方案效率大大提高.該方案是基于用戶雙方密鑰協商構造的，從而具備訪問控制的功能，即具備一定的認證功能.

2) 通過無隨機預言機模型下使用Game-Hopping方案證明該方案滿足適應性選擇關鍵詞攻擊下多關鍵詞密文的不可區分性以及適應性選擇關鍵詞攻擊下的陷門不可區分性，從而使該方案達到抵抗離線內部攻擊者的關鍵詞猜測攻擊以及在線外部攻擊者的關鍵詞猜測攻擊的安全性.

3) NBP-SCF-PAEKS方案與SCF-PEKS[3]，PAEKS[4]，SCF-PEPCKS[6]，Hwang等人方案[7]以及PAEKSR[8]方案的計算效率和存儲大小進行仿真比較，實驗結果是方案的計算效率相對于其他比較的方案要高，并且所需存儲內存較小.

1 相關工作

文獻[1]中Song等人是最先提出可搜索加密的方案，但是該方案需要遍歷所有文件才可以返回搜索結果，因此需要花費較大計算代價；文獻[2]中Boneh等人介紹了帶關鍵詞的公鑰可搜索加密方案(PEKS)，但不久之后，研究者發現了PEKS方案明顯的缺陷，關鍵字陷門需要秘密傳輸到云服務器；文獻[3]中Baek等人針對PEKS方案提出了一個在公共通道下實現的公鑰可搜索加密方案(SCF-PEKS)，解決PEKS[2]中存在的缺陷；Yau等人[9]研究離線關鍵詞猜測攻擊，并且表明容易遭受內部敵手攻擊；文獻[10]中Fang等人提出了在不使用隨機預言機模型下證明SCF-PEKS方案的關鍵詞安全性.但是PEKS和SCF-PEKS方案都存在著關鍵詞的隱私性問題.當攻擊者為指定服務器時，易遭受關鍵詞猜測攻擊.因此，公鑰可搜索加密中關鍵詞的隱私性成為研究者所需要解決的問題.文獻[11]中Emura等人提出了自適應安全的無安全通道的公鑰可搜索加密的通用構造方案；Rhee等人在文獻[12]中引入了“陷門不可區分性”概念，并證明了這是抵抗關鍵詞猜測攻擊的一個充分條件.根據攻擊模式可以分為關鍵詞在線猜測攻擊與關鍵詞離線猜測攻擊；文獻[13]中Noroozi等人提出了新的PEKS方案來抵抗外部攻擊者的離線與在線關鍵詞攻擊.

根據攻擊者的類型可分為外部攻擊者和內部攻擊者.內部攻擊者一般指的是半可信云服務器，外部攻擊者一般指的是除數據提供及使用的雙方用戶與服務器外的攻擊者.由于半可信服務器被允許對關鍵詞密文及關鍵詞陷門做匹配測試，所以半可信的服務器比外部攻擊者的權限更大.文獻[4]中Huang等人介紹其方案(PAEKS)滿足抵抗內部攻擊者的關鍵詞猜測攻擊.其主要工作是對關鍵詞加密時引入發送者的私鑰，實現公鑰認證加密功能，但是這個方案的陷門是固定的，且被指出不滿足密文不可區分性[5].文獻[7]中Hwang等人提出對ElGamal改進下的非雙線性對下的公鑰可搜索加密，能夠抵御外部攻擊者的關鍵詞猜測攻擊.文獻[4,14-15]中徐海琳等人及陸陽等人采用借助雙方的公私鑰產生密鑰協商的關鍵詞密文與陷門，只有認證的用戶才能實現密文與陷門的產生，并且能夠抵御已知的3種關鍵詞猜測攻擊.文獻[8]中Qin等人指出了Huang等人的PAEKS方案的關鍵詞隱私性不足，在選擇明文攻擊不允許敵手公開質詢消息密文，并且不能滿足多關鍵詞密文猜測攻擊.在此基礎上改進后提出可認證的帶關鍵詞的公鑰加密方案(PAEKSR)，同時滿足多關鍵詞密文不可區分性安全.

文獻[16]中Chen等人介紹了一種新型的抵抗內部攻擊者離線關鍵詞猜測攻擊的公鑰可搜索加密，即輔助服務器的公鑰可搜索加密.該方案是借助服務器提供關鍵詞的盲簽名，并返回給用戶再進行PEKS加密，服務器的盲簽名的密鑰具備密鑰更新的功能，使得方案更具靈活性，并且引入限速機制來抵抗在線關鍵詞猜測攻擊.Zhang等人[17]在此工作基礎上推廣到區塊鏈的公鏈上應用，并且能夠抵抗已知的關鍵詞猜測攻擊.文獻[18]中Dent提出的Game -Hopping方法是一種驗證密碼方案安全性的方法，攻擊者在特定的攻擊環境中運行一個未知的成功概率，隨著調整攻擊環境不斷計算，直到計算出攻擊者成功的概率，利用這個臨界值來判斷方案的安全性.

之后，研究者針對公鑰可搜索加密方案設計具有不同功能的方案，其中有可驗證的關鍵詞可搜索加密[19-21]、模糊關鍵詞的可搜索加密[22]、基于屬性加密的帶關鍵字搜索方案[23-24]以及基于代理重加密的帶關鍵字搜索方案[25]等.

2 預備知識

本節主要介紹困難性假設，并對關鍵詞猜測攻擊類型進行分析.

2.1 困難性假設

|Pr[A(g,ga)=a]|<ε.

|Pr[A(G,q,g,ga,gb,Z)=1]-
Pr[A(G,q,g,ga,gb,H(ga b))=1]|<ε.

2.2 關鍵詞猜測攻擊類型分析

本節主要對Baek等人提出的SCF-PEKS方案中存在在線模式下外部攻擊者關鍵詞猜測攻擊和離線模式下內部攻擊者關鍵詞猜測攻擊進行描述.

在線模式下外部攻擊者關鍵字猜測攻擊[6]是由外部攻擊者執行攻擊，攻擊步驟為：

1) 在在線模式下，外部攻擊者首先確定攻擊對象(目標接收方).

2) 外部攻擊者準備想要執行攻擊的關鍵詞集{w1,w2,…,wn}，借助被攻擊對象的公鑰執行SCF-PEKS的加密算法生成所有可能與文件密文對應的關鍵詞密文，即Cf,Cwi，并且維護列表{wi,Cwi,Cf}.

3) 外部攻擊者將密文集合傳輸到云服務器.攻擊者監視云服務器和目標接收方之間的通信.當目標接收方生成關鍵詞陷門Tw發送至云服務器檢索時，由于在公共信道傳輸，外部攻擊者可以截獲關鍵詞陷門.一旦發現返回的搜索結果與之前注入的密文集合相關，對照維護的列表，外部攻擊者就可以獲取目標接收方正在搜索的關鍵字信息，從而獲取用戶搜索的關鍵詞信息.

離線模式下內部攻擊者關鍵詞猜測攻擊[6]是由內部攻擊者(一般為惡意服務器)執行的.攻擊步驟為：

1) 在離線模式下，內部攻擊者首先確定攻擊對象(目標接收方).

2) 內部攻擊者接收到目標接收方的關鍵詞陷門Tw后，準備想要執行猜測攻擊的關鍵詞w，借助目標接收方的公鑰信息以及服務器公鑰信息執行SCF-PEKS加密算法產生關鍵詞密文Cw.

3) 內部攻擊者擁有了關鍵詞陷門Tw以及關鍵詞密文Cw后，執行測試實驗，直到攻擊者猜測成功，否則返回步驟2)重新執行.

3 方案定義與安全模型

本節給出一個能夠抵抗在線外部攻擊者關鍵詞猜測攻擊以及離線內部攻擊者關鍵詞猜測攻擊的安全性的方案定義，即非雙線性對運算下公共通道帶關鍵詞搜索的公鑰認證加密方案的定義(Non Bilinear Pairs SCF-PAEKS, NBP-SCF-PAEKS)，并且給出方案的安全模型.

3.1 方案定義

圖1所示為NBP-SCF-PAEKS方案的系統框架.系統框架包括4個主體：授權中心(authorization center, AC)、數據擁有者(data owner, DO)、數據使用者(data user, DU)以及云服務提供者(cloud service provider, CSP).

Fig. 1 The scheme system framework圖1 方案系統框架

授權中心AC主要職能是分發全局參數給系統框架內的其他主體.由于DO的本地存儲能力有限，只能將帶有關鍵詞w索引的文件加密進行存儲于CSP，即DO通過Encrypt算法加密產生關鍵詞密文，與加密的文件一起存儲于CSP中.當DU想要檢索帶關鍵詞w的文件時，通過Trapdoor算法產生搜索陷門傳至CSP，由CSP檢索并通過Test算法驗證是否存在匹配的關鍵詞的文件.最后把搜索結果返回給DU.若匹配成功，則返回加密的文件給DU.DU解密即可獲取明文文件.

NBP-SCF-PAEKS方案由5個多項式時間算法組成：

1)GlobalSetup(λ).該算法由授權中心AC執行，輸入安全參數λ，輸出全局公共參數GP.

2)KeyGen(GP).該算法由DO與DU分別執行完成，輸入全局公共參數GP，DO輸出公私鑰對skS與pkS，而DU輸出公私鑰對skR與pkR.

3)Encrypt(GP,skS,pkR,w).該算法由DO執行，輸入全局參數GP、關鍵詞w、DO私鑰skS、DU公鑰pkR，輸出關鍵詞密文Cw，DO將關鍵詞密文Cw與加密的文件Cf傳至CSP中存儲.

4)Trapdoor(GP,skR,pkS,w′).該算法由DU執行，輸入全局參數GP、檢索的關鍵詞w′、DU私鑰skR以及DO的公鑰pkS，輸出搜索陷門Tw′.

5)Test(GP,Cw,Tw′).CSP收到DU的搜索陷門Tw′，對關鍵詞密文Cw與搜索陷門Tw′測試.若匹配成功，則輸出1，并返回文件密文數據；否則輸出0.

3.2 安全模型

Boneh等人首先引入了密文不可區分性的概念，它旨在防止外部攻擊者在不知道關鍵字測試陷門的情況下獲取加密文件中包含的任何關鍵字信息.而Qin等人[8]在此基礎上延展提出多密文不可區分性.而陷門不可區分性保證了給定一個未知關鍵字的測試陷門，內部攻擊者無法獲得關于關鍵字的任何有用信息.

在2.2節所討論的在線模式下外部攻擊者關鍵詞猜測攻擊與離線模式下內部攻擊者的關鍵詞猜測攻擊是目前公鑰可搜索加密中需要解決的安全性問題.而本文所提出的公鑰認證可搜索加密方案則可以抵抗這2類攻擊，值得注意的是，由于方案的正確性，避免了外部攻擊者的存在.假設NBP-SCF-PAEKS方案中存在一個外部攻擊者，由該方案正確性定義可知，攻擊者若生成了可被關鍵詞陷門匹配的可搜索密文，則該攻擊者是數據使用者(DU)所認可的數據擁有者(DO)，與它是外部攻擊者相矛盾.這限制了外部攻擊者攻擊的可能，使得方案更具安全性.

因此，提出NBP-SCF-PAEKS方案需要同時滿足2點：1)適應性選擇關鍵詞攻擊下的多關鍵詞密文不可區分性(multi-keyword ciphertext indisting-uishability under the adaptive chosen keyword attack, MKC-IND-CKA);2)適應性選擇關鍵詞攻擊下的關鍵詞陷門不可區分性(keyword trapdoor indisting-uishability under the adaptive chosen keyword attack, KT-IND-CKA).MKC-IND-CKA保證敵手不能區分其挑戰的2個關鍵詞集的密文，而KT-IND-CKA則保證敵手不能區分其挑戰的2個關鍵詞陷門.針對公鑰認證可搜索加密方案，敵手可分為2類：外部攻擊者與內部攻擊者.這里定義外部攻擊者為除DO,DU以及CSP之外的攻擊者，內部攻擊者為惡意的CSP.

Game MKC-IND-CKA：

Adv(λ)MKC-IND=|Pr[b=b′]-12|.

定義3.若不存在多項式時間敵手能夠以不可忽略的優勢贏得上述Game MKC-IND-CKA，則可認為本方案滿足適應性選擇關鍵詞攻擊下的多關鍵詞密文不可區分性安全.

Game KT-IND-CKA：

1) 系統初始化.與Game MKC-IND-CKA的初始化階段一致.

2) 詢問階段1.與Game MKC-IND-CKA的第一階段詢問一致.

Adv(λ)KT-IND-CKA=|Pr[b=b′]-12|

定義4.若不存在多項式時間敵手能夠以不可忽略的優勢贏得上述Game KT-IND-CKA，則可認為本方案滿足適應性選擇關鍵詞攻擊陷門不可區分性.

4 方案描述

在3.1節給出了NBP-SCF-PAEKS方案的定義，其5個時間算法具體描述為：

4)Trapdoor(GP,skR,pkS,w′).DU選定需要搜索的關鍵詞w′，計算搜索陷門Tw′=g-skR2×H(w′‖ss1)，其中ss1=H1((pkS1)skR1).并將其上傳至CSP檢索.

5)Test(GP,Cw,Tw′).CSP收到DU的搜索陷門Tw′后，計算H1(C1×Tw′)=C2是否成立，若成立則輸出1并返回文件密文數據，否則返回0.

方案正確性：

ss=H1((pkR1)skS1)=H1((pkS1)skR1)=ss1；

若w′=w，則等式H1(C1×Tw′)=C2成立，故方案正確有效.

5 安全性證明

本節參考文獻[6]以及Game-Hopping[18]方法給出NBP-SCF-PAEKS方案在無隨機預言機模型下的安全性證明.下面需要使用差別引理[18]：

引理1[18].定義S1,S2,E為3個不同的事件且E為錯誤事件，使得事件S1|E發生當且僅當在事件S2|E發生時，有：

|Pr[S1]-Pr[S2]|≤Pr[E].

定理1.若Hash函數H滿足抗碰撞性、群G上DL假設是困難以及多項式時間內有限的n個關鍵詞查詢，則所提出方案滿足適應性選擇關鍵詞攻擊下多關鍵詞密文不可區分性的安全.

Game-Hopping方法的證明過程如下：

AdvMKC-IND-CKA=|Pr[X0]-12|.

Pr[X1]=Pr[X0].

ss=H1((pkR1)skS1).

ss1=H1((pkS1)skR1).

ss1=H1((pkR1)skS1).

Pr[X2]=Pr[X1].

|Pr[X2]-Pr[X3]|≤2n×AdvH.

AdvMKC-IND-CKA=|Pr[X4]-12|.

AdvMKC-IND-CKA=|Pr[X0]-12|≤
|Pr[X0]-Pr[X1]|+|Pr[X1]-Pr[X2]|+
|Pr[X2]-Pr[X3]|+|Pr[X3]-Pr[X4]|+
|Pr[X4]-12|.

因此，綜合上述的游戲方程，可以得出如下結論：

AdvMKC-IND-CKA=n×AdvDL+ 2n×AdvH.

本文在多項式時間內n個(多)關鍵挑戰密文查詢且基于Hash函數H是抗碰撞的并且基于離散對數DL的困難假設下，AdvMKC-IND-CKA是可忽略的，即本方案滿足適應性選擇關鍵詞攻擊下的多關鍵詞密文不可區分性.

證畢.

定理2.若Hash函數H滿足抗碰撞性且群G上HDH假設是困難的，則所提出方案滿足適應性選擇關鍵詞攻擊的陷門不可區分性的安全性.

Game-Hopping方法的證明過程為：

AdvKT-IND-CKA=|Pr[X0]-12|.

Pr[X1]=Pr[X0].

ss1=H1(ga b).

ss1=H1(ga b).

ss1=H1(ga b).

因此，挑戰陷門Twb為有效陷門.

Pr[X2]=Pr[X1].

4) 游戲Game3.該游戲定義與定理1證明中Game3相同.

|Pr[X2]-Pr[X3]|≤2AdvH.

|Pr[X3]-Pr[X4]|≤AdvHDH.

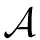
AdvKT-IND-CKA=|Pr[X4]-12|.

AdvKT-IND-CKA=|Pr[X0]-12|≤
|Pr[X0]-Pr[X1]|+|Pr[X1]-Pr[X2]|+
|Pr[X2]-Pr[X3]|+|Pr[X3]-Pr[X4]|+
|Pr[X4]-12|.

綜合上述的游戲方程，可以得出結論：

AdvKT-IND-CKA=AdvHDH+ 2AdvH.

由于Hash函數H是抗碰撞的并且基于HDH的困難假設下，AdvKT-IND-CKA是可忽略的，即本方案滿足適應性選擇關鍵詞攻擊陷門不可區分性.

證畢.

6 性能分析

本文的NBP-SCF-PAEKS方案是設計非雙線性對下且在公共通道能夠抵抗在線外部攻擊者關鍵詞猜測攻擊和離線內部攻擊者關鍵詞猜測攻擊的公鑰認證可搜索加密方案，該方案高效安全可行.

表1給出本文方案與其他方案的功能比較.其中MKC-IND-CKA表示適應性選擇關鍵詞攻擊的多關鍵詞密文不可區分性安全，Out-online-KGA表示在線模式下外部攻擊者關鍵詞猜測攻擊 In-offline-KGA表示離線模式下內部攻擊者的關鍵詞猜測攻擊.

Table 1 Security Properties Comparison表1 安全性能比較

Table 2 Efficiency Comparison of Different Schemes表2 不同方案的效率比較

Fig. 2 Computation cost of keyword encryption and testing圖2 關鍵詞加密與驗證的計算消耗比較

Fig. 3 Communication size of keyword ciphertext and trapdoor圖3 關鍵詞密文與關鍵詞陷門通信存儲大小比較

為了直觀展示NBP-SCF-PAEKS方案與其他方案關鍵詞的運算時間消耗對比，進行了仿真實驗.實驗環境是在操作系統為Ubuntu 16.04 LTS，處理器為Intel?CoreTMi5-4210U CPU @2.40 GHz，運行內存為12 GB以及GMP庫[28]、PBC庫[29]下進行的.我們采用與文獻[6]相同的實驗條件下的512 b循環群以及SHA-256的Hash函數進行仿真.借助文獻[6]與文獻[8]仿真的SCF-PEKS,SCF-PEPCKS,PAEKS以及PAEKSR方案的關鍵詞加密與測試的數據結果進行對比.仿真對比結果如圖2所示.對于單個關鍵詞下，NBP-SCF-PAEKS方案關鍵詞加密所需的時間消耗為0.522 ms，陷門產生所需的時間消耗為0.4 ms，測試所需的時間消耗為0.02 ms.因此，該方案的3個多項式時間算法的運行時耗均在0.1毫秒級上，相對于包含雙線性運算下的SCF-PEKS[3],PAEKS[4],SCF-PEPCKS[6],PAEKSR[8]以及Hwang等人[7]方案的計算效率要高.此外，該方案在關鍵詞密文與關鍵詞陷門的存儲所需容量與SCF-PEKS[3],SCF-PEPCKS[6]以及PAEKSR[8]相等，相對于PAEKS[4]以及Hwang等人[7]方案要低，如圖3所示:

7 總結與展望

本文提出一個基于非雙線性對運算、公共通道的帶關鍵詞搜索的公鑰認證可搜索加密方案.與過去的其他方案進行功能與效率的比較，NBP-SCF-PAEKS方案具有非雙線性對的高效運算，能夠滿足抵抗離線模式下內部攻擊者的關鍵詞猜測攻擊和在線模式下外部攻擊者的關鍵詞猜測攻擊的安全性并且具有認證的功能，使得本文方案更具有應用意義，更適合于計算能力有限的設備上使用.

隨著設備的更新換代以及量子計算機的研發促使計算機的計算能力提高，導致離散對數的密碼體制下的云數據存在潛在的泄露風險.因此，構造可行性高的抗量子計算的公鑰可搜索加密是下一步工作重心.