基于PCA-貝葉斯算法的網絡輿情預測研究

王茜儀，杜明坤，孫逸飛

(江蘇警官學院，江蘇 南京 210031)

0 引言

網絡輿情，有的專家認為是民眾對管理者持有的政治態(tài)度，有的專家認為是民眾對目前社會現象的看法和觀點的總和[1]。做好輿情管控有利于提高民眾的安全感和政府部門公信力[2]。隨著網絡的快速發(fā)展，網絡輿情傳播途徑越來越多，各種輿情指標也層出不窮，指標越多越會影響人民對輿情的分析和判斷。如今輿情管理已經成為社會秩序管理不可忽視的一部分[3]。

1 基于PCA貝葉斯的網絡輿情研究

如今，隨著手機用戶，自媒體增多，網絡直播、各大視頻網站層出不窮，網絡輿情的指標非常多，單一指標已經不能對輿沒情進行判斷，如果選取多個指標對輿情進行判斷還要考慮指標的權重問題，網絡輿情各指標之間有一定的關聯，主成分分析指標之間關聯性越大，效果越好。因此，用主成分分析方法(Principal Component Analysis，PCA)對網絡輿情各指標進行降維，提取權重較高的指標，再用貝葉斯網絡模型進行預測。

首先對已獲取數據進行標準化處理。將數據N中心化，即使每個維度的數據數學期望為0，得到：

(1)

[coeff,score,latent,tsquare]=PCA(x)

(2)

COEFF是N矩陣所對應的協方差陣V的所有特征向量組成的矩陣，即變換矩陣或稱投影矩陣，COEFF每列對應一個特征值的特征向量，列的排列順序是按特征值的大小遞減排序。具體過程如下：

(3)

由T的特征方程可以求得n個非0特征根λi(i∈[1,m])，將這些特征根從大到小排列得到：λ1≥λ2≥……≥λm>0。

(1)latent貢獻率。

(2)score是對主分的打分，投影之后的數據，也就是說原X矩陣在主成分空間的表示。每一列表示一個主成分。

(3)latent'將列轉置為行。

(4)y=(100*latent/sum(latent))'計算每個主成分貢獻率(百分數化)。

(5)B=X*coeff(:,1:r)選擇主成分對數據進行還原(經中心化處理，所以有負數)。

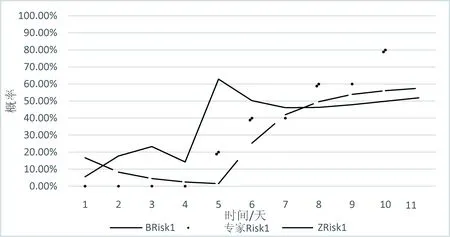
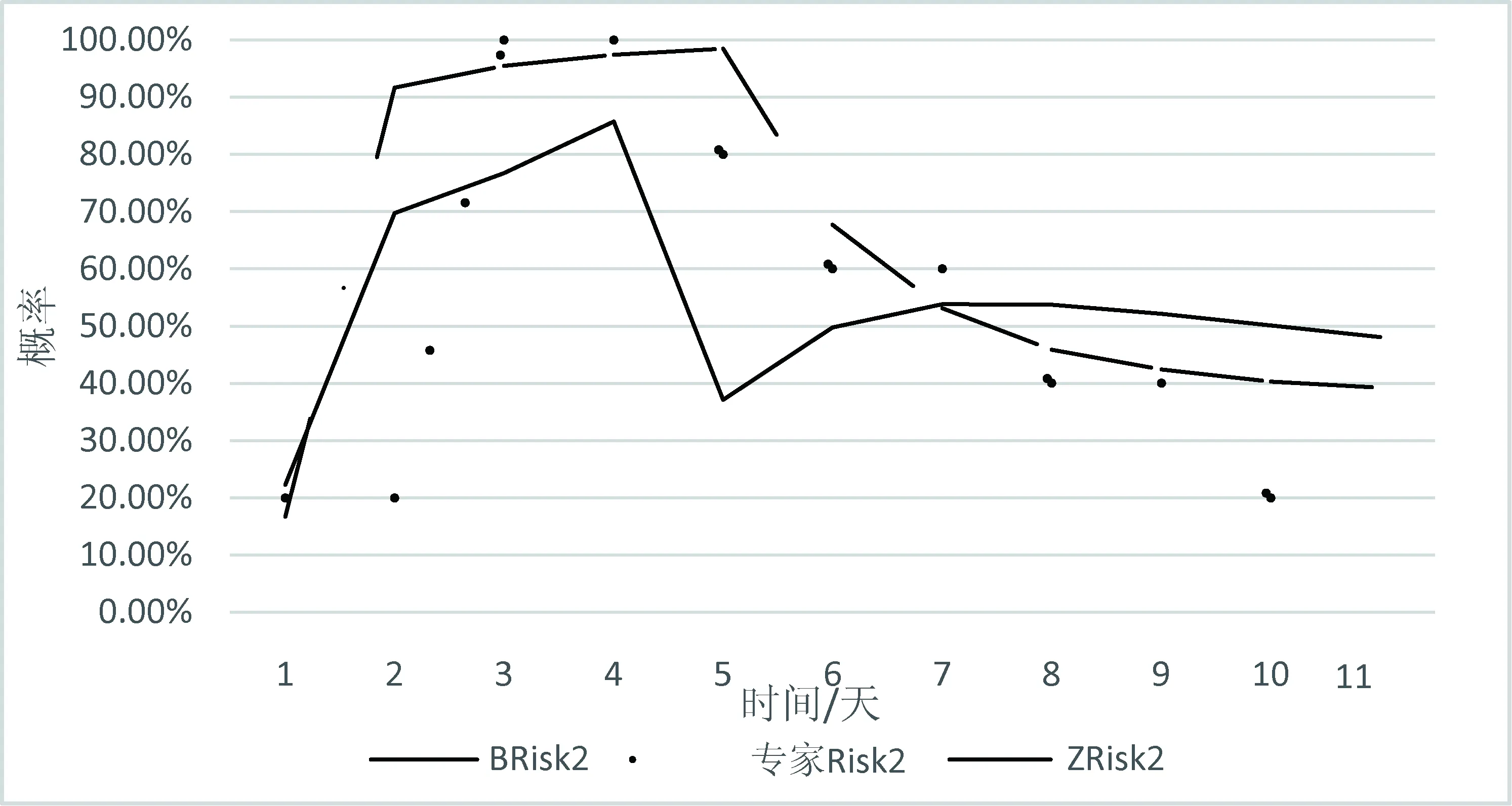
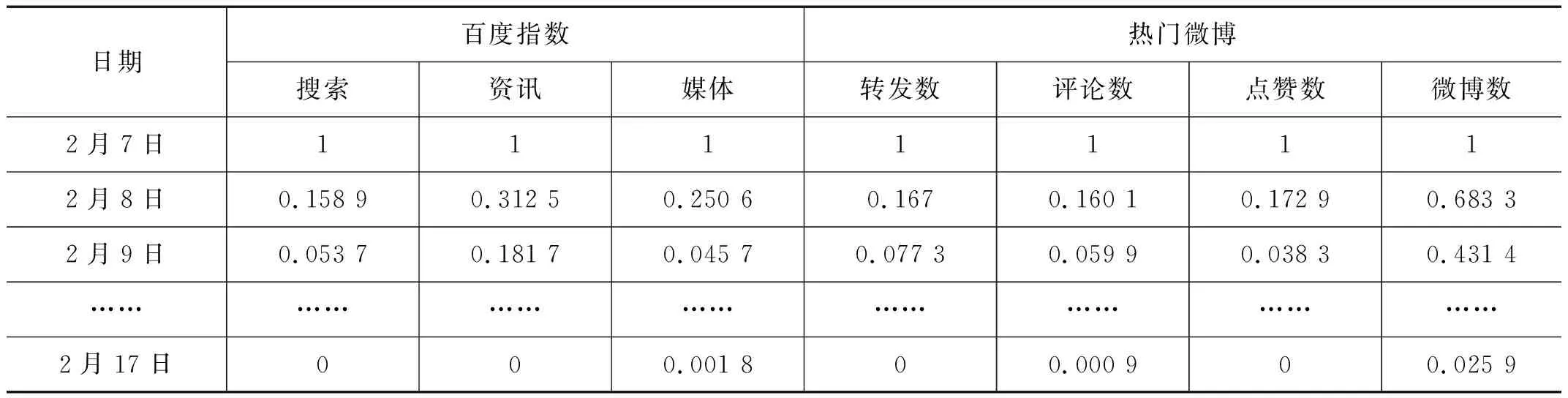
通過保留方差最大、包含原始數據最多的幾個主成分來實現高精度降維來實現保留了原始數據絕大部分信息的同時精簡數據集，本文選擇累計貢獻率>85%以上的r(r

λj對應的特征向量為Ej=(e1，e2，……，em)，(j=1，2，……，r)，以這些特征向量作列向量形成矩陣O=coeff(:,1:r)。

最終得到數據集B=O×X。最后用貝葉斯網絡算法對其進行預測。

2 實驗研究

2.1 網絡輿情數據采集與標準化處理

每個事件網絡輿情預測指標體系選取百度搜索指數、資訊指數、媒體指數、熱門微博數及微博轉發(fā)數、評論數、點贊數等7個指標，將獲取的XX房事件、李XX事件、鮑XX事件等6件網絡輿情事件的數據信息分為兩部分，其中李XX事件作為預測數據，其余數據做網絡輿情預測的樣本數據。本文將李XX事件作為演示案例數據來源，通過爬蟲對每項指標從2020年2月7日至2020年2月11日連續(xù)11天的信息采集。對已獲取數據進行標準化處理，本文采用Min-max標準化方法，將原始數據通過相關公式映射在[0,1]區(qū)間內。(標準化公式：[本數據-極小值/極大值-極小值])，標準化處理后數據如表1所示。

表1 標準化數據

2.2 降維

以每個指標在不同時間片的數據作為主成分分析訓練數據，這樣每個事件共有77個數據。用hij表示第i個指標在第j天的數據，構建出一個H=(hij)7*11的矩陣，對該矩陣進行主成分分析，可以得到李XX事件主成分貢獻率依次為為57.23%，21.75%，14.71%，4.94%，1.16%，0.11%，0.07%，故本實驗選取達到85%貢獻率的前3個主成分信息。通過信息計算得到：李XX事件前3個主成分分別能夠表達原始數據集93.17%，6.261%，0.367%的數據信息，即前3個主成分λ1，λ2和λ3可以解釋原始數據99.80%的信息量，因此，該數據集可以由8維降為3維。利用λ1，λ2和λ3的數據對網絡輿情進行分析，能夠達到精簡數據集的目的。最終得到數據Z如表2所示。

表2 主成分數據

2.3 建立貝葉斯網絡模型進行預測

2.3.1 確定網絡結構

本文使用Genie2.3軟件建立數據驅動的基于動態(tài)貝葉斯網絡的網絡輿情預測模型。采集數據指標共11天，所以網絡結構中建立共11步時間片。節(jié)點pca1，pca2和pca3即主成分數據λ1，λ2和λ3，其中節(jié)點pca1，pca2和pca3是節(jié)點Risk的父節(jié)點，節(jié)點pca3是節(jié)點pca2的父節(jié)點，節(jié)點pca2是節(jié)點pca1的父節(jié)點，同時節(jié)點pca1、節(jié)點pca2、節(jié)點pca3以及節(jié)點Risk均是下一個時間片上本節(jié)點的父節(jié)點，父節(jié)點與子節(jié)點存在因果關系，需要進行參數學習來得到先驗概率，構建貝葉斯網絡模型。

2.3.2 確定節(jié)點概率

本文選用5名專家意見對本事件11天期間內的Risk節(jié)點進行打分，Risk1代表輿情熱度降低，Risk2代表輿情熱度波動較小，Risk3代表輿情熱度升高。

2.3.3 數據離散化

由于主成分數據是連續(xù)值，而貝葉斯網絡的結構學習算法和參數學習算法要求各變量的輸入數據是離散值。因此，在結構學習和參數學習之前，需要預先對連續(xù)取值的數據進行離散化處理。

2.3.4 參數學習

建立動態(tài)貝葉斯網絡模型并確定其結構后，需要進行動態(tài)貝葉斯網絡參數學習，以獲取網絡中各節(jié)點隨時間的先驗概率分布。首先，建立一個數據量為1 000的隨機數據集進行參數學習，對先驗概率進行填充；然后，將XX房事件、鮑XX事件、XX連事件等5件輿情事件數據作為訓練集，將訓練集劃分為不同的時間片；最后，通過EM參數學習算法進行參數學習。

2.3.5 進行預測

參數學習確定貝葉斯網絡模型節(jié)點信息，將各節(jié)點的時序數據作為證據信息輸入到模型中進行預測，預測該事件網絡輿情風險狀態(tài)隨時間變化的概率。本實驗將李XX事件作為預測數據，輸入前5天的主成分數據基pca1，pca2和pca3，然后對網絡中各節(jié)點隨時間變化的后驗概率進行更新。

在當前輸入的證據信息下，得到突發(fā)事件網絡輿情風險節(jié)點的隨時間變化的概率預測結果。結果表明，在接下來的6天時間內，網絡輿情風險更大可能處于較小狀態(tài)(Risk1)，極小概率會達到較大(Risk2)或者重大(Risk3)的狀態(tài)。

根據預測結果繪制預測模型得到的輿情風險Risk1，Risk2和Risk3的概率值與輿情熱度趨勢實際值的對比圖，單純貝葉斯算法用Brisk表示，PCA-貝葉斯用ZRisk表示，預測結果對比如圖1—3所示。

圖1 Risk1預測結果對比

圖2 Risk2預測結果對比

圖3 Risk3預測結果對比

通過對比可得知，主成分分析貝葉斯算法要比單純使用貝葉斯算法對輿情進行預測的準確性更高，預測結果更接近實際情況。且在主成分分析算法進行濾過之后，貝葉斯算法的工作量大幅度減小。在指標數量巨大的時候效果尤為明顯。此方法可以為以后輿情方面的大數據工作提供幫助。目前，視頻網站發(fā)展迅猛，尤其是短視頻一直深受民眾歡迎。視頻中所表達出來關于民眾的意愿與觀點也尤為重要，希望該方法能夠在視頻輿情的研究中發(fā)揮作用。