日本落葉松以林分平均木材積生長率代替林分蓄積生長率可行性驗證

沈威

(遼寧省林業調查規劃監測院，遼寧 沈陽 110122)

研究用林分平均木的材積生長率代替林分蓄積生長率可能是未來的發展趨勢。林木材積生長率加入樹高因子，通過胸徑、樹高、年齡計算林木材積生長率將成為一種可能[1]。本文旨在研究利用日本落葉松材積生長率模型計算出小班平均木的材積生長率，代替林分蓄積生長率，林分蓄積乘以林分蓄積生長率計算出林分蓄積生長量，從而可預估林分未來幾年的林分蓄積[2-5]。

1 選取樣地

收集遼寧省森林資源連續清查1990年至2015年所有樣地信息，篩選出含有日本落葉松的固定樣地30個，使用EXCEL軟件中Vlookup函數查找相同樣地號的五個連查間隔期內同號木的檢尺類型、直徑值，組成列標題為樣地號、樣木號，6個檢尺類型、6個直徑的EXCEL表格。

2 計算林分蓄積生長率、林木材積生長率

選取5個間隔內，保留木齊全的固定樣地30個，查一元立木材積表計算每個固定樣地蓄積。計算樣地平均木材積。

利用普雷斯勒公式：

計算蓄積或材積的連年生長率。

式中：yt為本期蓄積或材積，yt-n為前期蓄積或材積，n為間隔期5 a。計算結果詳見表1。

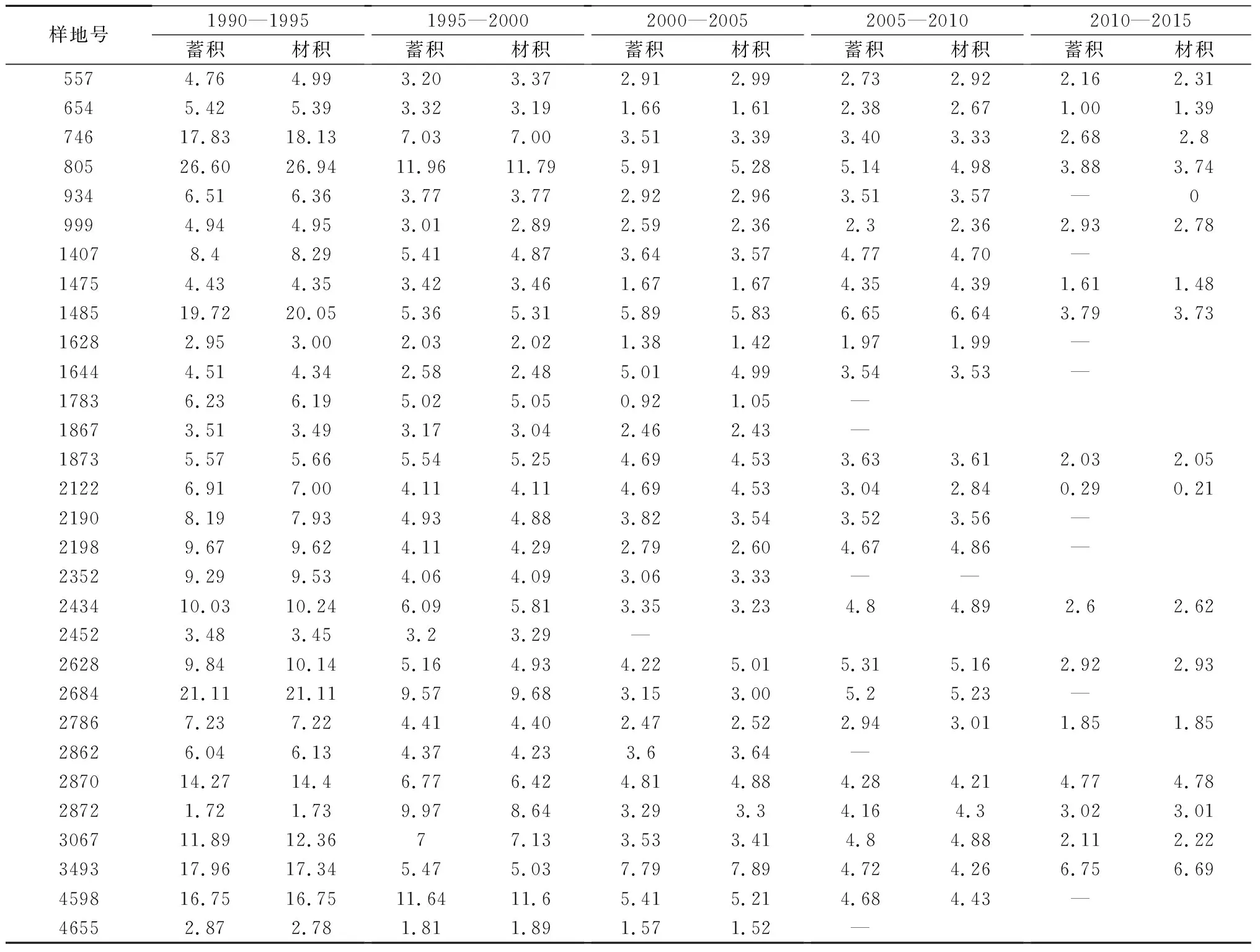
表1 日本落葉松材積和蓄積生長率

由表1可知，林分蓄積生長率和平均木的材積生長率比較接近，由此可以用林分平均木材積生長率代替林分蓄積生長率，把林分和林木緊密地聯系起來，研究林木材積生長率也就是研究林分蓄積生長率[6]。

3 適用性檢驗

為檢驗林分平均木材積生長率代替林分蓄積生長率的可能性，使用表1數據做檢驗樣本，檢驗方法用總相對誤差(RS)法和F檢驗[7]，當RS小于3%且大于-3%，同時通過F檢驗(F≤F0.05),則可以用林分平均木材積生長率代替林分蓄積生長率，否則不能代替。

3.1 總相對誤差

計算結果：RS=0.49%，大于-3%，小于3%。

3.2F檢驗

根據林分蓄積生長率yi和林分平均木材積生長率xi建立回歸直線方程yi=a+bxi，若林分蓄積生長率和林分平均木材積生長率無差異時，則直線截距a=0，斜距b=1，說明林分平均木材積生長率代替林分蓄積生長率適用。反之，則需在一定可靠性條件下，將點列回歸直線參數a、b與理想直線參數α=0，β=1進行差異性檢驗[8]。將檢驗相關數據代入方程式得回歸系數估計值。

直線參數的F值檢驗公式：

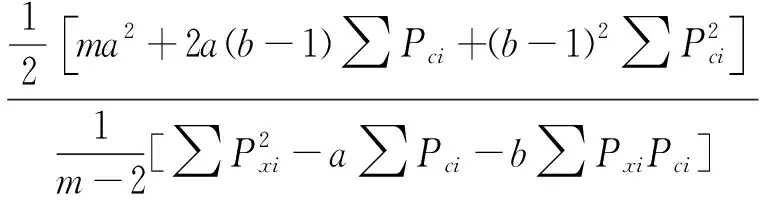
=1.34

式中m樣本個數，Pxi林分蓄積生長率，Pci林分平均木材積生長率 ，F服從自由度f1=2、f2=m-2-1的F分布。

當F>F0.05時，推翻假設，說明a不等于0，b不等于1，檢驗樣本實際值和估計值存在顯著差異，林分平均木生長率不能代替林分蓄積生長率。

當F≤F0.05時,說明a等于0，b等于1，檢驗樣本實際值和估計值沒有顯著差異，林分平均木生長率能代替林分蓄積生長率。

經計算得出F值，詳見表2。由表2可知F=1.34

表2 F檢驗值

4 結論

通過計算總相對誤差小于3%，F檢驗F≤F0.05，所以用林分平均木材積生長率代替林分蓄積生長率是可行的。把對林分蓄積生長率研究，轉移到對林分平均木材積生長率研究，解析林分平均木，就能研究胸徑生長率，樹高生長率，材積生長率。