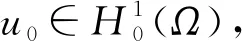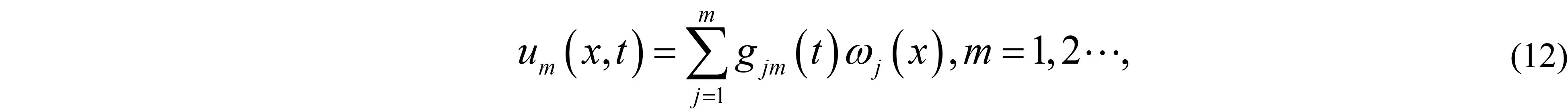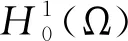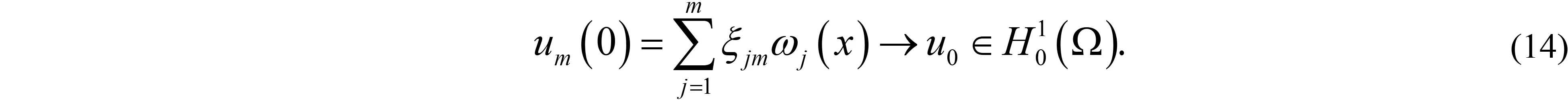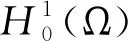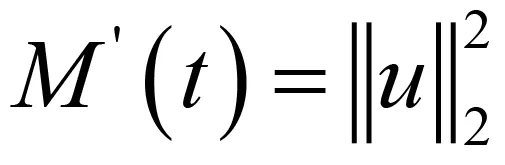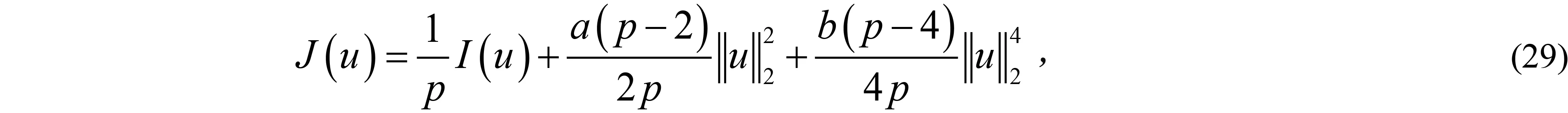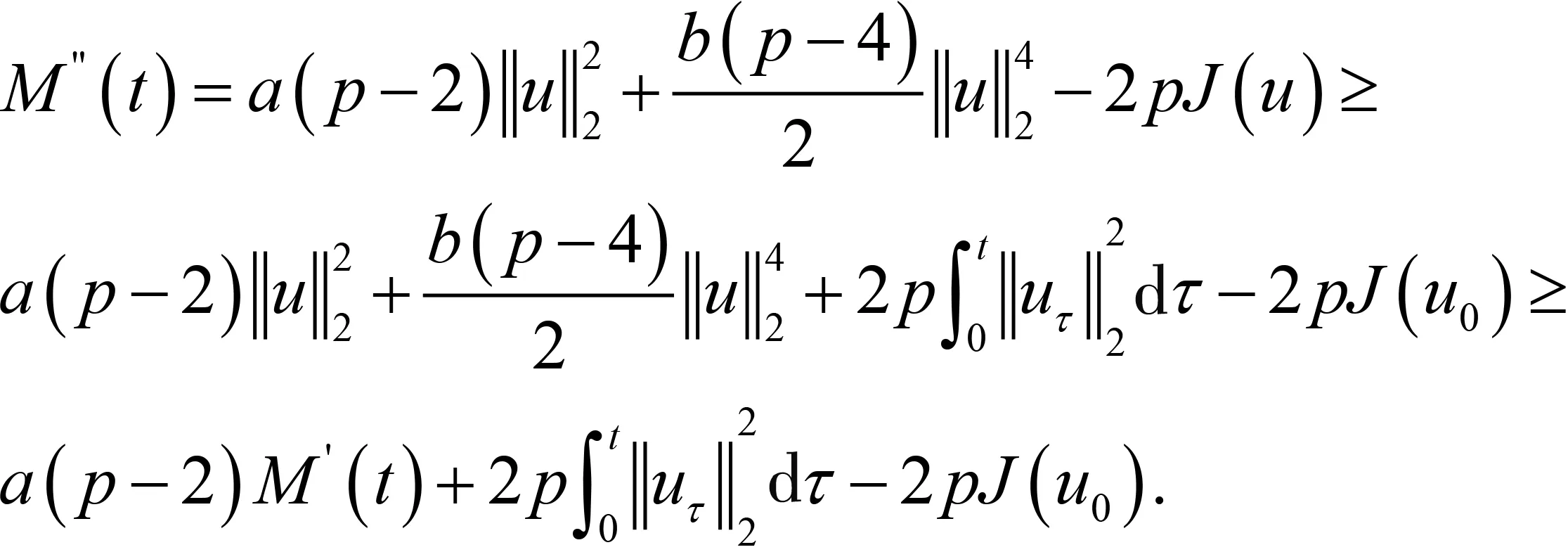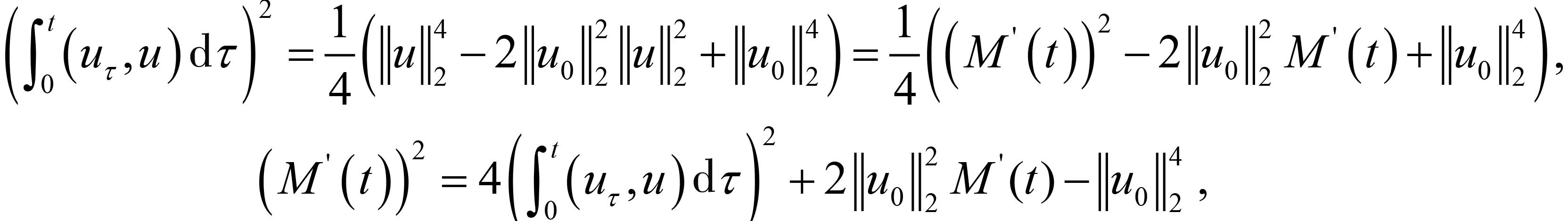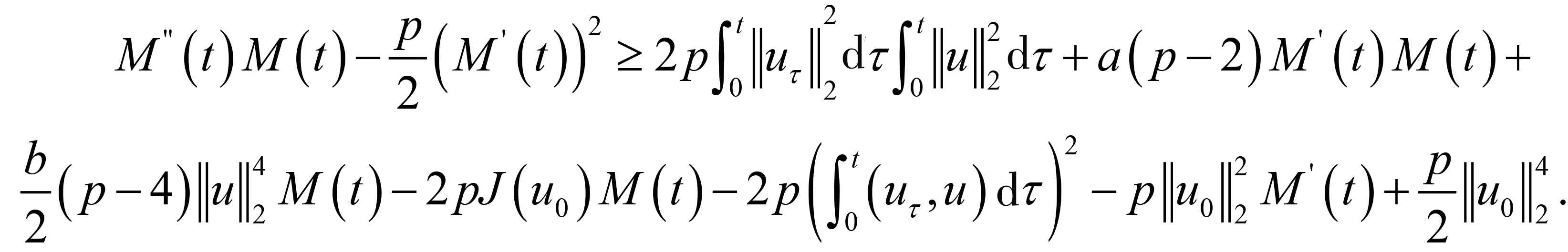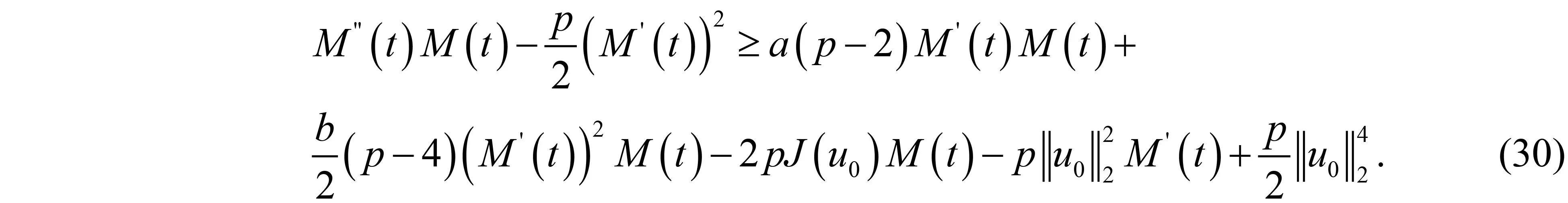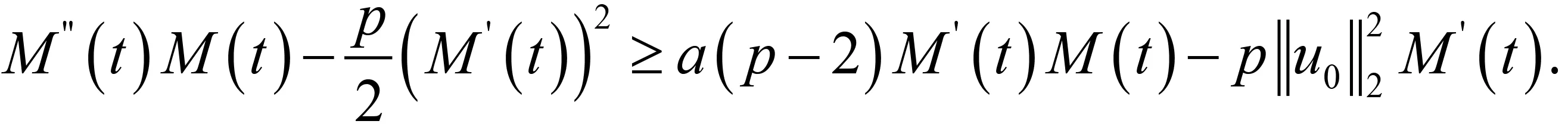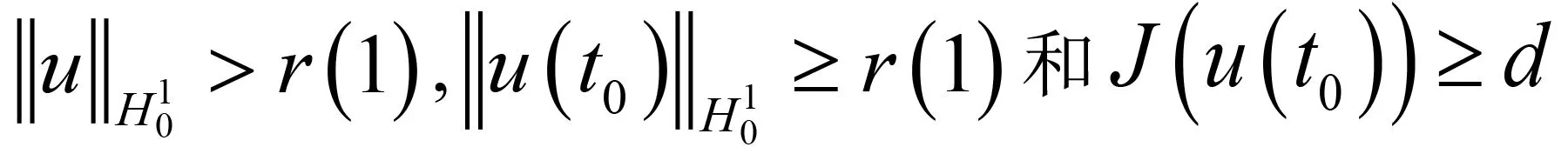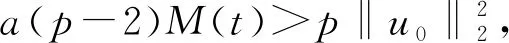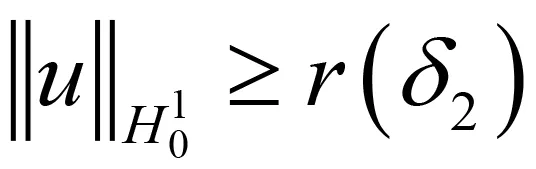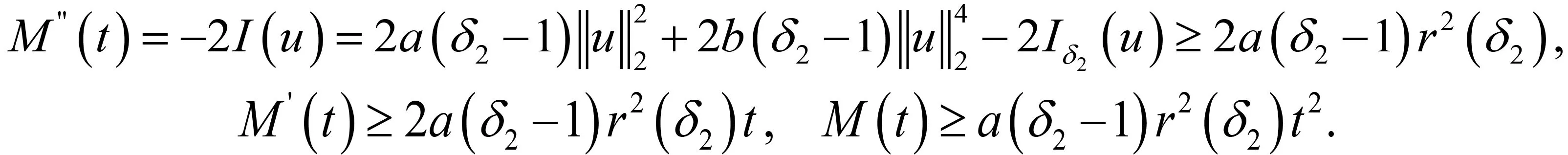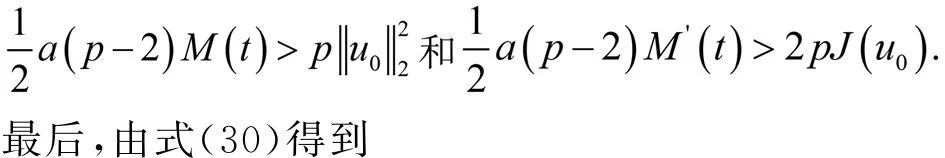一類基爾霍夫型非線性拋物方程解的存在和爆破
黃 瑤,石 鵬
(貴州民族大學 數(shù)據(jù)科學與信息工程學院,貴陽 550025)
0 引言
基爾霍夫(Kichhoff)方程在很多領(lǐng)域中都有廣泛應用,在利用數(shù)學方程建立物理模型的過程中總能找到相關(guān)的理論研究.在過去的幾十年里,學者們越來越關(guān)注基爾霍夫型問題的研究,基爾霍夫項經(jīng)常出現(xiàn)在雙曲線、橢圓型以及拋物線等不同類型的偏微分方程研究中[1-4].其中最原始的還是基爾霍夫本人在1883年提出的下列基爾霍夫模型:
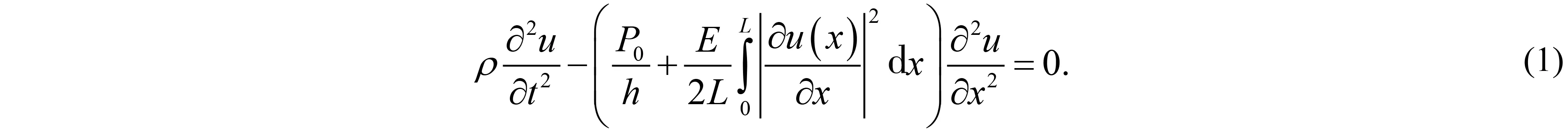
式(1)是著名的彈性弦自由振動的D’Alembert波動方程的推廣,其中:L為彈性弦的長度,h為橫截面積,ρ為質(zhì)量密度,P0為初始張力,E為楊氏模量.
近幾年,基爾霍夫方程在非線性偏微分方程的各項課題研究中十分活躍,在人口動力學、非牛頓力學、彈性理論等諸多領(lǐng)域方面,都能看到這類方程的廣泛應用.其中,2013年,Liu X和Sun Y[5]用Nehari流形的方法研究了一類基爾霍夫型微分方程兩個弱解的存在性.2014年,Liang、Li和Shi[6]利用拓撲度理論和變分方法研究了一類有漸近行為的基爾霍夫型微分方程正解的存在性.2018年,張申貴[7]利用臨界點理論研究了一類變指數(shù)基爾霍夫型方程的無窮多解.2019年,劉紫玉和韓偉利[8]用變分原理和山路引理證明了組合非線性項的基爾霍夫方程徑向解的存在性.
通常對非局部項做一定的改進,就可以得到一類新的方程.為了得到本研究中的一類基爾霍夫型非線性拋物方程,首先觀察下面這個含有基爾霍夫項的波動方程:
當α=0時,變成了一類含有基爾霍夫型的拋物方程:
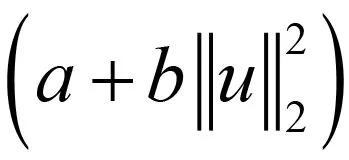
本研究對式(3)拋物方程賦予初邊值問題,得到下列一類基爾霍夫型非線性拋物方程:
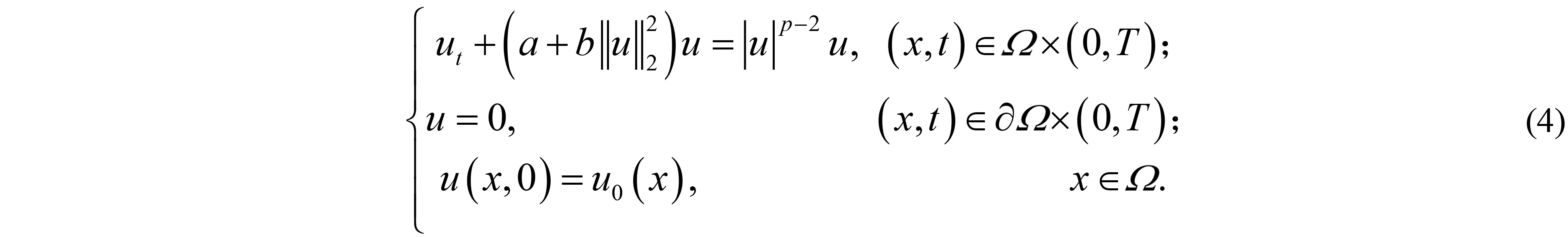
其中:Ω∈RN(N≥1)是具有光滑邊界?Ω的有界域,1 應用位勢井理論和變分法,可以研究當初始能量分別處于亞臨界、臨界和超臨界時解的整體存在性和有限時間爆破的結(jié)果,本研究著重討論亞臨界狀態(tài)J(u0) 為了更加方便地進行研究,首先引入位勢井,對于式(4),定義下列的能量泛函J(u)和Nehari泛函I(u),然后研究它們的功能和基本屬性. 定義Nehari流形 再分別定義位勢井和相應的集合如下: 引理2[10]假設u(x,t)是式(4)的弱解,0 1)如果I(u0)>0,則u(x,t)∈Wδ; 2)如果I(u0)<0,則u(x,t)∈Vδ. 其中,對于δ>0,可定義下面修改后的函數(shù)集合以及位勢井: 引理4[11]假設0 M″(t)M(t)-(1+γ)(M(t))2≥0,γ>0. 證明首先構(gòu)造式(4)的近似解為 和 因此,對于足夠大的m以及0 和I(um(0))>0成立. 這意味著對于足夠大的m來說um(0)∈W. 因此,由反證法證明了對于足夠大的m和t∈[0,T],有um(t)∈W. 由式(17),對于足夠大的m來說,有I(um(t))>0,則由式 及式(17),得到 上式對于足夠大的m和?t∈[0,T]均成立,且得到以下不等式 因此,由對角化知,存在一個u和{um}的子序列,使得 在式(13)中固定j,并令m=v→∞得到 和 由引理1和引理2,得到um(t)∈W.?0≤t<∞,這就證明了um(t)∈W. 由式(21)、(22)、(24)的收斂性,根據(jù)序列收斂原理以及式(5)中J(u)的定義,得出式(11)成立.因此,證明了極限函數(shù)u=u(x,t)是式(4)的弱解. 定理2假設a,b>0,1 證明令u為式(4)的弱解且滿足J(u0) 因為 如果p>4,由式(11)、(28)、(29)可以得到 因為 所以 利用Schwart不等式,得到 接下來,我們對如下兩種情況進行討論即可. 情形1:當J(u0)≤0時,則 現(xiàn)在證明?t>0,有I(u)<0.那么一定存在一個t0>0使得I(u(t0))=0和I(u(t))<0,其中0≤t
1定義和引理
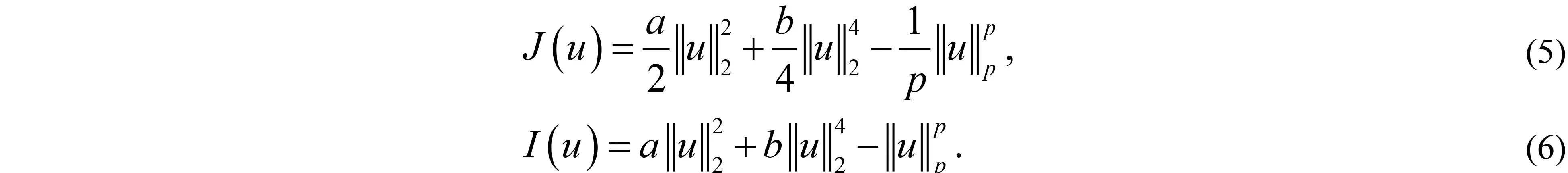
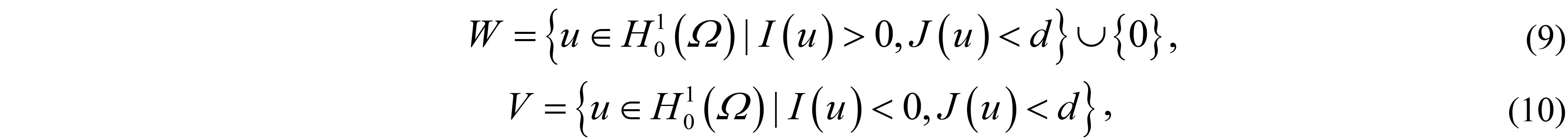
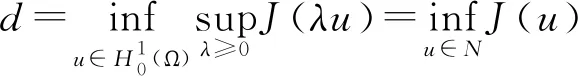
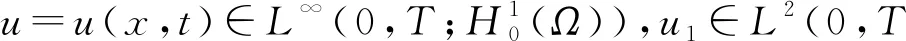
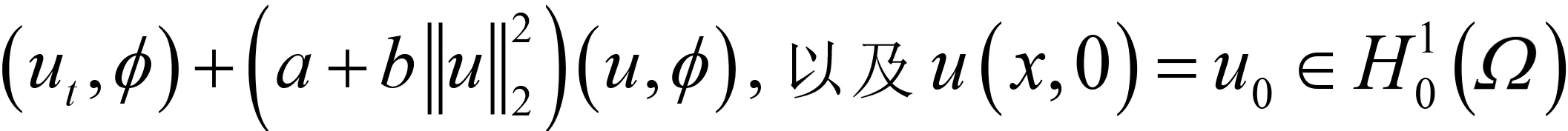
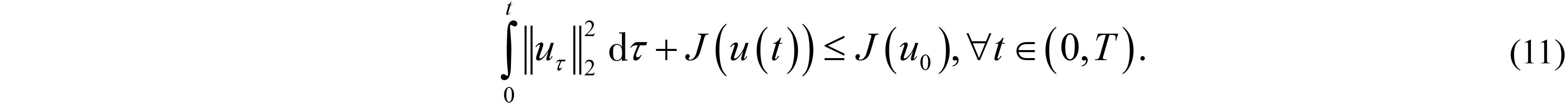
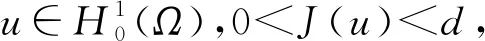
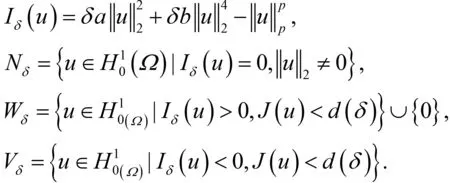
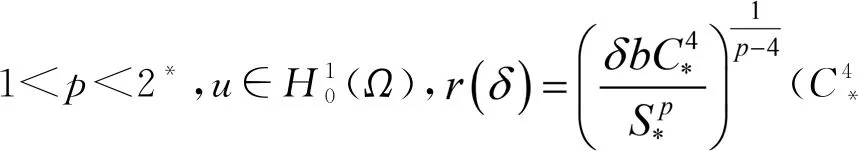
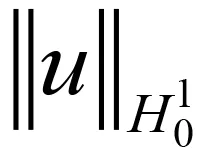
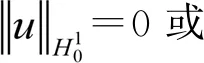
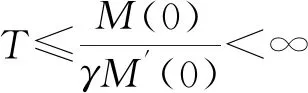
2 主要結(jié)果