如何在“追問”中讓學生的思維更加嚴謹

福建省福清市石竹中心小學 翁梅芳

一、在閱讀題目時追問，深入挖掘隱藏信息

理解題意是解決問題的前提，并且要收集解決問題所需的信息，弄清解決對象的特征，在頭腦中形成正確的問題表征，這些因素都有助于學生更好解決問題。由于小學生的閱讀能力、思維能力、知識基礎有限以及問題解決經驗的不足，導致學生對題意理解以及在問題內化上比較困難，對隱藏條件的發現就很困難了，而對于問題的深入理解更是難上加難了。因此，教學中，教師要鼓勵學生多讀幾遍題目，嘗試用自己的理解把題目的意思完整地表述。教師要引導學生善于捕捉并深入挖掘字里行間的隱藏信息，立足題目展開追問，在追問中展開思考，深入理解題意。

例如：在教學《植樹問題》時：同學們在全長1000 米的道路一邊植樹，每隔5 米栽一棵(兩端都栽)，一共需要多少棵樹苗？

師：邊讀邊想，從這個植樹要求中，你覺得哪些數學信息需要我們特別注意的？

生：每隔5 米很重要。

師追問：能說說每隔5 米的意思嗎？

生：也就第一棵樹到第二棵樹，第二棵數到第三棵數之間的距離都是5 米。(生邊說邊比劃)

師：這樣的距離數學上稱為“間距”（師邊比劃邊板書：間距）師：還有哪些要求呢？生：兩端都栽。

師追問：你覺得應怎么理解“兩端都栽”呢？

生1：就是路的頭和尾都要種。

生2：還要注意兩端指的是路的兩頭，兩邊指路的左右兩邊。

師：這是一個非常重要的信息。(板書：兩端都栽)

師：那這題目中還需要提醒大家的地方嗎？

生：在路的一邊植樹，只種一邊。

師：現在能完整說說你對題目的理解嗎？

學生再次解讀時準確強調了題意的重點。可見適當地追問題意的解讀可以培養學生的數學閱讀能力、數學思考能力。在追問中學生的理解由表層復述到深入剖析，由個人體會到全班共享，共同獲取了題中隱藏的信息，并且在深入理解題意的同時經歷了用數學語言表征問題的“數學化”過程。

二、在思維跳躍中追問，深刻理解知識聯系

《小學數學課程標準(2011 版)》指出:數學知識的教學，應引導學生進行觀察、分析，抽象概括，運用知識進行判斷，幫助學生理清相關知識之間的區別和聯系。在教學活動中，教師要直面學生的真實想法，耐心地解讀學生的思維活動情況，洞察學生思維的質與量，發展學生的思維能力。

例如：在教學四年級下冊《平均數》一課時，在“初步體驗平均數的特征”這一環節，前兩位同學3 次投球的平均成績分別是5 和4 的情況后，我是這樣引導的:

師：為了表示對壯壯(第三位投球同學)的友好，決定給他四次的投籃機會。

師：瞧，這是前3次的成績：3、7、5，你能很快地找到這3 次投籃的平均成績？(5 次)

師追問：用什么方法找到的？(移多補少、合并均分)

師：猜一猜，已經投完的兩位同學看到壯壯此時的投籃成績，可能會怎么想?

生：哇，要輸了。

師：從哪兒看出來的?

生：三次就投了15 個，已經和前兩人并列了，但他還有一次投球機會，肯定贏。

師面露疑惑追問：有沒有不同的想法？

遲疑片刻：不一定，萬一最后一次只投1 個或者沒投中，那肯定輸了。

師追問：說說理由。

生：因為前三次平均成績雖然是5，但最后一次如果只投中1 個，那四次的平均成績用移多補少法沒有球給補齊5 個了，所以他的四次投球的平均成績根本達不到5，所以輸了。(大部分學生若有所思開始點頭)

師追問：還有想說的嗎？

生：我覺得最后一次投出5 個就打成平手，投出6 個就贏定了。

師追問：為什么？

生：前三次平均成績已經是5 了。要想四次的平均成績達到5，那第四次必須投出5 個或5 個以上。(生鼓掌)

生：我發現這第四次投的個數會影響原來平均數。投比5 多，平均數就會比5 多；投比5 少，平均數就會比5 少；如果剛剛好投5 個，那平均數才不變。

師：真會思考，可見前3 個數據不變，第4 個數據變化，最后的平均數也跟著變化。其實一組數據的平均數它會隨著每一個數據的變化而變化，這是平均數的易變性特點。

師：你認為最終壯壯贏了還是輸了。

生：輸了，最后一次投得太少了。

師：不計算你能估計一下，壯壯最后平均成績可能是幾？(4 個)

師追問：瞧，第二次明明投中7個，為什么不估7 呢？

生：不可以，因為只有一次投了7 個，又不是次次都投中7 個。

生：7 個是投的最多的一次，要移一些補給少的，根本不會是7 個。

師質疑：那最后一次只投中1 個呀，為什么不估1 呢？

生：1 個是最少的，多的會補給他，這樣肯定就不止1 個。

E農1S是湖北省農業科學院糧食作物研究所以廣占 63－4S［1］為受體、以抗稻瘟病品種 GD－7［2］為供體，通過雜交、回交和自交，結合分子標記輔助選擇技術選育的攜帶抗稻瘟病基因Pi1和Pi2的兩系不育系。2016年通過湖北省農作物品種審定委員會審定，品種審定編號為鄂審稻2016028。以E農1S為母本配制的雜交組合目前已有E兩優476［3］、E兩優186［4］和E兩優222通過了品種審定。

師：這樣看來盡管最后成績還沒算出來，但我們可以肯定最后平均數會是什么情況？

生：應該是比這一組數里最大的數小，還要比最小的數大一些。

師總結：平均數介于最大數和最小數之間，這也是平均數的一個特點。

面對教師巧妙地追問，通過猜一猜、估一估，學生對平均數以及平均數取值范圍有了感性深刻地認知，進一步溝通了平均數與具體數據的聯系。可見，課堂中適時加以追問，引導討論交流，培養了他們互相借鑒、互相補充的能力。從而進一步理解知識之間的聯系，充分發展了學生的數據分析能力、推理能力以及創新意識。適時地追問激發了學生表達的欲望，延伸了知識的空間，感悟了數學的魅力，獲得了成功的體驗，真正讓學生的思維走向豐富走向深度。

三、在錯誤理解中追問，深度把握知識本質

由于學生在對問題理解中出現錯誤是正常的，這些錯誤單靠教師反復強調是不能從根本解決問題的。需要學生經過“自我否定”的過程，就是需要在一個“觀念沖突”的情境中自然產生。

例如：在教學三年級上冊《數學廣角——集合》時：學校將舉行三年段跳繩比賽和踢毽子比賽。要求:每個班選8 名同學參加跳繩比賽，7 名同學參加踢毽子比賽。

師：根據信息你會提什么數學問題？

生：每個班一共多少人參加這兩項比賽？

師：你認為每班一共多少人參加呢？(15 人)

師追問：怎么想的？

生：8+7=15 人。

師：有沒有不同意見?(沒有)

師：那是不是一定得有15 人呢？(是)

師：看301 班選出的參賽名單出示原始數據，發現問題。

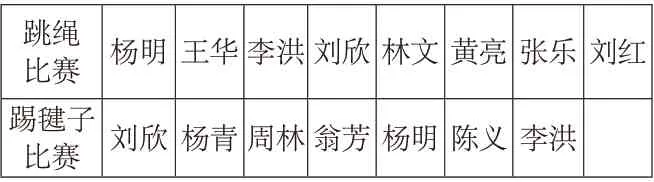
跳繩比賽 楊明 王華李洪劉欣 林文 黃亮 張樂 劉紅踢毽子比賽 劉欣 楊青周林翁芳 楊明 陳義 李洪

師質疑：301 班真有15 人參加比賽嗎？請仔細觀察這份參賽名單，你有什么發現？

生1：我發現楊明、劉欣兩項比賽都參加。

生2：李洪也是。

師追問：現在你們還認為301 班有15人參加比賽嗎？(沒有)說說理由。

生：跳繩比賽中有楊明、劉欣、李洪，踢毽子比賽中也有他們3 個，15 人中這3 個人重復算了，應該減掉3 人。(都點頭贊同)

師：可這份名單我們能一下子看出哪些同學重復參賽嗎？(不能，有點亂。)

師：請你們想想辦法，怎樣整理能夠讓人很容易看出哪些人兩項比賽都參加。(學生開始積極主動合作探究解決法案)

此時，教師直面學生的問題，通過設置懸念使學生產生疑惑，這么簡單的問題，怎么可能出現錯誤呢？緊接著出現班級學生參賽數據，通過追問使學生明白了產生問題的原因，即出現重復現象。充分地暴露學生思維過程，這一過程教師及時把握，因勢利導，適時追問，促進學生主動探究，自我否定，自我修正，從而探索最優方法便成了學生內心的學習需求，并在這個過程經歷了知識的形成，把握了知識本質。

總之，在課堂教學中，適時有效地追問，可以提高學生數學學習的實效性。