基于動力吸振器的艦炮徑筒減振分析

富 威，吳 瓊，趙書樊，龔軍軍，徐蕓潔，王美娟

(哈爾濱工程大學 機電工程學院， 哈爾濱 150001)

艦炮是海軍水面艦艇上的傳統武器，在數次海戰中都發揮著極大的作用，當代的國防發展中，艦炮武器更是不可缺少的一部分。艦炮具有自動化程度高、對來襲的目標反應靈活、攻擊覆蓋面大、持續發射和精確度高等優點，現代的作戰平臺要求艦炮武器具有功能多樣化，打擊精確化，武器輕型化，機動作戰快速化，指揮控制及平臺信息化等特點。在艦炮連續發射的情況下，產生的振動沖擊會更加強烈。這種沖擊載荷和強烈振動會對艦炮結構造成一定的破壞，影響其穩定性，并且會使其使用壽命縮短。因此，通過對艦炮典型部件的振動特性分析，并對其設置減振系統，是發展和完善我國艦炮的亟需解決的問題。

隨著高速傅里葉變換器和在此基礎上試驗模態分析技術的出現，動力吸振器迎來了一個新的時代。李新興等[1]分析了吸振原理，重新推導了傳統吸振器的優化公式；宋孔杰等[2]對動力吸振器進行了優化設計，主要考慮了吸振器在不同的振動源的作用下的影響；張洪田等[3]設計了一種電磁式吸振器，并且將其應用在船舶用發動機上；鄧華夏等[4]用磁流變彈性體替代傳統的動力吸振器的彈性體，并且將新型的動力吸振器用移頻調諧的方法進行控制，得到了一種更加靈活可靠以及能夠調頻的動力吸振器。張琳[5]基于動柔度方法中的被動修改法,推導得出附加彈簧質量系統的多自由度系統的動柔度矩陣,并對該多自由度系統中的目標自由度進行零點配置,使該自由度下的相應振動得到抑制。賈富淳[6]為了提升參數型動力吸振器的吸振效果,文中提出一種用于控制桿縱向模態振動的連續參數型懸臂梁動力吸振器。郎軍[7]將半主動開關型控制策略應用到接地式動力吸振器中,并進行性能分析和參數優化.首先,利用平均法求得兩種半主動接地式動力吸振器的近似解析解,并與相應數值解對比,驗證了解析解的正確性與高精度.然后,對兩種半主動控制接地式動力吸振器進行參數優化。賀輝雄[8]針對動力吸振器在船舶領域應用較少及艦艇在低頻振動時減振降噪措施較難實現這一現狀,構建低頻線譜激勵下艦艇附加動力吸振器設計流程及研究其減振降噪特性。江雄以[9]器件上最大加速度響應有效值最小化為減振設計目標,以吸振器安裝位置、尺寸等參數為設計變量,對吸振器進行優化設計,比較了不同材料、不同形式吸振器的減振效果。邢昭陽[10]以Voigt型動力吸振器為基礎提出了一種將放大機構應用于含負剛度彈簧元件的動力吸振器模型,對該模型的最優參數進行了研究。蘇智偉[11]針對艦船大型機械設備振動沖擊隔離對高傳遞損失減振抗沖元器件的需求,基于負剛度動力吸振機理,構建一種含負剛度(NS)元件的動力吸振器(DVA)混合隔振系統。李強[12]為有效抑制航天設備中由干擾源誘發的低頻/超低頻振動,提出了一種新型可調動力吸振器(NDVA)。該動力吸振器主要由柔性螺旋彈簧(SFS)及磁性負剛度彈簧(MNSS)組成。付江華[13]設計了動力吸振器多參數優化目標函數,研究人群搜索算法在動力吸振器參數優化中的應用,并運用人群搜索算法、遺傳算法和粒子群算法進行仿真計算,對比3種算法對動力吸振器進行參數優化時的穩定性、計算速度、計算精度。王衛峰[14]針對某一特定頻率下的振動問題,優化了有阻尼吸振器參數來對其進行吸振。

動力吸振器的設計過程趨于成熟，但是吸振器的參數優化，例如吸振器質量的尋優還沒有深入的研究。本文通過研究搖架徑筒的受迫振動特性、編寫Matlab程序，實現吸振器質量的尋優過程。

1 徑筒振動特性分析

對如圖1所示的等截面徑筒進行分析，忽略其他架體結構的影響，但整體質量不能忽略，在懸臂梁的固定端添加一個集中質量，根據所選目標的實際質量，添加了5 000 kg的集中質量。

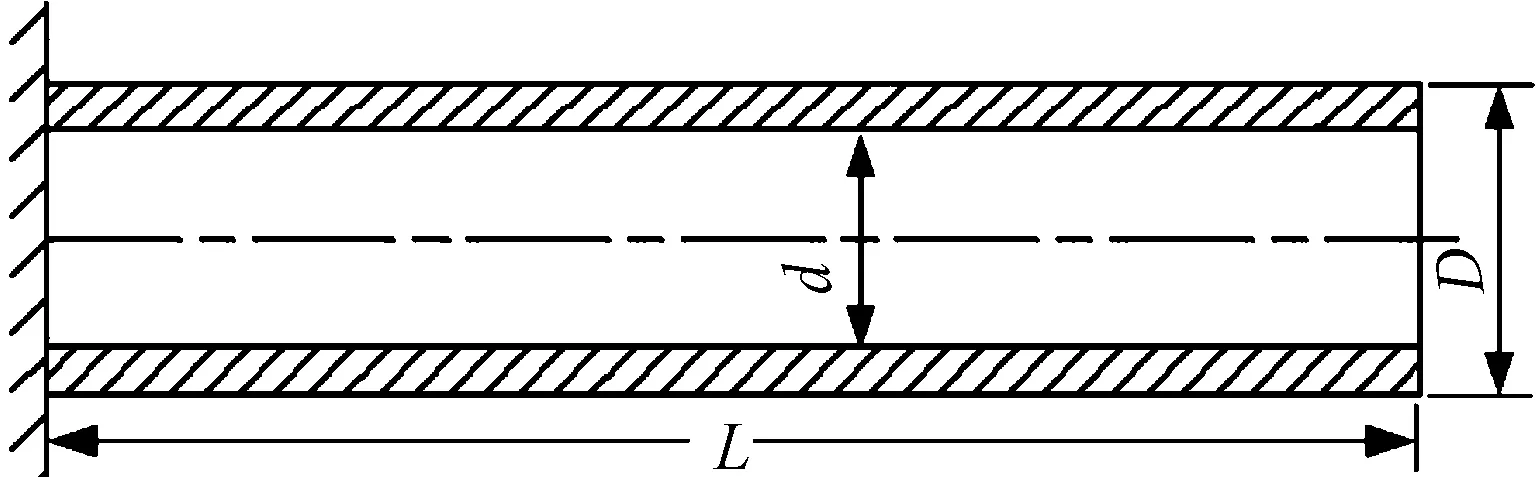
圖1 徑筒結構簡圖

徑筒結構簡化的參數如表1所示。

表1 徑筒參數表

1) 徑筒橫向自由振動方程

根據徑筒的簡化模型，其橫向振動方程可以寫為：

(1)

式中：A為徑筒的橫截面積；E為徑筒材料的彈性模量；ρ為密度，徑筒的材料均勻，在整個模型中E和ρ為常量，I為徑筒的截面慣性矩。假定整個系統具有同頻諧振動，則徑筒的一般橫向振動方程為：

y(x,t)=φ(x)sin(ωt)

(2)

式中：φ(x)表示徑筒的振型函數；ω為徑筒的圓頻率。

整理得到：

(3)

對式(3)進行求解并求導得到：

φ′(x)=C1kcos(kx)-C2ksin(kx)+

C3kch(kx)+C4ksh(kx)

φ″(x)=-C1k2sin(kx)-C2k2cos(kx)+

C3k2sh(kx)+C4k2ch(kx)

φ?(x)=-C1k3cos(kx)+C2k3sin(kx)+

C3k3ch(kx)+C4k3sh(kx)

(4)

將式(4)中的x用搖架徑筒的長度L替換，由于搖架徑筒簡化為懸臂梁，所以左邊的邊界條件為撓度y(0)和轉角θ(0)為0，另一邊的邊界條件為彎矩M(L)和剪力Q(L)為0，整理可以得到懸臂梁兩個端點的關系式為:

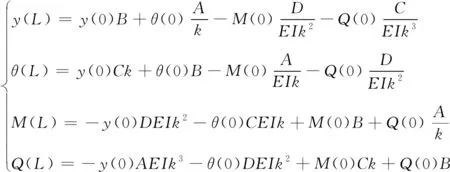
(5)

設：

將邊界條件代入式(5)并進行整理，可以得到：

(6)

若使式(6)具有非零解，那么可以推導出：

ch(kL)·cos(kL)+1=0

(7)

此方程是懸臂梁的頻率方程，能夠解出kL的值，前三階的值為：k1L=1.875，k2L=4.694，k3L=7.855。搖架徑筒的參數為：密度ρ為7 850 kg/m3，彈性模量E為2.1×1011Pa，將k1L的值代回可以得到懸臂梁的一階橫向振動方程。

2) 徑筒的橫向受迫振動方程

設φ(x)為搖架徑筒的橫向振動振型函數，則搖架徑筒的動能和勢能的表達式為：

(8)

式中qi為廣義坐標。

在艦炮發射時，搖架受到身管傳遞過來的載荷，因為這里只分析搖架的徑筒，搖架徑筒所受到的激勵為：幅值為100 000 N，頻率為5 Hz，即：

F(t)=100 000sin(10πt)

(9)

在搖架徑筒位置的橫向位移響應可表示為可表示為：

y(x,t)=∑iφi(x)qi(t)

(10)

由虛位移原理推導得到廣義力表達式為：

(11)

Lagrange方程為：

(12)

聯立式(8)、式(12)，在系統不同的廣義坐標下進行求解，得到：

(13)

廣義質量與廣義剛度的表達式為：

(14)

由式(12)、式(13)以及式(14)可以得到運動微分方程，寫成矩陣形式為：

(15)

可以寫成：

(16)

編寫MATLAB程序，得到搖架徑筒上各點的響應，并且使用ANSYS/Mechaincal APDL軟件，用有限元法再次計算搖架徑筒上各點的響應，理論計算值與有限元法計算結果如圖2所示。

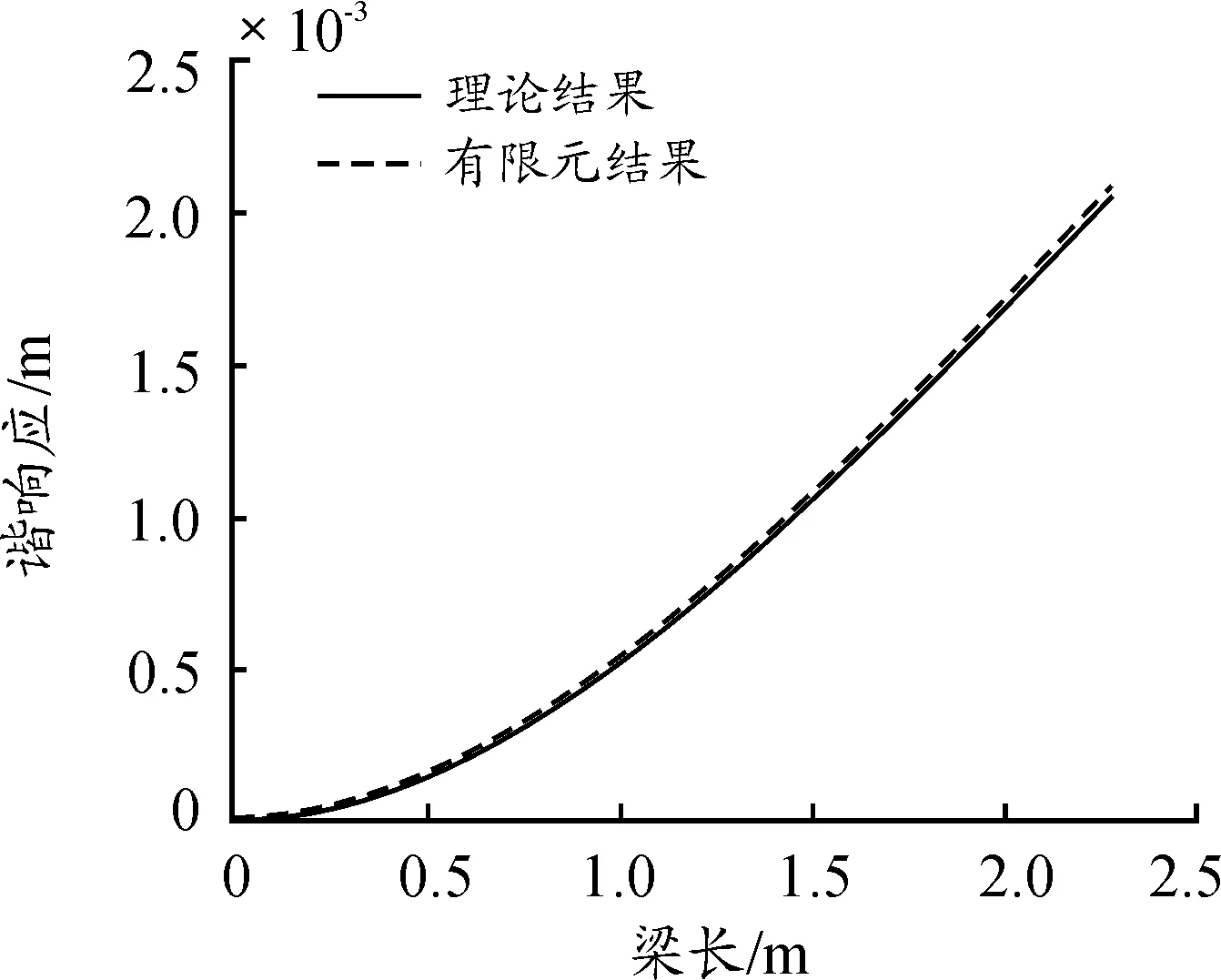
圖2 徑筒上各點的響應曲線

根據圖2所示，當搖架徑筒上不加吸振器時，由理論計算得到的結果與有限元分析結果基本一致，證明利用振動方程求出動能和勢能后代入第二拉格朗日方程求解不加吸振器時搖架徑筒上各點的響應的方法是正確的。

2 帶有吸振器的徑筒振動特性分析

本文選用被動式吸振器，具有較高的精度，相比于其他的動力吸振器，被動式吸振器具有結構簡單，吸振性能穩定等特點，降低了生產成本。在徑筒上安裝一個被動式吸振器來使其振動減小，其中mx-kx-cx組成的系統為吸振器的理論結構，結構簡圖如圖3。

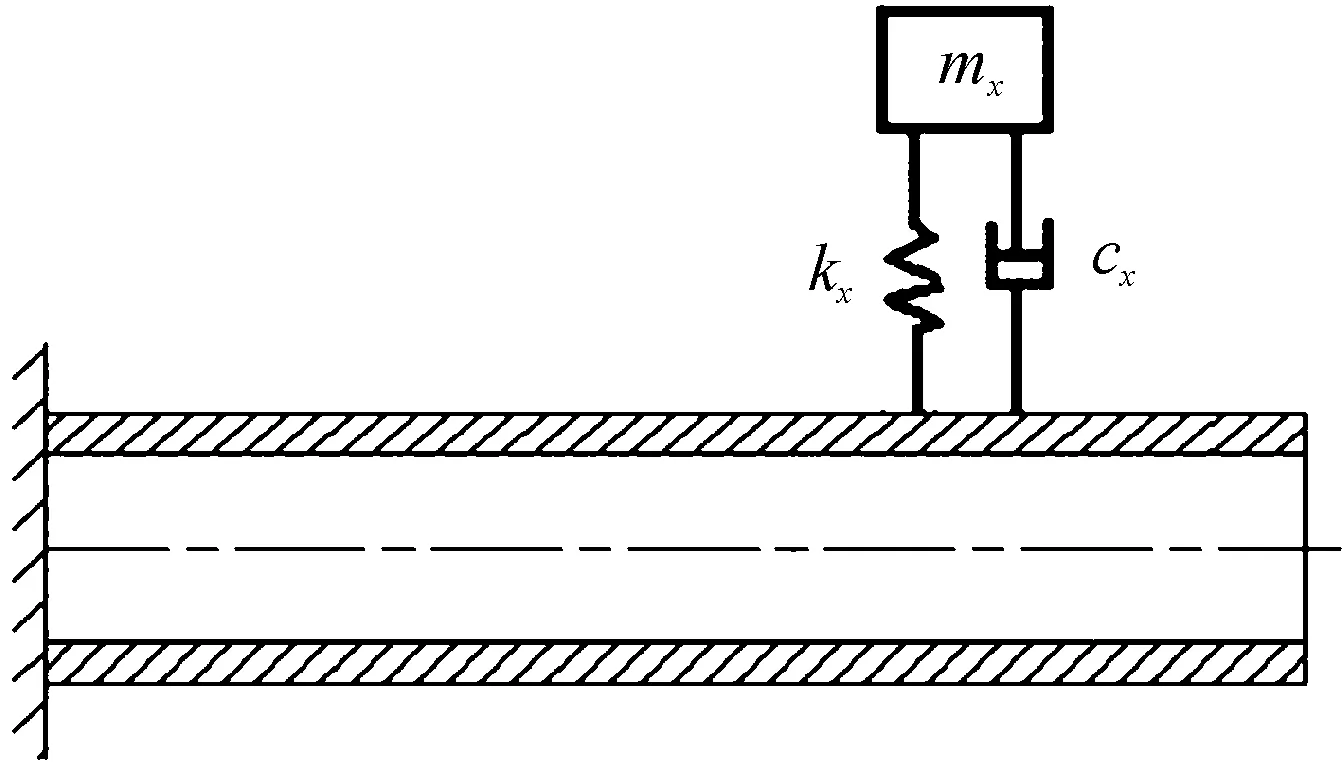
圖3 帶有吸振器的徑筒結構簡圖

設x0為吸振器在徑筒上的安裝位置，mx表示吸振器的總質量，kx表示吸振器的剛度，ξ表示吸振器的位移，cx表示吸振器的阻尼。將吸振器安裝在徑筒上后的系統的動能和勢能表達式為：

(17)

將式(17)代入到第二拉格朗日方程中，可以得到：

(18)

(19)

加入吸振器后廣義質量和廣義剛度的表達式為：

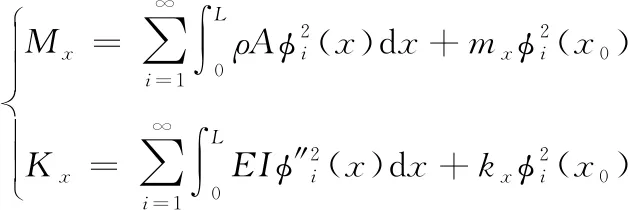
(20)

使用模態疊加法，設目標部件的響應求解位置為LR，可以求解該位置的受迫響應為：

(21)

將吸振器的質量設置為1 kg，編寫相應的MATLAB程序，安裝在徑筒的自由端，求出帶有吸振器的徑筒上的各點響應，同時，使用ANSYS/Mechaincal APDL軟件，用有限元法求解加入吸振器后徑筒的響應與計算理論結果如圖4所示。

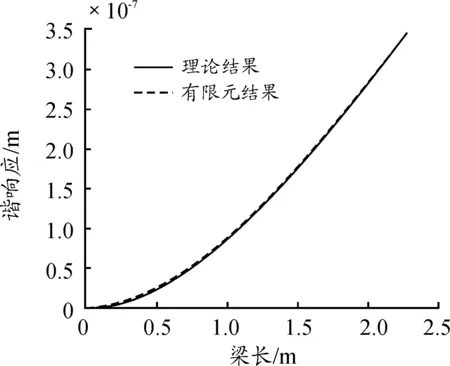
圖4 帶有吸振器的徑筒上各點的響應曲線

根據圖4所示，當徑筒上安裝吸振器時，理論計算得到的結果與有限元分析結果基本一致，證明利用振動方程求出動能和勢能，然后將其代入第二拉格朗日方程求解安裝吸振器的徑筒上各點的響應的方法是正確的。

3 動力吸振器優化設計

動力吸振器的設計受多方面的制約，改變某一個參數時，對動力吸振器的吸振效果都會產生很大的影響。動力吸振器性能的好壞受到在待減振系統中的吸振器的阻尼/吸振器的質量比的影響。為了將吸振器的性能達到最優，設計人員在進行動力吸振器的設計時，必須要考慮質量方面的作用。

動力吸振器的吸振效果的好壞與吸振器的質量有關，因此在本節中對吸振器的質量進行尋優。在徑筒上安裝動力吸振器，動力吸振器的安裝位置保持不變。設置吸振器的剛度為986.96 N/m，設動力吸振器的形式為粘性阻尼，設置阻尼比大小為0.002。

動力吸振器質量的不同會直接導致響應情況的不同。計算在徑筒受到幅值大小為100 000 N，頻率為5 Hz外界激振力作用時的受迫響應。將動力吸振器的安裝位置保持不變，改變動力吸振器的質量，分析徑筒自由端的響應情況。利用Matlab軟件編寫將吸振器安裝在自由端時，質量尋優的程序。

經過計算得到動力吸振器質量不同時徑筒自由端的響應曲線如圖5所示。

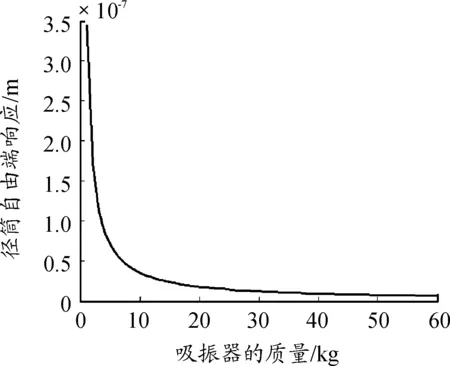
圖5 動力吸振器質量不同時徑筒自由端的響應曲線

通過圖5可以看出，動力吸振器的質量對吸振器的吸振效果有很大的影響。當保持吸振器的安裝位置不變時，隨著吸振器質量的增大，徑筒自由端的振動幅值越小。當吸振器的質量在0～10 kg時，隨著質量的增大，徑筒自由端的振動幅值迅速變小；當動力吸振器的質量大于等于15 kg時，徑筒自由端的振動幅值減小的幅度不在那么明顯。綜合上述分析可以得到：動力吸振器的質量雖然能夠對吸振效果影響明顯，但是吸振器的質量不是越大越好，當吸振器的質量達到一定數值時，吸振器的效果不在那么明顯。因此合理選擇動力吸振器的質量，不但可以達到對徑筒減振的效果，還會減輕徑筒的整體質量，減少動力吸振器的制造成本。

從圖6可以看出，動力吸振器的質量一定時，徑筒上各處位置越靠近炮筒的自由端，振動幅值越大。動力吸振器的質量在大于等于15 kg時，徑筒上各點的振動幅值基本相同。因此可以得出相同的結論：在動力吸振器的質量不是越大越好，合理選擇動力吸振器的質量，不但可以達到對徑筒減振的效果，還會減輕徑筒的整體質量，減少動力吸振器的制造成本。

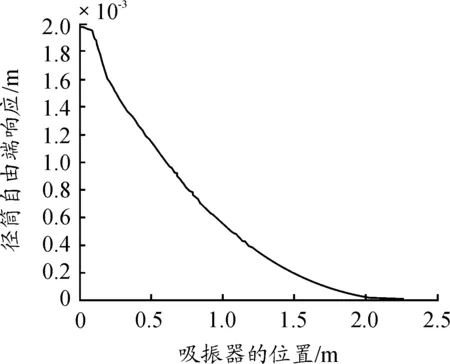
圖6 動力吸振器安裝位置不同時徑筒自由端響應曲線

綜上所述，動力吸振器應該安裝在徑筒的自由端，質量為15 kg，剛度為14 804.4 N/m，阻尼比大小為0.002，此時，吸振效果達到最好。

4 結論

本文分析了動力吸振器的影響因素，對動力吸振器的安裝位置和質量進行優化設計，了解安裝位置和質量對動力吸振器吸振效果影響的規律：在動力吸振器的安裝位置不影響徑筒正常運作的前提下，動力吸振器的安裝位置越靠近徑筒的自由端，吸振效果越好；動力吸振器質量增大，徑筒自由端的振動幅值減小，但動力吸振器的質量不是越大越好，合理選擇動力吸振器的質量，可對徑筒減振，減少動力吸振器的制造成本。