彈道修正引信隔轉平臺抗高過載優化設計

李鑫鵬，郭朝勇，孔剛鵬，周煊博，惠江海，張華平

(1.中國華陰兵器試驗中心， 陜西 華陰 714200；2.陸軍工程大學石家莊校區 車輛與電氣工程系， 石家莊 050003)

現代戰爭對陸軍炮兵武器裝備的作戰效能、反應時間、低附帶毀傷、低成本打擊等多個方面提出了越來越高的要求，傳統的大規模壓制作戰越來越難以實施，精確壓制和精確打擊已經成為炮兵追求的主要目標[1-2]。精確制導彈藥成本過高，不能大量裝備部隊，為了有效解決不斷提高的精確打擊需求與不斷增長的彈藥生產成本之間的矛盾，彈道修正引信應運而生[3-5]。國外對彈道修正引信的研究已取得一定成果，如美國的CCF、CMATD、PGK，英國的“斯塔爾”，以色列的CTAP等[6-9]。國內相關單位對彈道修正引信也有一定的研究，但尚無型號產品出現[10-12]。

彈道修正引信進行彈道修正時，需要修正舵機能夠以不同于彈體的轉速而轉動。但是，受外形尺寸以及結構空間的限制，在炮彈高過載發射環境下，彈道修正引信中的隔轉件極易造成破壞，導致修正舵機相對彈體無法正常轉動[13]。

針對上述問題，本文以提高隔轉件的抗過載能力為目的，從優化隔轉件的結構和參數出發，采用滿裝球支撐方式優化設計了彈道修正引信隔轉平臺，基于Hertz接觸理論和動靜耦合的有限元仿真方法分析優化了隔轉平臺的結構參數，獲得了能夠滿足屈服強度要求的隔轉平臺優化方案。

1 隔轉平臺設計

隔轉平臺既要實現彈道修正引信修正舵機與彈體的旋轉隔離，滿足彈道修正時所需的功能要求，又要適應炮彈惡劣的發射環境，保證自身結構的強度要求。根據已有研究，彈道修正引信中隔轉件的失效主要體現為隔轉件中滾珠與滾道的過載損壞[14]。因此本節從優化隔轉件結構出發，采用滿裝球支撐方式設計了隔轉平臺。

1.1 滿裝球支撐原則

滿裝球支撐即在滾道參數一定的條件下，去除支撐滾珠的保持架，并以最大數量的滾珠裝滿于滾道之間，通過滾珠之間的接觸支撐防止滾珠出現旋轉游動現象，以保證滾珠的支撐剛度。滿裝球支撐示意圖如圖1所示。為了保證滾珠的順利安裝，在內外圈上設計了安裝槽，通過改變內外圈安裝槽的相對位置，保證滾珠的順利安裝，并防止滾珠工作時的外漏。滾珠安裝時，內外圈安裝槽對齊，如圖2所示。滾珠工作時，內外圈安裝槽錯開，如圖3所示。

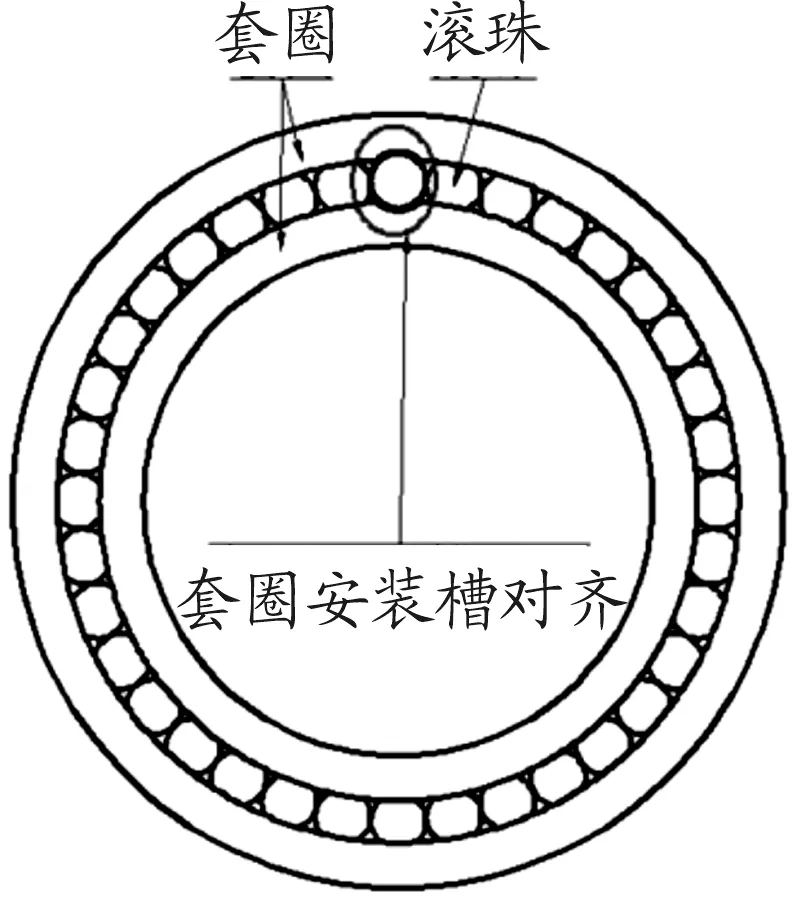
圖2 滾珠安裝時安裝槽位置關系示意圖

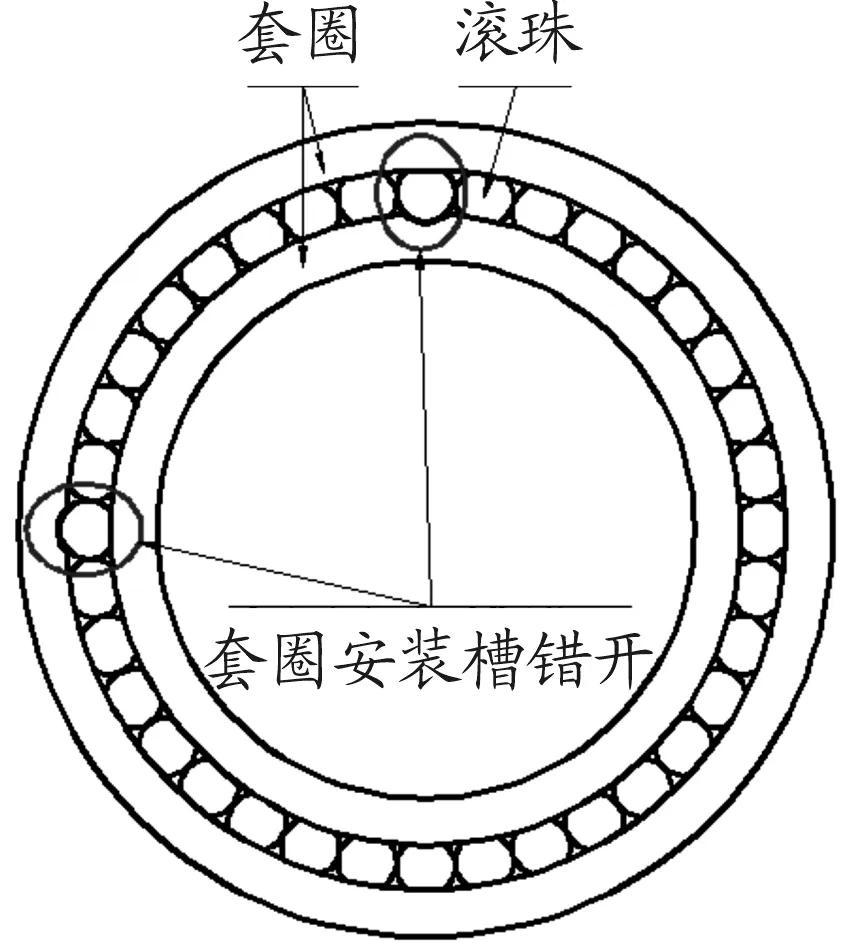
圖3 滾珠工作時安裝槽位置關系示意圖

滿裝球支撐時，滾珠數量計算原理圖如圖4所示。圖4中，ri為內滾道溝底半徑，r0為外滾道溝底半徑，r1為滾珠中心圓周半徑，r2為滾珠半徑，β為單個滾珠所占圓周角的一半。

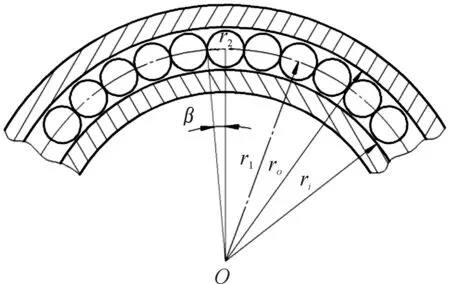
圖4 滾珠數量計算原理示意圖

根據圖4，可得滾珠數量的計算推導方程組為：

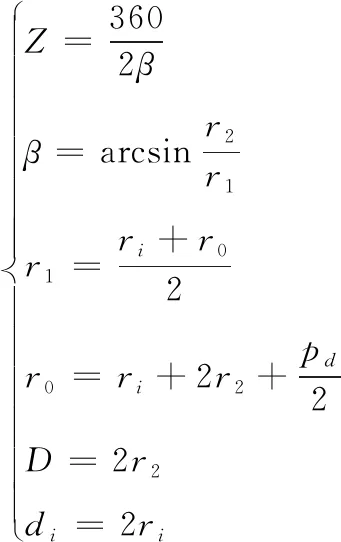
(1)

根據方程組(1)推導得出滾珠數量對應的關系式為：

(2)

式(2)中：Z為滾珠數量；di為內滾道溝底直徑；D為滾珠直徑；pd為滾珠與滾道之間的徑向游隙。

采用滿裝球支撐時，相同尺寸條件下的滾珠數量增多，在相同載荷作用下，單一滾珠與滾道的接觸載荷減小，接觸應力降低，從而隔轉平臺的抗過載能力增強。

1.2 隔轉平臺結構設計

采用滿裝球支撐方式，并根據隔轉平臺支撐的彈道修正引信功能件的結構和尺寸要求，對隔轉平臺進行了結構設計，其三維模型如圖5所示，描述各零件之間裝配關系的內部結構如圖6所示。

圖5 隔轉平臺整體模型示意圖

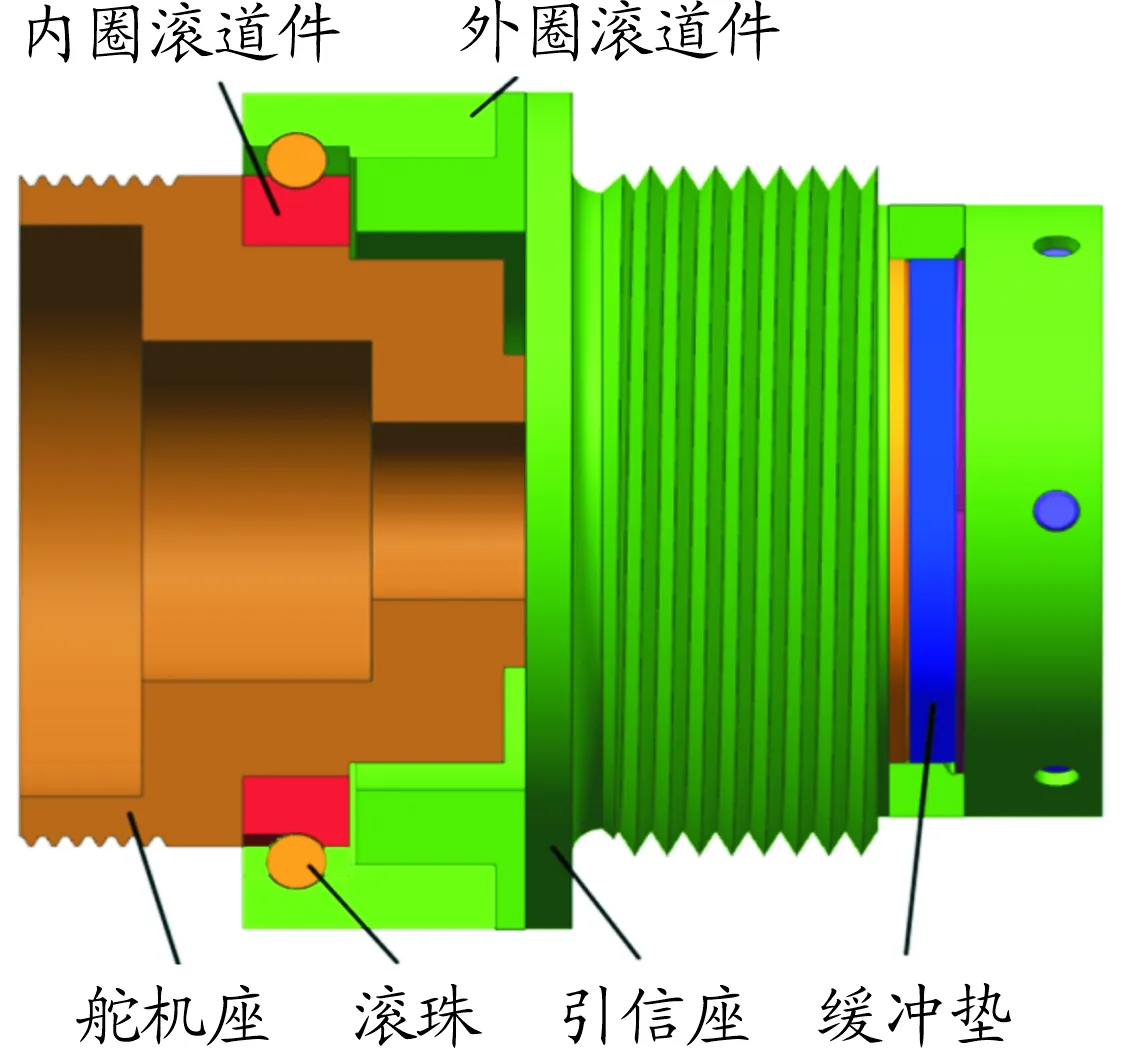
圖6 隔轉平臺內部結構示意圖

隔轉平臺的內外圈滾道之間裝填有最大數量的滾珠，通過滾珠直接支撐引信座與舵機座的相對轉動，實現彈道修正所需的旋轉隔離功能。緩沖墊可以通過變形吸能減小作用到滾珠上的載荷峰值。

2 動靜耦合有限元仿真方法

以影響隔轉平臺過載環境的因素為控制條件，綜合考慮軸向和徑向過載以及身管彎曲變形對彈體運動的影響，耦合彎曲身管的靜力學仿真與彈體的動力學仿真，將身管在重力作用下的彎曲變形作為彈體動力學仿真的控制條件，實現對彈體在彎曲身管內運動的模擬，進而實現對隔轉平臺過載環境的模擬，獲得隔轉平臺的動力學響應，以此作為隔轉平臺強度優化分析的依據[15-18]。

2.1 仿真模型建立

為了模擬彈體在彎曲身管內的運動過程，首先根據尺寸要求利用三維軟件UG建立彈體和身管的仿真模型。彈體仿真模型包括引信頭、隔轉平臺、常規引信組件、炸藥、彈殼和彈帶等，如圖7所示。身管仿真模型如圖8所示。

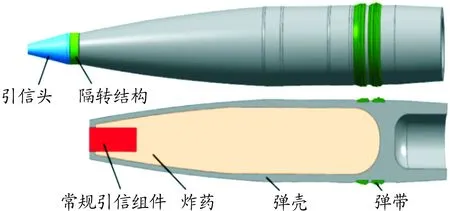
圖7 彈體仿真模型示意圖

2.2 仿真設置

仿真單元類型選擇三維實體單元中的六面體單元[19]，材料選擇雙線性隨動塑性材料模型[19]，關鍵部件材料參數如表1所示，網格劃分如圖9所示。在緊固連接無相對運動的部件之間設置固連接觸，在相互接觸有相對滑動的部件之間設置光滑接觸[19]。

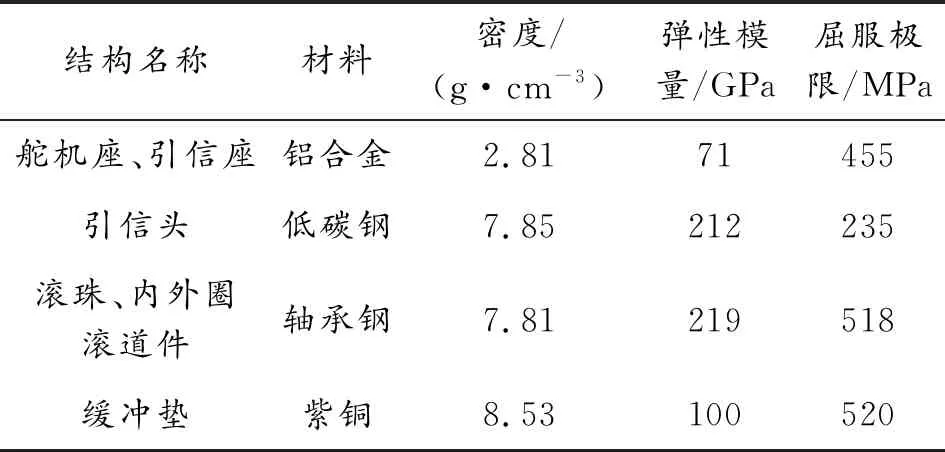
表1 材料參數

圖9 網格模型示意圖

身管靜力學仿真的載荷輸入為重力加速度，其施加在身管的所有節點上。彈體在身管內運動的載荷輸入包括彈體加速度和彈帶轉矩，由于本仿真針對的是彈載部件的過載問題，仿真所用的載荷曲線針對的是使彈載部件產生過載的主要膛壓段，忽略了彈帶擠進作用時間段以及膛壓相對較低對彈載部件過載影響很小的時間段，輸入的彈體加速度和彈帶轉矩載荷分別如圖10和圖11所示，曲線數據將作為仿真的輸入載荷分別加載到彈殼和彈帶的節點上。

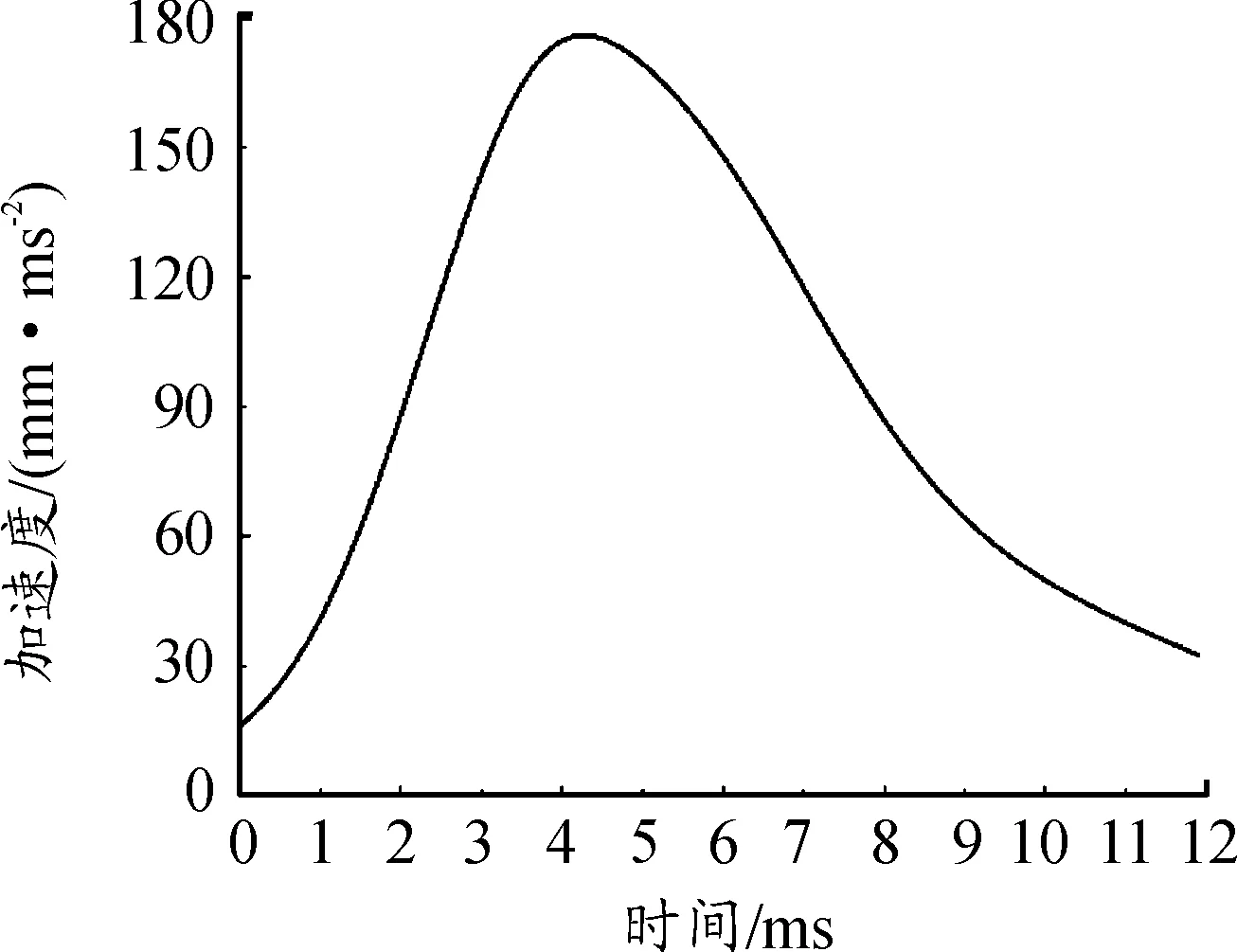
圖10 彈體加速度曲線

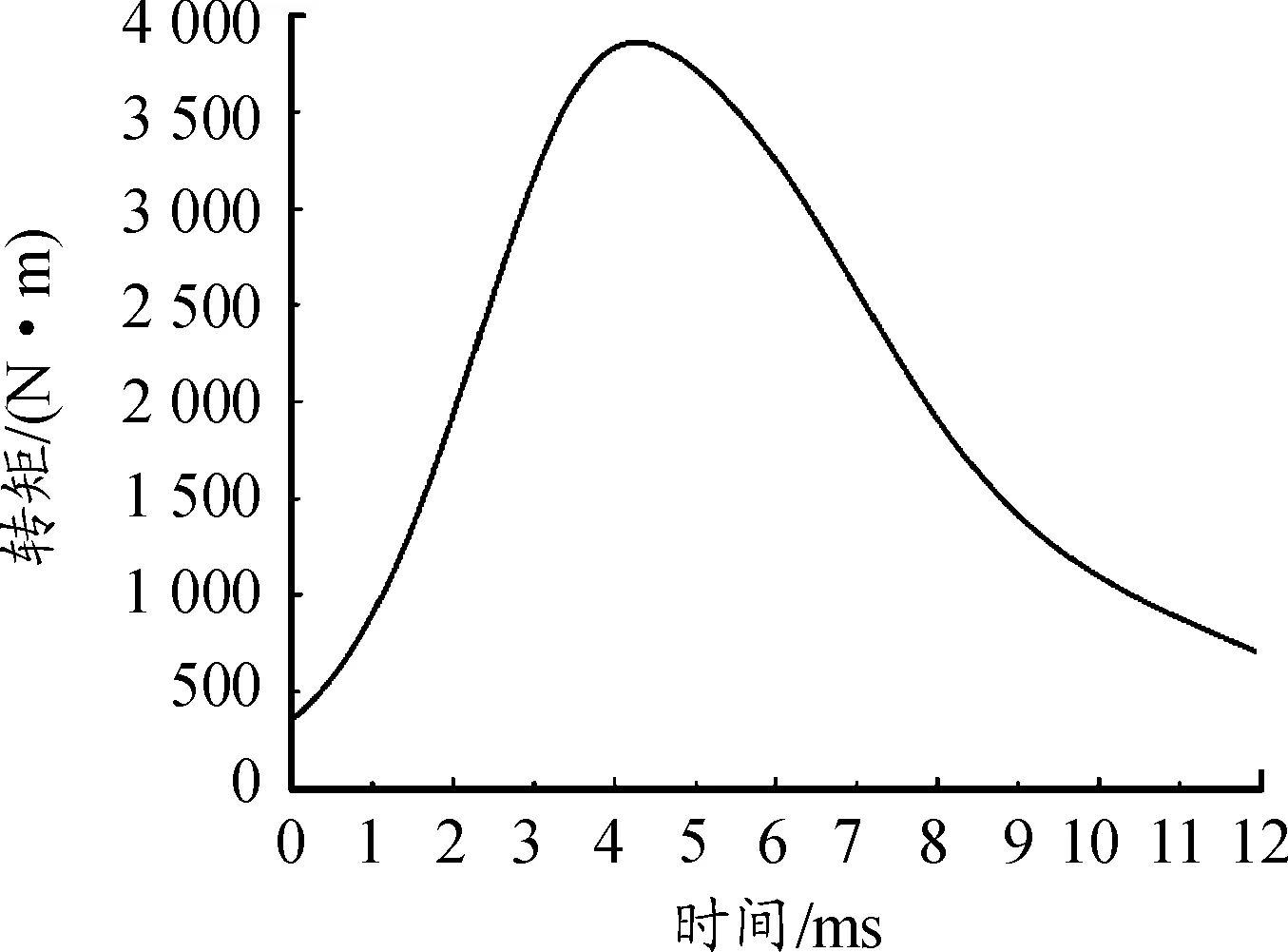
圖11 轉矩曲線

通過仿真獲得炮彈在身管內運動的速度曲線如圖12，出炮口時的軸線速度為1 016 m/s，接近于實際射擊時彈體的出炮口速度，因此，相同時間條件下，通過仿真模擬的彈體過載加速度與實彈射擊時彈體的過載加速度相比，偏差不大，通過此仿真方法模擬炮彈的發射過程可以用于隔轉平臺的結構強度校核。

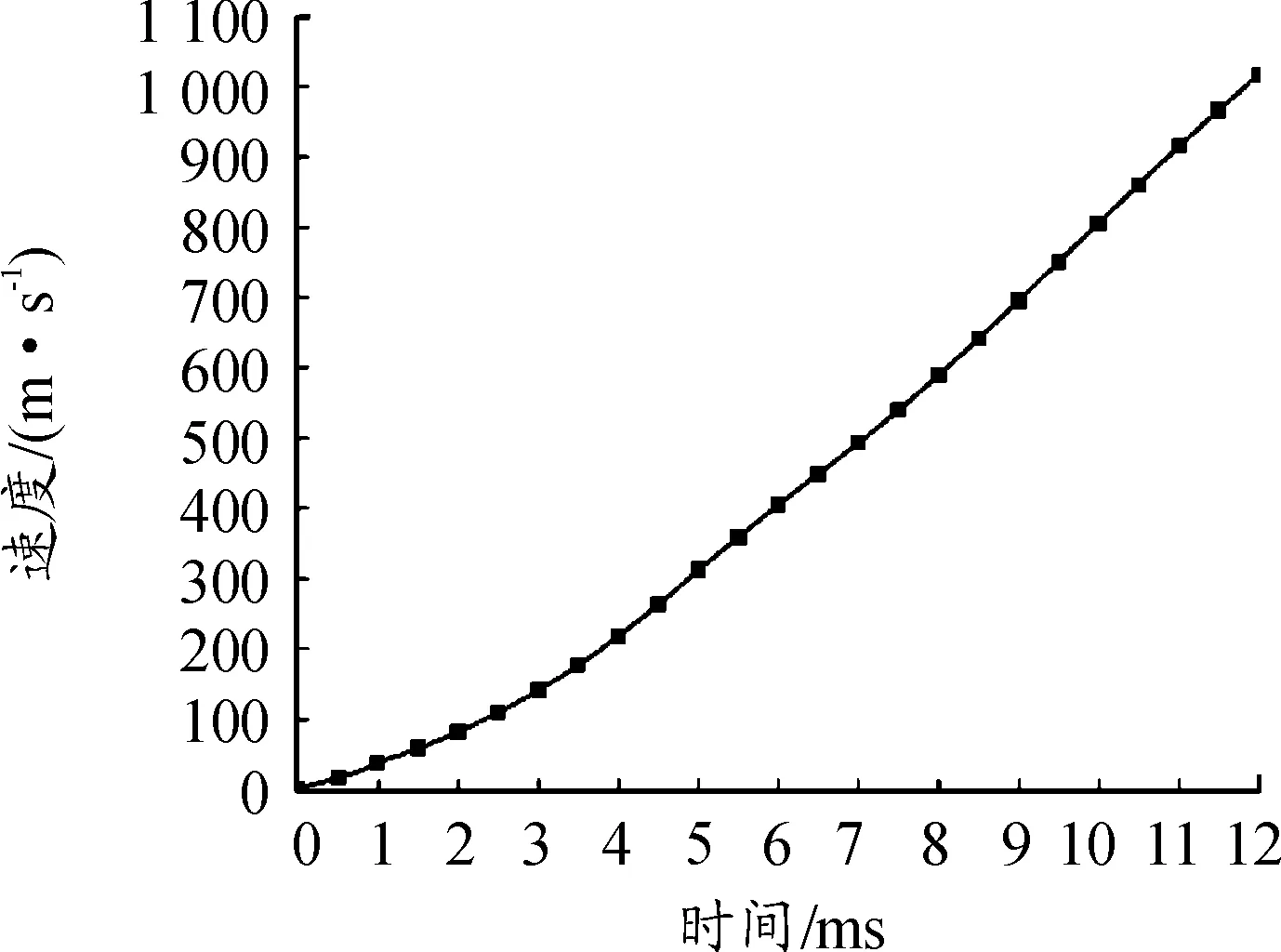
圖12 彈體速度曲線

3 隔轉平臺參數優化分析

基于已有研究可知，隔轉平臺中的滾珠以及內外圈滾道是隔轉平臺中的承載薄弱部件[20-21]。因此，對隔轉平臺的參數優化，提高其抗過載能力，主要是對隔轉平臺中的滾珠和內外圈滾道的參數進行優化。

3.1 隔轉平臺優化參數選取

根據Hertz接觸理論可知，在力的作用下滾珠與滾道接觸變形后的表面是一個旋轉橢球面，橢圓接觸區內，最大應力出現在幾何中心處[22]。在徑向和推力載荷聯合作用下的滾珠與滾道最大接觸應力計算公式為[22]：

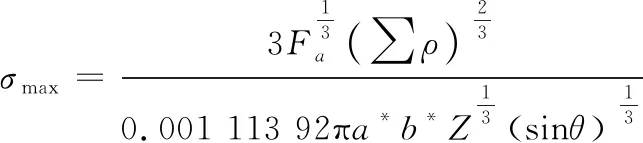
(3)

式(3)中:Fa為軸向推力載荷;Z為滾珠數量; ∑ρ為曲率和;a*、b*都是F(ρ)(曲率差)的函數，其量綱為1，實際應用時可以根據F(ρ)查對照表和對照圖獲得具體數值;θ為接觸角，需要通過迭代進行求解。滿足的迭代方程為：

(4)

式(4)中：D為滾珠直徑；K為軸向位移常數，通過總曲率B=fi+f0-1(f0和fi分別為內外圈滾道的溝曲率半徑系數)查表獲得；θ0為滾珠與滾道的初始接觸角，其計算公式為：

(5)

式(5)中，Pd為徑向游隙。

滾珠與內圈滾道接觸時的曲率和與曲率差分別為：

(6)

(7)

滾珠與外圈滾道接觸時的曲率和與曲率差分別為：

(8)

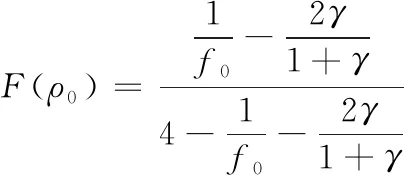
(9)

根據本節推導公式，分析滾珠與滾道接觸最大應力的影響因素傳遞關系如圖13所示。

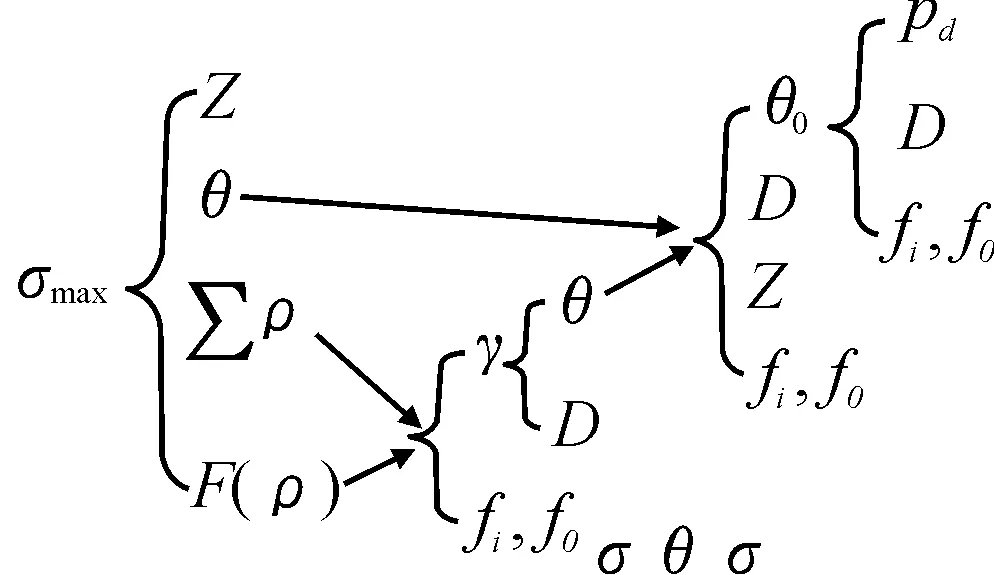
圖13 最大應力影響因素傳遞關系圖

圖13中，從左至右依次是最大應力影響因素的傳遞關系，可以發現，滾珠直徑D、滾珠數量Z、滾珠與滾道之間的徑向游隙pd以及內外圈滾道的溝曲率半徑系數fi和f0等結構參數是影響滾珠與滾道最大應力的基本因素，這些因素將直接決定著最大應力的大小。

為了使內外圈滾道的壽命相同，在設計時需要控制內外圈滾道的溝曲率半徑系數，使滾珠與內外圈滾道的最大應力相等[23]。

根據式(3)可知，滾珠與內圈滾道接觸時的最大應力為：

(10)

同理，滾珠與外圈滾道接觸時的最大應力為：

(11)

根據等應力要求σmaxi=σmax0，即滿足：

(12)

根據圖13各因素之間的影響傳遞關系可知，在滾珠數量Z、滾珠直徑D以及徑向游隙pd一定的前提下，式(12)中的變量僅剩下內外圈滾道的溝曲率半徑系數f0和fi，因此對每一個確定的fi通過式(12)都可以得到一個對應的f0。因此分析滾道溝曲率半徑系數對隔轉平臺中接觸最大應力的影響時，可以僅將fi或f0作為變化條件進行研究。

基于以上分析，研究隔轉平臺中滾珠與滾道的結構參數對最大應力的影響規律時，可以將Z、D、pd、fi作為變化參數進行分組研究，分析每個參數取不同參數值時對應的最大應力變化情況。

參數的選取依據同尺寸深溝球軸承參數并按照設計尺寸要求進行調整。優化時，同一參數對應的不同參數值在尺寸要求范圍內按照等差序列進行選取，如表2所示。

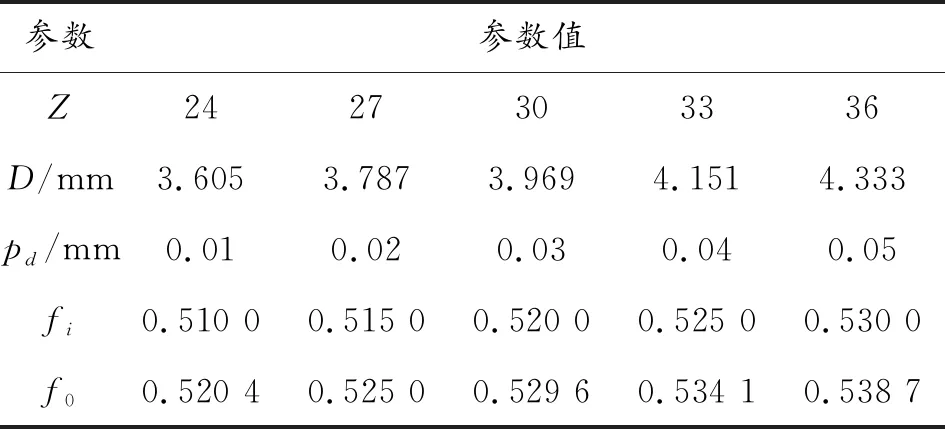
表2 優化時各參數對應的不同參數值

3.2 滾珠數量優化分析

根據表2，取D=4.333 mm，fi=0.515，f0=0.525，pd=0.04 mm，并保持不變，僅改變滾珠的數量設計了5組仿真方案，如表3所示。仿真后，獲得不同方案最大應力單元的應力分布曲線如圖14所示，最大應力值如圖15所示。

由圖14和圖15可知，隨著滾珠數量的增加，最大應力值呈遞減趨勢變化，并且在24≤Z≤30段內，衰減速度大，在30≤Z≤36段內，衰減速度變小，到Z=36時，最大應力值降為722 MPa。

表3 不同仿真方案的滾珠數量

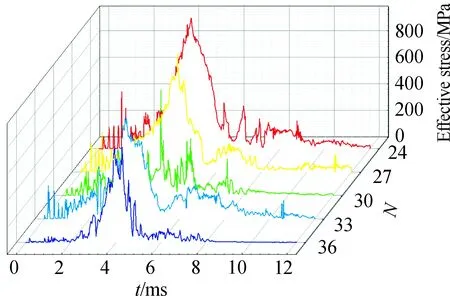
圖14 不同滾珠數量時的應力分布曲線

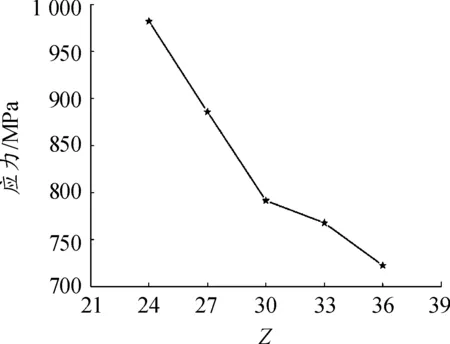
圖15 不同滾珠數量時的最大應力值曲線

3.3 滾珠直徑優化分析

根據表2，取Z=36，fi=0.515，f0=0.525，pd=0.04 mm，并保持不變，僅改變滾珠直徑，設計仿真方案如表4所示。仿真后，獲得不同方案最大應力單元的應力分布曲線如圖16所示，最大應力值如圖17所示。

表4 不同仿真方案的滾珠直徑

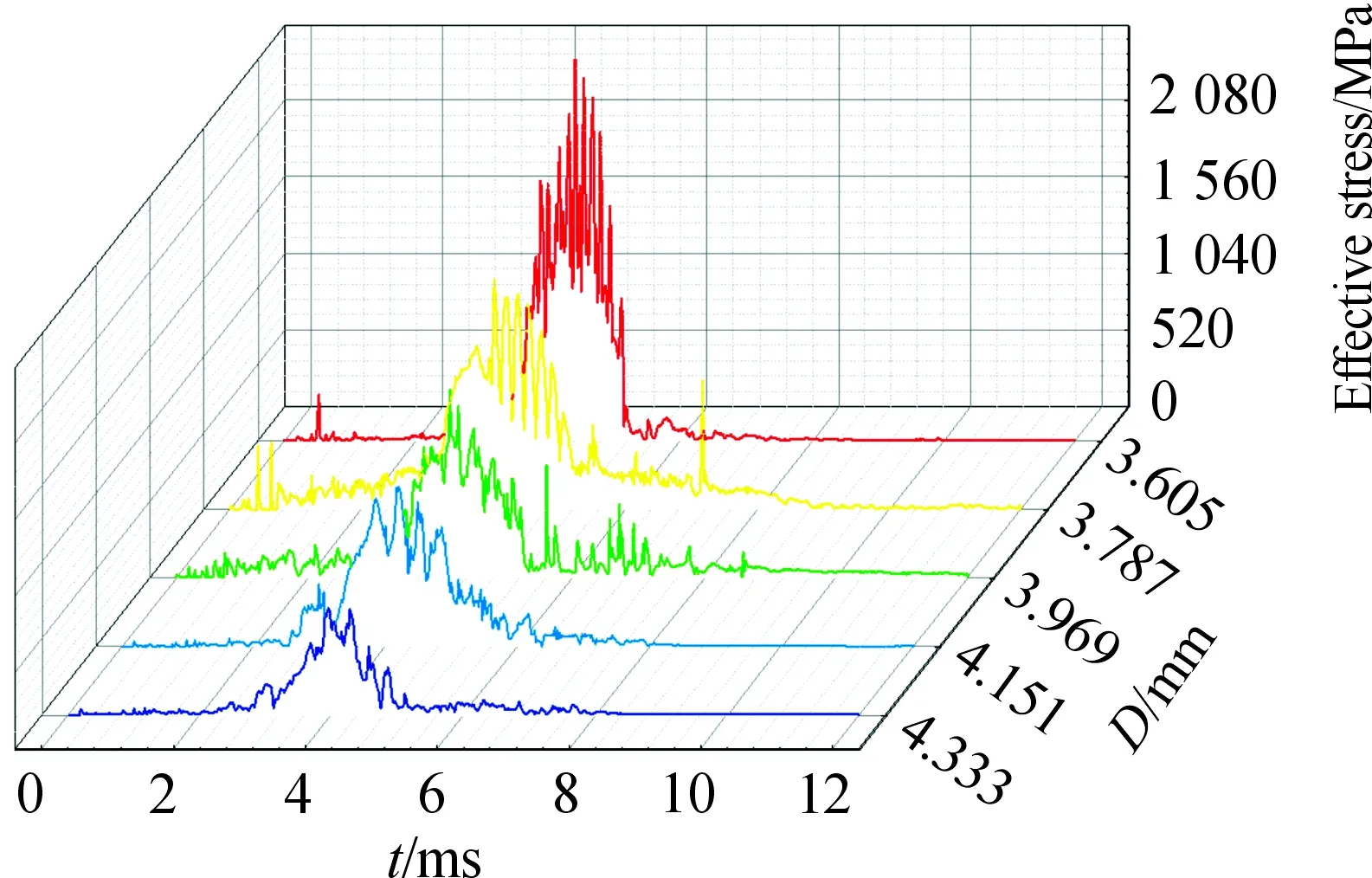
圖16 不同滾珠直徑時的應力分布曲線

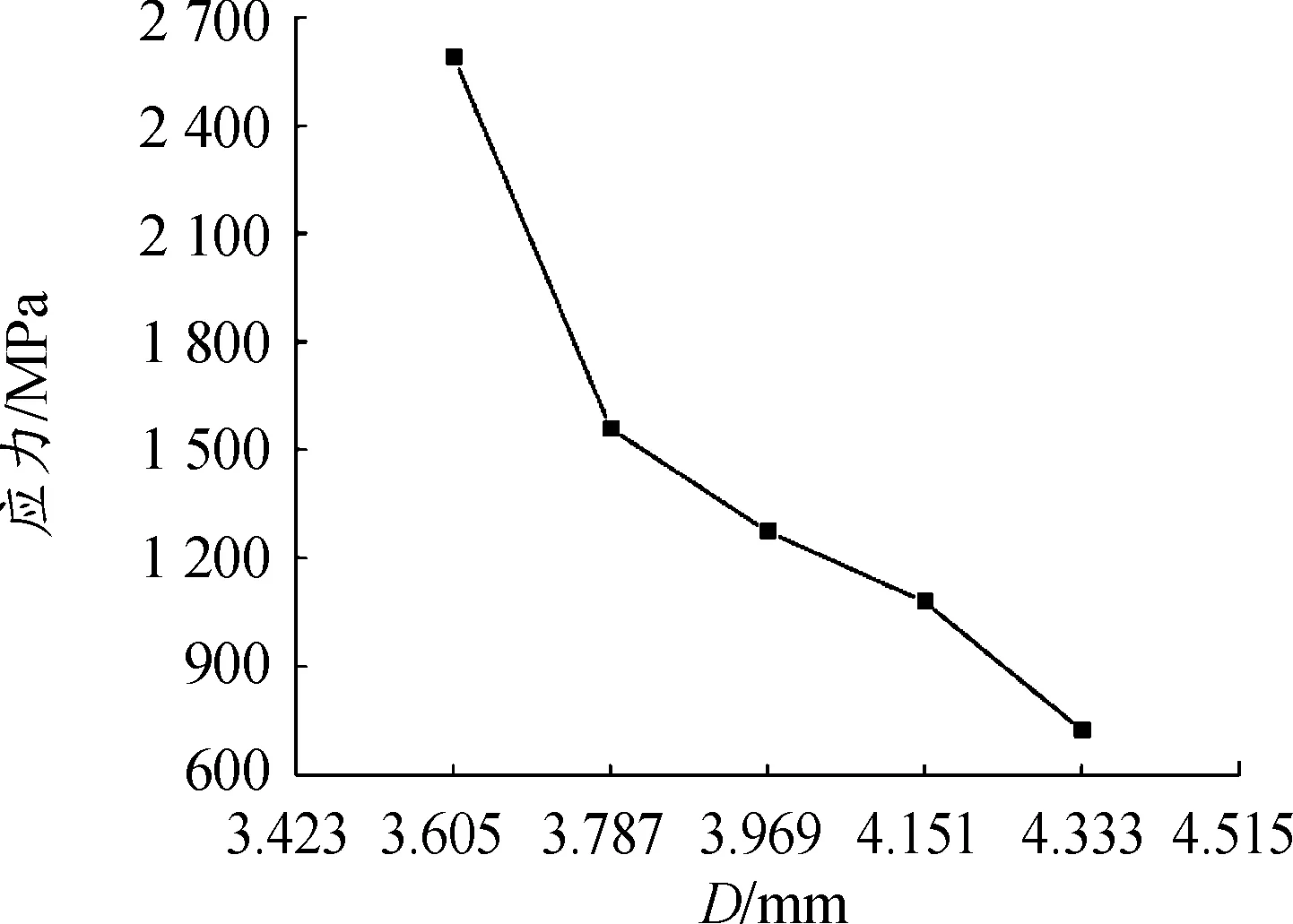
圖17 不同滾珠直徑時的最大應力值變化曲線

根據圖16和圖17可知，隨著滾珠直徑的增大，最大應力值呈遞減趨勢變化，并且在3.605≤D≤3.787范圍內，減小速度大，在3.787≤D≤4.333范圍內，減小速度小，到D=4.333時，最大應力值減小到720 MPa。

3.4 徑向游隙優化分析

根據表2，取Z=36，D=4.333 mm，fi=0.515，f0=0.525，并保持不變，僅改變徑向游隙，設計仿真方案如表5所示。仿真后，獲得不同方案最大應力單元的應力分布曲線如圖18所示，最大應力值如圖19所示。

表5 不同仿真方案的徑向游隙

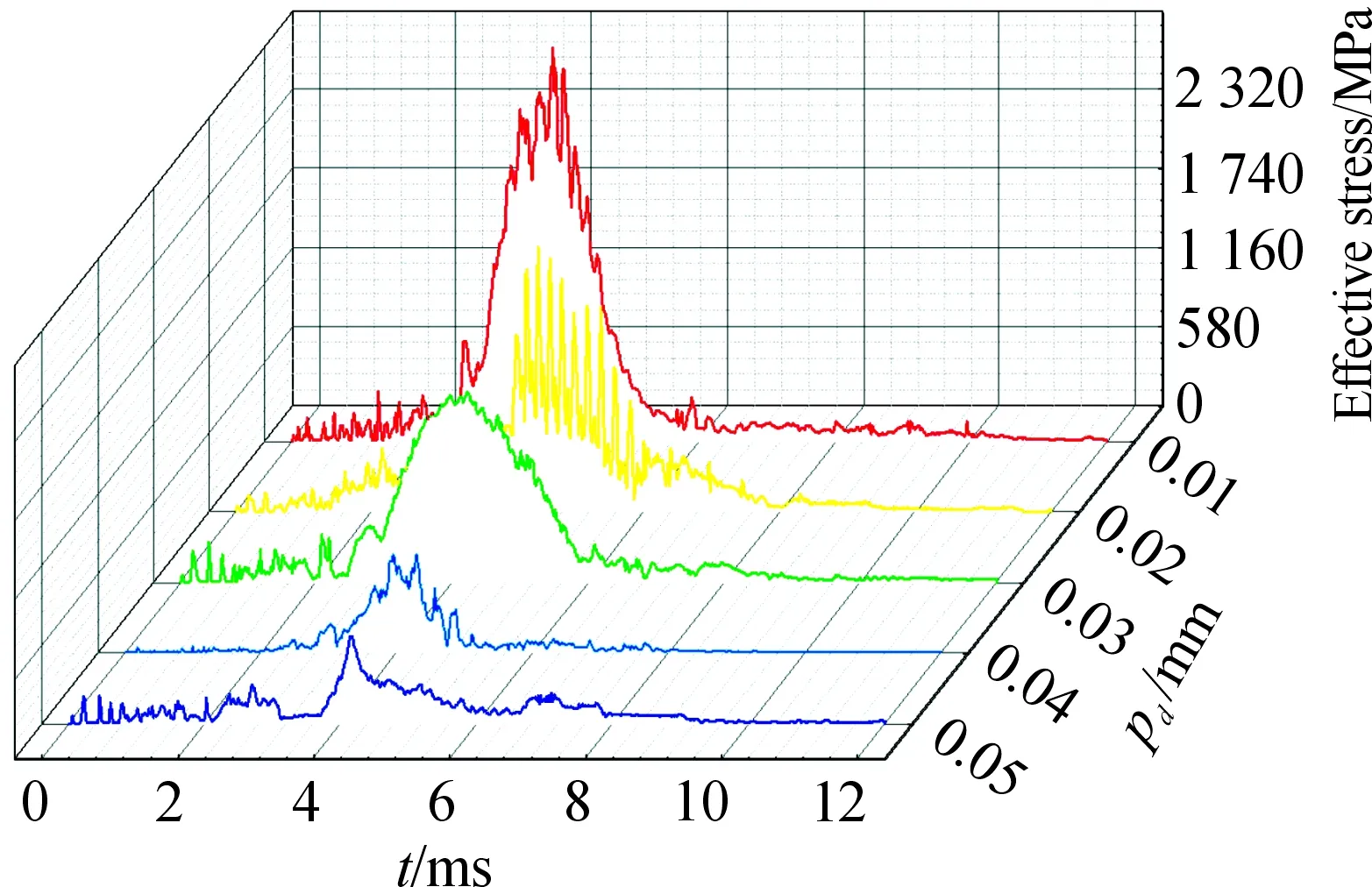
圖18 不同徑向游隙時的應力分布曲線

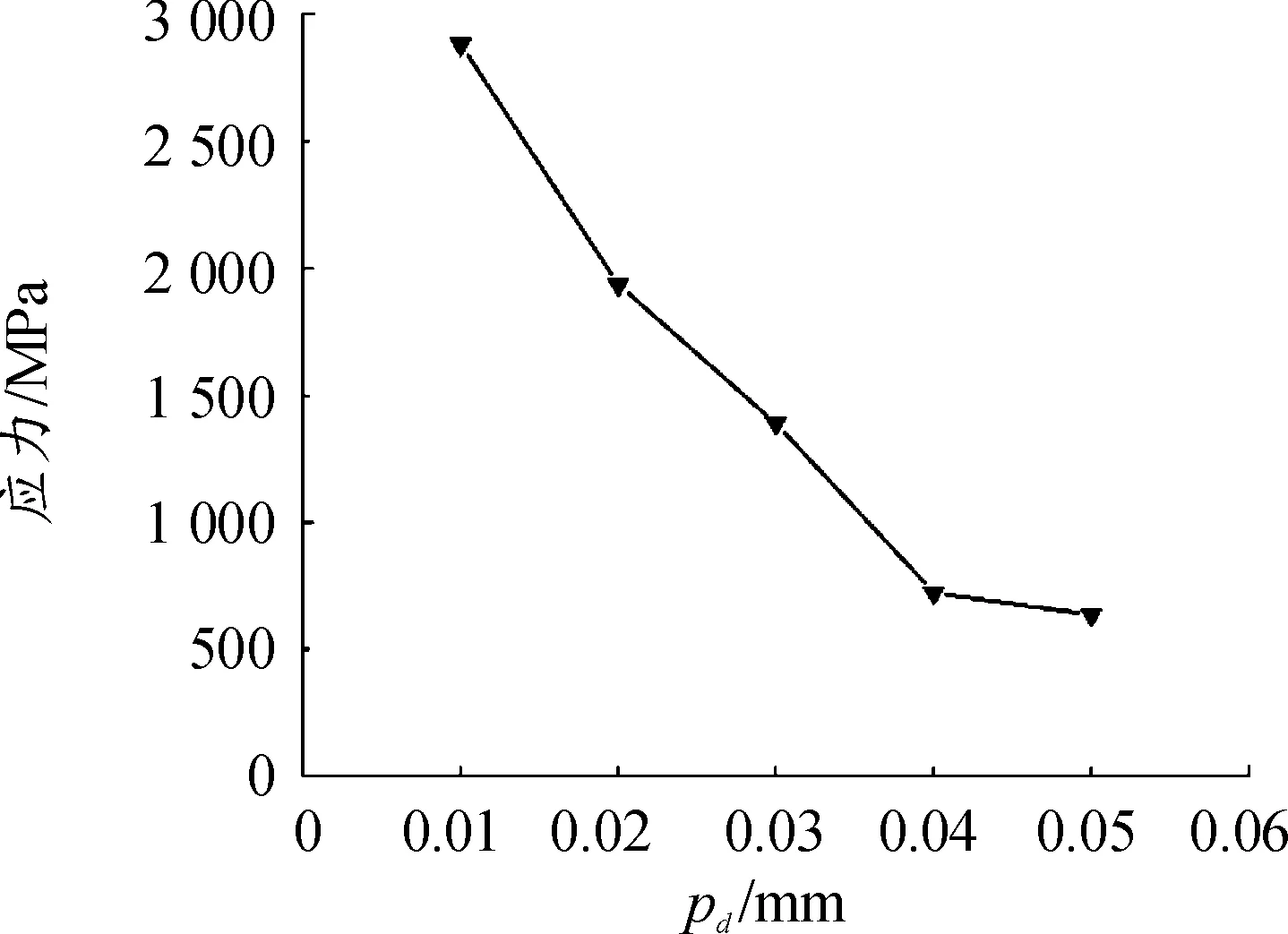
圖19 不同徑向游隙時的最大應力值曲線

根據圖18和圖19可知，隨著徑向游隙的增大，最大應力值呈減小趨勢變化，在0.01≤pd≤0.04范圍內，減小速度快，在0.04≤pd≤0.05范圍內，減小速度變慢，當pd=0.05時，最大應力值減小到635 MPa。

3.5 滾道溝曲率半徑系數優化分析

由圖19可知，徑向游隙取0.04和0.05兩種方案時，最大應力值相差很小，同時考慮到徑向游隙過大會導致引信頭的旋轉波動變大，因此，優化滾道溝曲率半徑系數時，取Z=36，D=4.333 mm，pd=0.04 mm，并保持不變，僅改變內外圈滾道的溝曲率半徑系數，設計5組仿真方案如表6所示。仿真后，獲得不同方案最大應力單元的應力分布曲線如圖20所示，最大應力值如圖21所示。

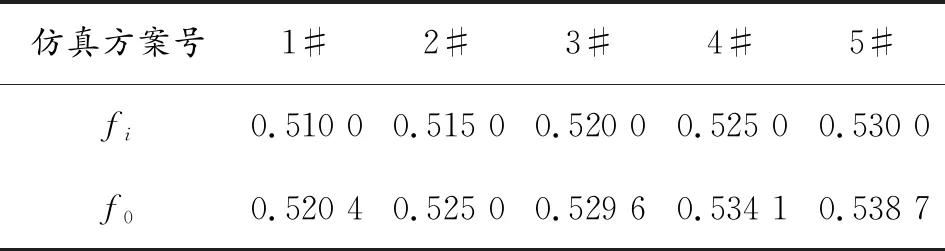
表6 不同仿真方案的內外圈滾道溝曲率半徑系數

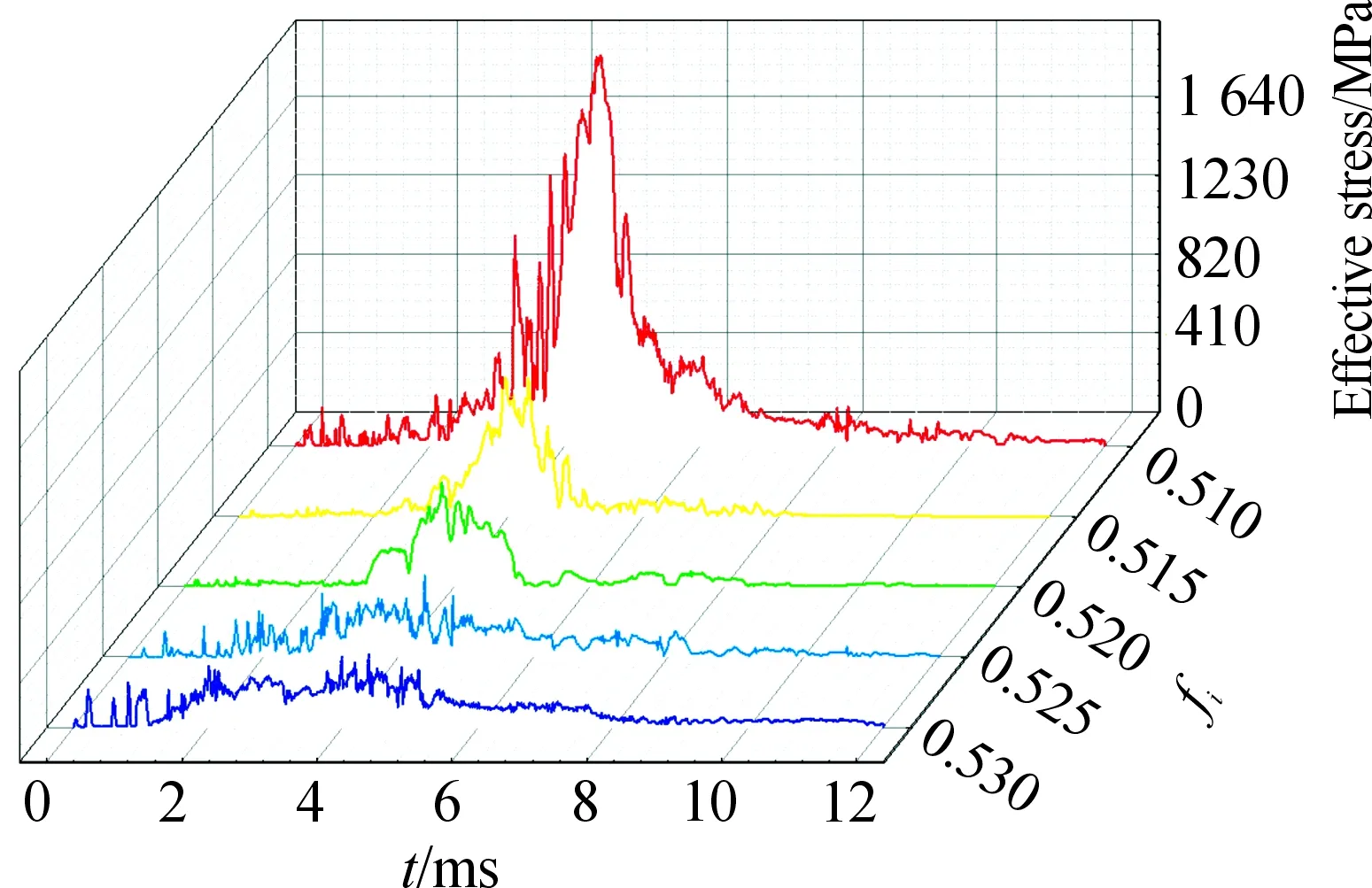
圖20 不同溝曲率半徑系數時的應力分布曲線

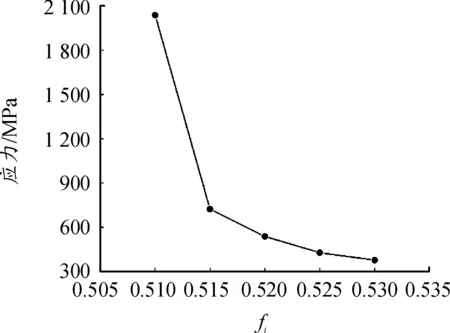
圖21 不同溝曲率半徑系數時的最大應力值曲線

根據圖20和圖21可知，隨著溝曲率半徑系數的增大，最大應力值呈遞減趨勢變化，并且在0.510 0≤fi≤0.515 0范圍內減小速度大，在0.515 0≤fi≤0.530 0范圍內減小速度小，當fi=0.530 0時，最大應力值減小到377 MPa。同時可以發現，當fi=0.525 0時，最大應力值為427 MPa，其與fi=0.530 0時的最大應力值377 MPa均小于材料的屈服極限518 MPa，能夠滿足屈服強度要求。

4 結論

1) 在設計參數范圍內，隨著滾珠數量Z、滾珠直徑D、徑向游隙pd、內圈滾道溝曲率半徑系數fi的增加，均可以使滾珠與滾道的最大應力減小。

2) 當fi=0.5150、f0=0.5250時，通過優化滾珠數量Z、滾珠直徑D和徑向游隙pd等結構參數，并不能使最大應力下降到材料屈服極限以下。

3) 當Z=36、D=4.333 mm、pd=0.04 mm時，通過優化滾道溝曲率半徑系數，可以使最大應力下降到材料屈服極限以下。

4) 獲得了兩種滿足屈服強度要求的隔轉平臺方案。分別為：參數滿足Z=36、D=4.333 mm、pd=0.04 mm、fi=0.525 0、f0=0.534 1時的隔轉平臺方案和參數滿足Z=36、D=4.333 mm、pd=0.04 mm、fi=0.530 0、f0=0.538 7時的隔轉平臺方案。