非定常空化流動及其誘導振動特性研究綜述

吳 欽,郭一夢,劉韻晴,王國玉

(北京理工大學 機械與車輛學院,北京 100081)

0 引 言

當液相介質中局部壓力降至其飽和蒸氣壓以下時,液相中將產生大量充滿氣體和蒸汽的空穴,這些空穴是一些單個的球形空泡,或是多個空泡形成的空泡群以及外形不規則的空腔。這是一個復雜、不穩定、多尺度和多相的流動現象,即空化[1-2]。從力學的角度上看,空化是液體在足夠大的應力作用下發生的一種斷裂現象,因此空化亦可被認為是液體的一種力學破壞形式[3]。空化流動是高速水動力學的核心關鍵問題,具有明顯的非定常特性,同時包含了多種復雜流動現象,如多相流、湍流和可壓縮流動等[4],這也使得空化成為各種工程應用上一個極大的挑戰。

空化涉及國民經濟發展和國家安全等工程領域關鍵技術的突破,空化的發生會引起壓力脈動、負載突變,改變系統性能、破壞過流部件表面和產生振動噪聲,嚴重影響機械系統的高效安全運行。在水力機械領域,空化引起的振動是影響水電機組和大型排灌泵站安全運行的主要問題[5-6],梢渦空化是限制螺旋槳等水下推進裝置高效航行的根本原因[7]。在水中兵器領域,為提高魚雷和新型潛艇的綜合性能,亟需解決空泡噪聲這一關鍵問題[8]。在水下發射領域,潛射導彈在出水過程中,受到復雜水環境的影響,其運動速度和周圍流場參數不斷變化,彈體表面形成具有強非定常特性的空穴,伴隨著空穴的發展、斷裂和脫落,彈體所受載荷十分復雜[9]。在航空航天領域,需采用具有高功率密度的高轉速渦輪泵輸送液體燃料,提升渦輪泵及其前裝誘導輪的空化性能對保障大功率火箭發動機安全具有重大意義[10]。另一方面,超空泡減阻技術在水中兵器領域的應用極大地改變了海洋作戰局面,如超空泡魚雷減阻技術,使魚雷在高速運行過程中產生超空泡并包裹彈體,從而降低魚雷摩擦阻力[11-12]。

綜上所述,考慮水力機械內部的振動和噪聲等問題、航行體和水下兵器的創新研制和隱蔽性問題以及其他領域的關鍵技術問題,對空化現象的研究具有重要的理論和工程應用價值。本文首先綜述了空化流動現象的實驗和數值研究現狀,然后進一步對空化誘導結構振動特性及其與結構動態響應的耦合作用研究進行了綜述,并對非定常空化流動及其誘導振動特性研究的發展趨勢進行了展望。

1 空化流動的研究現狀

1.1 空化流動的試驗研究

實驗研究一直是人們探索復雜空化現象與空化流動機理的基本方法。1896年Parsons建立第一個空化水洞,開始進行螺旋槳空化現象的觀察研究[13]。Knapp[14]基于大量的空化實驗觀測,根據空化發生部位和動力特性將空化分為游移空化、固定空化、旋渦空化和振蕩空化。Brennen[1]等按空化的發展階段特征將其劃分為初生空化、片狀空化、云狀空化和超空化。圖1給出了不同水翼迎角和流場空化數條件下,繞NACA66水翼的典型空化形態及平均空泡長度。初生空化階段,水翼前緣吸力面開始出現游離狀空泡,其發生和發展過程具有一定隨機性。隨著空化數的減小,水翼吸力面空泡區域增大,形成了相對穩定的附著型空穴,同時空穴尾部存在小尺度空泡的快速形成與脫落。當空化數進一步降低時,空化發展至云狀空化階段,附著型空穴斷裂,大尺度云狀空泡團形成并發生周期性脫落和潰滅現象。繼續降低空化數時,繞水翼空化流動由云狀空化發展至超空化階段,空泡覆蓋了整個翼型并保持較穩定的狀態。在此基礎上,Tulin[15]總結了超空化水翼的翼型,建立了超空化的理論基礎,提出了一種Hydronautics低阻力超空化水翼。與一般水翼相比,Hydronautics超空化水翼是一種易于超空化產生的特殊的水翼,兩種水翼的前后緣形狀正好相反,Hydronautics超空化水翼的迎流面為一尖角,尾部為一鈍剖面。Li等[16]采用高速全流場顯示技術觀測了繞Hydronautics超空化水翼的空化流動,如圖2 所示。Zhang等[17]進一步采用歐拉和拉格朗日方法對空化流場旋渦結構進行了分析。對于一般繞水翼的片狀空化,其頭部即片狀空穴前緣一般附著在翼型吸力面壁面上,而且位置基本不隨時間的變化而變化。而由于具有尖銳前緣的超空化水翼為不良繞流體,實驗中基本沒有觀察到此階段空化的前緣附著現象,而是在尾流中出現兩旋轉方向相反的旋渦,上渦沿順時針旋轉,下渦為逆時針旋轉。隨著空化數的降低,空化渦街現象趨于明顯。當空化數降至σ＝0.87 時,出現明顯的云狀空化。同一般水翼的附著型空化一樣,空化開始充滿整個吸力面,并形成周期性的空化云脫落。不同的是,其后部仍有上下渦配對之后形成的脫落。隨著空化數的進一步降低形成超空化時,空泡的發展經歷空穴形成、兩相共存和完全發展階段。

圖1 典型工況下繞NACA66水翼典型空化形態及其平均空泡長度[18]Fig.1 Cavity patterns and average cavity length for typical cavitation around NACA66 hydrofoil[18]

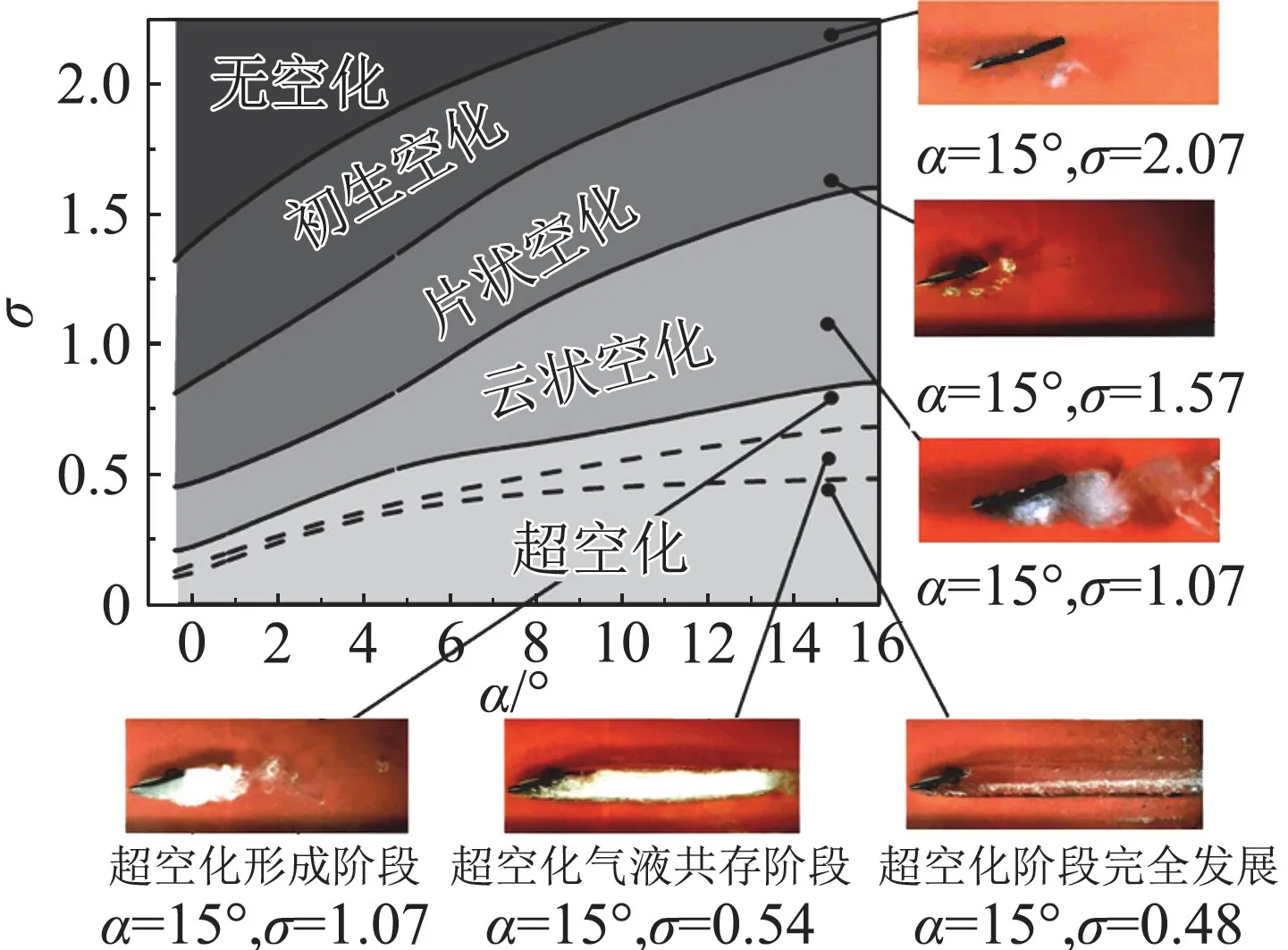
圖2 典型工況下繞Hydronautics超空化水翼典型空化形態及其平均空泡長度[18]Fig.2 Cavity patterns and average cavity length for typical cavitation around Tulin hydrofoil[18]

隨著水洞、水池實驗研究的大量開展以及各種先進測試設備與技術的出現,人們對空化現象的認識不斷深入。Arakeri和Acosta[19]、Katz[20]分別基于紋影法和全息顯示技術研究了繞回轉體流動分離與初生空化流動,發現了空化初生與邊界層流動的相互關系,結果表明空化發生在流動分離區域,且湍流再附著區域對空化初生有著較大影響。Guennoun等[21]采用微型壓力傳感器和高速攝像機同步測量技術研究了繞水翼泡狀空化流場特性,揭示了游離型空泡的形成機理和周期性水動力特性。Kubota[22]采用高速攝像機和激光多普勒測速儀(Laser Doppler Velocimetry,LDV)觀測了繞水翼云狀空化流場結構的演變情況,基于條件采樣技術發現了最大渦量分布與空化核的關系,初步探究了云狀空化流動中空化與旋渦結構的相互作用關系。Liu等[23]利用氙氣閃光燈和高速攝像機對繞二維Clark-Y 型水翼空化流動進行了觀測,并利用激光多普勒測速技術對流場空泡內外區域的液相速度進行了測量。結果表明,空泡內部的平均速度分布與邊界層內單向流動的平均速度分布基本一致,但水翼近壁區域的反向射流具有強烈的波動性和間歇性。Stutz和Rebound[24-25]發展了一種雙探針光學探頭以測量流場空泡內部含氣量、流速和空泡尺寸等空化流動參數,并應用此技術對文丘里管內不同空化數和雷諾數條件下的空化流動進行了研究,進一步闡明了空泡發展、近壁面反向射流和大尺度空泡團脫落的流動機理。Arndt[26]等應用數字式粒子圖像測速(DPIV)技術,對繞NACA0015水翼單相流動的尾跡流域進行了測量,研究表明空化的發生顯著改變流場結構,水翼尾緣低速尾跡區域明顯擴大。張博[27]等采用動態應變儀與箔式中溫電阻應變片組成測量電橋測量了空化流場中不同空化階段水翼所受的升阻力,揭示了亞空化流動下的不同空化階段的非定常水動力特性及其與空穴形態間的關系。Matthieu 等[28]利用三維粒子測速技術(Stereo Particle Image Velocimetry,SPIV)對不同流速、迎角和間隙寬度工況下水翼下游三個平面內的來流速度場進行了測量,研究了不同來流工況的間隙泄漏渦結構特征,闡明了特定間隙寬度條件下的最大渦流強度及間隙渦空化流動機理。Che[29]用高速攝像機和壓力測量裝置同步觀測了水翼在過渡空穴振蕩時期空穴脫落和回射流現象。

綜上所述,由于非定常空化流動中水-汽自由表面的干擾和反光等問題,傳統的實驗觀測仍局限于對空泡外圍及尾流的觀測。Wang等[30]基于高速全流場顯示和瞬時粒子圖像測量TR-PIV 系統,發展了通氣空泡內部流動結構的精細化測量技術,實現了對通氣空泡流型、復雜湍流旋渦結構、運動特性的準確觀測與測量。近年來,高時間分辨率的X 光密度測量以及X 光誘導的粒子相關測速技術已揭開了空泡內部流場結構測量的序幕,并已成為空化流動實驗研究的主要發展方向。Ganesh[31]針對高雷諾數空化流場的瞬態密度測量,發展了一種采樣頻率在1k Hz以上的X 射線速度測量裝置,獲得了楔形體片狀空泡內水蒸氣體積分數的時空變化。

基于試驗技術的綜合應用,人們開始逐漸關注空穴的斷裂及空泡的脫落行為及其對空化水動力特性的影響。Kubota等[22]闡明了空化的微觀結構,確定了在空化的形成和發展過程中包含許多微小的氣泡集中渦,并提出了近壁反向射流的存在是空穴尾部不穩定的原因。Leroux等[32-33]基于實驗觀測和壓力測量等手段研究了非定常空化水動力穩定特性對空化發展及空泡斷裂脫落現象的影響,揭示了不同來流迎角條件下兩種不同的非定常空化流動水動力特性。Kjeldsen等[34]對空泡云團脫落和潰滅過程中的參數進行傅立葉變換分析,得到其頻譜相關特性。張博等[35]通過測量水翼表面壓力分布揭示了空穴在生長、斷裂、脫落過程的非定常水動力特性,綜合分析了水翼動力特性與空穴形態的內在關系。Kawanami等[36]應用高速攝像技術和壓力傳感器測壓技術研究了云狀空泡的非定常脫落機制,認為在云狀空化的非定常發展過程中,反向射流引發空泡的斷裂與脫落,并發現在附著空穴尾部區域放置障礙物可以抑制反向射流和大尺度云狀空泡團的形成,從而大幅減小水翼結構的繞流阻力和流動噪聲。圖3給出了云狀空化反向射流及大尺度空泡團脫落現象。如圖3(a)所示,局部片狀空化從水翼的前緣發展到x/c＝0.5的位置。在空泡發展過程中,空泡在尾緣處形成回射流,并從空泡尾緣兩側向空泡前緣中心移動。De Lange[37]和Franc[38]研究指出,根據空泡邊界動量守恒,回射流有垂直和沿空泡閉合線兩個分量。如圖3(b)所示,隨著云狀空泡的脫落,這兩束向上的流動相互碰撞,切斷了空泡的下游部分,并在剩余的空泡后緣形成一個楔形孔。云狀空泡繼續向下游移動,最終潰滅,如圖3(c)所示。Yang等[39]研究表明,反向射流和水翼吸力面的展向速度是導致云狀空化三維效應的主要因素。Foeth[40]指出,由于回射流對空泡脫落的重要影響,需要精確模擬回射流的方向和動量。

圖3 云狀空化反向射流[41]Fig.3 Re-entrant jet in cloud cavitation[41]

1.2 空化流動的數值模擬研究

隨著計算技術的發展,數值模擬成為空化研究的另一重要手段。最早的空化數值計算基于自由流線理論并應用速度圖法進行求解,假設空泡表面為自由流線,將空泡內部壓力視為常數,在求解過程采用空穴的閉合模型[42-43]。但該方法由于忽略空穴內部的流動,無法準確獲得非定常空化流動數值計算結果。隨后,大量學者針對空化流動的數值模擬開展研究,主要可分為兩大類,一類是界面追蹤法,另一類是基于Navier-Stokes(N-S)方程的數值計算求解法。

界面追蹤法假設空穴內部壓力恒等于汽化壓力,在汽液兩相界面應用運動學和動力學方程的邊界條件,迭代計算獲得界面位置。其中,邊界元計算方法應用較為廣泛[44-45],通常應用于定常附著型空化和超空化的流動計算,可以較好地預測空化流動的整體行為,但對空化形態的非定常變化和三維界面的追蹤模擬準確度不高。

基于N-S方程的數值計算求解法,需要結合多相流模型、湍流模型和空化模型。在多相流模型的研究中,目前廣泛應用的均相流模型認為整個空化流場由可變密度的單一流質組成,應用均質平衡流模型(HEM)建立一組偏微分方程來控制流體運動和狀態。Delannoy[46]最早提出基于壓力-混合密度耦合法對可變密度場進行定義,該方法對空穴附近的流場有一定效果,但由于忽略了氣液相間輸運方程,僅適于計算較穩定的附著型空化流場,無法捕捉空化流場中的復雜非定常湍流結構[47-48]。基于此,另一種處理方法是采用基于質量傳輸方程的模型來求解密度場,通過額外的傳輸模型求解流場中的汽相或液相的百分比,可以較好地模擬慣性力對空穴的生長、附著和發展的影響。考慮到空化流動的動力學特性、頻繁的相間交換等,Rayleigh[49]早在1917年比較系統地提出了空化理論,建立了在無限理想不可壓縮流體中球形空泡軸對稱潰滅的控制方程。Plesset[50]進一步研究提出了Rayleigh-Plesset方程,形成了空泡動力學理論基礎。再此基礎上,Kubota等[51]通過建立質量傳輸與壓強之間的關系提出了基于空泡動力學的質量傳輸方程,較好地描述了空泡生長和發展過程中的體積變化。國內外研究學者基于不同的假設,通過物理現象觀察或經驗方程式確定相應的蒸發與凝結系數控制相變化和傳輸強度,從而發展出不同的空化模型。大量學者基于Rayleigh-Plesset方程建立了表征質量傳輸與壓強變化關系的空化輸運方程,即相間傳輸率正比于飽和蒸汽壓與當地壓力之差的平方根。其中,Zwart[52]模型根據經驗將空泡半徑、空化核子等參數取為常數;Schnerr和Sauer[53]在模型中通過引入汽核體積分數考慮了單位體積內空化核子隨含氣率的變化;Singhal[54]綜合考慮了流場流動特性(表面張力、湍流脈動等)對汽液相間質量傳輸過程的影響,提出了全空化模型;Gerber[55]、Frobenius[56]、牟斌等[57]也在此基礎上結合經驗公式提出了相應的空化模型。此外,Merkle[58]、Kunz[59]等基于量綱分析和實驗現象觀測結果推導建立了空化輸運方程,結果表明相間質量傳輸率正比于飽和蒸汽壓與當地壓力之差的絕對值,并通過添加源項調節汽液相間傳輸,實現了水下航行體自然空化與通氣超空化流動的數值求解。在此基礎上,Senocak 和Shyy[60-61]提出了基于空泡界面動力學的質量傳輸模型(Interfacial Dynamic Model,IDM),從理論上消除了Merkle和Kunz模型中經驗系數對空化模型的影響,具有較高的精度。黃彪等[62]基于上述模型發展了一種基于混合密度分域的空化模型(Density modify based cavitation model,DMBM),在含汽量較大的區域內采用空泡界面動力學質量傳輸空化模型,以模擬空穴內部、汽液交界面的演變過程,而在含汽量較小的區域采用Kubota空化模型,以捕捉空泡團的旋渦脫落現象。圖4和圖5給出了不同模型預測的非定常空穴長度隨時間的演化情況,可以看出Kubota模型過早預測了空穴的斷裂,這是由于Kubota空化模型根據空泡動力學方程計算單個氣泡體積的擴散速度,假設空泡是均勻的徑向發展且不會相互作用。附著型空穴的發展和回縮、斷裂過程可以視為無數空泡體積變化的整體行為,對空穴內部的流場結構的特征差異不能很好的體現。采用IDM 空化模型所預測的附著空穴長度則一直比較穩定,相較而言,DMBM 模型對空穴發展的兩個典型階段均有比較客觀的描述,該模型結合了IDM 與Kubota空化模型在模擬云狀空化流動現象的優點,準確地模擬出附著在翼型前端穩定的含氣量相對較大的空穴與翼型尾部含氣量相對較低的不穩定的汽液兩相區,兩者動態界面非常明顯;此外,DMBM 空化模型合理地預測了空泡脫落時刻翼型尾部的不穩定脈動區,當反向射流發展到水翼前緣位置時,會切斷附著型空穴,導致空穴長度的驟降,與實驗觀察有較好的一致性。

圖4 不同空化模型預測附著空穴長度隨時間的變化過程(σ＝0.80,α＝8°,Re＝7×105)[62]Fig.4 Evolution of attached cavity length predicted by different cavitation models(σ＝0.80,α＝8°,Re＝7×105)[62]

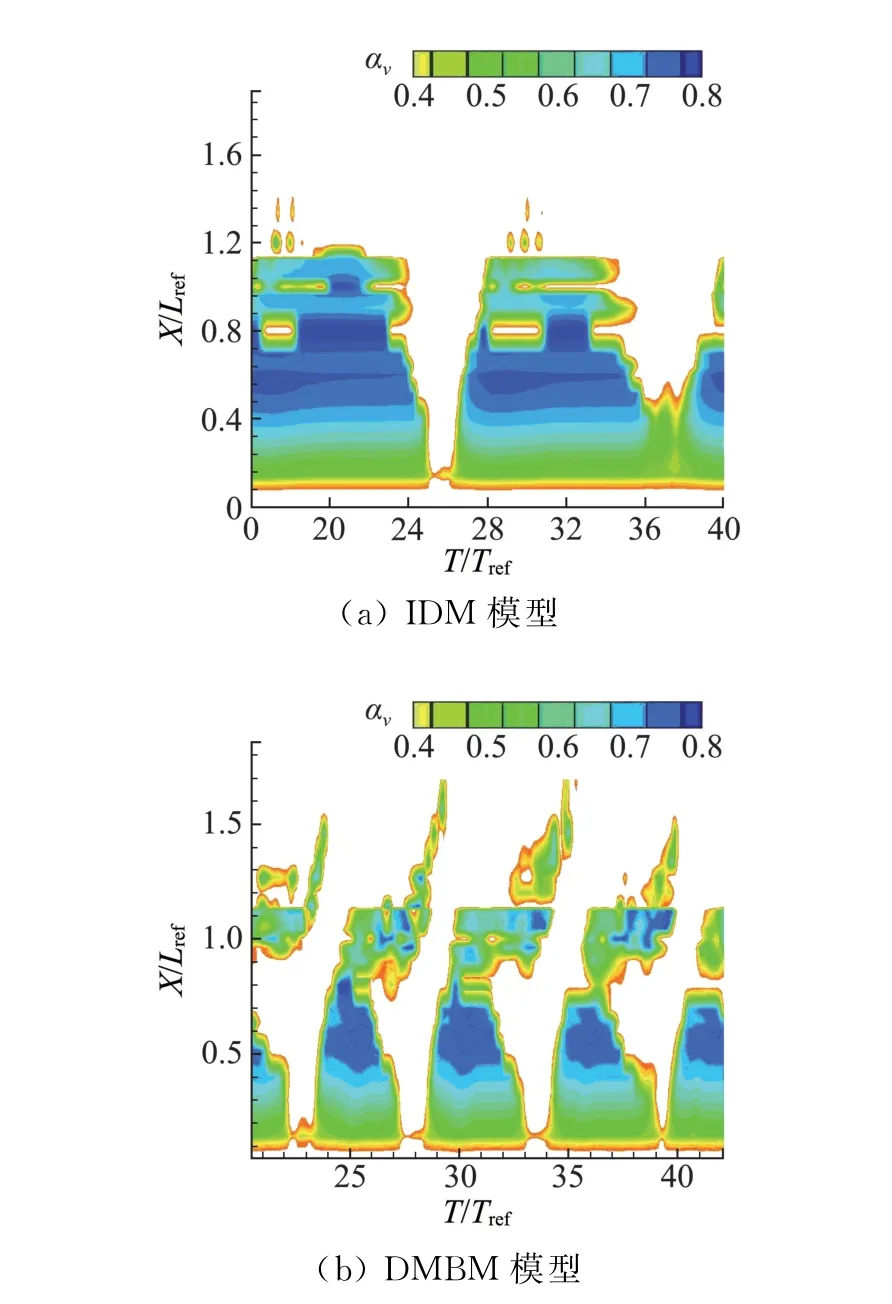
圖5 不同空化模型預測得到的云狀空化水汽含量時空變化云圖(σ＝0.80,α＝8°,Re＝7×105)[62]Fig.5 Space-time evolution of water vapor volume fraction predicted by different cavitation models(σ＝0.80,α＝8°,Re＝7×105)[62]

空化流動幾乎包含了所有復雜的流動現象,尤其是云狀空泡團發展過程的強烈不穩定行為,往往與流場旋渦結構的運動密切相關。因此,對湍流的數值模擬是建立非定常空化流動數值計算方法的關鍵。目前對湍流的數值模擬主要有雷諾時均化湍流模型(Reynolds-Averaged Navier-Stokes,RANS)和大渦模擬(Large Eddy Simulations,LES)。

長期以來,建立在雷諾時均化Navier-Stokes方程(RANS)基礎上的數值模擬方法是空化流動數值模擬的主要選擇,湍流模型在很大程度上影響著對空化流動的精確預測。Launder和Spalding提出的標準k-ε 模型[63]定義了渦黏系數與湍動能和湍動能耗散的關系,其穩定性、經濟性、適用性以及一定的精度使之在目前的工業流動和熱傳遞模擬中得到廣泛的應用,但是該模型在處理多重湍流尺度決定的動力流動結構方面的缺陷使其在非定常流動計算中的應用受到了很大的限制。為了解決標準RANS模型在空化流動中對黏性系數過度預測的問題,Kinzel[64]采用DES模型對繞三維軸對稱回轉體的空化繞流現象進行了模擬,并與采用標準RANS模型得到的結果進行對比,研究表明DES模型對于空穴區域內的反向射流現象及大尺度空泡團的整體脫落有較好的模擬。Johansen等[65]、Wu 等[66]、黃彪等[67]采用一種基于標準k-ε 模型的濾波器湍流模型(Filter-based Model,FBM)對繞Clark-Y 型水翼云狀空化流動進行了數值計算,更準確地模擬出了云狀空穴形態與空化區尾部渦團交替脫落的非定常細節。Yakhot[68]、Coutier-Delgosha[69]、Zhou和Wang[70]、Yang等[39]、李向賓等[71]引入水和水蒸汽混合密度函數對RANS模型進行了修正,提高了模型預測精度。黃彪等[72-73]基于對非定常空化的流動特性的認識,針對非定常空化流動的湍流多尺度和多相局部可壓縮特性,提出了一種基于混合密度分域的混合湍流模型(FBDCM),綜合考慮了空化流動的湍流多尺度效應和多相流動特性,實現了對附著空穴生長過程等流動細節的準確預測。圖6給出了采用FBDCM 數值計算獲得非定常云狀空泡形成、發展、脫落與潰滅過程及其與實驗結果的對比。綜合實驗與數值計算結果表明,伴隨著空泡團的脫落,在空穴尾部形成U 型的空泡渦腔,隨著時間的推移,空泡腔逐漸向下游移動,隨后U 型空泡渦腔從其頭部斷裂,形成兩個較小的空泡腔結構,渦腔兩側逐漸潰滅、消逝。數值計算結果較好地描述了空穴尾部U 型空泡渦腔的非定常變化過程,從流場的壓力分布云圖可以看出,空腔頭部瞬時的高壓是造成其斷裂的主要原因。Huang等[74]基于上述結果進一步通過分析渦輸運方程發現了空泡與渦結構之間的強相關性。通過分析渦輸運方程,結合實驗結果與數值結果,發現空泡與渦結構之間的強相關性。回射流與空泡之間的相互作用可以引起氣液兩相的變化,增加壁面附近的渦量。

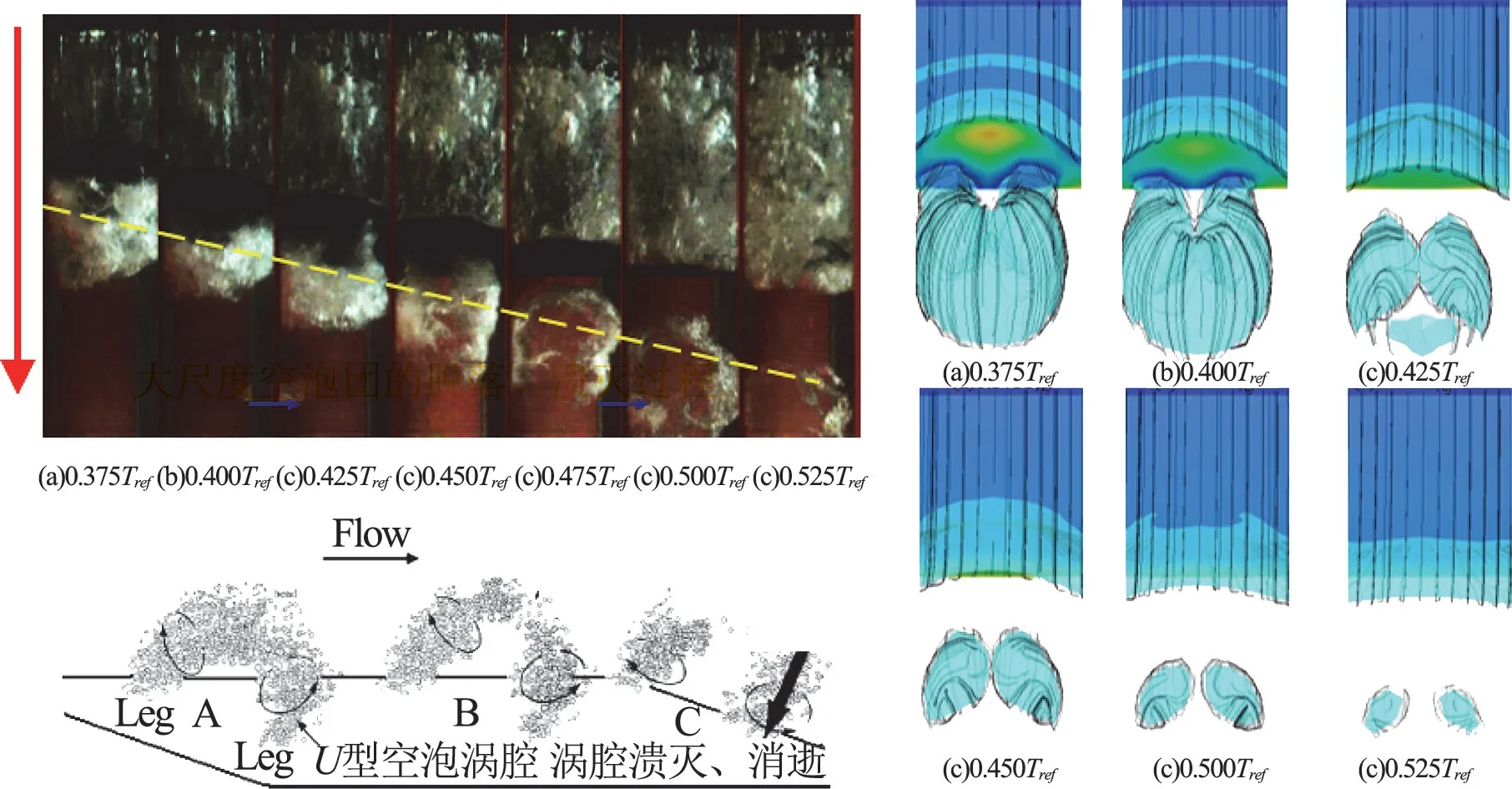
圖6 實驗與數值預測非定常云狀空泡形成、發展、脫落與潰滅過程[18]Fig.6 Formation,development,shedding and collapse process of unsteady cloud cavitation[18]

研究表明,非定常空化流動中存在多尺度旋渦結構,RANS模型過高預估的湍流黏性會抑制空泡旋渦的脫落[75],從而影響空泡流動預測的精確性。為了實現高雷諾數湍流流場旋渦結構的精細捕捉,大渦模擬方法[76]基于濾波概念嘗試捕捉流場中大部分湍流尺度,即對大尺度湍流進行直接計算,對可視為同向且均一的亞網格尺度湍流進行模化(Sub-Grid Scale,SGS),從而能夠較好地預測各種空化湍流渦的運動及其造成的不穩定性和周期性。LES方法也被認為是最有可能提高空化湍流流動工程計算精度,從而推動計算空化流體動力學向精確定量預測技術轉變的方法[77]。Wang和Ostoja-Starzewski[48]采用大渦模擬方法計算了不同迎角下繞NACA0015翼型空化流動,研究結果表明,大渦模擬方法能夠捕捉到云狀空泡潰滅及相關的不穩定性特征。Ji[78]等通過研究表明與無空化流動相比,空化的發生和潰滅使數值計算變得更加復雜,采用大渦模擬方法能夠較好地獲得非定常空化發展過程中的空泡演變規律及其與湍流旋渦結構的相互作用,并與實驗結果吻合較好。Gnanaskandan和Mahesh[77]采用大渦模擬LES 方法研究了雷諾數分別為Re＝200和Re＝3900時繞圓柱空化流動。研究發現空化會對圓柱表面壓力、邊界層和載荷均產生影響。空化的產生有效地降低了尾跡區的雷諾數,抑制了湍流并推遲了三維旋渦結構的破碎。Wang 等[30]采用LES 方法計算了雷諾數Re＝6.7×104,通氣率Qv＝0.0866時繞鈍體模型的空化流場結構,如圖7所示。數值計算結果較好地模擬出展向卡門渦街結構。由于流體的黏性剪切作用,剪切層卷起形成旋渦,上、下剪切層形成的渦對相互卷吸和耦合,最終導致旋渦脫落,形成兩列旋轉方向相反、交叉排列且相對穩定的渦街。在文獻[3]中也表明,在湍流剪切流中,空泡的初生階段主要受單相流中的流動結構控制。

圖7 通氣空化旋渦脫落形態(Qv＝0.0866,Re ＝6.7×104)[30]Fig.7 Evolution of ventilated cavitating vortex structures(Qv＝0.0866,Re ＝6.7×104)[30]

近年來,隨著計算機軟硬件技術的發展,直接數值模擬(Direct Numerical Simulation,DNS)也在低雷諾數湍流的研究中發揮了作用。直接數值模擬(DNS)不需要建立湍流模型[79-80],直接求解Navier-Stokes方程,幾乎能夠捕捉到湍流場中包含的所有尺度旋渦結構,即從大尺度到Kolmogorov尺度的渦結構。由于湍流場中大尺度渦與小尺度渦之間的比值,隨著雷諾數的增加而變大,在高雷諾數時,湍流尺度的譜域較寬,要捕捉湍流流場中所有尺度的旋渦結構,需要很高的時間和空間分辨率[81],網格數要達到Re9/4的量級,才能滿足直接數值模擬的計算要求[82],從而限制了DNS方法在工程上的運用。目前關于直接數值模擬的應用仍局限于相對較低的雷諾數。Rogers和Moin[83]基于DNS分析了均勻剪切層湍流內部旋渦結構,表明展向渦的卷起是“發卡”渦結構形成的主要原因,與壁面湍流的非均勻效應關系不大。Rodriguez等[84]通過直接數值模擬對雷諾數Re＝3700的繞球體尾跡區旋渦結構進行了精細地捕捉,并對一階和二階統計量進行了分析。直接數值模擬方法在低雷諾數下單相湍流的精細預測方面發揮了其它方法不能替代的作用。王志英等[85]采用DNS方法精確地分析了繞圓柱湍流尾跡區的通氣空泡與湍流的相互作用。

數值模擬方法在解決空化與湍流相互作用這一問題中仍然面臨許多困難與挑戰。空化非定常過程包含了從微米尺度的單個空泡到與流動幾何尺度相當的多物理尺度的復雜流動現象,其中微米尺度的單個空泡或單個空泡聚集而成的空泡團的潰滅過程是空化現象的核心問題。在空化模型方面,現有的空化模型大多數基于單泡動力學或是平衡態模型。如果能將空泡群動力學和宏觀空化流動模型有效結合起來,建立多尺度空化模型,將有利于更準確地描述空化區內部結構及其對宏觀流場的影響,為分析空泡團潰滅產生的沖擊壓力波的傳播對流動的影響提供手段。

2 空化流激振動特性的研究現狀

隨著水力機械、船舶與海洋工程等領域的不斷發展,人們對水中結構安全性能的要求也不斷提高,流激振動及水動彈性問題也逐漸引起人們的關注。對于流激振動現象的早期認識源于機翼及葉片的氣動彈性問題。早期的學者基于線性勢流理論,利用解析方法對繞二維彈性機翼流動的空氣動力特性進行了分析研究。Theodorsen[86]建立的非定常氣動力理論奠定了氣動彈性不穩定研究的基礎。Sear[87],Garrick[88]等基于線性勢流理論對二維機翼均勻來流小幅簡諧振動條件下的氣動力進行了理論分析。Thomas等[89]基于單自由度模型研究了非線性氣動力作用對機翼顫振、氣彈穩定性等的影響。Edwardshe和Wieseman[90]應用有限元分析方法與偶極子網格法對機翼靜發散與顫振不穩定性進行了分析。然而與經典氣動彈性問題不同的是,在水動力學相關領域中,復雜水力環境下的流固耦合效應會導致系統動力特性明顯改變,并與流速、壓力、湍動能、渦湍黏性等流動參數的變化緊密關聯,隨流態變化而異,這顯著加劇了流激振動問題研究的理論難度。因此,在當前的理論條件下,處理流激振動問題仍然是基于模型試驗或是數值模擬進行。

2.1 空化流激振動的試驗研究

國內外學者對水中繞流物體的流激振動特性及其影響因素進行了大量的實驗研究工作。張效慈等[91]采用顏料示蹤法進行實驗觀測,發現水翼結構近壁區域流線呈霧狀擴散,表明結構振動對流場影響顯著。王文全等[92]基于粒子圖像測速系統和加速度傳感器研究了方柱繞流后彈性薄板的流激振動特性,揭示了彈性薄板周圍流場時空演化與結構振動運動的強非線性耦合作用。

在空化載荷作用下,水中結構流激振動及水彈性問題更加復雜,尤其是大尺度云狀空穴的潰滅導致的壓力脈動會引起結構強烈振動、劇烈的噪聲和結構空蝕等危害[93-95]。隨著實驗設備和技術手段的發展,流激振動問題的實驗研究不斷深入。Kubota等[51]測量了非定常空化流動時的速度和壓力脈動,揭示了壓力脈動和空化發展的聯系。So等[96]采用激光多普勒測振儀和激光多普勒測速計對繞彈性圓柱體非定常流動的結構動力學特性及尾跡流動特征進行了研究,分別測得結構的彎曲變形量和尾跡區域的速度分布,結果表明由于圓柱體的振動,流場湍流強度顯著增強。Glio等[97]基于高頻壓力傳感器測量了葉輪流道內的壓力脈動,分析了壓力脈動作用下的葉輪振動特性。Ducoin等[98-99]采用微型壓力傳感器、激光多普勒測速計、激光多普勒測振儀等設備測量了水翼表面的壓力、邊界層速度分布以及水翼的振動速度,研究了流場層流向湍流轉捩分離和非定常旋渦脫落引起的水翼結構振動響應,結果表明,振動特性與渦脫落頻率及結構固有頻率密切相關。De La Torre等[100]測量了水翼在空化條件下的固有頻率,揭示了附加質量對流固耦合系統的影響。Lelong[101]測量了水翼的變形、振動、應力應變及空化特征,并發現了空化頻率和彎曲頻率的鎖頻現象。水翼結構在不同空化階段呈現出不同的振動特點。水翼結構的流激振動頻率隨著空化數的降低而減小,最大振動速度在初生空化和片狀空化階段保持在較低水平,受云狀空化階段強烈的非定常特性影響,最大振動速度和位移大幅增加,在超空化階段由于超空泡的包裹效應,最大振動速度和位移顯著下降。如圖8所示,不同空化階段下,隨著空化數的減小,繞水翼空化流動誘導的主要流激振動頻率分別為165 Hz、90 Hz和18 Hz。結合不同空化階段下的空穴形態可知,流激振動頻率與空泡脫落頻率基本一致,且這一頻率在無空化的單向流動中不存在。這說明,繞水翼非定常空化流動中,空泡的非定常脫落是導致水翼結構振動的主要因素,且隨著空化數的減小,空化發展周期增大,從而導致空泡脫落頻率和水翼結構的流激振動頻率減小。

圖8 不同空化階段的水翼結構振動頻譜[102]Fig.8 Structural vibration spectrum of for typical cavitation regimes[102]

綜合空化流動實驗研究的現狀與發展趨勢,應用多場同步測量方法研究空化流動是實驗技術的重要發展方向。Chen等[103]建立了一套基于空化水洞的空化流動多場同步測量系統,利用高速攝像機和動態壓力傳感器實現了收縮-擴張管內不同空化階段的動態空穴形態和流道壁面壓力脈動的同步采集,揭示了空穴形態演變規律與流體動力特性的相互關系,結果表明空化流場的壓力波動幅度明顯增大,研究進一步捕捉到了壓力脈動的主導頻率。Aktas等[104]進行高速攝像、壓力脈動和振動噪聲同步測量,由此發展了空化動力學分析方法,并進一步解釋了空化誘導噪聲機理。Ma等[105]通過同步觀測不同碳纖維復合材料壁面附近空泡潰滅過程的流場形態演化過程,以及平板壁面變形特征,深入分析碳纖維復合材料壁面附近空泡發展過程的流動特性。對于空化流激振動,云狀空化流場結構的瞬態演變是影響結構動態振動響應特性的主要因素。圖9給出了采用高速攝像機與激光多普勒測振系統同步觀測獲得的水翼空化非定常演變情況及其誘導振動速度。綜合流場形態與結構振動的同步分析發現,空泡的非定常發展過程引起結構的振動,反向射流引起的云狀空泡團斷裂導致結構振動速度達到波動峰值,空泡的周期性脫落導致結構的振動速度發生大幅周期性變化。

2.2 空化流激振動的數值模擬研究

由于其相關的實驗測試對測量技術、成本的要求較高,同時往往會受到測試條件與環境的諸多干擾,針對流固耦合振動機理開展的實驗研究具有一定的局限性。隨著計算機技術的發展,數值計算方法逐漸成為研究流固耦合問題的主要手段。鄭小波等[106]對軸流式葉片進行了振動特性分析,計算了葉片在空氣中和水中的固有頻率與振型。王福軍等[107]應用耦合界面模型研究了國內某大型水電站安裝的混流水輪機轉輪在不穩定壓力場與結構場耦合作用下的動態響應。Munch 等[108]基于大量實驗與數值計算結果提出了一種繞水翼非定常流動的水彈性響應預測模型,通過建立流體慣性、阻尼和剛度系數的經驗表達式,準確預測了流固耦合作用下的水動力系數。

圖9 云狀空化條件下瞬態空穴形態及其誘導振動速度隨時間的演化規律[41]Fig.9 Evolution of cavity patterns and induced vibration velocity[41]

流固耦合問題的求解需要同時考慮流場和結構場的求解及其耦合。對于流固耦合場的求解算法,一般包括消除變量法、整體求解法和分步求解法。由于消除變量法只適用于線性問題中,且在數值方法計算時容易出現困難,因而應用較少。

整體求解法(Monolithic Approach)也稱完全耦合法(Fully Coupled,FC),對流體和結構建立統一的耦合方程,在一個時間步內對流體域和固體域中所有的未知量進行同時求解,如圖10所示。基于此建立的流場與結構場具有強烈的相關性,能精確求解出流體和結構的響應,完全消除求解過程中的時間延遲,且數值收斂性較好,計算精確度較高。Ryzhakov等[109]利用完全耦合法基于拉格朗日體系建立了流場和結構場控制方程,對水流沖擊彈性平板和注水氣球彈性變形等算例進行了分析研究,結果表明完全耦合法能精確求解流體與結構的動態響應,且數值收斂性較好。Michler[110]針對活塞與流體相互作用的一維模型問題,從算法穩定性、計算精度和計算效率等方面對比了不同流固耦合算法在流固耦合問題求解中的應用情況,結果表明完全耦合法無條件穩定且計算精確度相對較高。吳欽等[111]基于完全耦合算法對繞NACA009水翼流固耦合特性進行了數值模擬研究,揭示了流體與結構的慣性作用對水彈性響應有較大影響。然而對于復雜的流固耦合系統,流固耦合方程的理論推導過程相當復雜,求解難度較大,現有的流體和結構計算軟件均無法實現,因此其在工程領域的適用性存在一定局限。

圖10 完全耦合算法示意圖Fig.10 Fully coupled algorithm schematic diagram

分步求解法(Partitioned Approach)分別對流場和結構場選擇合適的數值算法進行獨立求解,流固耦合界面數據通過反復迭代求解并傳遞直至獲得收斂解。其中,分步求解法按照耦合的緊密程度,可分為松耦合算法(Loosely Coupled,LC)和緊耦合算法(Tightly Coupled,TC),如圖11和圖12所示。松耦合算法是在流體和固體各自的求解域內,用各自的求解器分別獨立進行求解,在每個預定的計算時間步內進行流體域和固體域的數據交換。在松耦合算法的基礎上,緊耦合算法在每一時間步中引入子迭代步,在每個子迭代步內交叉求解流動控制方程和結構動力學方程,并通過流固耦合界面進行數據傳遞。緊耦合算法相對于松耦合算法,較好地解決了流場與結構場求解時間延遲問題,子迭代過程中多次的數據交換保證了流場、結構場及流固耦合界面上合理的收斂精度,從而具有更高的計算精度。同時,緊耦合算法相對于完全耦合算法,在求解器、計算模型、網格尺度上都更加靈活。Ducoin等[112]利用松弛耦合分步求解算法研究了繞二維彈性水翼黏性流動的水彈性響應和結構穩定性,結果表明流場作用下,彈性水翼發生繞彈性軸順時針方向的扭轉變形,從而導致有效迎角增大,同時結構的變形加速了流場轉捩和失速現象的發生,導致流場的非線性特性顯著。Lee等[113]證實了緊耦合算法對研究彈性翼的渦激振動特性的可行性。

圖11 松耦合算法示意圖Fig.11 Loosely coupled algorithm schematic diagram

圖12 緊耦合算法示意圖Fig.12 Tightly coupled algorithm schematic diagram

表1綜合對比了上述流固耦合算法在水動力學研究中的應用情況。大量研究表明,分步求解法(LC算法、TC 算法等)的優點是容易實施,通過交互程序即可實現結構求解器和流體求解器之間的數據交換,從而實現分步求解。其中,松耦合算法不能保證計算過程中流場與結構場的能量平衡,且計算穩定性受流固密度比等模型參數和計算時間步等計算參數的影響,通過在松耦合求解算法中引入子迭代過程,緊耦合算法能在一定程度上保證流場與結構場的能量平衡,并提高算法的收斂性和穩定性,但均沒有考慮水的附加質量、阻尼等對水翼結構的運動和變形的影響,無法解決附加質量效應帶來的數值收斂問題[114-115]。

為了進一步研究附加質量效應對結構流激振動特性的影響,Young等[118]、Wu等[119]發展了一種混合耦合算法,相比于其他分步耦合算法,混合耦合算法收斂性和數值穩定性更好。圖13給出了采用不同流固耦合算法對單自由度水翼結構動力學方程進行求解所得扭轉變形角度隨時間的演變情況。通過改變時間步長、激勵頻率等參數,對比不同耦合算法在求解過程中的數值穩定性發現,完全耦合算法(FC)在不同工況下的計算均無條件收斂,具有較好的數值穩定性。當d t＝T/480 時,松耦合(LC)、緊耦合(TC)和混合耦合算法(HC)均與完全耦合算法計算結果一致;當d t＝T/120時,松耦合算法與最大迭代步數為1的混合耦合算法的計算結果均發散,隨著迭代步數的增大,緊耦合算法和混合耦合算法均較好地獲得收斂數值解,其中松耦合算法可看作最大迭代步數為1的緊耦合算法。這主要是因為,松耦合算法根據上一時間步流固界面位移計算得來的流體對結構的作用力與當前流場實際作用力存在一定誤差,不能保證計算過程中流場與結構場的能量平衡,計算穩定性受計算時間步等計算參數的影響較大。同時,對于不同固體結構屬性,在不同頻率的激勵條件,松耦合算法和緊耦合算法均發生明顯的發散現象,這主要是因為松耦合和緊耦合算法均忽略了流體的附加質量效應,從而增大了數值計算誤差。尤其對于流固相對密度較小的流固耦合問題,附加質量效應是造成數值不穩定性和降低計算精度的重要因素,數值計算穩定性受流固密度比等模型參數和計算時間步等計算參數的影響。混合耦合算法通過引入Theodorsen模型有效考慮了流體對結構的附加質量效應,可以減少對結構位移的過度預測,提高數值求解的穩定性和精確性。

表1 流固耦合方法研究Table 1 Fluid structure coupling algorithms

圖13 不同流固耦合算法穩定性對比Fig.13 Comparison of stability of different fluid-structure interaction algorithm

為了進一步研究不同材料水翼的非定常空化流激振動特性,Wu等[119-120]研究了繞彈性水翼非定常空化流動及其誘導振動特性。結合圖14和圖15所示,水動力隨時間的變化主要分為三個階段:伴隨著附著空穴的發展,彎曲和扭轉變形隨著升力系數增大而增大;由于空穴的潰滅和與渦結構強烈的相互作用,水翼的彎曲和扭轉變形產生大幅波動;隨著空穴脫落和流場渦結構向水翼下游移動,水翼的彎曲、扭轉變形與升力系數同步下降。

圖14 彈性水翼彎曲、扭轉變形以及升力系數隨時間的演變過程Fig.14 The evolution of bending,torsional deformation and lift coefficient of flexible hydrofoil

圖15 繞剛性和彈性水翼非定常空化形態隨時間的演變過程Fig.15 Evolution of unsteady cavitation around rigid and flexible hydrofoils

3 研究展望

通過對近年來國內外在非定常空化流動及其誘導振動特性的實驗和數值計算方面研究工作的總結,認為在該領域仍有諸多工作值得進一步地探究:

1)已有研究表明,非定常空化流動及其誘導振動特性涉及流場速度、壓力、相變等與結構場振動位移、速度、加速度等的相互作用,現有的單一試驗技術已經發展較為成熟,但單一試驗測量結果不能較好地反映各瞬態物理場的相互作用。為了更好地研究空化流動及其誘導振動特性,針對空化流動的多場耦合特性,有必要建立集高速全流場顯示技術、瞬態粒子測速技術、動態壓力測試技術和結構瞬態振動速度、結構振動位移等為一體的多場同步測量試驗平臺,開發數據同步采集和后處理系統,解決瞬態空化形態觀測、非接觸速度測量、脈動壓力測量、精確振動速度測量等問題,實現非定常空化特性與空化流激振動特性的同步觀測與分析。

2)隨著互聯網、大數據、云計算等技術的不斷發展,機器學習與計算流體動力學(CFD)的結合已成為非定常空化流動和空化流激振動數值模擬方法發展的重要方向。Li等[121]結合深度學習理論,發展了一種基于長短時記憶神經網絡的非定常氣動力模型,該模型能夠更好地體現氣動力非定常特征引起的短時和長時時滯效應。Zhang等[122]采用卷積神經網絡建立了一種基于DNS數值計算結果的RANS數值計算結果優化算法,結果大大提高了數值計算效率和精確度。盡管機器學習在非定常空化流動試驗與數值計算領域的研究尚未起步,但已有研究充分表明,機器學習為試驗數據分析與數值模擬方法的進一步發展提供了可能,也必將成為今后發展的重要方向。

3)空化流動幾乎包含了所有復雜的流動現象,尤其是云狀空泡團發展過程的強烈不穩定行為是影響結構動態振動響應特性的主要因素。目前空化流激振動的研究主要關注流場空泡形態演變及其相應壓力脈動和結構振動分析[123],對于流動與結構振動穩定性機制的研究尚不深入,尤其是針對壓力波導致的空泡失穩機制。Arndt 等[26]首 先 觀 察 到NACA0015水翼的兩種狀態:當σ/2α＞4時,回射流對空泡失穩起主要作用;當σ/2α＜4時,流動主要受激波影響。Leroux等[33]觀察到了NACA66水翼的準穩定部分空泡和云狀空化現象,并基于參數σ/2(α－α0)得到了類似的結論。吳欽等基于試驗觀察到了類似現象,并結合結構振動測量結果發現,與回射流導致的大尺度云狀空泡團脫落誘導結構振動特性相比,大尺度云狀空泡團的潰滅沖擊波及其引起的附著空泡二次潰滅導致結構振動顯著加劇。王暢暢等[124]進一步采用可壓縮數值計算方法分析了上述不同云狀空泡脫落機制。對于上述不同空泡脫落機制,國內外學者的說法尚未統一,通過X 射線等技術深入分析空化區域內的回射流與沖擊波演化特征,并結合結構精細化振動測試技術,對流動參數進行系統的歸納、分析,建立更完善的空化流激振動穩定性機制分析,是今后進一步研究空化流動機理、理解非定常空化流激振動特性的重要關注點。