表面熱流辨識結果的誤差分析與估計

錢煒祺,周 宇,*,邵元培

(1.空氣動力學國家重點實驗室,綿陽 621000;2.中國空氣動力研究與發展中心 計算空氣動力研究所,綿陽 621000)

0 引 言

表面熱流辨識是通過材料邊界或內部的溫度測量值來反演表面熱流,是一類典型的熱傳導逆問題,在航空航天、冶金制造等領域有廣泛的應用。表面熱流辨識是數學上的不適定問題,不滿足解的穩定性,也就是說即使測點溫度存在較小測量白噪聲也可能導致解的“爆破”;具體來說,在頻域,表面熱流的辨識誤差在白噪聲的影響下隨著頻率的升高逼近無界。這給辨識精度估計帶來了難度,而在工程實際的測熱系統設計時,希望能夠在對熱環境有大致預測的情況下對其辨識結果誤差給出較為準確的估計,進而根據辨識結果精度要求來確定傳感器的測量位置和測量精度。文獻[1]針對這一問題進行了探討,結果顯示,辨識結果誤差不僅與防熱材料物性參數、測量點位置、測量噪聲形式、測量噪聲大小有關,而且還與表面熱流本身的頻域特性有關。將傅立葉數作為相似參數,可以對辨識結果誤差進行初步的分析。但是這一結果給出的主要還是定性分析的結論,在定量評估上還存在不足。因此,本文工作是文獻[1]的進一步深入探索,首先對給定單一頻率的熱流辨識誤差進行定量分析,然后結合頻域分析方法[2-3]對兩個和多個給定頻率組合情況下的誤差規律進行分析,初步建立熱流辨識誤差的定量分析方法。

1 熱流辨識方法及辨識結果誤差定義

對典型的一維熱傳導問題,采用文獻[1]中的無量綱方法后,傳熱方程可寫為:

初始條件:t＝0:T＝0

其中,xi(i＝1,P)為溫度測點位置;P 為測點數目;為溫度測量值;v(t)為測量噪聲。通常的熱傳導正問題計算是給定熱流Q(t),計算測點的溫度響應,而熱流辨識問題則是根據觀測方程中的測點溫度信息來確定Q(t)。

表面熱流辨識方法主要有順序函數法和共軛梯度法[4-5],本文采用共軛梯度法來對式(1)進行表面熱流辨識,共軛梯度法將辨識問題轉化為求合適的Q(t)使如下目標函數達極小的優化問題:

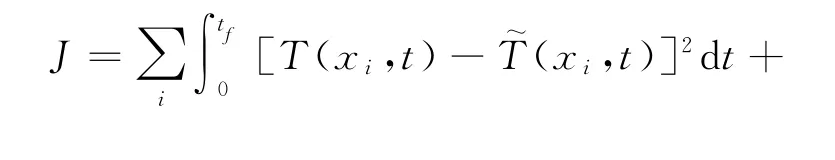
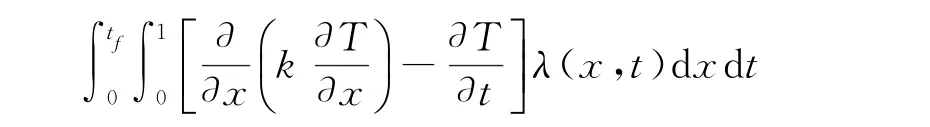
對上式做變分后可以得到伴隨變量滿足的伴隨方程,同時可以得到目標函數對Q 的梯度,然后代入具有“停止準則”的共軛梯度法進行優化計算;“停止準則”是一種迭代正則化方法,可以有效抑制辨識結果的高頻非物理振蕩。具體算法和有效性驗證參見文獻[5,6]。圖1給出了典型算例的辨識結果,此時的表面熱流真值取為頻率f＝2 Hz的正弦函數,即圖1中的“Exact”,測點位于絕熱端x＝1,算例中相應的無量綱量k 為1。“Est.(σ＝0)”表示不考慮測點溫度測量誤差情況下的熱流辨識結果,“Est.(σ＝0.05)”表示在測點溫度疊加標準差σ＝0.05Tmean白噪聲情況下(圖2中的“Exp.(σ＝0.05)”)的熱流辨識結果,Tmean為測點溫度變化平均值。從圖中可以看到,在不考慮測量噪聲和測量噪聲標準差σ＝0.05的情況下,熱流辨識結果和真值都符合;在考慮測量噪聲情況下,根據熱流辨識結果計算出的測點溫度(圖2中“Fitted(σ＝0.05)”)也與測量值符合,表明辨識算法是有效的。

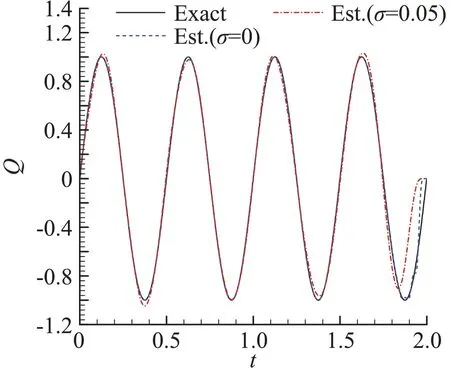
圖1 熱流真值與辨識結果對比Fig.1 Comparison of exact and estimated value of heat flux

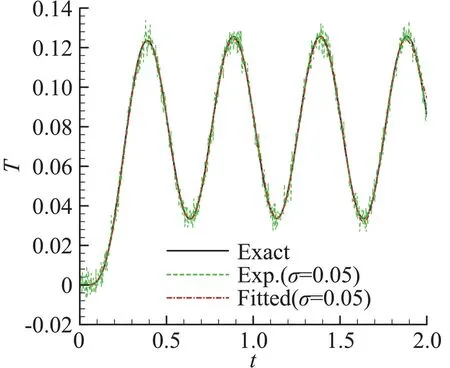
圖2 測點溫度測量值與辨識擬合值對比Fig.2 Comparison of measurement temperature

定義辨識結果與真值之間的相對誤差E 為:

從圖1可以看到,由于傳熱的延遲特性,測點溫度信息對表面熱流尾段值不敏感,導致熱流尾段值與真值存在一定誤差,因而在式(2)計算時只取中間一段來進行分析,即t1＝0.25,t2＝1.25。此外,由文獻[1]分析知,在白噪聲的影響下辨識結果誤差同樣具有一定的隨機性。為克服這一影響,采用如下方法:首先給定相同均值、相同標準差的N 組白噪聲;對疊加這些噪聲后的測量結果分別辨識得出相對誤差值Ei(i＝1,N);然后對這些相對誤差值取平均,將該平均值作為對應這一噪聲標準差水平的平均相對誤差值,記為Em,即

2 給定頻率熱流的辨識結果誤差建模

采用上節方法,首先針對五組不同頻率(f＝1,2,5,8,10 Hz)正弦形式熱流在不同測量噪聲方差σ＝0.01Tmean、0.02Tmean、0.05Tmean、0.1Tmean情況下的辨識結果平均相對誤差進行分析,計算結果如表1所示,圖3中給出了頻率10 Hz情況下不同噪聲水平對應的熱流辨識結果誤差。

圖3 頻率10 Hz不同噪聲水平對應的熱流辨識結果誤差Fig.3 Estimation error for 10 Hz heat flux with reapect to noise standard devition

表1 不同頻率下對應不同噪聲水平的熱流辨識結果與給定值平均誤差EmTable 1 Mean error of estimated heat flux with different frequencies for different noise standard devition levels

接下來以表1中的f 和σ/Tmean為輸入,以Em為輸出,采用Kriging響應面模型[7]進行建模,然后利用該模型對頻率7 Hz熱流在測量噪聲水平σ＝0.02Tmean、0.04Tmean、0.06Tmean、0.1Tmean情況下的辨識結果平均相對誤差值進行預測,并與實際計算結果進行對比。如圖4所示,圖中“Model prediction”為Kriging模型預測結果,“Calculated”為實際計算結果。從圖中可以看到,模型預測結果與實際計算結果符合較好,數值略偏低。

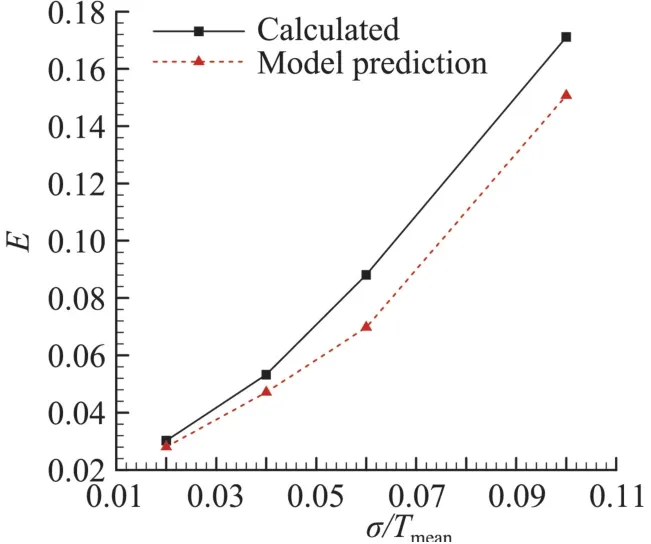
圖4 頻率7 Hz熱流的辨識結果誤差預測結果對比Fig.4 Comparison of calculated and predicted estimation error for 7 Hz heat flux

3 組合頻率熱流的辨識結果誤差估計

對于頻率組合熱流,選取如下幾組熱流進行分析:

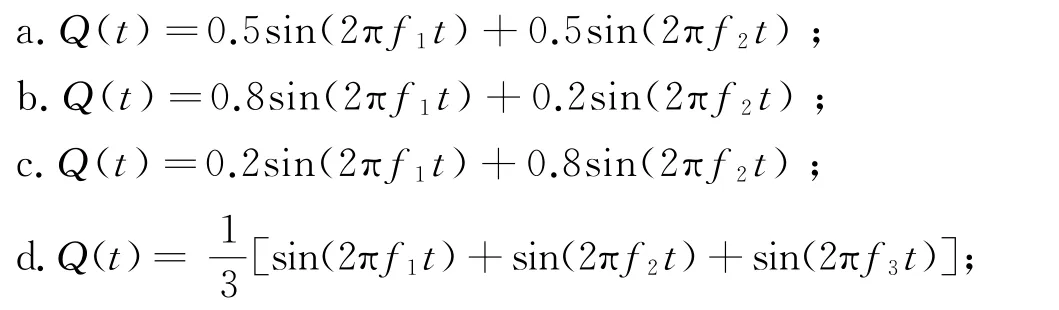
國家提出的“互聯網+”及“大數據”發展戰略，使得傳統的包裝及印刷行業主動或被動地融入其中，為這個古老的加工產業帶來了生機與希望。其優勢主要體現在遙遠的距離被拉近，且囊括了整個加工行業的方方面面。當然，實現“互聯網+”及“大數據”戰略轉型的基礎平臺之一就是網絡搜索引擎的應用。

采用與上一小節相同的方法來計算不同噪聲水平σ＝0.01Tmean、0.02Tmean、0.05Tmean情況下的辨識結果平均相對誤差值。圖5、圖6 給出了σ ＝0.05Tmean情況下熱流b和熱流d的理論值、時域辨識值結果對比和頻域的功率譜對比。從頻域分析結果可以看到,在低頻段,辨識結果與真值較為一致,差異主要體現在高頻分量上。由此可知,對于頻率組合的熱流,低頻分量能在辨識結果得到較好地復現,高頻分量是導致辨識結果與理論值出現差異的主要原因,因此,辨識結果精度可以通過最高頻率熱流分量與測量噪聲之間的對應關系來進行大致估計。選取兩種頻率組合的情況進行分析,以熱流b為例,將其重寫為:

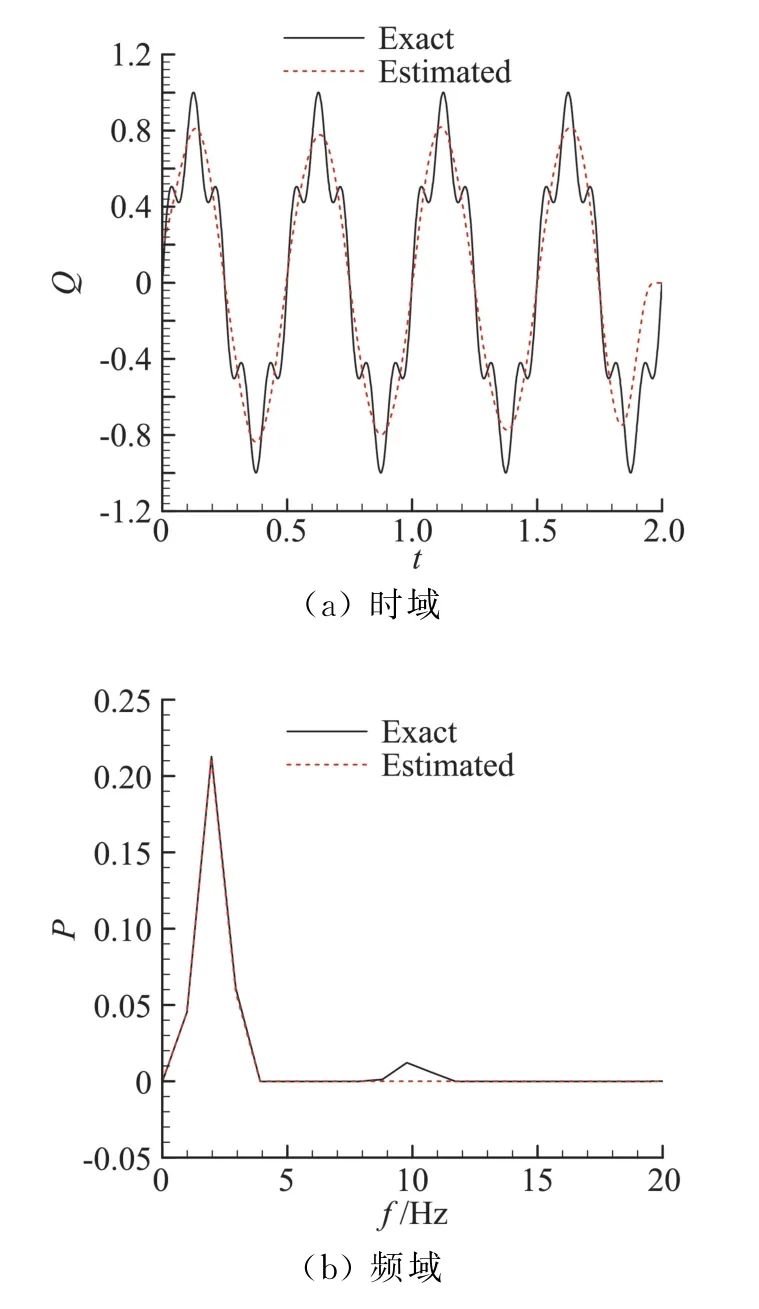
圖5 熱流b理論值、時域辨識值結果和頻域功率譜對比Fig.5 Comparison of exact and estimated value in time and frequency domain for heat flux b

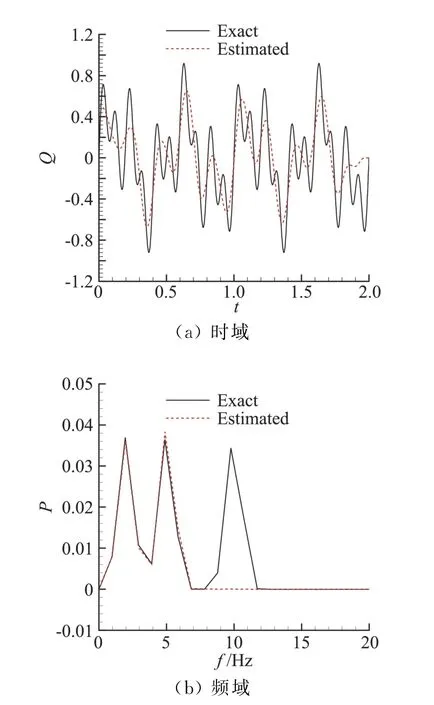
圖6 熱流d理論值、時域辨識值結果和頻域功率譜對比Fig.6 Comparison of exact and estimated value in time and frequency domain for heat flux d

并記Q1和Q2的辨識值為和,則由式(1)的線性可疊加性、函數正交性和式(2)知:

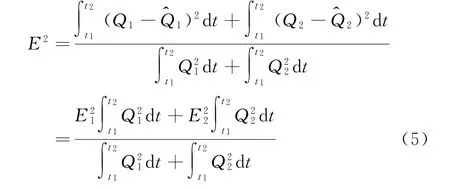
式中E1、E2表示Q1和Q2的辨識結果誤差,由前面分析知,E1≈0,所以上式簡化為:

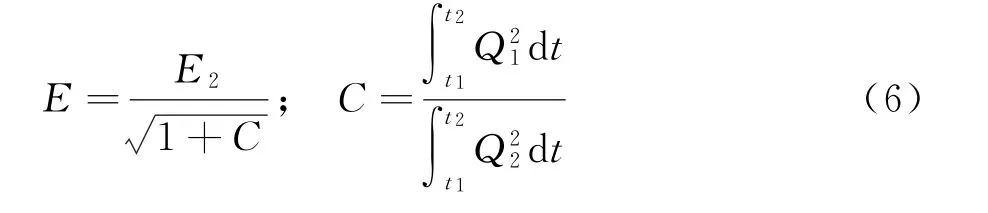
對于Q1和Q2,在時域無法分開,但在頻域可分開,因此,由Parseval(帕塞瓦爾)定理[8]及圖5、圖6可知:

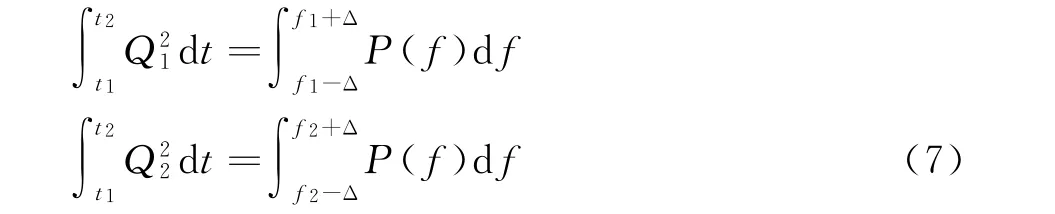
式中Δ為離散變換引起的頻率變化量。則式(6)可另寫為:

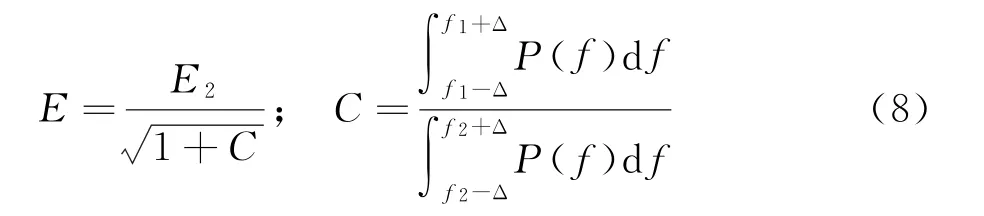
其中C 的物理含義為頻域中高頻分量與低頻分量的能量值對比。

對于N 種頻率組合(N ≥3)的情況,設f1＜f2＜…＜fN,由圖6知,與兩種頻率組合時類似,N 種頻率組合情況下的辨識結果與真值差異主要集中在最高頻分量上,此時的誤差值為:

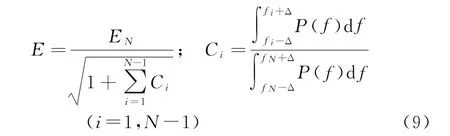
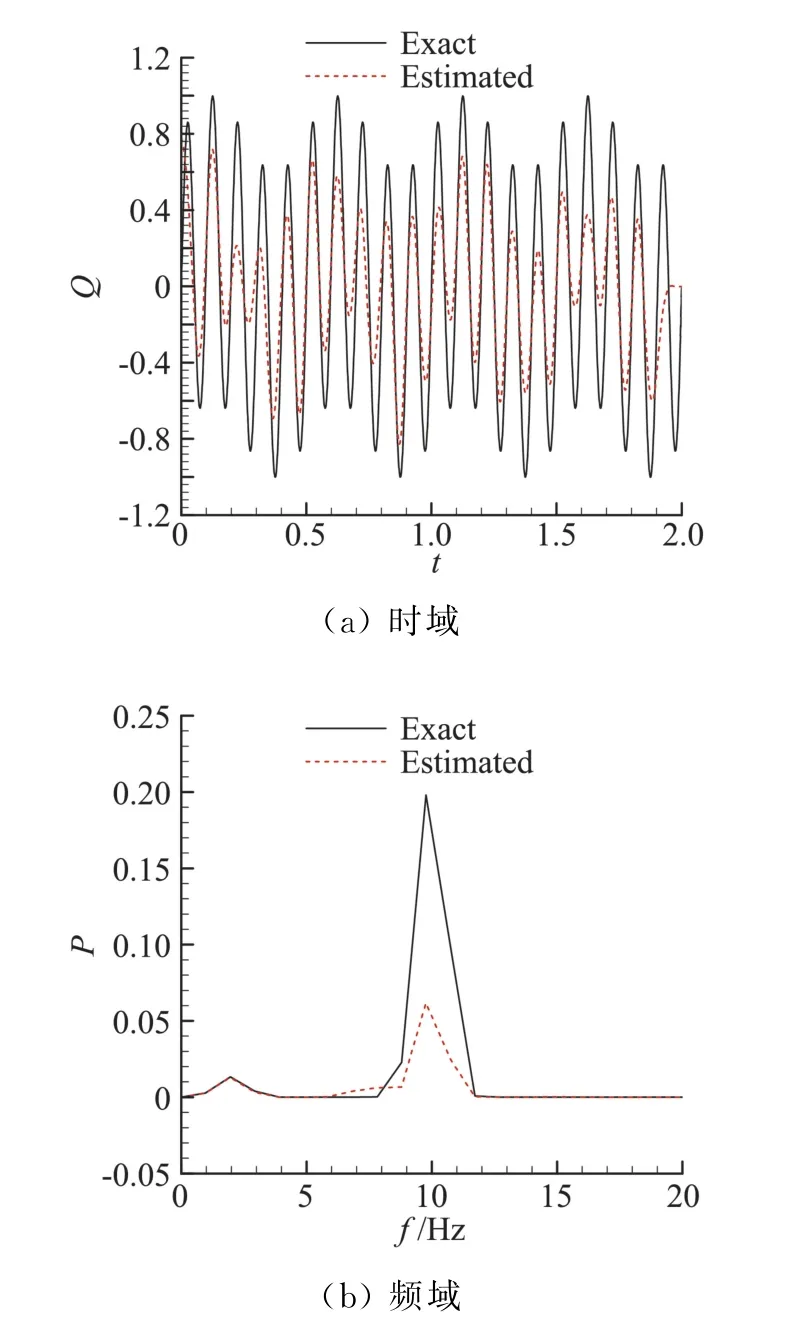
圖7 熱流c理論值、時域辨識值結果和頻域功率譜對比Fig.7 Comparison of exact and estimated value in time and frequency domain for heat flux c

表2也給出了對其余幾組頻率組合情況下采用上述方法的估計結果(表中“估算值”),并與采用式(3)和疊加64組同分布白噪聲的熱流辨識統計平均結果(表中“計算值”)進行了比較,可以看到,兩組結果符合較好。

下面考慮更一般的情況,前面的分析中事先已知了熱流中各分量的頻率、幅值、相位等信息,且熱流均值為0。而在工程實際應用中,這些信息,尤其是熱流的幅值和相位信息不是十分明確,此時的估算方法需更多地借助頻域分析技術。考慮圖8(a)的熱流,對其進行頻譜分析,得出功率譜如圖8(b),由功率譜知該熱流的最大頻率為10 Hz;由于熱流均值不為0,頻譜中包含低頻分量;同時熱流中還包含有頻率為4 Hz的分量。由圖中頻譜曲線積分可知,低頻分量對應的C1≈0.125,4 Hz分量對應的C2≈0.445。接下來還需要確定10 Hz熱流分量的幅值,采用的方法是先濾掉熱流中最大頻率f＝10 Hz的成分,再用原始熱流值減去濾波后的熱流,即得對應頻率10 Hz的熱流分量幅值,如圖9中的“Exact”示,可知,其幅值近似等于0.55。因此,當測量誤差σ＝0.005Tmean時,由前面分析知,該誤差將全部作用到10 Hz分量上,相當于10 Hz分量對應s＝0.005Tmean/(0.55Tm10Hz)情況,Tm10Hz值在之前已計算出Tm10Hz＝0.01457,測點平均溫升Tmean的值由式(1)計算出為Tmean＝0.1414。于是,當σ＝0.005Tmean時,s＝0.0880,在圖3中插值得出E3＝0.3396;代入式(9)可估算出此時對組合熱流的誤差為:

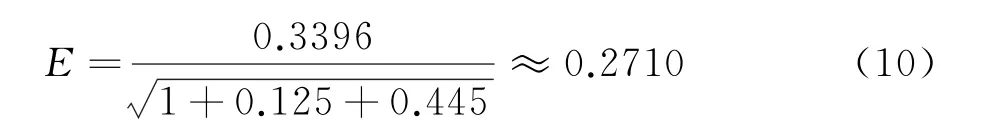
該值與采用式(3)和疊加64組同分布白噪聲的熱流辨識統計平均值0.2576符合較好。進一步考慮測量誤差σ＝0.01Tmean的情況,可采用類似方法計算出s＝0.176,E3＝0.8196,E＝0.6541,與采用式(3)和疊加64組同分布白噪聲的熱流辨識統計平均值0.6176也符合較好,進一步驗證了估計方法的有效性。

綜上所述,對于一多頻率組合熱流,快速分析其辨識結果誤差的具體步驟為:

表2 典型頻率組合熱流的辨識結果平均誤差計算結果與分析預測結果對比Table 2 Comparison of calculated and predicted mean error for estimated multiple-frequency combined heat flux

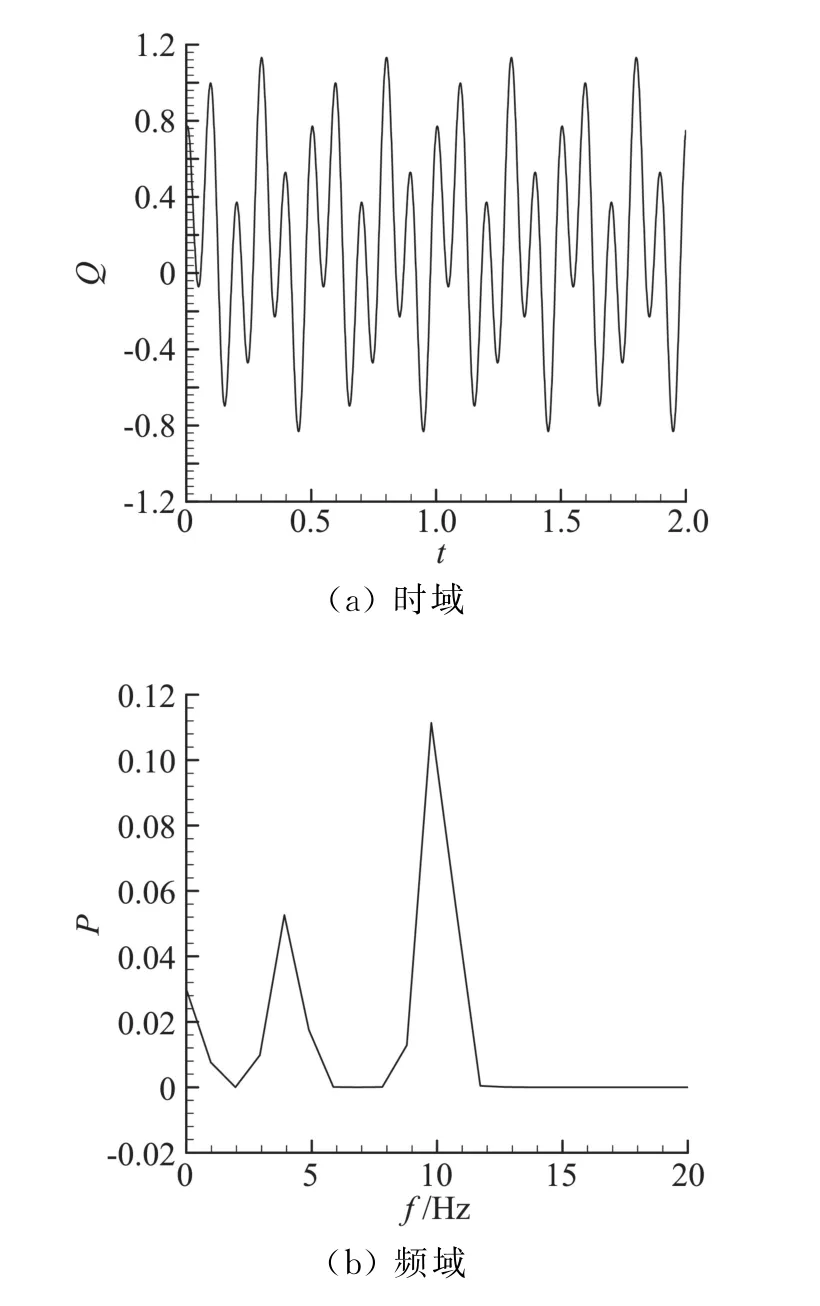
圖8 待分析熱流及其功率譜Fig.8 Exemplified heat flux and its power spectrum

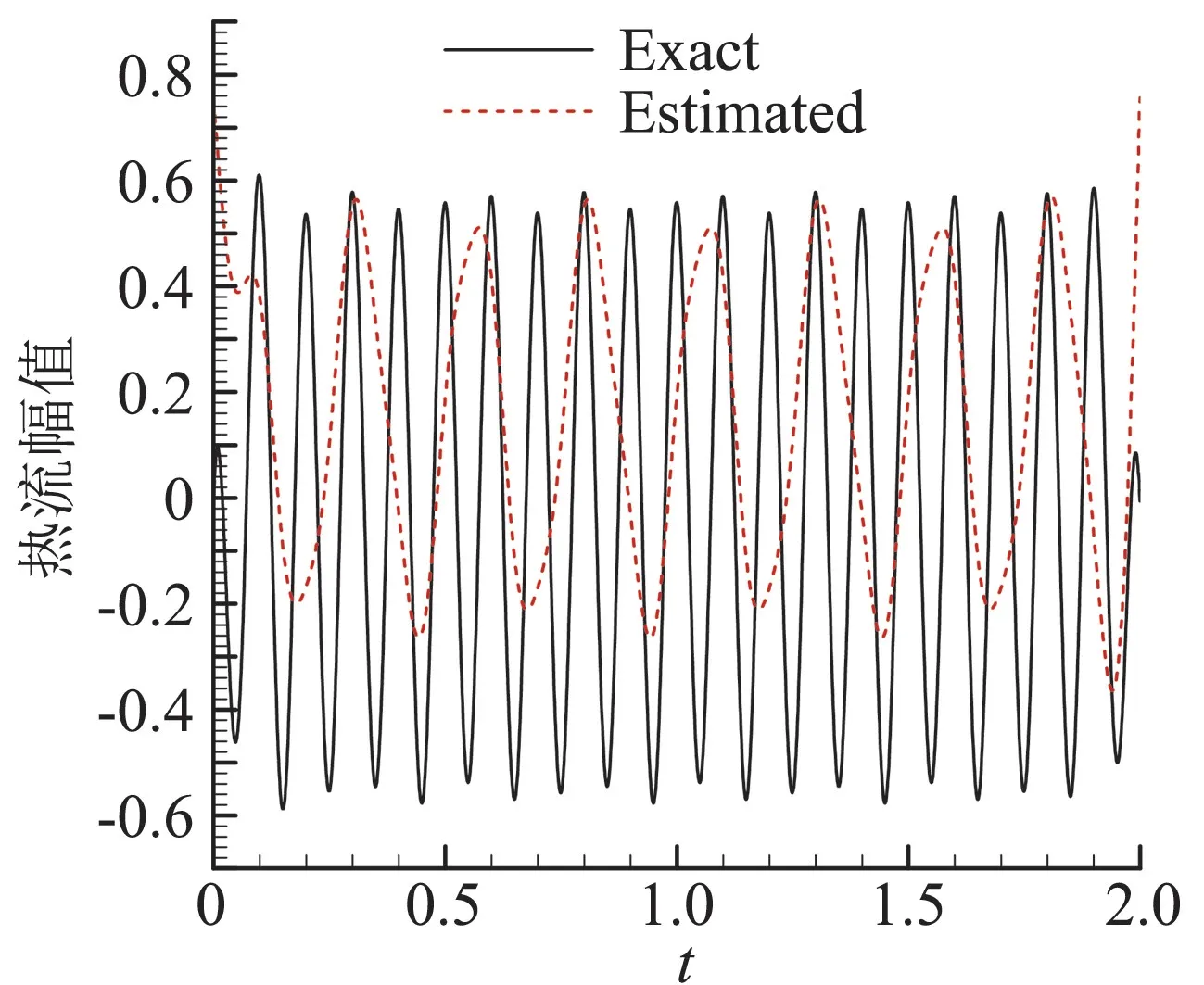
圖9 高頻熱流分量的幅值計算Fig.9 Amplitude calculation of high frequency component of heat flux

1)對待分析的熱流進行頻譜分析,獲知最大頻率以及其余頻率的能量占比;

2)通過濾波計算獲得對應最大頻率熱流分量的振幅AmaxHz;

3)針對最大頻率的周期熱流,計算其測點平均溫升TmaxHz及如圖3所示的“辨識結果誤差～測量誤差”對應關系曲線;

4)由式(1)計算待分析熱流對應的Tmean;

5)根據測量誤差及TmaxHz、Tmean、AmaxHz計算s;

6)由s 值在步驟(3)得出的“辨識結果誤差～測量誤差”關系曲線中插值得EN值;

7)由式(9)估算出待分析熱流的辨識結果誤差E。

4 結 論

本文對表面熱流的辨識誤差進行了深入分析,首先對單一頻率的熱流辨識誤差建立了其與熱流頻率和測量精度之間的響應面模型。然后重點對多個頻率組合情況下的辨識結果誤差進行了定量分析。結果顯示,頻率組合熱流中的低頻分量在辨識結果中能較好地復現,辨識結果誤差可只考慮高頻分量的辨識結果誤差。于是,由辨識誤差定義出發,通過頻譜分析方法可計算出組合熱流中高頻分量的振幅及能量占比,進而建立了組合熱流的辨識誤差的估算方法,并通過多個算例進行了驗證。這一結果一方面有較強的理論意義,揭示了頻率組合熱流與單一頻率熱流辨識誤差之間的內在關聯,深化了對辨識結果時域、頻域特性的認識,并且不僅對傳熱逆問題適用,對其余領域的逆問題誤差分析也有一定的參考價值。另一方面,這一結果在工程上也有實用價值,可減少“暴力”的仿真辨識計算,尤其是形成一些數據庫后甚至可不進行數值計算,直接查表即可對辨識結果誤差進行大致估算。

下一步,方法還需要在以下三個方面進行完善和推廣,一是目前分析中熱流的組合頻率值較為稀疏,在頻域中表現為離散譜,便于開展分析,而對于頻譜范圍較寬、頻譜特性為連續譜的情況,需進一步挖掘辨識計算的“停止準則”與熱流功率譜之間的內在關聯,開展深入研究。二是溫度的采樣頻率對辨識誤差的影響。采樣頻率提高有利于熱流辨識精度的提高,但是采樣頻率與熱流辨識精度的定量關系還需進一步分析。三是目前分析中噪聲形式只考慮了白噪聲形式,對于有色噪聲的情況還需要分析拓展。