曲柄與搖桿擺角的關系

蘇 慧

(保定職技術學院，河北 保定 071000)

平面四桿機構是平面多桿機構，空間多桿機構的基礎，所以對平面四桿機構的設計研究有著很重要的意義。其中曲柄搖桿機構在實際生產中有著廣泛的應用，曲柄搖桿機構的機械特性參數有很多，他們的綜合性能的合理決定著整個機構的運動性能的好壞。這里主要研究曲柄搖桿的擺角ψ。

曲柄搖桿機構按照其壓力角γ的情況可分為兩類：Ⅰ型曲柄搖桿機構的最小傳動角γmin=180°-δm,Ⅱ型曲柄搖桿機構的最小傳動角γmin=δ0。連桿BC和輸出桿CD的最小夾角是δ0，它們的最大夾角是δm，如圖1所示。

圖1 曲柄搖桿機構δ角極值位置

曲柄與搖桿之間不好直接找表達式數值上的關系，這里利用圖解法設計利用圖解法設計θ<90°,θ=90°,θ>90°時的Ⅰ型曲柄搖桿機構，Ⅱ曲柄搖桿機構在任意位置時的圖解特點，分析總結曲柄搖桿機構極位夾角θ與搖桿擺角ψ的關系。

已知要設計曲柄搖桿機構的極位夾角，擺角ψ，搖桿CD長度。D為機架，畫出擺桿的兩個極限位置C1D,C2D即∠C1DC2=ψ,在做以C1C2為弦的圓周角為θ的圓η，延長C1D,C2D，分別交圓η與F,E。在弧C1E,C2F上任意點可作為機架另一鉸點A。用這種方法即可作出規定極位夾角θ，擺角ψ，搖桿CD長度的曲柄搖桿機構。

下面根據圖解結果，對θ取不同范圍時研究曲柄搖桿機構極位夾角θ與搖桿擺角ψ的關系。

1 Ⅰ型曲柄搖桿機構

Ⅰ型曲柄搖桿機構在兩極位時，機架A,D分布于極位點C1，C2兩側，所以在用圖解法時以C1C2為弦的圓周角∠C1AC2=θ應在遠離D的C1C2的一側找。即得到圖1，由圖可知E,F,A和D處于C1C2異側，可得：

圖2 Ⅰ型曲柄搖桿機構

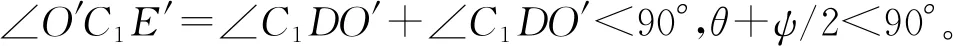
2 Ⅱ型曲柄搖桿機構

(1)θ=90°的情況。圖解法得圖3，由圖可知，θ=90°時，C1C2是圓的直徑，由圖分析參數間的關系特點：θ=90°時，對于ψ∈(0,∏),C∈(0,∞)任意取值，都可作出符合要求的Ⅱ型曲柄搖桿機構。

圖3 θ=90°的Ⅱ型曲柄搖桿機構

結論2: Ⅱ型曲柄搖桿機構θ=90°時,ψ∈(0,∏), ∈(0,∞)。

(2)θ>90°的情況。圖解法得圖4，由圖可知，θ>90°時，C1C2D分布在圓中心O同側，由圖分析參數間的關系特點：θ>90°時，圓弧C1E,C2F>0，C1,C2,E,F,D分布在圓中心O同側,即有角度關系∠OC1D<90°,θ-90°<ψ/2,在弧上任意點可作為機架另一鉸點有解。

結論3：Ⅱ型曲柄搖桿機構θ>90°時， 90°<θ<90°+ψ/2。

圖4 θ>90°的Ⅱ型曲柄搖桿機構

(3)θ<90°的情況。圖解法得圖5，由圖可知，θ<90°時，C1C2D分布在圓中心O兩側。參數間的關系特點：θ<90°時，θ,ψ,C之間互不影響，在θ∈(0,90°),ψ∈(0,∏),C∈(0,∞)任意取值，都可作出符合要求的Ⅱ型曲柄搖桿機構。

結論4：Ⅱ型曲柄搖桿機構θ<90°時，ψ∈(0,∏),C∈(0,∞)。

圖5 θ<90°的Ⅰ型曲柄搖桿機構

由結論2、3、4可知，Ⅱ型曲柄搖桿機構極位夾角的取值范圍為θ∈(0°,180°)。即Ⅰ型曲柄搖桿機構的極位夾角θ∈(0°,90°)，Ⅱ型曲柄搖桿機構的極位夾角θ∈(0°, ∏)。