跳躍機器人彈跳機構的設計

□ 秦 楠 □ 徐翰喬

大連科技學院 機械工程學院 遼寧大連 116052

1 設計背景

近年來,對機器人進行研究已經成為智能研究領域的熱點。輪式和履帶驅動的機器人只能在平坦地形上工作[1-2],步行和爬行機器人只具有一種直線爬行步態,應對較高障礙物或溝渠能力較弱[3-4]。跳躍機器人能夠跳躍越過障礙物和地面溝渠,可以彌補只能在平坦地形上工作的機器人的缺陷,滿足通過較高障礙物或溝渠地形的功能要求[5-6]。筆者對跳躍機器人彈跳機構進行設計。

2 設計方案

跳躍機器人彈跳機構采用間歇跳躍方式,通過機械和彈簧儲存能量。儲存的能量釋放時,能帶動整個機器人跳躍到空中,并通過缺齒齒輪作用完成周期性跳躍。

3 工作原理

跳躍機器人彈跳機構由彈簧儲能裝置和中間連桿裝置組成,由電機帶動缺齒齒輪、彈簧完成跳躍動作。當直齒輪與缺齒齒輪嚙合時,與直齒輪同軸的帶輪也產生轉動,連接在帶輪上的鋼絲繩越來越短,機構的上臺板會沿著兩根圓柱桿向下運動,從而使四根連桿位置發生變化,使彈簧產生拉伸變形儲備彈性勢能。當直齒輪脫離缺齒齒輪時,彈簧由拉伸狀態開始劇烈收縮,通過連桿傳遞作用力至上臺板,使上臺板向上做加速運動,釋放彈簧的彈性勢能,完成跳躍機器人的跳躍動作。整個跳躍機器人在缺齒齒輪的作用下實現連續間歇跳躍動作。所設計的跳躍機器人彈跳機構如圖1所示。

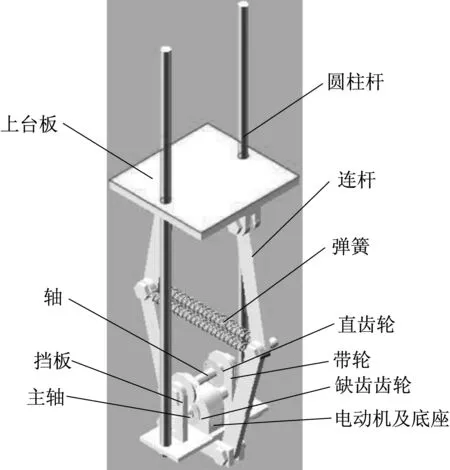
▲圖1 跳躍機器人彈跳機構

為了達到控制彈跳機構能量釋放的目的,采用缺齒齒輪結構。當兩個齒輪處于嚙合狀態時,彈跳機構處于蓄能狀態。當缺齒齒輪轉到缺齒的位置時,直齒輪與缺齒齒輪脫離嚙合狀態,不再嚙合。此時,控制彈簧處于拉伸變形狀態的力會消失,彈簧恢復到原來保持彈跳機構平衡的狀態,在這個過程中會給連桿一個向內運動的力,同時使上臺板沿著兩根圓柱桿向上運動,從而帶動整個彈跳機構向上運動,完成跳躍機器人的跳躍動作。

采用電動機兩端帶動兩個齒輪傳動的設計方案,如圖2所示。

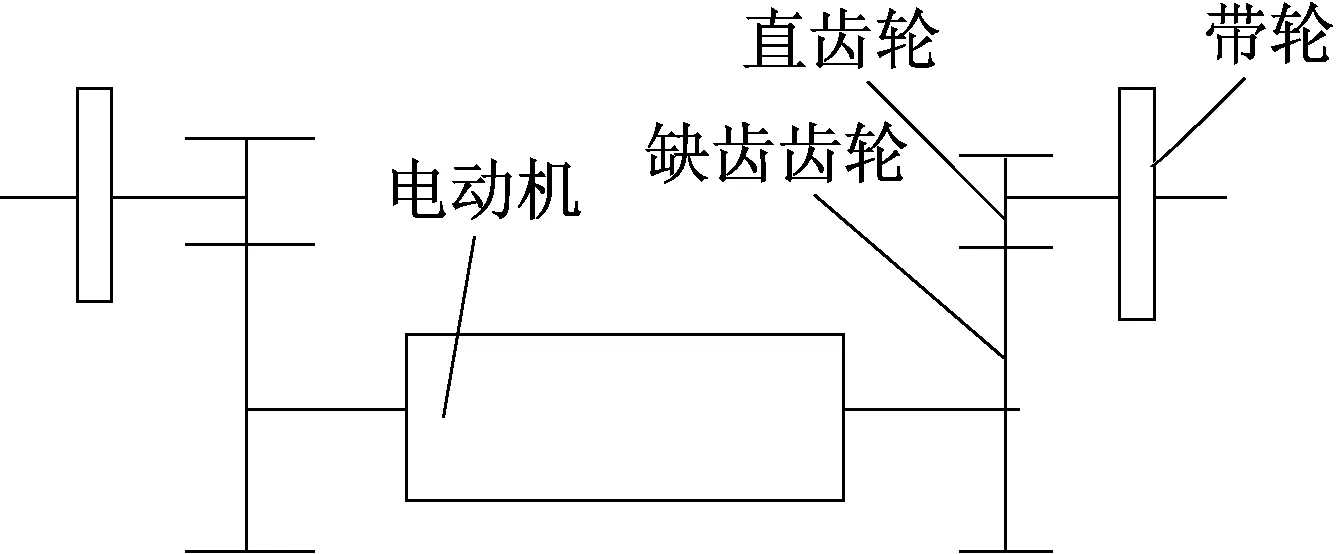
▲圖2 齒輪傳動設計方案

在電動機兩端伸出兩根軸,動力通過兩對缺齒齒輪與直齒輪傳遞到帶輪上。在帶輪上纏有鋼絲繩,與上臺板連接在一起。當電動機轉動時,兩對齒輪嚙合傳動,傳動軸帶動帶輪轉動,兩端鋼絲繩同時帶動上臺板下移。這一設計方案可以使鋼絲繩受力方向保持豎直,能夠更好地保持彈跳機構的平衡。

4 參數計算

基于跳躍機器人彈跳機構的結構和彈跳過程,對彈跳機構進行參數計算。建立跳躍機器人計算模型,如圖3所示。

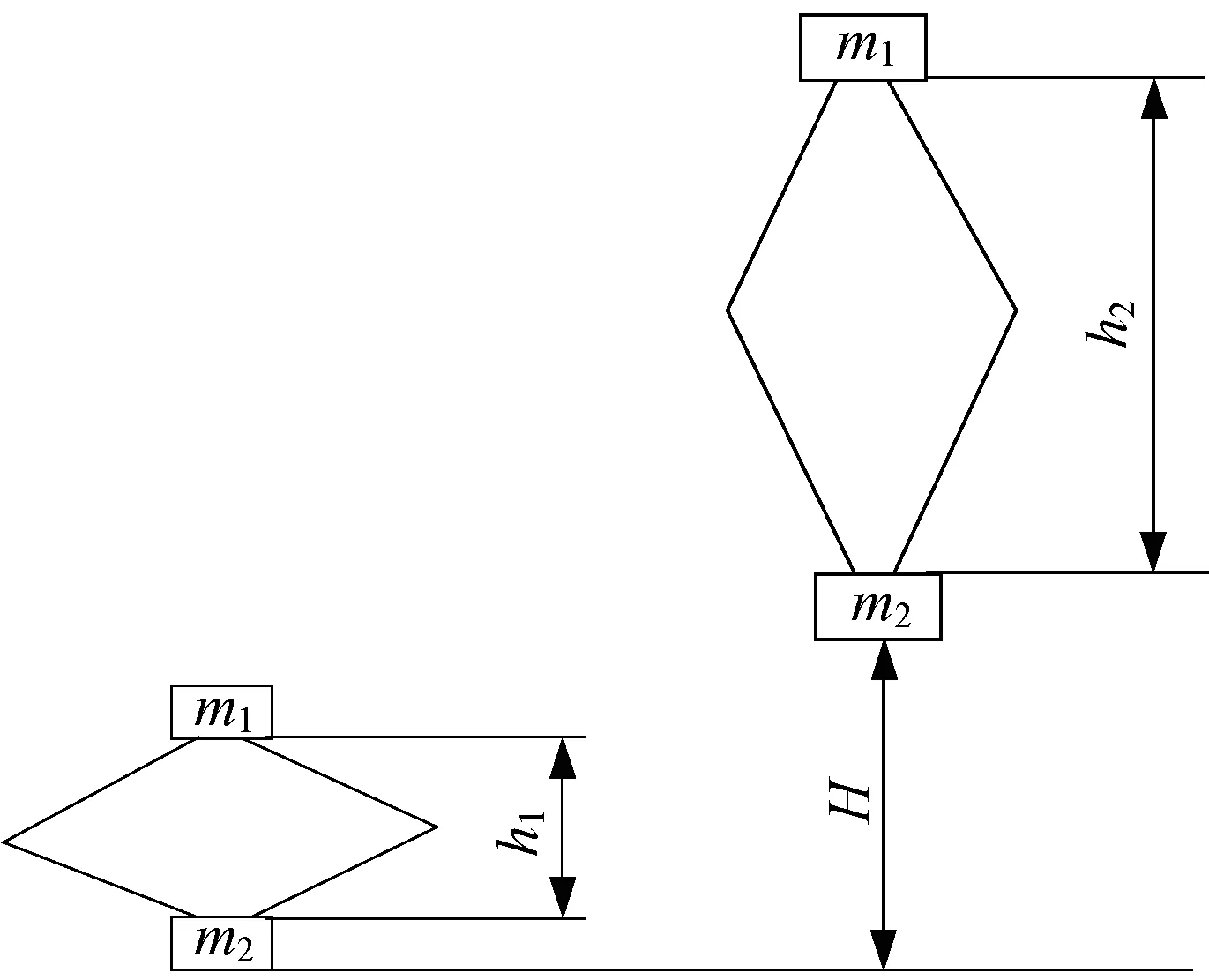
▲圖3 跳躍機器人計算模型

整個跳躍機構在起跳前和起跳后系統總能量保持不變,于是有:

m1gh1+k(Δx)2η/2=m1g(H+h2)+m2gH

(1)

式中:m1為上滑塊質量,m1=0.5 kg;m2為下滑塊質量,m2=1.65 kg;H為跳躍高度,H=1 000 mm;h1為彈簧儲能裝置釋放前四連桿機構的高度,h1=75 mm;h2為彈簧儲能裝置釋放后四連桿機構的高度,h2=190 mm;k為彈簧系數;Δx為彈簧理論伸長量,Δx=97 mm;η為彈簧效率,η=0.9。

代入數值對式(1)進行計算,可以得到彈簧系數為5.1 N/mm。由于彈跳機構中采用雙彈簧,由此實際彈簧系數為2.55 N/mm。

對彈簧進行線性計算,有:

Fmax=k(Δx+10)

(2)

式中:Fmax為彈簧最大載荷。

對式(2)進行計算可以得到彈簧所承受的最大載荷為272.85 N。通過對彈簧工作載荷進行分析,彈跳機構彈簧屬于Ⅲ類載荷彈簧,拉簧型式采用LⅢ型。筆者選用碳素彈簧鋼絲,材料的許用剪切應力[τ]為760 MPa。

彈簧鋼絲曲度因數K為:

(3)

式中:C為旋繞比。

彈簧鋼絲直徑d為:

(4)

初步選定C為8,根據式(3)計算得到曲度因數為1.18。由式(4)計算得到彈簧鋼絲直徑為2.95 mm,取標準值為3 mm。彈簧主要尺寸參數見表1。

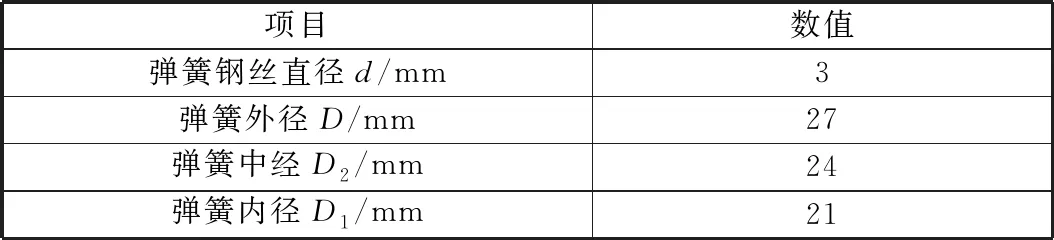
表1 彈簧主要尺寸參數

彈簧有效工作圈數N為:

(5)

式中:G為彈簧材料切變模量,G=79 000 MPa。

由式(5)計算得到彈簧有效工作圈數為20.57,取21。考慮兩端并緊一圈,則總圈數N1為23。

彈簧為拉伸彈簧,于是有:

F=Fmax/n

(6)

式中:F為彈簧極限載荷;n為安全因數,n=0.8。

由式(6)計算得到彈簧極限載荷為341.06 N。由于彈簧圈數由20.57調整為23,因此彈簧的伸長量與彈簧極限載荷也有相應調整。彈簧伸長量λ為:

(7)

由式(7)計算得到彈簧伸長量為135.57 mm。

彈簧節距p為:

p=d+λ/N1+δ

(8)

式中:δ為彈簧相鄰兩圈的間距。

在彈簧極限載荷作用下,彈簧相鄰兩圈的間距不小于彈簧鋼絲直徑的1/10,取2 mm,則由式(8)計算得到無載荷作用下節距為10.89 mn。

彈簧自由長度L0為:

L0=N1p+1.5d

(9)

由式(9)計算得到彈簧自由長度為254.97 mm,取255 mm。

彈簧螺旋升角γ為:

(10)

由式(10)計算得到無載荷作用下彈簧螺旋升角為8.22°,滿足螺旋升角在5°～9°范圍內的要求。

彈簧鋼絲展開長度L為:

L=πD2N1/cosγ

(11)

由式(11)計算得彈簧鋼絲展開長度為1 751.27 mm。

彈簧剛度Kp為:

(12)

由式(12)計算得到當彈簧總圈數為23時,彈簧剛度為1.77 N/mm。

穩定性b為:

b=L0/D2

(13)

彈簧采用兩端固定支座,由式(13)計算得到彈簧穩定性為10.625,大于5.3,因此需要對彈簧進行穩定性驗算:

Fc=CuKpL0>F

(14)

式中:Fc為穩定時的臨界載荷;Cu為不穩定因數,Cu=0.03。

對式(14)進行計算,得到彈簧穩定時的臨界載荷為13.54 N,小于彈簧極限載荷,因此在進行彈簧結構設計時,必須加裝導桿,導桿與彈簧的間隙建議為3～4 mm,用于保證彈簧使用時的穩定性。

5 結束語

跳躍機器人采用跳躍式運動方式前行,具有較強的自主運動能力[7-8]。筆者對跳躍機器人彈跳機構進行了設計,強化了跳躍機器人的地形適應能力,擴大了自主式運動機器人的應用范圍[9-10]。由于跳躍機器人涉及機電、控制、動力學、運動學等眾多領域,因此未來仍需進行大量工作,在各領域繼續深入研究。