多級混合式齒輪箱動態特性分析*

□ 譚 昕

江漢大學 機電與建筑工程學院 武漢 430056

1 分析背景

多級混合式齒輪箱是兆瓦級風力發電機中的關鍵部件之一,需要承受極大的扭矩,輸出極大的傳動比,并保持15 a以上的工作壽命。多級混合式齒輪箱的動態特性對工作壽命有重要影響。整個齒輪傳動鏈的傳動誤差是齒輪箱內部的一個重要激勵,當齒輪傳動鏈的剛度表現出非線性特性時,這種內部激勵難以控制[1]。如果齒輪傳動鏈動態傳動誤差的頻率與齒輪傳動鏈的某階模態頻率相同或相近,那么齒輪箱將會發生共振,對齒輪箱工作壽命會產生極大影響。可見,研究齒輪箱動態傳動誤差激勵頻率與齒輪箱振動模態之間的關系是一項重要工作。

目前,研究主要集中在靜強度、固有頻率、振動模態分析等方面[2],通常應用集中質量法進行計算[3]。

筆者通過理論計算,推導齒輪傳動鏈動態傳動誤差的計算方程。采用Pro/E軟件對某型多級混合式齒輪箱進行整機三維建模,并將建立的整機三維模型導入ANSYS軟件,建立有限元模型[4],通過仿真計算得到齒輪箱整機約束振動模態。將理論計算得到的動態傳動誤差激勵施加到齒輪箱有限元模型上,通過仿真預測整機發生共振的可能性。

2 齒輪箱三維建模

筆者以某型兆瓦級風力發電機多級混合式齒輪箱為例,其結構簡圖如圖1所示。基于相關參數在Pro/E軟件中進行三維參數化建模,以.x_t格式文件導入Romaxwind軟件,生成整體虛擬樣機,加載后通過虛擬仿真運行獲得齒輪傳動鏈相關剛度矩陣和位置矩陣。多級混合式齒輪箱三維模型如圖2所示。

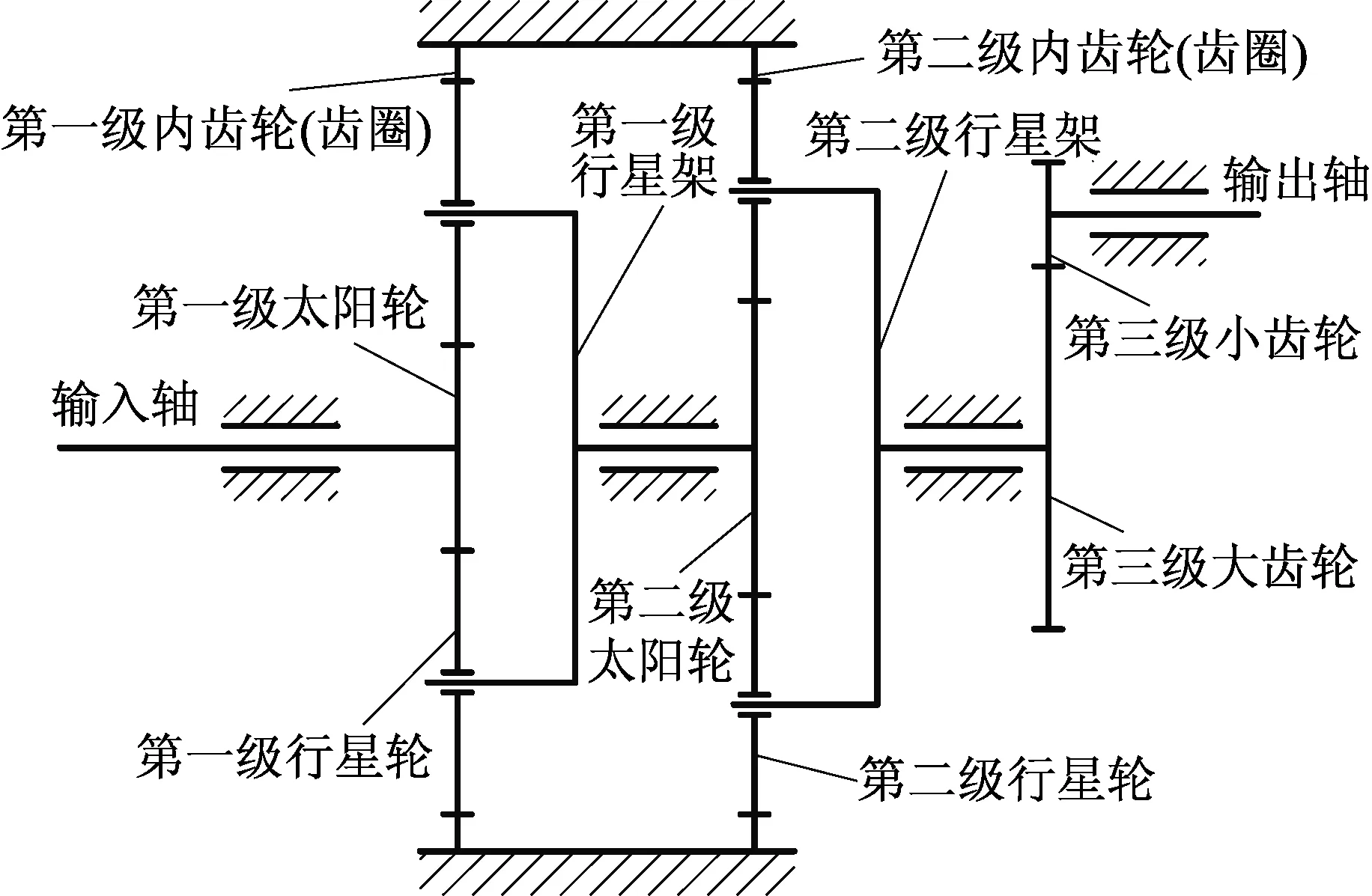
▲圖1 多級混合式齒輪箱結構簡圖

▲圖2 多級混合式齒輪箱三維模型

3 齒輪傳動鏈傳動誤差建模

傳動誤差分為靜態傳動誤差Ed和動態傳動誤差Es兩種,兩者之間的關系為[5]:

Ed=DT+Es

(1)

式中:DT為靜態傳動誤差Es與動態傳動誤差Ed之間的補償值。

DT為:

(2)

式中:[K]為齒輪傳動鏈的時變剛度矩陣;[F]為齒輪傳動鏈的位置矩陣;r為嚙合點處的曲率半徑;c為阻尼因數;i為總傳動比;ψ為正交轉置矩陣。

多級齒輪傳動鏈的總傳動誤差Δθ可以表示為[6]:

(3)

式中:im為第m級傳動的傳動比,m=2,3,…,N;Δθg為第g級傳動的傳動誤差,g=1,2,…,N。

Δθg為:

(4)

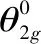
由齒輪傳動比誤差引起的傳遞誤差函數為:

(5)

式中:Δi12為傳動比誤差。

Romaxwind軟件中有一系列用于接收、處理傳動誤差的函數包,通過使用這些函數包,并應用式(1)～式(3),可以得到齒輪傳動鏈的動態傳動誤差曲線,如圖3所示。

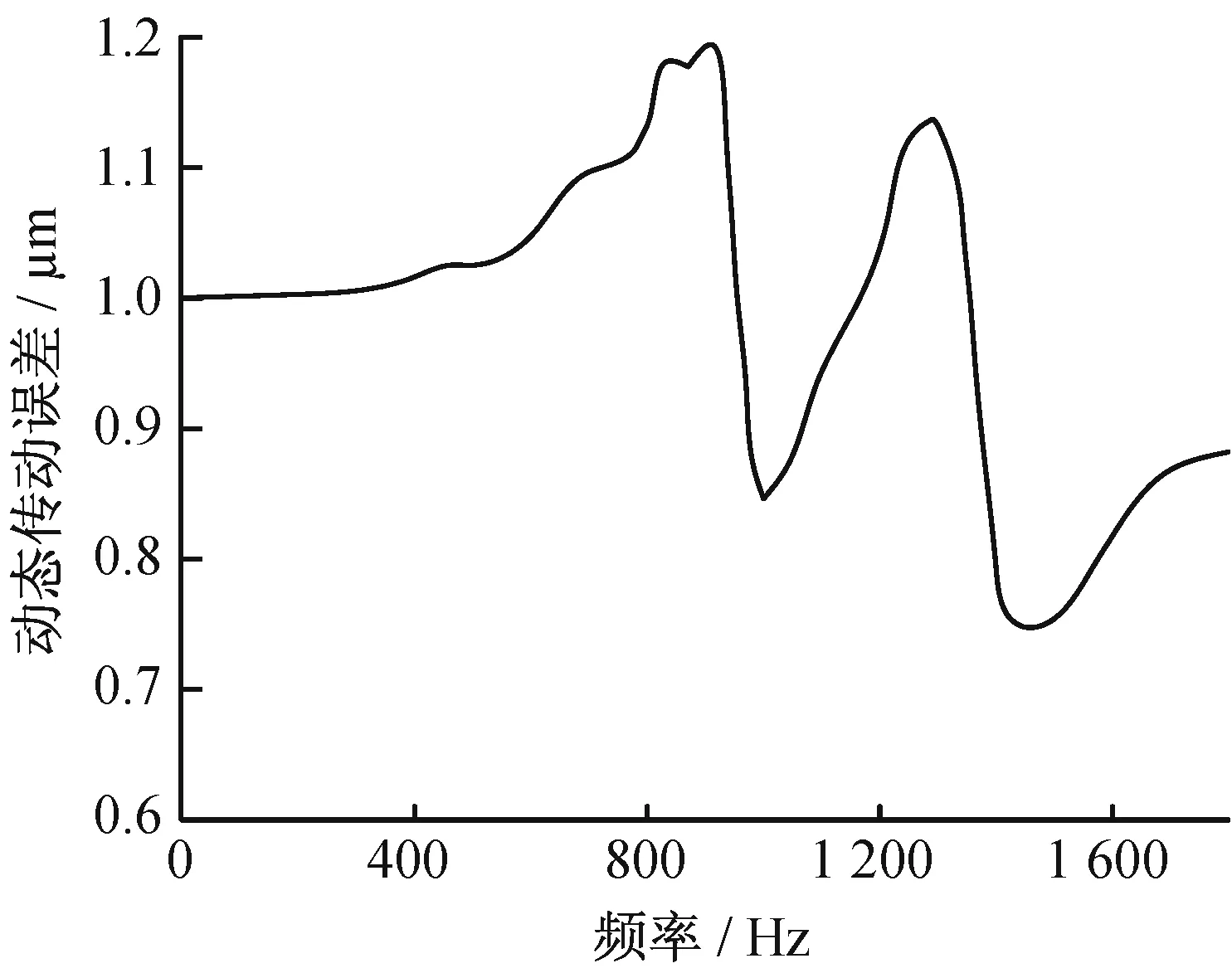
▲圖3 齒輪傳動鏈動態傳動誤差曲線

齒輪傳動鏈動態傳動誤差的峰值頻率見表1。齒輪傳動鏈的嚙合剛度表達式為[7]:

Fh=DhEd

(6)

式中:Dh為動態嚙合剛度;Fh為動態嚙合力。

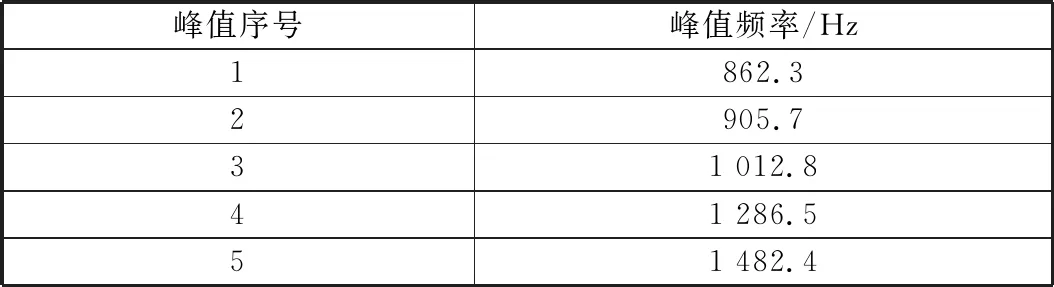
表1 齒輪傳動鏈動態傳動誤差峰值頻率

為了獲得準確的太陽輪與行星輪嚙合剛度變化規律,筆者采用有限元分析軟件進行處理。將太陽輪與行星輪系統單獨取出,設置行星輪系軸承系統全部為剛性,以濾除軸承變形導致的嚙合剛度變化。將行星輪設置為靜止,將單個行星輪上承受的扭矩施加在太陽輪上。通過總傳動誤差計算得到嚙合剛度,這一計算步驟在一個嚙合周期中將進行數次[8]。

上述方法同樣適用于行星輪與齒圈的嚙合過程。經過處理后,動態嚙合剛度曲線如圖4所示。

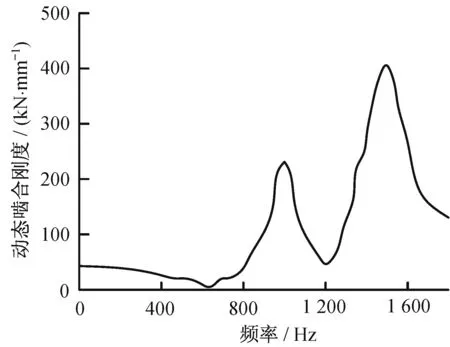
▲圖4 動態嚙合剛度曲線

整個齒輪傳動鏈有兩組固有頻率和模態:① 各組件都旋轉時所具有的顯式模態;② 只有行星輪旋轉,太陽輪、齒圈和行星架都不旋轉時的退化模態。描述齒輪傳動系統動態特性的關鍵是了解嚙合相位如何激發系統的諧波響應。通常嚙合相位起源于行星齒輪嚙合的同步性和動態嚙合力的周期,如果某個嚙合頻率激發出某個模態,那么太陽輪、齒圈、行星架也會在該諧波頻率下出現共振[9]。

4 齒輪箱振動模態

通常認為激勵頻率與系統某模態頻率的偏差小于10%或成倍數關系時會發生共振,因此了解系統振動模態是控制動態特性的重要前提。由于自由模態是在無載荷、無約束條件下獲得的,主要反映的是系統剛度特性,因此筆者直接研究多級混合式齒輪箱的約束模態。約束施加于多級混合式齒輪箱前后端蓋及輸入輸出端軸承上,邊界條件為約束前后端蓋及輸入輸出軸承處的全部自由度,采用這種約束設置與實際情況是一致的[10]。

使用蘭喬斯算法在ANSYS軟件中對多級混合式齒輪箱三維模型進行模態仿真。根據傳動誤差峰值頻率,多級混合式齒輪箱在600～2 300 Hz頻段內模態產生共振的可能性最大,因此筆者提取該頻段內前十階振動模態頻率進行分析,見表2。

表2 多級混合式齒輪箱前十階振動模態頻率

對比動態傳動誤差的五個峰值頻率可知,三階至六階約束振動模態頻率與激勵峰值頻率較接近。與傳動誤差峰值頻率接近的四個振動模態如圖5所示。

▲圖5 多級混合式齒輪箱振動模態

由圖5可知,三階振動模態是橫向扭轉振動模態,在該模態下,多級混合式齒輪箱體上所有點的振動方向是一致的,作用在箱體接合部的壓力對振動幅度有明顯影響。四階振動模態是橫向彎曲振動模態,可由系統中三個平行軸上的時變軸向力激發。五階振動模態是擺動振動模態,可由太陽輪的動態嚙合力激發,模態振幅比較大。六階振動模態是扭轉彎曲振動模態,由于輸出軸承受較大的時變彎矩和扭矩,因此通常會產生周期性軸向和徑向變形,從而可能激發這一振動模態。

由于多級混合式齒輪箱三階、四階、五階、六階振動模態頻率與傳動誤差峰值頻率很接近,隔離裕度小于10%,因此多級混合式齒輪箱在工作時存在共振風險。若發生共振,振動能量尖峰以905 Hz為主。觀察上述四種振動模態可知,多級混合式齒輪箱中段剛度不足是導致振動模態頻率偏低的主要原因。多級混合式齒輪箱中段剛度不足的原因包括:① 太陽輪與轉軸的連接剛度較低;② 內齒圈結構剛度過低;③ 軸承與軸承座在軸向的支承剛度不足。

為避免發生共振,有兩種優化方法:① 改變傳動誤差激勵頻率;② 調整結構以改變約束模態頻率。由于改變傳動誤差激勵頻率相對而言難度更大,因此筆者采用調整箱體結構,進而改變振動模態頻率的優化方案。具體措施為:① 縮短全部行星傳動中太陽輪主軸長度,對太陽輪與主軸的配合尺寸采用更高精度的公差等級,并采用花鍵連接太陽輪和主軸;② 適當加大內齒圈寬度和厚度;③ 調整角接觸球軸承游隙,以提高支承剛度。

5 試驗臺架測試

根據上述優化方案重新設計多級混合式齒輪箱,加工等比例實物模型,并搭建多級混合式齒輪箱動態特性試驗臺架[11],如圖6所示。這個測試臺架由一臺3 kW電機驅動,測試臺架上有四個信號采集單元,負載端為磁粉制動器。四個信號采集單元通過專用插槽固定在齒輪箱箱體上以獲得振動信號。

▲圖6 多級混合式齒輪箱動態特性試驗臺架

多級混合式齒輪箱箱體上布置四個信號采集點。第一個采集點設置在前齒輪箱蓋上,因為這一段箱體結構較復雜,振動模態較多,且承受的載荷較大。第二個采集點設置在后齒輪箱蓋上,因為后齒輪箱蓋支撐輸出軸,應檢測其連接剛度。第三個采集點設置在第一級齒輪的軸承附近,以方便測試來自于軸承的激勵力信號。第四個采集點設置于輸入軸上,以測試輸入扭矩的變化。第一個和第二個采集點布置位置如圖7所示。

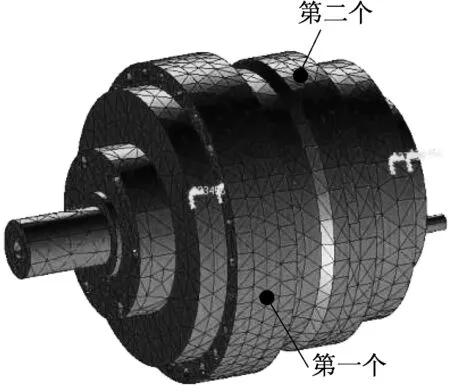
▲圖7 多級混合式齒輪箱信號采集點布置位置

由動態試驗獲得的多級混合式齒輪箱優化后振動模態頻率見表3,試驗測得多級混合式齒輪箱在600～2 300 Hz頻段內共有六個振動模態頻率。與表1比較可以發現,多級混合式齒輪箱結構優化后的振動模態頻率與動態傳動誤差峰值頻率相差較大,且在動態傳動誤差一階諧波作用下的頻率響應峰值與動態傳動誤差自身的頻率完全不同,發生共振的可能性明顯降低。

表3 優化后多級混合式齒輪箱振動模態頻率

另一方面,在動態傳動誤差高階諧波作用下的頻率響應峰值與動態傳動誤差自身的頻率也完全不同。由此可以得出結論,經過結構優化后的多級混合式齒輪箱在自身動態傳動誤差的激勵下發生共振的可能性很小。

6 結束語

筆者通過計算機軟件仿真分析與試驗相結合的方法,研究多級混合式齒輪箱動態特性,具有效率高、結果準確的特點。這一方法在Pro/E、ANSYS、Romaxwind三個通用軟件中進行,具有數據交換方便、結果精度高的優勢,對齒輪箱類機械系統動態特性的確定具有較好的適用性。

通過研究發現,對于齒輪箱類機械系統而言,在結構設計時應注意兩方面問題。

(1) 不能僅考慮系統輸入、輸出產生的振動激勵,齒輪箱內部傳動誤差引起的振動激勵也非常重要。在模態分析時,不僅要研究自由模態,而且應考慮約束模態對系統動態特性的影響。

(2) 應充分應用動態試驗來研究齒輪傳動系統的共振頻率,并以此作為結構設計改進的依據。尤其應考慮各結構件連接剛度對共振頻率的影響,盡可能使約束模態頻率避開共振激勵頻率。