改進風管送風方式對花椒冷藏庫流場的改善

郭晉楠 南曉紅 劉立軍

1 西安建筑科技大學建筑設備科學與工程學院

2 西安交通大學能源與動力工程學院

0 引言

庫內氣流組織特性對貨物貯藏品質影響顯著。庫內傳熱系數具有空間差異，造成貨物換熱不均勻[1]。因此研究者們對貨物擺放形式[2]以及貯藏環境參數控制和預測[3]等進行了研究。目前，在冷風機送風口加裝送風管道成為一種重要方法[4]。由于具有均勻、低速送風的特點[5]，纖維空氣分布系統（下文稱纖維風管）被逐漸應用于冷藏庫，但風管布置不合理容易造成庫內局部區域氣流組織較差的狀況，需調整送風方式以改善庫內流場。

本文采用數值模擬技術，分析設計工況下半圓式纖維風管氣流組織的不足，通過將風管變為四分之一圓式纖維風管，對庫內流場進行了優化研究。研究結果對纖維風管在冷藏庫中的應用以及提高花椒貯藏品質具有重要意義。

1 數值計算模型

1.1 幾何及物理模型

本研究的冷藏庫為某全自動化立體花椒冷藏庫，冷藏庫尺寸為90.6 m×35.1 m×23.0 m，體積約為68371 m3，總庫容量約為5000t，屬于高大空間。冷卻設備采用吊頂式冷風機。送風裝置為半圓附壁式纖維風管。庫內有七處貨物區，分別為貨物區A、B、C、D、E、F 和G。冷藏庫三維幾何模型見圖1（a）。在進行數值計算之前，對幾何及物理模型做合理假設：

（1）冷藏庫內貨物的物性參數恒定；

（2）空氣物性參數是常數，為不可壓縮流體；

（3）貨物區為均勻的多孔介質區，且熱物理性質在所研究溫度范圍內恒定；

（4）空氣和貨物之間的熱傳遞由熱傳導和熱對流機制控制，忽略輻射傳熱；

（5）計算模型的幾何和邊界條件都是對稱的，取該冷藏庫幾何模型的二分之一進行研究，如此，可節約計算資源和計算時間。簡化幾何模型如圖1（b）。

圖1 冷藏庫幾何模型及簡化示意圖

1.2 數學模型

1.2.1 控制方程

本研究針對空氣區和貨物區建立三維穩態流動換熱控制方程，包括：連續性方程，動量方程和能量方程以及k-ε 兩方程模型方程，其通用表達式[6]為：

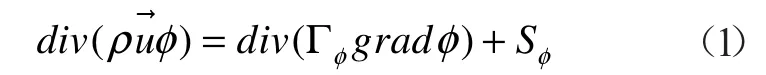
1.2.2 貨物區的處理

受冷風機送風作用，庫內空氣向貨物區滲流時受到花椒表面的阻力，這部分阻力在計算時作為流體動量方程的阻力源項，由Forchheimer 滲透定理確定，主要表現為黏性阻力和慣性阻力：

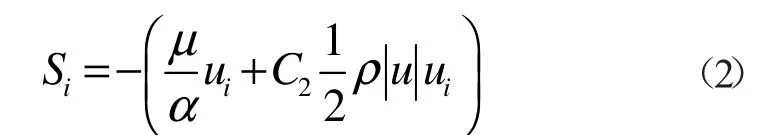
式中：μ為空氣動力黏度，Pa·s；α為貨物區（多孔介質區）滲透率，m2；C2為慣性阻力系數，1/m；ρ為空氣密度，kg/m3；ui為X、Y 和Z 方向分速度，m/s；|u|為空氣速度，m/s。

依據Ergun 方程[7]可得到粘性阻力系數和慣性阻力系數：

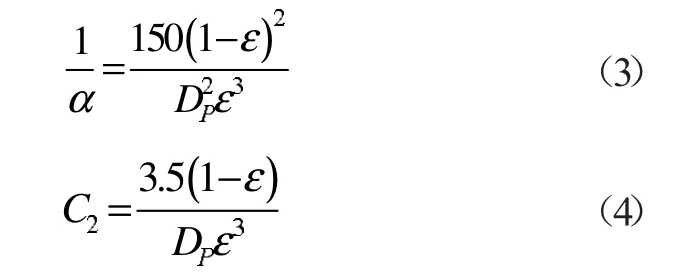
式中：ε 為貨物區的孔隙率；DP為貨物區裝袋的有效尺寸，m。

1.2.3 邊界條件

1）送風邊界

風管送風面：速度入口。風管總長度為80 m，斷面為半圓形，直徑約為2.1 m，管道側面九點鐘方向開設噴孔（孔徑約10 mm），如圖2 所示。依據廠家提供的設計參數，小孔噴射速度為0.30 m/s，未開孔管道面為大滲透送風，速度約為0.04 m/s。

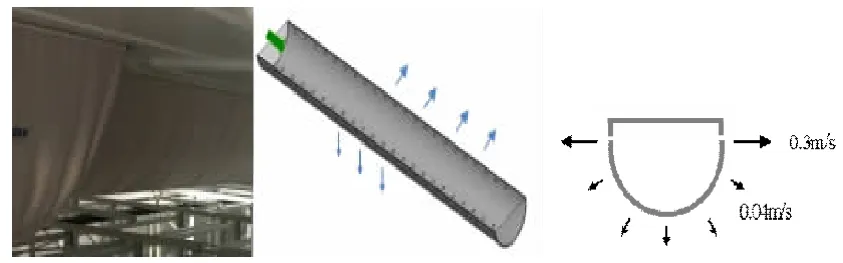
圖2 風管簡化幾何模型示意圖

庫內室內設計計算溫度為-5～-3 ℃，空氣流經冷風機后的溫差[8]為2～3 ℃，所以送風溫度定為-7 ℃。

2）出口邊界

冷風機回風口：自由出流，即該邊界的速度和溫度法向梯度為零。

3）墻體邊界

墻體速度邊界均為無滑移邊界，即速度為零。

四周外墻和屋頂與外界空氣進行對流換熱，故四周外墻和屋頂外墻熱邊界條件為第三類邊界條件，外表面與庫外空氣對流換熱系數[9]為23 W/(m2·K)，庫外空氣溫度為30.6 ℃。四周外墻墻體厚度150 mm，屋頂厚度200 mm，保溫材料均為聚氨酯。

地面與土壤接觸，熱流傳輸恒定，傳熱條件可定為定熱流量，故地面熱邊界條件為第二類邊界條件，熱流密度3 W/m2，墻體厚度200 mm，保溫材料為XPS（聚苯乙烯保溫板）。

4）冷風機邊界

風機外殼：無滑移邊界，即邊界速度為零。并假設其與室內無熱量傳遞，即壁面絕熱。

5）中心對稱面

中心面：對稱邊界，即所計算的物理量梯度為零。

2 網格無關性驗證及模型驗證

本文建立5 個不同網格數量的計算模型，網格劃分如圖3（a）。隨著網格數量增加，各區域溫度最大值均趨于穩定。從圖3（b）可以看出，當網格數量增加到265 萬時，各區域溫度最大值相對變化率為2.5%，故網格數量為265 萬時計算結果與網格數量無關。

圖3 網格劃分示意圖及網格數量對計算結果的影響

針對射流溫度衰減情況，當射流溫度與周圍空氣溫度不同時，趙榮義等人[10]提出出定量的研究結果計算公式（下文稱趙榮義計算式）如下：

此外，蔡增基等人[11]通過理論分析得出平面射流軸心溫度差衰減計算公式（下文稱蔡增基計算式）具體如下：

從圖4 中發現，模擬結果的射流軸心溫度與上述計算體系的衰減規律一致，最大相對誤差約49%，最小相對誤差1.7%，平均相對誤差2%，驗證了計算模型的可靠性。

圖4 射流軸心溫度衰減

當送風溫度為-7 ℃時，貨物區A～G 最高溫度為-5.8 ℃，不滿足花椒貯藏工藝要求（-5 ℃～-3 ℃），如圖3（b）。當送風溫度為-5 ℃時，貨物最高溫度和最低溫度均介于-4.6 ℃～-3.8 ℃，滿足要求，如圖5。因此以送風溫度為-5 ℃時的傳熱模型進行研究。

圖5 送風溫度為-5 ℃時貨物區A～G 的最高溫度和最低溫度

3 氣流組織評價指標

目前，常用的氣流組織評價指標主要有3 類：送風有效性參數，污染物排除有效性參數及余熱排出效率和熱舒適參數[12]。本文采用不均勻系數及余熱排出效率對庫內氣流組織進行評價。溫度不均勻系數kt定義如下[13]：

余熱排出效率η 可用下式定義[13]：

式中：tp、tn、t0分別為回風溫度，貨物區平均溫度和送風溫度。余熱排出效率越高，節能潛力越大。

4 計算結果分析及評價

4.1 改進前后計算結果分析

由于纖維風管沿Y 軸方向布置，冷空氣集中匯于回風口，容易造成距離冷風機較遠的區域氣流組織較差。為改善此狀況，以總送風量不變為前提，將半圓式纖維風管改為四分之一圓式風管（如圖6），并使送風方向均朝向墻體。改進后送風邊界條件為：小孔噴射速度為0.6 m/s，未開孔管道面滲透風速為0.08 m/s。

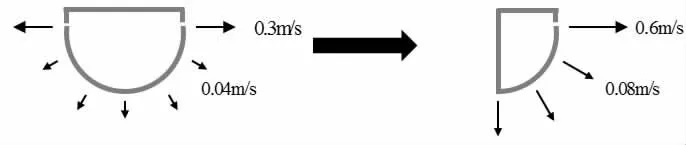
圖6 改進纖維風管送風模型示意圖

4.1.1 改進前后庫內速度場對比分析

從圖7 可以看出，在半圓式纖維風管送風模式下，y=45 m 截面的空氣最大速度為0.28 m/s，最小速度為0.04 m/s。在四分之一圓式纖維風管送風模式下，y=45 m 截面的空氣最大速度為0.36 m/s，最小速度為0.04 m/s。改進送風方式前后，貨物區周圍最大空氣速度相比改進之前增大29%，有利于庫內冷空氣和貨物進行換熱。

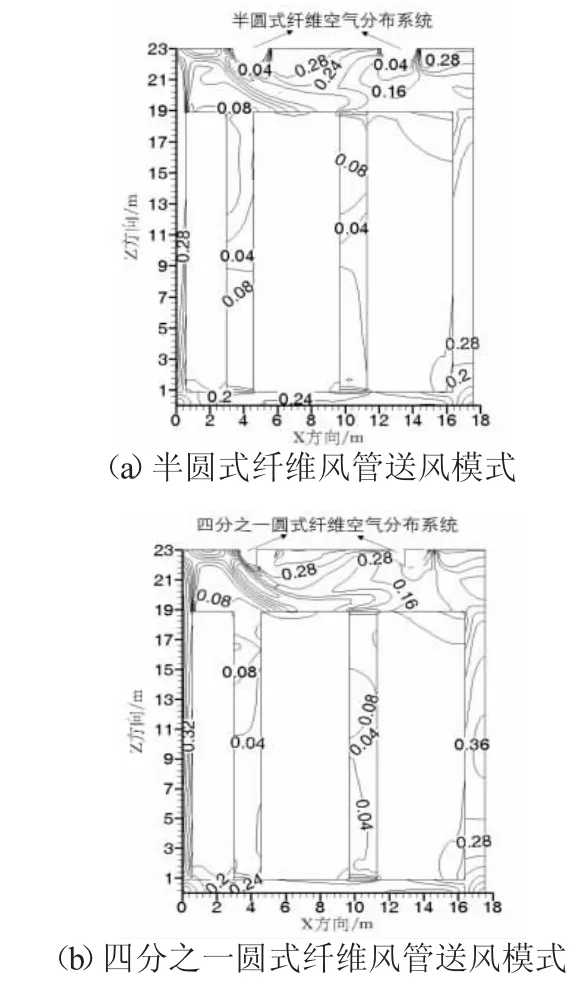
圖7 改進送風方式前后y=45 m截面速度分布圖（m/s）

4.1.2 改進前后庫內溫度場對比分析

從圖8 可以看出，在四分之一圓式纖維風管送風模式下，貨物區的溫度介于-4.45～-4.25 ℃，貨物區最大溫差為0.2 ℃，滿足花椒貯藏條件（-5～-3 ℃）。在半圓式纖維風管送風模式下，貨物區溫度介于-4.15～-4.45 ℃，貨物區最大溫差為0.3 ℃。改進后貨物區最大溫差降低33%，且改進前貨物溫度偏低。經過上述分析，使用四分之一圓式纖維風管送風模式有利于營造更加均勻的貯藏環境。

圖8 改進送風方式前后y=45 m 截面溫度分布圖（℃）

4.2 冷藏庫內氣流組織的評價分析

在貨物區以20 m 為步長沿Y 軸方向均勻建立五個截面，調取每個截面網格節點速度和溫度的值，按照式（7）和（8）進行氣流組織評價指標計算，結果如表1 所示。

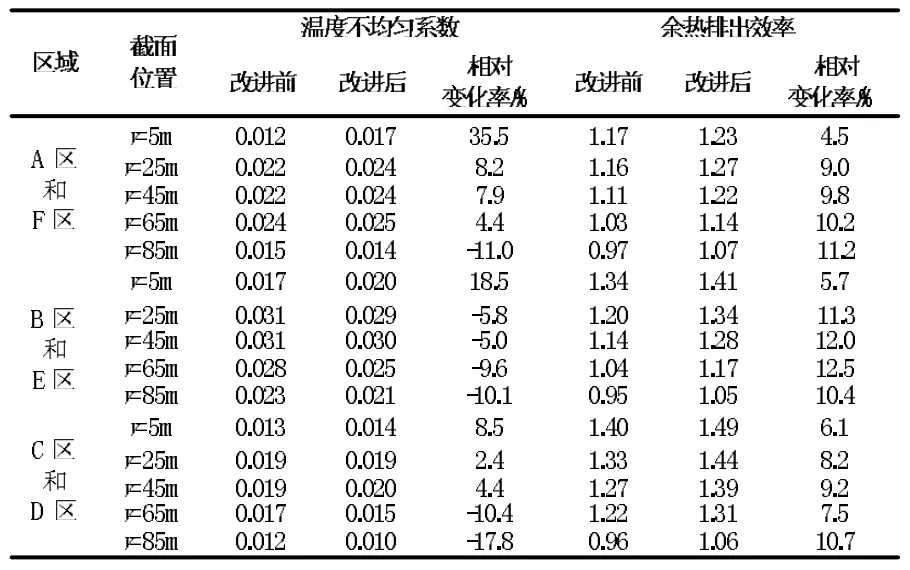
表1 氣流組織評價指標計算結果

從表1 可以看出，冷藏庫內貨物區溫度不均勻度有明顯差別：改進送風方式（即四分之一圓式纖維風管送風模式）后，y=65 m 和y=85 m 截面的貨物溫度不均勻系數比半圓式纖維風管送風模式下的溫度不均系數降低9.6%～17.8%，而y=5 m 和y=25 m 截面的貨物溫度不均勻系數均有所增大。由于距離冷風機較近的區域空氣流速大、換熱充分，貨物貯藏條件整體較好。而距離冷風機較遠的區域，空氣流速小，貨物貯藏條件整體較差，故改進送風方式后有效于改善距離冷風較遠區域的氣流組織特性。

對于庫內余熱排出效率，在半圓式纖維風管送風模式下，介于y=85 m 截面和y=90.6 m 墻體的區域余熱排出效率均低于0.95，該區域體積占冷藏庫總體積的6%。經改進送風方式，庫內所有貨物區的余熱排出效率均有所提高，最大增幅達12.5%，最小增幅為4.5%，最小余熱排出效率達1.05，較優化之前的0.95增大10.5%，有利于增強冷藏庫運行節能潛力。

5 結論

本文以韓城市某花椒冷藏庫為研究對象，建立庫內冷空氣流動與傳熱的三維數學求解模型，依據保持總送風量不變的原則，改進纖維風管送風方式，對比研究了改進送風方式前后庫內流場的分布情況，主要得出如下結論：

1）在四分之一圓式纖維風管送風模式下，貨物區最大溫差為0.2 ℃，相比改進前，貨物區最大溫差降低約33%，有利于營造更加均勻的貯藏環境。

2）改進送風模式后，距離冷風機較遠的區域的溫度不均勻系數較改進之前的貨物溫度不均系數降低9.6%～17.8%。使用四分之一圓式纖維風管進行送風，可以有效改善距離冷風機較遠區域溫度場的均勻性。

3）改進送風模式后，庫內貨物區所有區域不同位置的余熱排出效率較優化之前提高4.5%～12.5%。庫內最小余熱排出效率達1.05，較優化之前的0.95 增大10.5%。改進后的送風模式可以有效提高整個冷藏庫內的余熱排出效率，有利于冷藏庫運行節能。