高速鐵路跨度40 m雙線混凝土簡(jiǎn)支箱梁的約束扭轉(zhuǎn)效應(yīng)分析

趙富康， 藺鵬臻

(1.蘭州交通大學(xué)甘肅省道路橋梁與地下工程重點(diǎn)實(shí)驗(yàn)室， 蘭州 730070; 2.蘭州交通大學(xué)建筑與城市規(guī)劃學(xué)院， 蘭州 730070)

近年來(lái)，中國(guó)高速鐵路得到了充分的發(fā)展。箱梁由于具有出色的力學(xué)性能、構(gòu)造簡(jiǎn)單、耐久性好、施工便捷等優(yōu)點(diǎn)，成為高速鐵路橋梁的主要結(jié)構(gòu)型式[1-2]。但就雙線鐵路來(lái)說(shuō)，當(dāng)只有單線列車通過(guò)橋梁時(shí)，列車荷載相當(dāng)于在箱梁上施加一個(gè)不對(duì)稱的豎向荷載，使橋梁產(chǎn)生除縱向彎曲以外的約束扭轉(zhuǎn)與畸變[3-4]。此時(shí)箱梁的扭轉(zhuǎn)效應(yīng)增大，由約束扭轉(zhuǎn)變形引起的縱向正應(yīng)力占總縱向正應(yīng)力比例提高，翹曲位移加大[5-6]。因此研究雙線鐵路混凝土箱梁扭轉(zhuǎn)應(yīng)力對(duì)行車安全性具有重要的參考價(jià)值。劉保東等[7]對(duì)單箱單室波形鋼腹板連續(xù)梁和等效的普通混凝土箱型梁做了約束與畸變對(duì)比實(shí)驗(yàn)，得出混凝土頂?shù)装逄幍呐まD(zhuǎn)和畸變翹曲應(yīng)力所占比例不小。胡建華等[8]運(yùn)用烏氏第二定理推導(dǎo)了波形鋼腹板預(yù)應(yīng)力混凝土(PC)組合箱梁的剛性扭轉(zhuǎn)角計(jì)算公式。藺鵬臻等[9]分析了32 m跨徑雙線鐵路的畸變效應(yīng)，發(fā)現(xiàn)在單線活載偏心作用下，腹板和底板相交處翹曲比例系數(shù)最大，可達(dá)13.9%。蔣詩(shī)瑩等[10]以彈性開(kāi)口薄壁桿件約束扭轉(zhuǎn)為基礎(chǔ)，得到了鋼異形柱的截面幾何參數(shù)。張?jiān)５萚11]以約束扭轉(zhuǎn)微分方程為基礎(chǔ)，分析了帶懸臂板箱梁橫截面的各項(xiàng)剪應(yīng)力及合成扭矩。葉陽(yáng)升等[2]及劉勇等[12]指出為適應(yīng)中國(guó)西部山區(qū)和東部沿海等地區(qū)的高速鐵路快速發(fā)展，提高高速鐵路簡(jiǎn)支箱梁橋的經(jīng)濟(jì)性能，中國(guó)已開(kāi)始大力發(fā)展跨度40 m的整孔預(yù)制架設(shè)簡(jiǎn)支梁。湛敏[13]基于車橋耦合振動(dòng)分析方法，對(duì)比了高速鐵路跨徑40 m和32 m簡(jiǎn)支箱梁的動(dòng)力性能，與32 m跨度相比，40 m跨度簡(jiǎn)支梁的自振頻率偏低，而梁體橫向加速度和梁體位移均偏大。

以上學(xué)者基本從波形鋼腹板組合橋或32 m普通混凝土箱梁出發(fā)，研究了箱梁約束扭轉(zhuǎn)的影響效應(yīng)，但40 m預(yù)制簡(jiǎn)支梁作為新型高速鐵路體系，由于薄壁結(jié)構(gòu)效應(yīng)，在單線運(yùn)行時(shí)出現(xiàn)的約束扭轉(zhuǎn)和畸變將對(duì)橋梁的受力安全性產(chǎn)生影響，此類問(wèn)題尚未見(jiàn)文獻(xiàn)研究。

因此在以上學(xué)者的基礎(chǔ)上，進(jìn)一步結(jié)合在建時(shí)速350 km/h高速鐵路為例，針對(duì)40 m整孔預(yù)制架設(shè)箱梁的約束扭轉(zhuǎn)效應(yīng)，采用理論法計(jì)算在設(shè)計(jì)活載作用下的約束扭轉(zhuǎn)應(yīng)力分布規(guī)律及截面特性，并與精細(xì)有限元仿真分析結(jié)果進(jìn)行驗(yàn)證，綜合分析40 m簡(jiǎn)支箱梁的約束扭轉(zhuǎn)效應(yīng)及其參數(shù)變化對(duì)翹曲應(yīng)力的影響。

1 箱梁約束扭轉(zhuǎn)的基本方程

1.1 約束扭轉(zhuǎn)荷載

對(duì)于雙線高速鐵路橋梁，當(dāng)雙線列車完全同步行進(jìn)時(shí)，符合對(duì)稱受力方式，但實(shí)際上這種情況十分少見(jiàn)，在運(yùn)營(yíng)期絕大多數(shù)時(shí)間段內(nèi)雙線鐵路都會(huì)存在偏心荷載作用，其示意圖如圖1所示，雙線高速鐵路橋梁在僅有單線列車運(yùn)行時(shí)，對(duì)箱梁而言，相當(dāng)于作用一個(gè)偏心荷載，此時(shí)就會(huì)使橋梁產(chǎn)生除縱向彎曲以外的約束扭轉(zhuǎn)與畸變效應(yīng)。

圖1 偏心荷載示意圖Fig.1 Schematic diagram of eccentric load

如圖2所示，根據(jù)截面荷載等效原則[14]，可將作用于截面的偏心荷載分解為3種獨(dú)立的變形模型：豎向彎曲荷載，如圖2(d)所示；剛性扭轉(zhuǎn)荷載，如圖2(e)所示；畸變荷載，如圖2(f)所示。

ΣP為軌道受到的總壓力；Pe為偏心荷載引起的偏心扭矩值圖2 偏心荷載的分解Fig.2 Decomposition of eccentric load

荷載分解方式，依據(jù)扭轉(zhuǎn)荷載分解原理[14]，可確定作用在斜腹板箱梁上的特種活載集中力引起的剛性扭轉(zhuǎn)荷載。

(1)

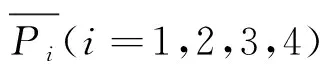
1.2 約束扭轉(zhuǎn)翹曲位移

箱梁在偏心荷載作用下會(huì)發(fā)生兩種扭轉(zhuǎn)，一種是箱梁扭轉(zhuǎn)時(shí)其縱向纖維伸縮沒(méi)有受到約束的自由扭轉(zhuǎn)，此時(shí)只產(chǎn)生扭轉(zhuǎn)剪應(yīng)力τk；另一種是由于邊界條件的因素導(dǎo)致箱梁縱向纖維之間的變形受到約束的約束扭轉(zhuǎn)，此時(shí)除產(chǎn)生自由扭轉(zhuǎn)剪應(yīng)力τk以外，還將在截面上產(chǎn)生翹曲正應(yīng)力σw及約束扭轉(zhuǎn)剪應(yīng)力τw。

已知自由扭轉(zhuǎn)下的縱向位移公式為[14]

(2)

由于θ′(z)是剛性扭轉(zhuǎn)時(shí)截面縱向變形沒(méi)有受到約束時(shí)的一個(gè)常數(shù)項(xiàng)，與z軸無(wú)關(guān)，無(wú)法反映結(jié)構(gòu)真實(shí)的翹曲情況。因此將自由扭轉(zhuǎn)縱向位移公式中的扭率θ′(z)用翹曲率β′(z)來(lái)替換，使之成為烏曼斯基假定下的約束扭轉(zhuǎn)位移模型[14]：

(3)

式(3)中：u(z,s)為截面各點(diǎn)的縱向位移；β′(z)為截面翹曲率，不等于θ′(z)，是關(guān)于z的一個(gè)待求函數(shù)。

1.3 約束扭轉(zhuǎn)正應(yīng)力

根據(jù)力的平衡條件可知截面上的翹曲產(chǎn)生的軸向內(nèi)力及彎矩是自相平衡的，因此對(duì)約束扭轉(zhuǎn)下的縱向位移求導(dǎo)，得到約束扭轉(zhuǎn)截面各點(diǎn)的軸向應(yīng)變和翹曲應(yīng)力，然后將其代入自相平衡的方程中，根據(jù)薄壁桿件結(jié)構(gòu)力學(xué)理論可得到薄壁箱梁的約束扭轉(zhuǎn)正應(yīng)力[14]，其形式與初等梁彎曲應(yīng)力表達(dá)式形式上一致。

(4)

1.4 約束扭轉(zhuǎn)剪應(yīng)力

在整個(gè)梁體上面任意取一箱壁單元ds×dz進(jìn)行應(yīng)力狀態(tài)分析，根據(jù)彈性力學(xué)微元平衡方法建立該點(diǎn)的平衡方程，最后再根據(jù)翹曲應(yīng)力和自由扭轉(zhuǎn)應(yīng)力產(chǎn)生的扭矩和外扭矩平衡關(guān)系可以得到約束扭轉(zhuǎn)剪應(yīng)力[14]。

(5)

式(5)包含兩項(xiàng)，第一項(xiàng)為自由扭轉(zhuǎn)剪應(yīng)力，第二項(xiàng)是約束扭轉(zhuǎn)剪應(yīng)力，其形式與初等梁理論下的剪應(yīng)力表達(dá)式一致。

1.5 約束扭轉(zhuǎn)微分方程

首先箱梁截面的抵抗扭矩是自由扭矩和約束扭矩之和，即：

(6)

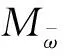
箱梁截面扭轉(zhuǎn)角與廣義翹曲位移有如式(7)所示的微分關(guān)系式：

(7)

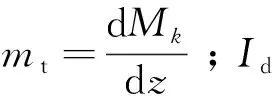
(8)

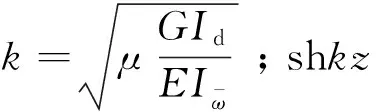
為確定積分常數(shù)，可對(duì)β(z)、θ(z)求各階導(dǎo)數(shù)，再根據(jù)箱梁邊界條件來(lái)求解確定。其邊界條件如表1所示。

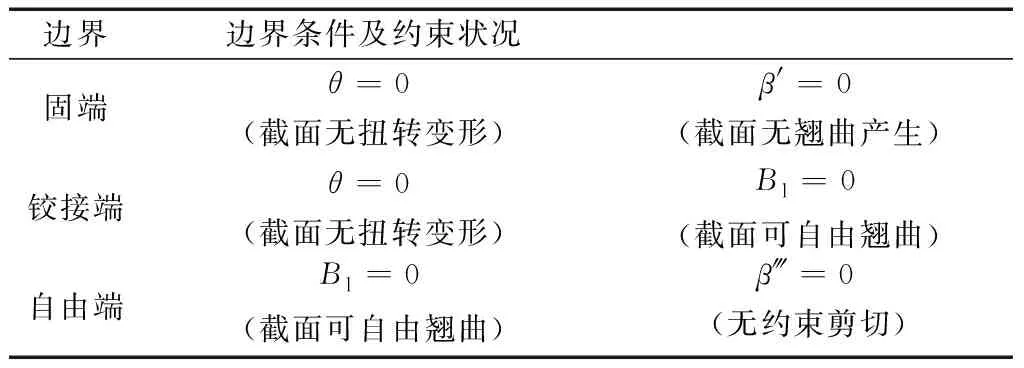
表1 箱梁的邊界條件Table 1 Boundary conditions of box girders

2 箱梁約束扭轉(zhuǎn)分析

2.1 箱梁的基本參數(shù)

圖3 箱梁截面圖Fig.3 Box girder section

2.2 約束扭轉(zhuǎn)基本效應(yīng)求解

2.2.1 荷載計(jì)算

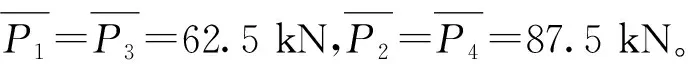
如圖1所示，設(shè)在距簡(jiǎn)支梁左側(cè)a、b、c、d處，分別存在一個(gè)集中扭矩：Ti=Pe=250×2.38=595 kN·m，(i=a、b、c、d)。

根據(jù)簡(jiǎn)支梁邊界約束條件θz=0，β″=0，當(dāng)z=0時(shí)，θ0=0，Bω0=0，因此可以推導(dǎo)得到扭轉(zhuǎn)角和翹曲雙力矩的表達(dá)式：

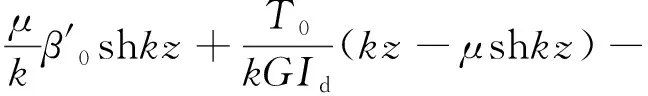
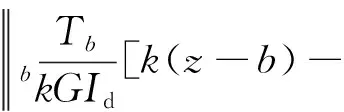
(9)

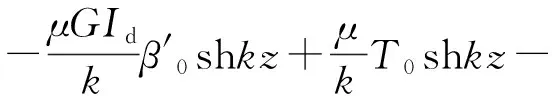
(10)

在z=l處，由邊界條件θz(l)=0、Bω(l)=0的關(guān)系，并聯(lián)立式(8)可推導(dǎo)梁端翹曲率和約束扭轉(zhuǎn)扭矩通式為

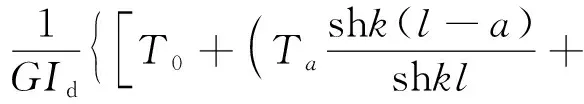
(11)

(12)

(13)

針對(duì)具體的橋梁來(lái)說(shuō)，首先根據(jù)邊界條件確定式(8)中積分常數(shù)，然后通過(guò)式(9)～式(13)確定扭轉(zhuǎn)角、翹曲雙力矩和約束扭矩，從而通過(guò)式(4)和式(5)可以得到實(shí)際橋梁在列車荷載作用下的約束扭轉(zhuǎn)效應(yīng)。

2.2.2 理論計(jì)算結(jié)果

按圖1所示的荷載對(duì)稱作用在簡(jiǎn)支梁跨中截面處，由式(9)計(jì)算沿梁長(zhǎng)方向各截面的扭轉(zhuǎn)角，如圖4所示。

圖4 扭轉(zhuǎn)角變化圖Fig.4 The change diagram of torsion angle

從圖4可以得到簡(jiǎn)支箱梁在發(fā)生扭轉(zhuǎn)時(shí)，其變化趨勢(shì)是從兩側(cè)桿端到跨中逐漸增大的過(guò)程，且在跨中截面達(dá)到最大值，變化趨勢(shì)成線性分布且沿跨中對(duì)稱。

取圖1其中單個(gè)集中力為研究對(duì)象，分別繪出集中扭矩作用在簡(jiǎn)支梁上l/4、3/4跨以及跨中截面處的翹曲雙力矩和約束扭矩沿梁軸方向變化曲線圖，如圖5所示。

圖5 翹曲雙力矩和約束扭矩變化圖Fig.5 The change diagram of warping double moment and constrained torque

由圖5可知，當(dāng)簡(jiǎn)化后的偏心集中力引起的集中扭矩分別加載在1/4跨、跨中和3/4跨截面時(shí)，跨中截面處的翹曲雙力矩最大，但是衰減很快，且沿集中扭矩位置向兩側(cè)越遠(yuǎn)，翹曲雙力矩越小，在箱梁兩端時(shí)，幾乎為0；約束扭矩在集中扭矩作用點(diǎn)處發(fā)生突變，且在跨中處約束扭矩達(dá)到最大值，1/4跨和3/4跨處的約束扭矩最大值占跨中處的83.35%。

2.3 約束扭轉(zhuǎn)效應(yīng)對(duì)比

通過(guò)對(duì)既有某時(shí)速350 km/h的高速鐵路雙線簡(jiǎn)支箱梁采用ANSYS中shell181建模，計(jì)算僅在單線偏心荷載最不利(按特種活載對(duì)稱布置在跨中截面位置)作用時(shí)，由于約束扭轉(zhuǎn)產(chǎn)生的翹曲正應(yīng)力和剪應(yīng)力。有限元模型如圖6所示。

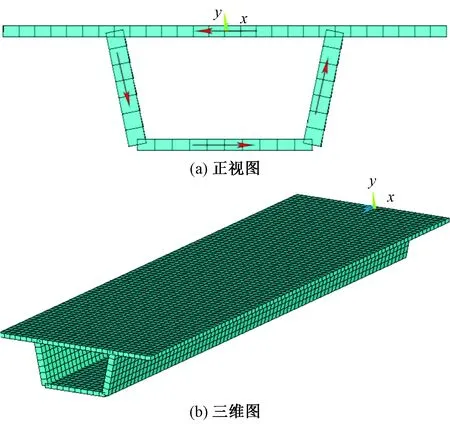
圖6 有限元模型圖Fig.6 Finite element model

通過(guò)結(jié)合式(4)和式(5)計(jì)算得到相應(yīng)的翹曲正應(yīng)力和剪應(yīng)力，與板殼單元有限元解進(jìn)行對(duì)比，結(jié)果如圖7所示。

一般由于在荷載作用點(diǎn)和邊界約束處，存在應(yīng)力集中現(xiàn)象，所以取距跨中截面0.5 m處，以減少跨中荷載作用處應(yīng)力集中的影響。

軸線左側(cè)是翹曲正應(yīng)力，右側(cè)是剪應(yīng)力圖7 跨中截面應(yīng)力分布Fig.7 Stress distribution on mid-span section

如圖7所示，由式(4)和式(5)計(jì)算得到的理論解與有限元解在沿截面橫向方向變化趨向一致，翹曲正應(yīng)力成反對(duì)稱分布，約束扭轉(zhuǎn)剪應(yīng)力成正對(duì)稱分布。觀察發(fā)現(xiàn)，有限元解普遍比初參數(shù)解略小，是因?yàn)槌鯀?shù)法中的公式大多基于烏曼斯基閉口薄壁直桿約束扭轉(zhuǎn)理論的3個(gè)基本假設(shè)條件下簡(jiǎn)化推導(dǎo)所得，而有限元法可以模仿真實(shí)箱梁的空間受力，所以初參數(shù)解結(jié)果比實(shí)際值偏大，因此有限元解可以更好地反映薄壁箱梁約束扭轉(zhuǎn)效應(yīng)。其中翹曲正應(yīng)力最大差值發(fā)生在圖3所示③號(hào)點(diǎn)，最大相對(duì)誤差達(dá)到66.6%；翼緣處的翹曲正應(yīng)力數(shù)值明顯大于截面其他部位，表明對(duì)40 m高速雙線鐵路箱梁來(lái)說(shuō)，翼緣板端部是約束扭轉(zhuǎn)效應(yīng)最突出的部位，設(shè)計(jì)時(shí)應(yīng)特別注意。

如圖8所示，沿箱梁縱向方向，隨著梁長(zhǎng)的增加，翼緣板端點(diǎn)(①號(hào)點(diǎn))、頂板與腹板交點(diǎn)(②號(hào)點(diǎn))和底板與腹板交點(diǎn)(③號(hào)點(diǎn))出現(xiàn)正對(duì)稱分布，且在跨中同時(shí)達(dá)到最大值。

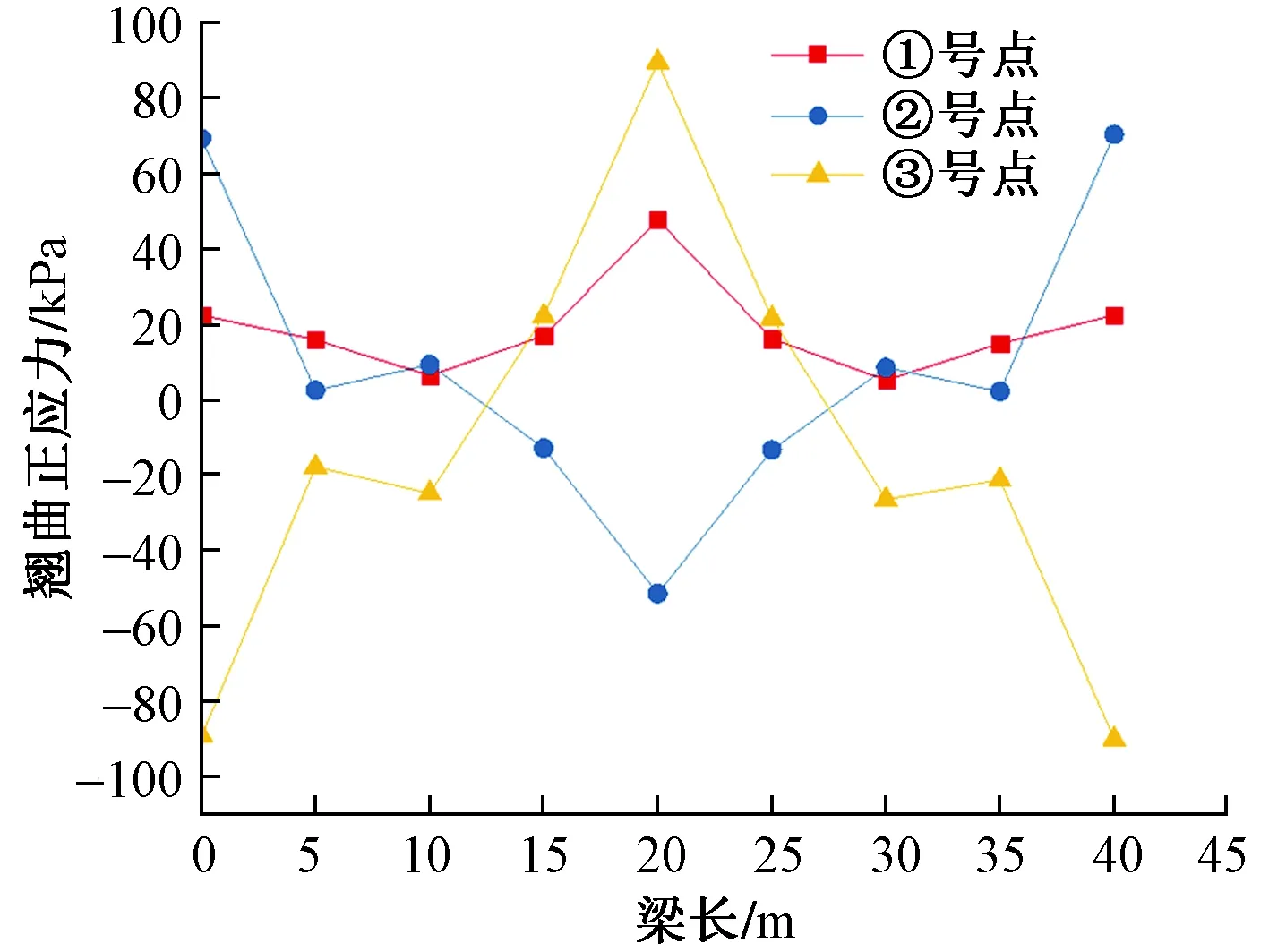
圖8 翹曲正應(yīng)力隨梁長(zhǎng)變化Fig.8 Warping normal stress changes with beam length

2.4 跨中約束扭轉(zhuǎn)應(yīng)力分析

為直觀地觀察約束扭轉(zhuǎn)下翹曲應(yīng)力在總應(yīng)力中所占的比重，確定約束扭轉(zhuǎn)效應(yīng)的大小，可以引入翹曲比例系數(shù)[9]λ，其表達(dá)式為

(14)

式(14)中：σω為約束扭轉(zhuǎn)翹曲正應(yīng)力；σ為單線荷載作用下縱向總應(yīng)力。

為反應(yīng)箱梁截面各控制點(diǎn)的約束扭轉(zhuǎn)程度，可以取箱梁左側(cè)分析。以箱梁頂、底板和懸臂端點(diǎn)為原點(diǎn)，橫截面長(zhǎng)度為橫坐標(biāo)；腹板則以頂板與腹板交點(diǎn)為原點(diǎn)，腹板長(zhǎng)為橫坐標(biāo)，分析翹曲比例系數(shù)λ的分布規(guī)律，如圖9所示。

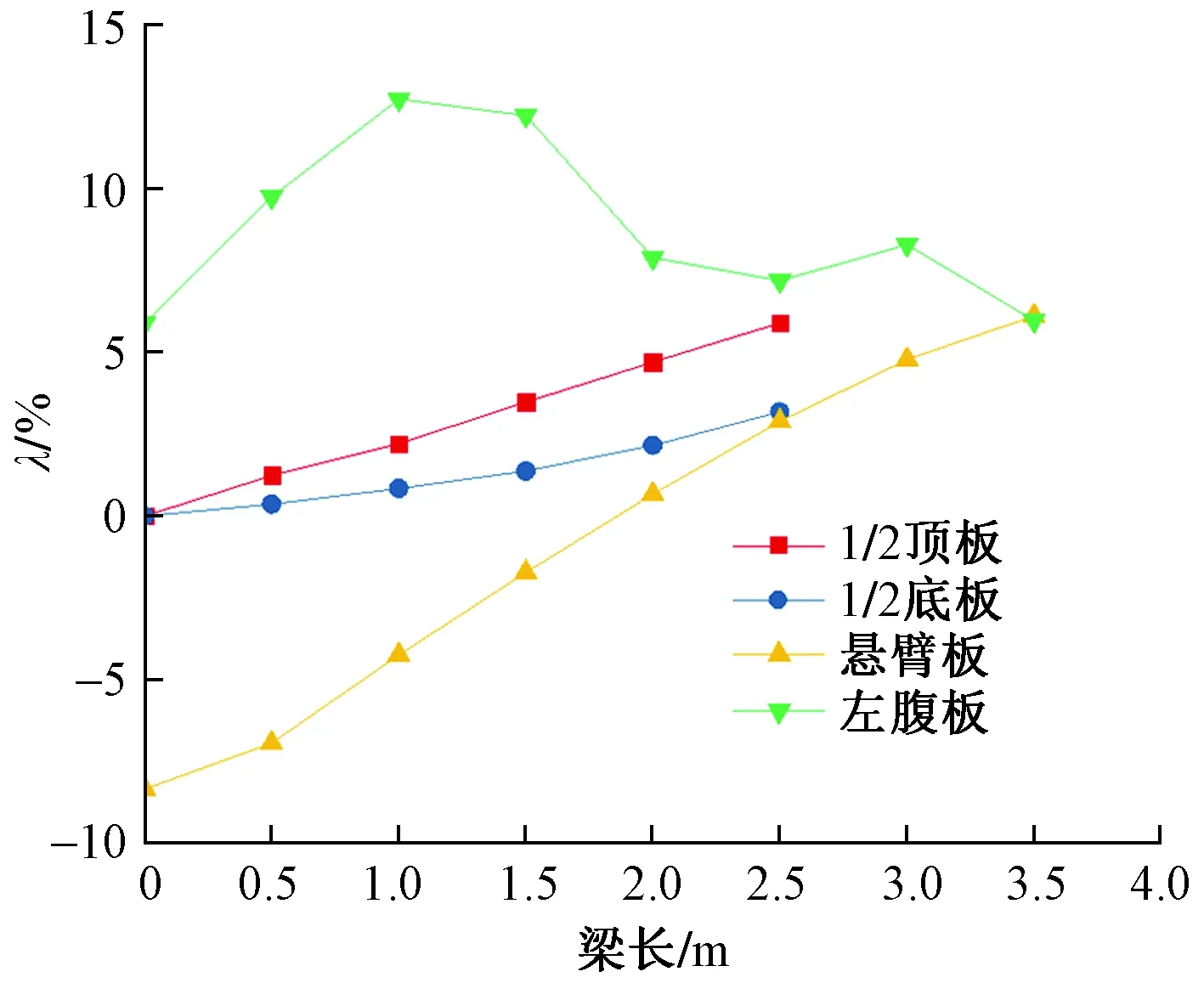
圖9 跨中截面翹曲比例系數(shù)Fig.9 Distortion ratio on mid-span section

由圖9可知，越遠(yuǎn)離截面中心，頂、底板的翹曲比例系數(shù)就越大，并呈線性增長(zhǎng)趨勢(shì)，其最大值均發(fā)生在與腹板交點(diǎn)處，且頂板的翹曲比例系數(shù)要比底板的大；懸臂板則呈現(xiàn)先減小后增大的趨勢(shì)，且數(shù)值有正有負(fù)，說(shuō)明懸臂板既承受壓應(yīng)力又承受拉應(yīng)力；腹板的翹曲比例系數(shù)要明顯大于頂、底板的翹曲比例系數(shù)，這是因?yàn)楦拱逯饕惺芗魬?yīng)力，故式(14)中的σ較小，導(dǎo)致數(shù)值整體偏大。

數(shù)值表明，翹曲比例系數(shù)λ在②號(hào)點(diǎn)處達(dá)到6.12%；在③號(hào)點(diǎn)處達(dá)到3.23%；在①號(hào)點(diǎn)達(dá)到9.16%。

3 結(jié)構(gòu)參數(shù)對(duì)約束扭轉(zhuǎn)效應(yīng)的影響分析

3.1 高寬比的影響

由圖3箱梁截面可知，在頂板、懸臂板和底板尺寸不變的情況下，把箱梁的高度以0.5 m步長(zhǎng)從1 m增加至8 m，也即箱梁的高寬比(h/b)以0.1的步長(zhǎng)從0.2增加至1.6，取如圖3所示箱梁的3個(gè)控制節(jié)點(diǎn)，按式(14)，結(jié)合ANSYS分析，計(jì)算跨中截面3個(gè)控制節(jié)點(diǎn)的翹曲比例系數(shù)變化圖，如圖10所示。

圖10 高寬比對(duì)翹曲比例系數(shù)的影響Fig.10 Effect of aspect ratio on distortion ratio

從圖10可看出3個(gè)控制節(jié)點(diǎn)處的翹曲比例系數(shù)都隨著h/b的增大而減小，當(dāng)h/b≥1.0時(shí)，3點(diǎn)處的翹曲比例系數(shù)都趨于穩(wěn)定，且3個(gè)值都很接近。因?yàn)榱焊咴酱螅魃刃詰T性矩Iω就越大，導(dǎo)致翹曲正應(yīng)力σω越小；在高寬比0.2～1.0時(shí)，③號(hào)節(jié)點(diǎn)處的翹曲比例系數(shù)減小的幅度最大，這與圖7中所得到翹曲應(yīng)力結(jié)果關(guān)系一致。

3.2 懸臂板寬度的影響

為考慮懸臂板寬度對(duì)翹曲比例系數(shù)的影響，以圖3所示箱梁截面為基礎(chǔ)，保持頂板、底板、腹板和梁高的尺寸不變，通過(guò)以0.5 m的步長(zhǎng)，使懸臂板從3 m增加到10 m，亦即將上懸臂板與底板寬度的比值以0.1的步長(zhǎng)從0.6增加至2，取跨中截面3個(gè)控制節(jié)點(diǎn)的翹曲比例系數(shù)，如圖11所示。

圖11 懸臂板寬度對(duì)翹曲比例系數(shù)的影響Fig.11 Effect of the width of the cantilever plate on distortion ratio

如圖11所示，可以明顯看出①號(hào)點(diǎn)和②號(hào)點(diǎn)有著類似的變化軌跡，翹曲比例系數(shù)隨懸臂板寬度比的增大而增大，但①號(hào)點(diǎn)處的λ要明顯大于其他控制點(diǎn)。這是因?yàn)閼冶郯宓脑龃髮?dǎo)致截面約束系數(shù)μ減小，使①號(hào)點(diǎn)處所占翹曲應(yīng)力越來(lái)越大；③號(hào)點(diǎn)隨著懸臂板寬度比的增大而呈減小趨勢(shì)，但也一直保持著一定的比例。所以懸臂板對(duì)截面的約束扭轉(zhuǎn)效應(yīng)不容忽視，且懸臂越寬越予以重視。

3.3 腹板傾角的影響

以圖3箱梁截面為基礎(chǔ)，保持懸臂板、底板和梁高尺寸及其組件厚度不變的情況下，改變箱梁上頂板寬度來(lái)改變腹板傾角。假設(shè)箱梁頂寬從5.02 m增加至11.22 m，步長(zhǎng)為0.31 m，則腹板傾角(腹板和Y軸的夾角)以5°的步長(zhǎng)從0°增加至45°，通過(guò)ANSYS數(shù)值模擬分析，取跨中3個(gè)控制節(jié)點(diǎn)處的翹曲應(yīng)力，如圖12所示。

圖12 翹曲應(yīng)力隨腹板傾角變化曲線Fig.12 Curve of warping stress with web inclination

如圖12所示，隨著腹板傾角的增大，①號(hào)點(diǎn)和②號(hào)點(diǎn)處的翹曲應(yīng)力呈減小的趨勢(shì)，這是因?yàn)殡S著腹板傾角的增大，截面懸臂板越來(lái)越短，從而導(dǎo)致翹曲效應(yīng)減小；③號(hào)點(diǎn)處的翹曲應(yīng)力隨腹板傾角的改變，沒(méi)有明顯的影響。

4 結(jié)論

(1)對(duì)于40 m雙線鐵路簡(jiǎn)支箱梁而言，在偏心荷載引起的集中扭矩在跨中位置處作用時(shí)翹曲雙力矩達(dá)到峰值，但是很快又衰退，且離集中扭矩的位置越遠(yuǎn)，翹曲雙力矩越小，甚至接近于0，根據(jù)翹曲應(yīng)力公式可知，在翹曲雙力矩峰值處，翹曲應(yīng)力達(dá)到最大值。

(2)40 m箱梁在單線偏心荷載作用下，跨中截面約束扭轉(zhuǎn)翹曲效應(yīng)最為明顯，且懸臂端、頂板和腹板的交點(diǎn)和底板與腹板的交點(diǎn)是整個(gè)截面的控制點(diǎn)，其中懸臂端的翹曲應(yīng)力最大，翹曲效應(yīng)最明顯，且此點(diǎn)的約束扭轉(zhuǎn)正應(yīng)力大概占活載彎曲正應(yīng)力的9.16%。

(3)3個(gè)控制節(jié)點(diǎn)處的翹曲比例系數(shù)大小都隨著高寬比的增大而減小，當(dāng)高寬比達(dá)到1.0及其以后時(shí)，三點(diǎn)處的翹曲比例系數(shù)都趨于穩(wěn)定，且3個(gè)值都很接近。并且在高寬比為0.2～1.0時(shí)，底板與腹板交接處的翹曲比例系數(shù)減小的幅度最大。

(4)懸臂板越長(zhǎng)，懸臂端部的翹曲應(yīng)力值越大，但頂板與腹板交接處的翹曲比例系數(shù)并沒(méi)有隨懸臂板寬度的增加有明顯的增長(zhǎng)，而底板和腹板的交點(diǎn)則呈減小的趨勢(shì)；隨著腹板傾角的增大，懸臂端部和頂板與腹板交接處的翹曲應(yīng)力呈現(xiàn)減小的趨勢(shì)，但對(duì)底板與腹板交接處的翹曲應(yīng)力影響不大。