軸對稱缺陷軸壓圓柱殼穩定性分析剛度折減方法

白 旭，李金華

(1.江蘇科技大學 船舶與海洋工程學院，江蘇 鎮江 212003；2.齊魯工業大學（山東省科學院），山東省科學院海洋儀器儀表研究所，山東 青島 266061)

0 引 言

圓柱殼結構具有特殊的幾何構型，對于軸壓、徑壓、扭轉以及組合載荷均具有很好的承載作用，在船舶與海洋工程等各類領域中都有十分廣泛的應用。圓柱殼的主要失效模式為失穩，針對其失穩穩定性問題，特別是軸壓作用下的圓柱殼失穩載荷和模態，一直是學者研究最為活躍的課題之一[1]。

早期針對軸壓作用下薄壁圓柱殼的穩定性試驗表明結構實際的失穩承載能力和理論上理想的完善殼體相比較小，原因就在于初始缺陷的存在會引起軸壓薄壁圓柱殼臨界失穩載荷很大程度的折減。祝恩淳等[2]針對軸壓作用下薄壁圓柱殼的試驗數據，采取統計分析的方法給出了結構失穩應力的經驗計算公式。Lauren Kougias[3]采用有限元數值方法研究了殼體不圓度對軸壓圓柱殼穩定性的影響，認為圓柱殼不圓度與殼體厚度相當時，臨界承載能力降低可達75%。Muggeridge等[4]研究認為局部軸對稱缺陷對圓柱殼失穩臨界載荷的影響很大。龔友根等[5]研究凹坑形式的軸對稱缺陷對軸壓圓柱殼失穩承載能力的影響。王小明[6]研究了縱骨對環肋圓柱殼殼板穩定性的影響。

一系列的研究表明，研究分析方法對于問題的適用性以及結果準確度存在突出的影響。針對圓柱薄殼結構的失穩問題，Croll 等[7-8]提出的剛度折減方法（Reduced Stiffness Method，RSM）在一定程度上理論值可以與實驗值很好的吻合，隨即引發了基于RSM 開展不同類型以及不同承載的薄壁殼體結構失穩載荷的研究。Rossana C.Jaca 等[9]應用RSM 法研究了風載荷作用下圓柱殼結構的失穩失穩問題，認為采用RSM 方法得到的失穩下界與非線性分析結果較為一致。Hongtao Wang 等[10]采用RSM 方法對圓柱殼體結構的失穩承載能力進行了優化研究，認為在給定材料和幾何參數的范圍內，改善了失穩臨界載荷。Eduardo M.Sosa 等[11]基于RSM 方法分析了風載荷作用下含有初始缺陷的圓錐殼結構失穩臨界載荷。Xu Bai 等[12]分析了剛度折減對環肋圓柱殼承載能力的影響，研究結果表明周向薄膜剛度對圓柱殼的穩定性影響最大，軸向的彎曲剛度對圓柱殼穩定性的影響較小。

在現有基礎上，本文采取RSM 針對具有軸對稱缺陷的軸壓圓柱殼的穩定性進行研究。

1 軸壓下完善圓柱殼的失穩載荷

1.1 失穩載荷

軸壓作用下完善薄壁圓柱殼模型如圖1 所示。圓柱殼兩端自由支持在剛性周界，設定長度為l，壁厚為t，半徑為 r，均勻軸向壓力為 p，材料的彈性模量為E，位移為(U,V,W)。

依據薄殼理論，圓柱殼失穩前的應力狀態下：

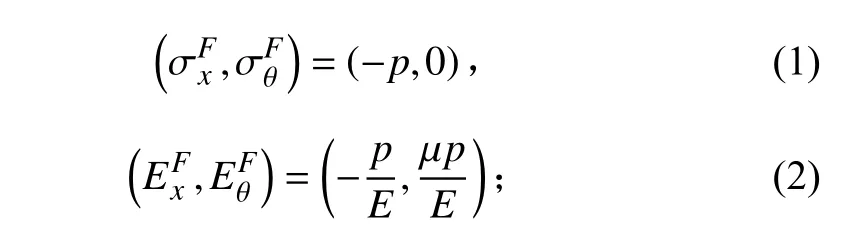
失穩后的平衡狀態為：

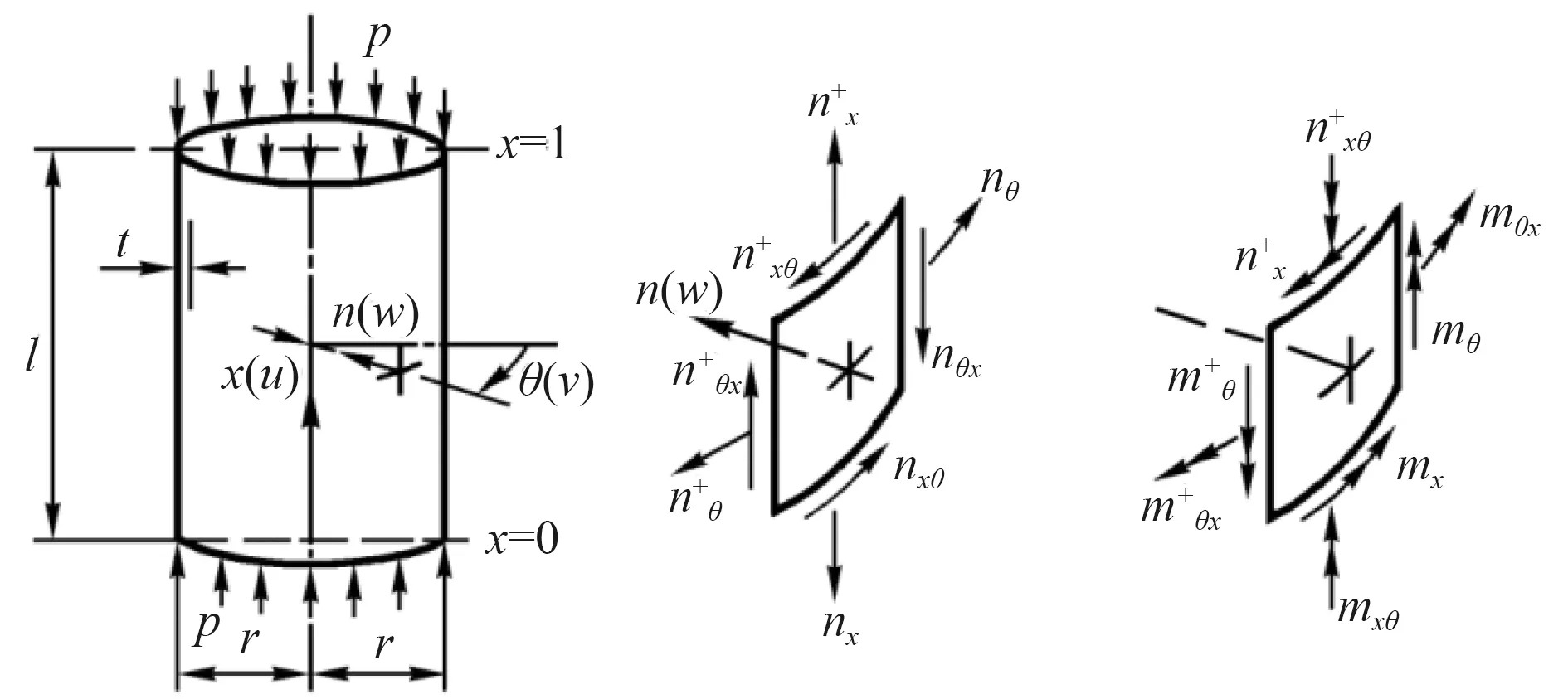
圖1 軸壓完善圓柱殼模型Fig.1 Perfect cylindrical shell model under axial compression

失穩后，總應力、應變、彎矩、轉角可以寫為：

其中公式右邊第1項為失穩前，第2項為失穩后相對增量。

將應變、應力分成線性項部分(ε′x,ε′θ,ε′xθ)，(n′x,n′θ,n′xθ)和二次項部分(ε′′x,ε′′θ,ε′′xθ)，(n′′x,n′′θ,n′′xθ)，忽略高階項，則圓柱殼總勢能為：

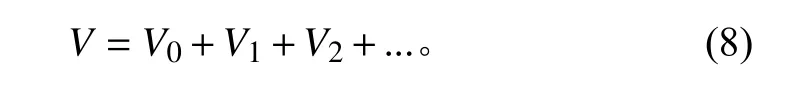
其中：

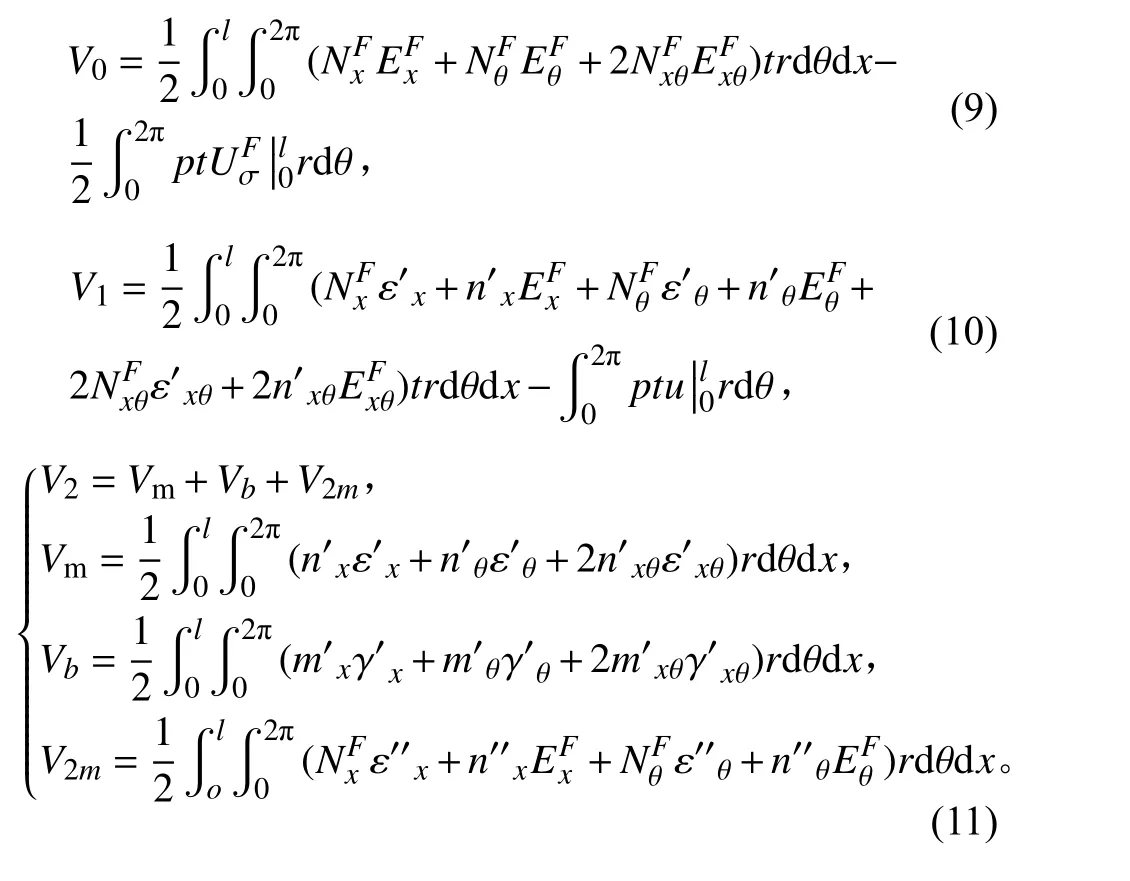
圓柱殼位移選取為：

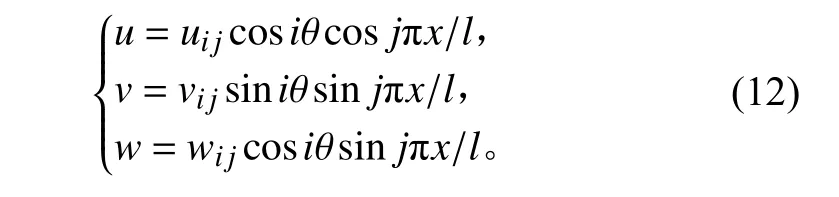
其中：i 為圓周方向的波數；j 為軸線方向的半波數；uij，vij，wij為任意常數。

依據文獻[13]中圓柱殼幾何方程和胡克定律，可以得到：

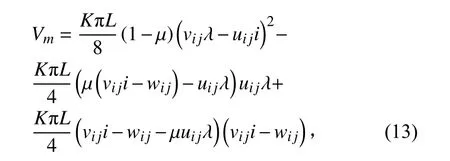
其中：λ=jπ/L，L=l/r。

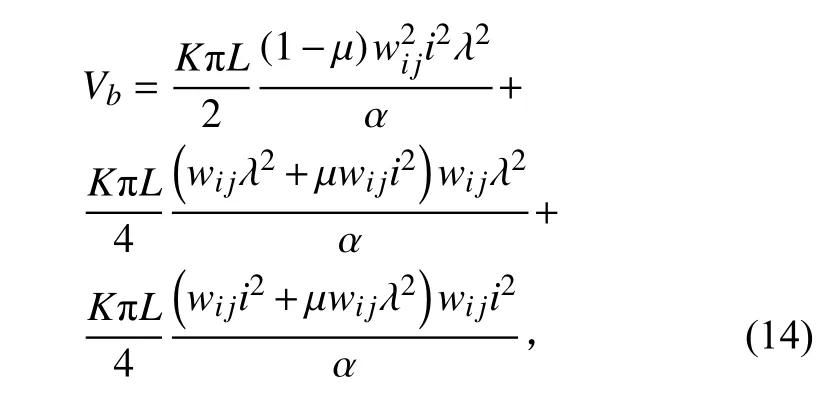
其中：α=12R2，R=r/t。

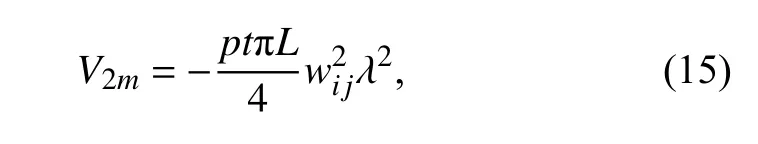
由于總勢能二次項部分在任意條件下的偏導為0，因而可轉化為特征值方程問題:

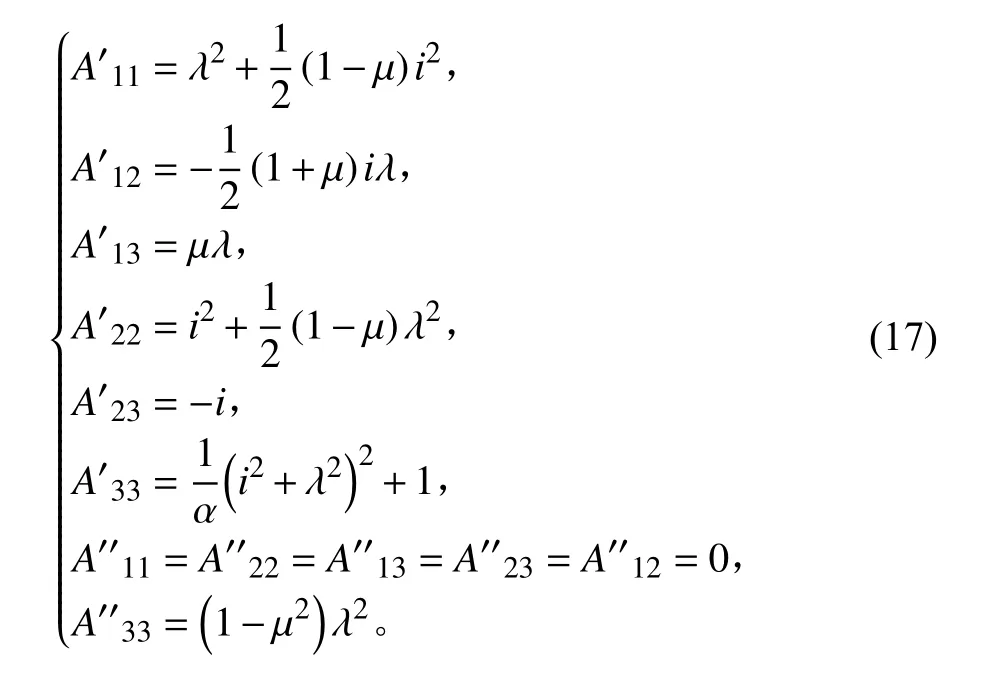
其中：Λ=p/E。

式（16）存在任意解的條件是系數行列式為0，因而

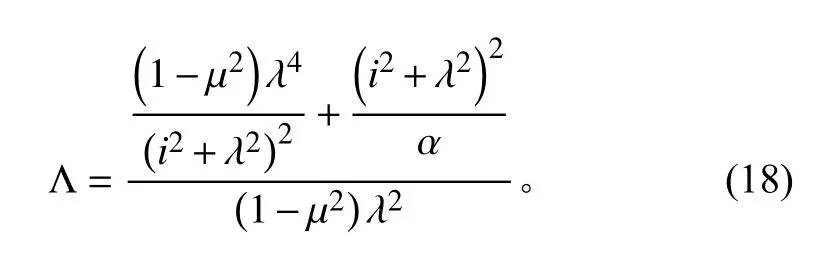
1.2 結果分析

圖2 給出了應用式（18）得到的軸壓作用下完善圓柱殼結構的失穩載荷（L=2.88，R=250，t=5，以下計算均以此參數為基礎），可以看出軸壓圓柱殼存在多種失穩模態。

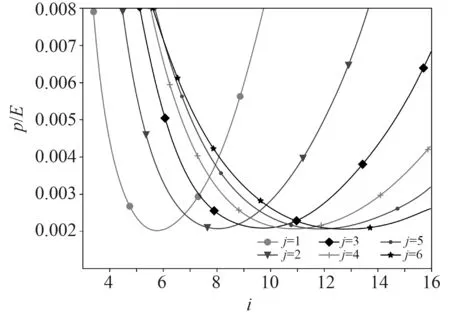
圖2 軸壓圓柱殼失穩載荷圖譜Fig.2 Instability load spectrum of axial compression cylindrical shell

從圖3 和圖4 中可以看出，承受軸向壓力圓柱殼的失穩載荷僅與圓柱殼半徑與厚度的比R 有關，與長度和半徑的比L 無關。因此在式（18）中，求其最小值，得

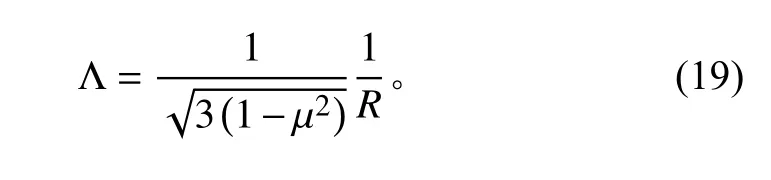
與經典彈性臨界應力公式相同。

2 軸壓圓柱殼的剛度折減分析

依據式（11），軸壓完善圓柱殼失穩總勢能中的V2項可以表述為：

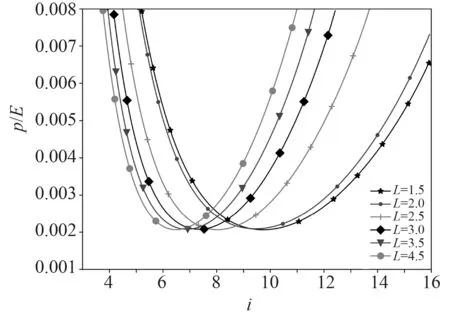
圖3 不同L 下的失穩載荷Fig.3 Instability load at different L

圖4 不同R 下的失穩載荷Fig.4 Instability load at different R

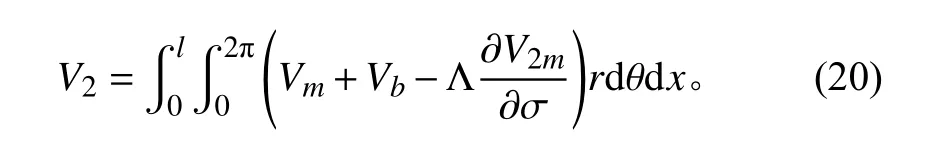
通過殼體的穩定條件，將軸向壓力下圓柱殼穩定性問題轉化為求解特征方程的特征值問題：

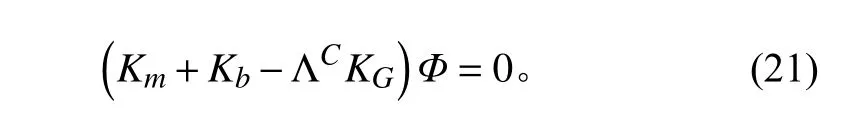
式中：Km和 Kb分別是薄膜剛度矩陣和彎曲剛度矩陣；KG幾何剛度矩陣；參數 Λc是特征值而向量Φ是特征向量，對應于圓柱殼的失穩載荷和失穩模態。

當圓柱殼各剛度折減時，式（22）應寫為：

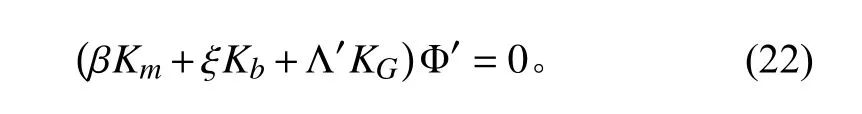
其中：Λ′和Φ′為折減剛度后的新的特征值和特征向量。β為薄膜剛度折減系數（0＜β≤1），ξ 為彎曲剛度折減系數（0＜ξ≤1）。

因此式（18）中的系數將變為：

可得含有折減系數的臨界載荷方程：

通過分析，臨界載荷方程分子的兩項分別代表薄膜剛度和彎曲剛度對臨界載荷的貢獻，在公式（24）中，求其最小值得：

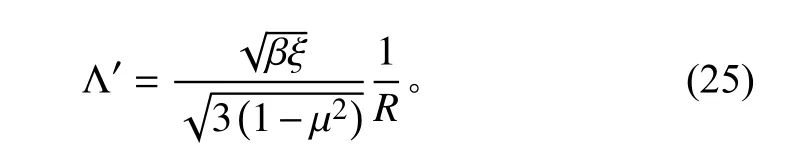
圖5 和圖6 給出了不同剛度折減系數對軸向受壓薄壁圓柱殼失穩載荷的影響。

可以看出，無論是薄膜剛度還是彎曲剛度的降低都會影響軸壓圓柱殼的失穩模態。軸壓圓柱殼失穩時周向波數隨著薄膜剛度的減少而減少，隨著彎曲剛度的降低而增加。

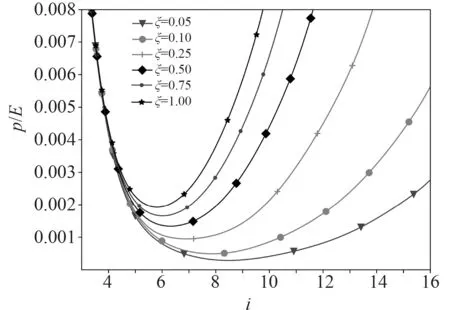
圖5 彎曲剛度折減失穩載荷圖譜Fig.5Instability load spectrum of bending stiffness reduction

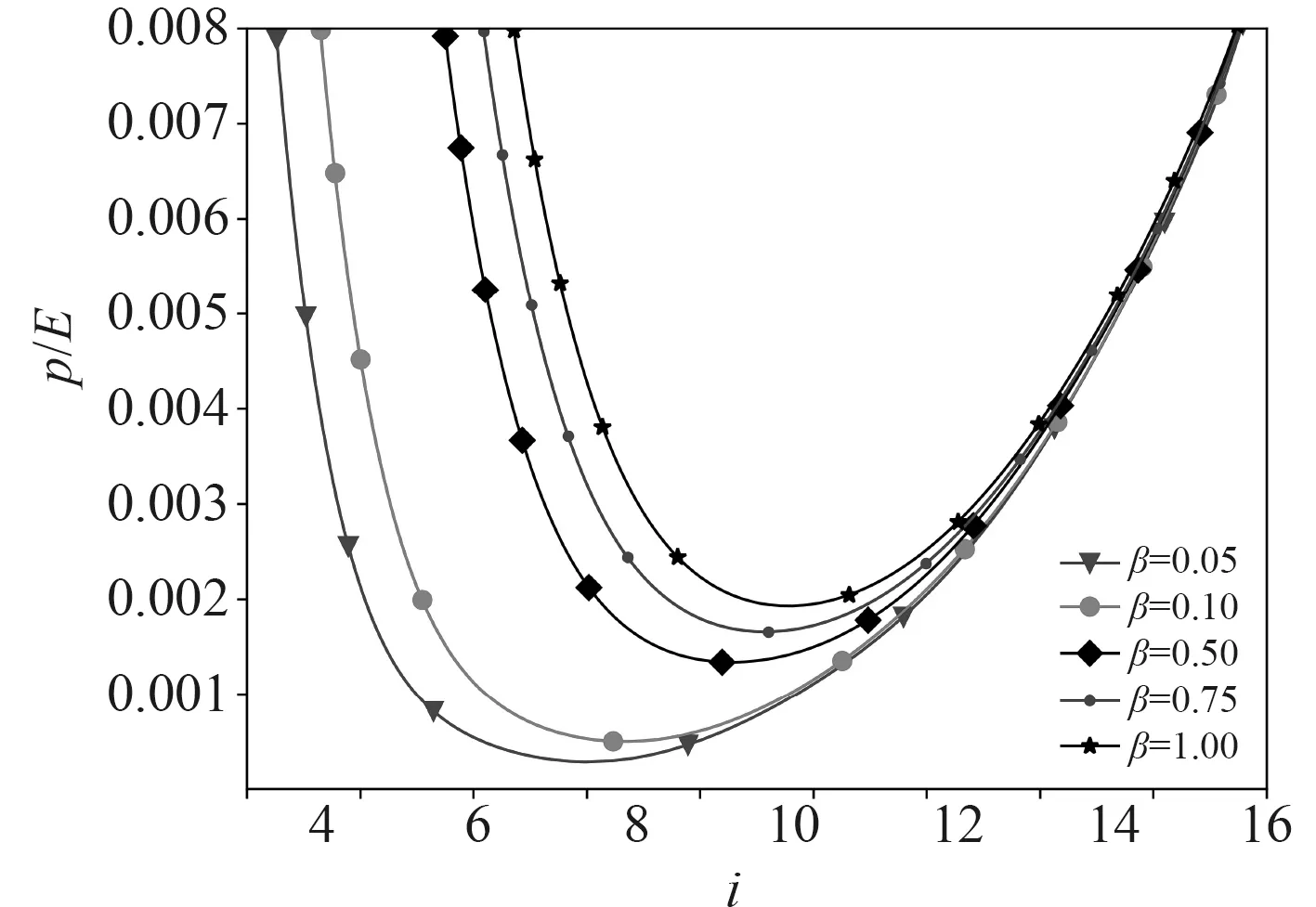
圖6 薄膜剛度折減失穩載荷圖譜Fig.6 Instability load spectrum of film stiffness reduction

3 含軸對稱缺陷圓柱殼失穩分析

3.1 基于RSM 的失穩載荷計算

含軸對稱初始缺陷圓柱殼模型如圖7 所示。設定長度為l，半徑為 r，初始缺陷的幅值為 w0，缺陷的曲率為ρ，靜水壓力為 p，殼板的厚度為t。

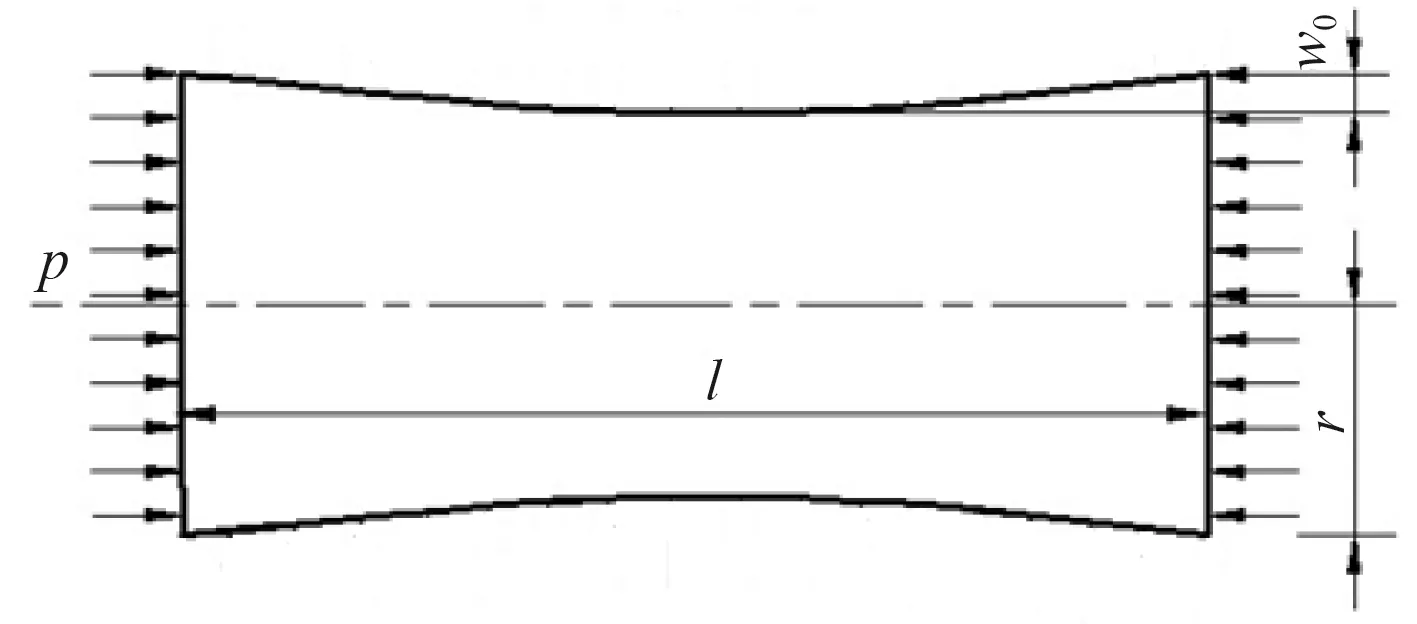
圖7 含軸對稱缺陷軸壓圓柱殼模型Fig.7 Axially compressed cylindrical shell model with axisymmetric defects

缺陷幅值相對于半徑為小量，忽略對圓柱殼應力分布的影響，殼體失穩前應力和應變仍然為式（1）和式（2），而幾何方程如下：

因此相對于完善殼體，式（13）～式（15）分別表述為：

其中：α=12R2，R=r/t。

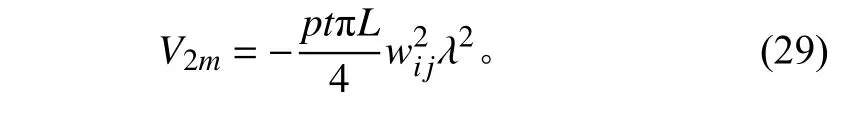
根據殼體穩定條件得到系數行列式的系數為：

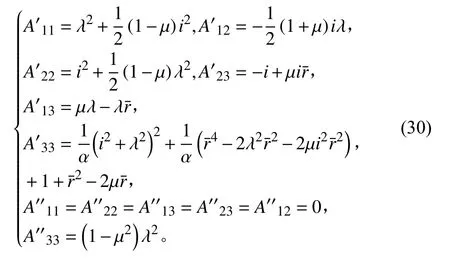
得含軸對稱缺陷的軸壓圓柱殼失穩臨界載荷：

3.2 軸對稱缺陷對失穩載荷的影響

為便于分析初始缺陷對薄膜剛度和彎曲剛度的影響，令

式（31）可寫為：

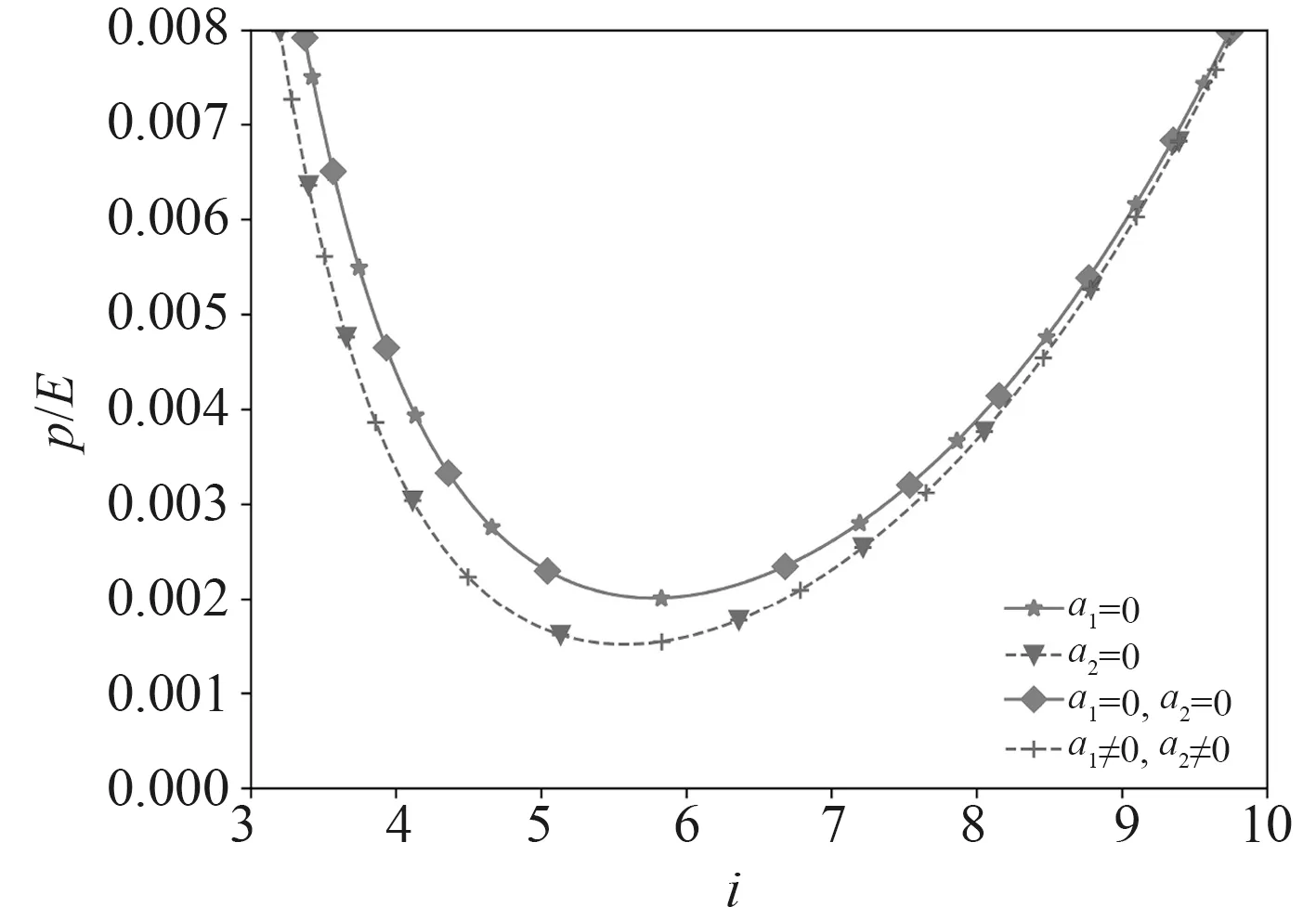
圖8 缺陷在軸壓圓柱殼失穩的影響Fig.8 Effect of defects on the instability of cylindrical shells under axial compression

由圖8 中可以看出，a2對圓柱殼的影響很小，可以忽略不計，因此將式（34）簡化為：

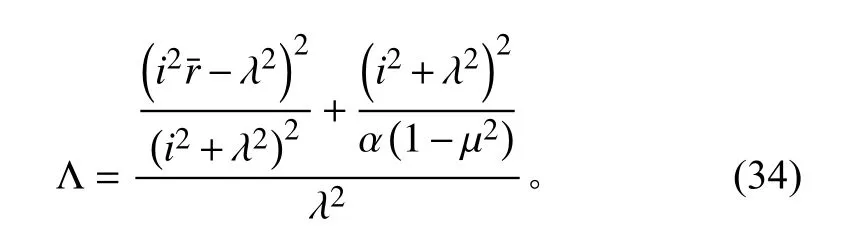
從式（34）可以看出，軸對稱缺陷是經過圓柱殼失穩時軸向波數二次方放大，所以很小的初始缺陷將會對圓柱殼的穩定承載能力產生較大影響。

由圖9 可以看出，與無缺陷時軸向受壓圓柱殼的失穩模式不同，當縱向失穩波數是1 時，含軸對稱初始缺陷的軸壓受壓圓柱殼的失穩載荷有最小值。比較式（34）和式（25）可得含軸對稱缺陷圓柱殼承受軸向均勻壓力時，薄膜剛度折減系數與軸對稱初始缺陷的關系為：

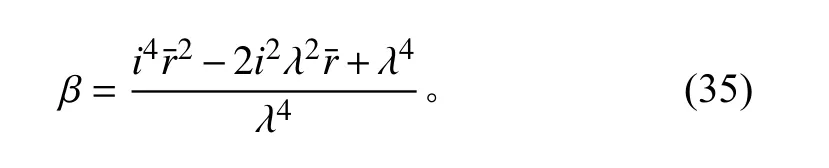
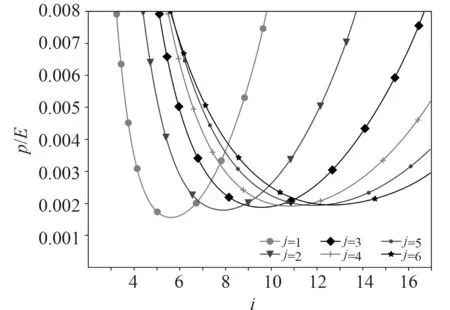
圖9 含軸對稱缺陷軸壓圓柱殼的失穩臨界載荷圖譜Fig.9 Instability critical load spectrum of axially compressed cylindrical shells with axisymmetric defects

4 結 語

采用RSM 方法針對軸壓載荷作用下完善圓柱殼以及具有軸對稱缺陷圓柱殼結構的穩定性進行了分析，主要結論如下：

1）軸壓作用下完善圓柱殼結構的失穩載荷與半徑、厚度的比有關，與長度、半徑比無關。

2）軸壓圓柱殼結構的薄膜剛度、彎曲剛度均影響其失穩模態，失穩周向波數隨著薄膜剛度的減少而減少，隨著彎曲剛度的降低而增加。

3）由于軸對稱缺陷通過圓柱殼失穩的軸向波數二次方放大來影響薄膜剛度，故對其臨界承載能力影響很大。