基于PSASP的九節點電力系統暫態穩定分析

摘要：電力系統暫態穩定分析的主要目的是檢查電力系統在受到大的擾動情況下，如發生故障、切機、切負荷、重合閘操作等，各發電機機組間是否能保持同步運行，且運行電壓和頻率是否在規定范圍內，若是，則表明該系統在這一大的擾動下運行是暫態穩定的。現將九節點電力系統中的各元件模型，根據元件間拓撲關系形成全系統模型，并通過PSASP仿真，以潮流解為初值，模擬相應的擾動類型，求系統擾動下的數值解，根據母線電壓和發電機功角判斷該電力系統在大的擾動下運行的暫態穩定性。

關鍵詞：暫態穩定;PSASP;母線電壓;發電機功角

0 引言

電力系統暫態穩定性是保證電力系統正常運行必須考慮的重要問題。當電力系統受到大的擾動時，各發電機組間需要保持同步運行，且運行電壓和頻率需控制在規定范圍內，以保證電力系統的穩定運行。本文以九節點電力系統在受到擾動時的運行情況為模型，進行PSASP仿真，根據輸出圖形直觀判斷電力系統的暫態穩定性。

1 潮流計算

潮流計算是指在給定電力系統網絡拓撲、元件參數和發電、負荷參量條件下，計算有功功率、無功功率及電壓在電力網中的分布情況。

現在通常用牛頓法進行潮流計算，其原理：在直角坐標下，節點功率表示為Pi+jQi;節點電壓表示為ei+jfi。

對于PQ節點，其節點有功功率平衡、節點無功功率平衡公式為：

ΔPi=Pis-Pi=0 ? ?ΔQi=Qis-Qi=0

式中：Pis和Qis為第i個PQ節點給定的有功功率和無功功率;Pi和Qi為第i個節點的有功功率和無功功率。

對于PV節點，其節點有功功率平衡、節點電壓平衡公式為：

ΔPi=Pis-Pi=0 ? ?ΔVi 2=Vis 2-Vi 2=0

式中：Pis和Vis為第i個PV節點給定的有功功率和電壓幅值;Pi為節點有功功率;Vi為節點電壓。

在極坐標下，對于每個PQ節點及PV節點，都可以列寫一個有功功率不平衡量方程式ΔPi=0，而對于每一個PQ節點還可以列寫一個無功功率不平衡量方程式ΔQi=0。

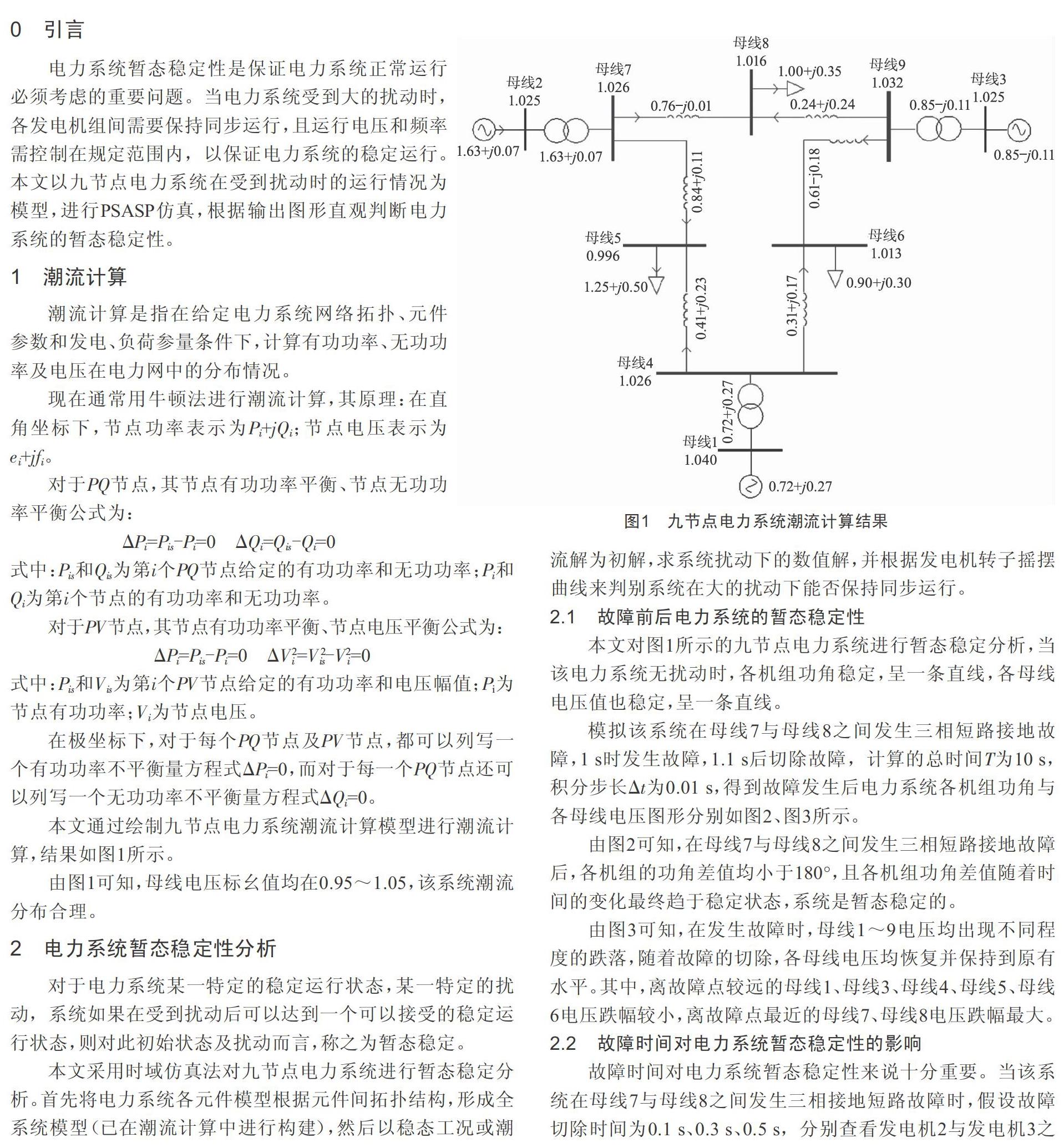
本文通過繪制九節點電力系統潮流計算模型進行潮流計算，結果如圖1所示。

由圖1可知，母線電壓標幺值均在0.95～1.05，該系統潮流分布合理。

2 電力系統暫態穩定性分析

對于電力系統某一特定的穩定運行狀態，某一特定的擾動，系統如果在受到擾動后可以達到一個可以接受的穩定運行狀態，則對此初始狀態及擾動而言，稱之為暫態穩定。

本文采用時域仿真法對九節點電力系統進行暫態穩定分析。首先將電力系統各元件模型根據元件間拓撲結構，形成全系統模型（已在潮流計算中進行構建），然后以穩態工況或潮流解為初解，求系統擾動下的數值解，并根據發電機轉子搖擺曲線來判別系統在大的擾動下能否保持同步運行。

2.1 ? ?故障前后電力系統的暫態穩定性

本文對圖1所示的九節點電力系統進行暫態穩定分析，當該電力系統無擾動時，各機組功角穩定，呈一條直線，各母線電壓值也穩定，呈一條直線。

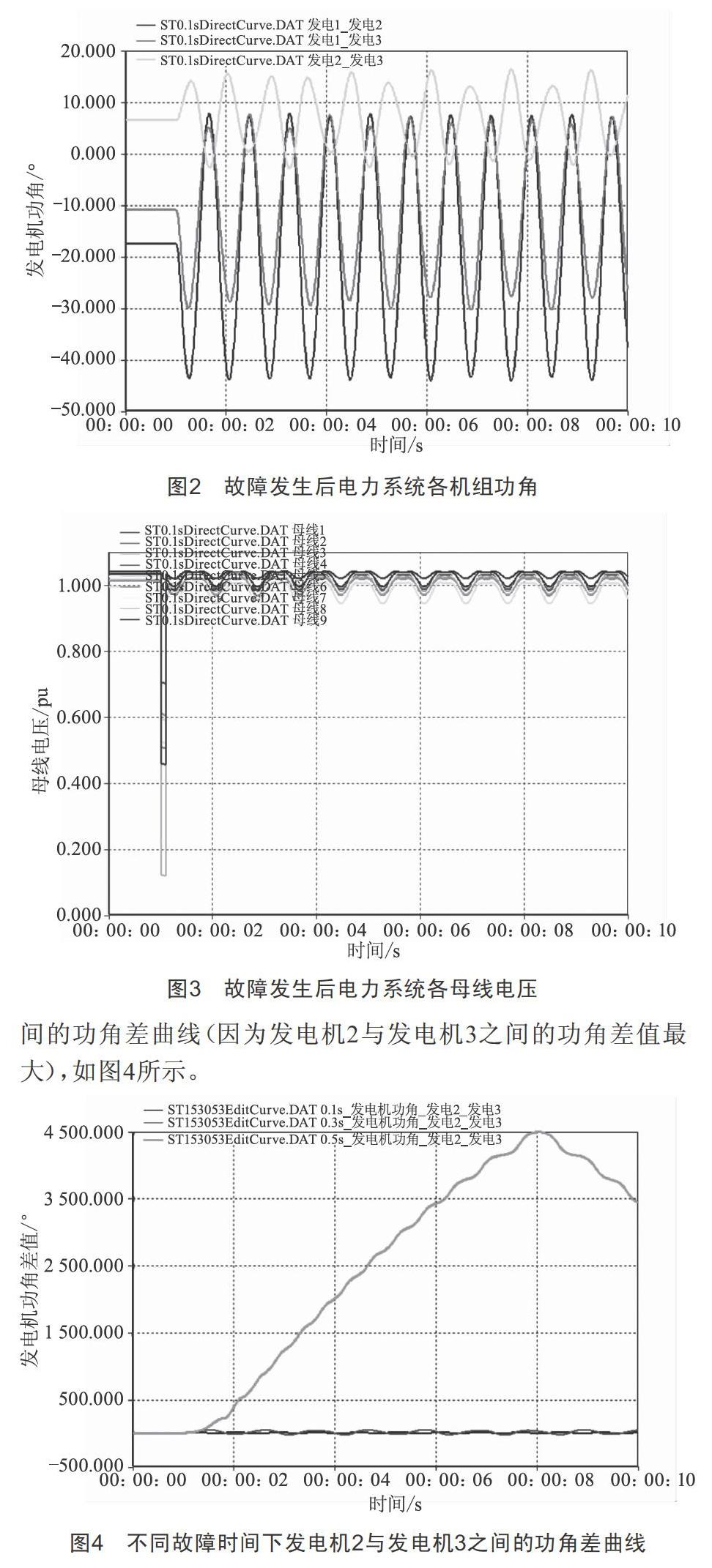
模擬該系統在母線7與母線8之間發生三相短路接地故障，1 s時發生故障，1.1 s后切除故障，計算的總時間T為10 s，積分步長Δt為0.01 s，得到故障發生后電力系統各機組功角與各母線電壓圖形分別如圖2、圖3所示。

由圖2可知，在母線7與母線8之間發生三相短路接地故障后，各機組的功角差值均小于180°，且各機組功角差值隨著時間的變化最終趨于穩定狀態，系統是暫態穩定的。

由圖3可知，在發生故障時，母線1～9電壓均出現不同程度的跌落，隨著故障的切除，各母線電壓均恢復并保持到原有水平。其中，離故障點較遠的母線1、母線3、母線4、母線5、母線6電壓跌幅較小，離故障點最近的母線7、母線8電壓跌幅最大。

2.2 ? ?故障時間對電力系統暫態穩定性的影響

故障時間對電力系統暫態穩定性來說十分重要。當該系統在母線7與母線8之間發生三相接地短路故障時，假設故障切除時間為0.1 s、0.3 s、0.5 s，分別查看發電機2與發電機3之間的功角差曲線（因為發電機2與發電機3之間的功角差值最大），如圖4所示。

由圖4可知，在故障時間為0.1 s與0.3 s時，各機組的功角差值均小于180°，且各機組功角差值隨著時間的變化最終趨于穩定狀態，系統是暫態穩定的。而當故障時間為0.5 s時，發電機2與發電機3之間的功角差值大于180°，系統運行失去穩定性。

2.3 ? ?故障極限切除時間的確定

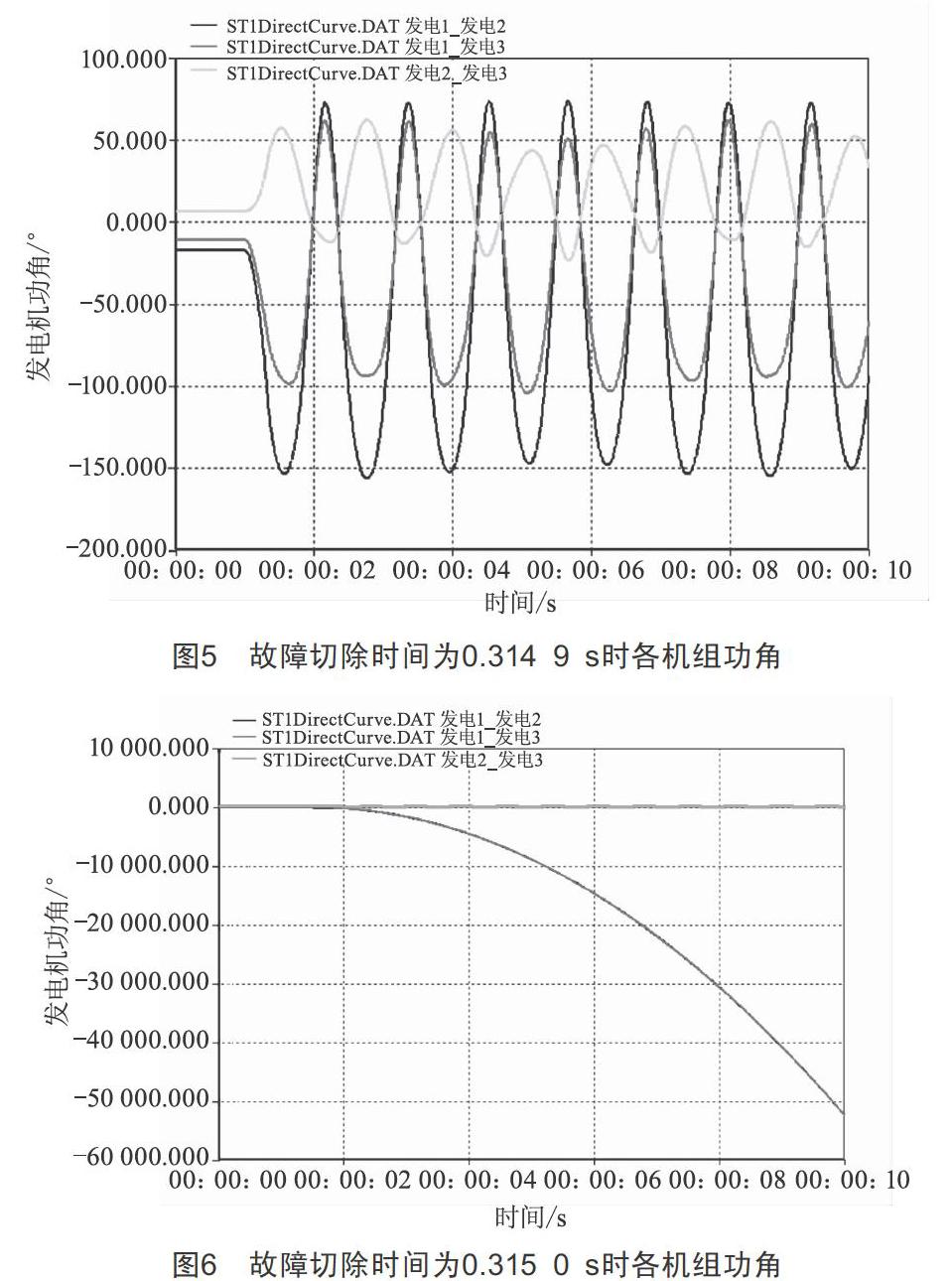
由2.2可知，不同的故障切除時間對電力系統的暫態穩定性影響很大，為此，要是電力系統工作在穩定狀態下，需要確定故障切除時間的極限值。當故障切除時間為0.314 9 s與0.315 0 s時各機組的功角曲線如圖5、圖6所示。

由圖5、圖6可知，當故障切除時間為0.314 9 s時，該系統運行能夠保持穩定，當故障切除時間為0.315 0 s時，該系統運行將失去穩定。因此，該電力系統故障極限切除時間為0.314 9 s。

3 結語

本文運用PSASP對三機組九節點電力系統進行了潮流計算與暫態穩定分析。在無擾動工況下，該電力系統能夠保持穩定運行;當電力系統受到大的擾動時，距離擾動較遠的母線受到的影響較小，距離擾動越近的母線受到的影響越大;故障切除時間越短，各機組之間的功角差值越小，系統就越穩定;當故障切除時間超過0.315 0 s時，系統將失去穩定，需要采取另外的措施來保證系統的正常運行。

[參考文獻]

[1] 倪以信，陳壽孫，張寶霖.動態電力系統的理論與分析[M].北京：清華大學出版社，2002.

[2] 劉天琪.現代電力系統分析理論與方法[M].北京：中國電力出版社，2007.

收稿日期：2020-08-07

作者簡介：李愷（1993—），男，山東高密人，助理工程師，從事低壓配電工作。