水輪的混沌現象分析及數值仿真

王賀元, 張 熙

(沈陽師范大學 數學與系統科學學院, 沈陽 110034)

隨著洛倫茲非線性動力系統的面世,混沌現象越來越受關注,洛倫茲方程和類洛倫茲方程作為非線性動力系統的代表,引起了國內外許多學者的普遍關注,并對其進行了深入的研究。洛倫茲方程是在局部區域小氣候的背景下建立起來的簡化的三維非線性微分方程組,因為全球氣候變化的物理背景相當復雜,無法進行大量實驗,從而洛倫茲把其簡化為一種簡單的力學裝置,從中給出了對應的洛倫茲方程[1-2]。

洛倫茲系統開啟了混沌研究的先河,基于洛倫茲系統的混沌研究可分為2種獨立的方法,一種是方程解的性質研究,用計算機進行數值模擬[1-5],另一種是混沌水輪物理實驗。幾十年來,先后有Miroslav Kolar、Leslie E. Matson、Ashish Bhatt等致力于混沌水輪實驗研究,從數學角度討論了水輪的混沌現象[6-8],但是此方面的中文文獻沒有涉及,而且沒有將物理現象與數學機理聯系起來。本文討論了水輪混沌現象的產生與發展過程,并聯系實際物理現象,對水輪的混沌旋轉問題給出合理解釋。

1 混沌水輪裝置簡介與運動特征分析

如圖1所示,混沌水輪裝置與古代的水車相似,水輪頂端有恒定水流注入掛在輪邊緣的水杯中。每只杯底部均有一小孔能恒定地出水。如果上面的水流速度很慢,頂部水杯內水量少,因而不能克服輪軸摩擦力,水輪不會轉動;如果水流加快,隨著頂部水杯內水的增多,帶動水輪開始勻速旋轉;隨著水流繼續加大,旋轉便呈混沌狀態,轉動的方向和速度會因系統內在的非線性而出現復雜的運動特性。

圖1 混沌水輪實驗裝置示意圖Fig.1 Schematic diagram of chaotic water wheel experimental device

2 混沌水輪的數學模型及特性

文獻[6]經過一系列物理推導,得到了混沌水輪簡化的動力學方程組為[9]

(1)

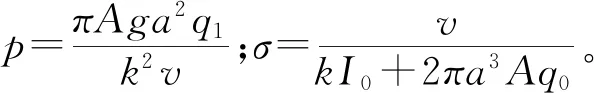
類洛倫茲系統(1)具有對稱性,即在變換(X,Y,Z)→(-X,-Y,Z)下具有不變性,即系統(1)關于Z軸具有對稱性,且這種對稱性對所有的系統參數均成立[10]。

3 平衡點及局部穩定性

3.1 平衡點

3.2 穩定性

|λE-J2|=λ3+(σ+2)λ2+(p+σ)λ+2σ(p-1)=0

(2)

此時p>1。

當p繼續變大時,勢必出現轉折點,當p超過此值,特征根將出現復根,此時特征方程出現二重根,設轉折點對應的參數p為p1。

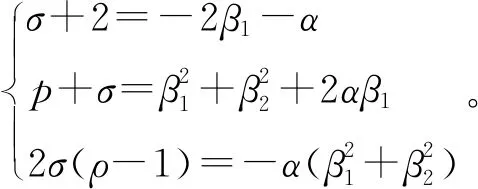
當p1

當p>p2時,特征方程存在實部為正的虛根,故此時平衡點不穩定,存在Hopf分岔。

4 全局穩定性分析

5 系統的動力學行為數值仿真及其分析

本節對系統(1)的動力學行為進行數值仿真。固定系統參數σ=5,隨著p的增大,混沌水輪方程組的動力學行為發生了一系列變化,如出現了Hopf分岔和混沌等非線性現象。本文在MATLAB數學軟件中采用龍格-庫塔算法,對系統(1)求數值解,進而畫出仿真圖,并以此揭示系統(1)的混沌學行為[15]。

圖2給出了當σ=5,0≤p≤350時的分岔圖,圖3給出了上述范圍內的最大李雅普諾夫指數。當p1=1.058 45時系統(1)開始發生分岔,當p2=15時產生混沌,混沌區在117.559≤p≤132時有一個較明顯的周期窗口。

圖2 當σ=5,ρ=66時狀態變量y的分岔圖

圖3 當σ=5,ρ=66時最大Lyapnov指數圖

系統(1)在進入混沌狀態以后,吸引子將出現復雜的蝴蝶型,龐家萊截面也會隨之變得復雜。如圖4和圖5所示,取σ=5,ρ=66>15,得到吸引子和龐加萊截面,此時系統正處于混沌態。

圖4 當σ=5,ρ=66時吸引子圖Fig.4 Subgraph of attraction when σ=5 and ρ=66

圖5 當σ=5,ρ=66時龐加萊截面Fig.5 Poincaré cross section when σ=5 and ρ=66

取σ=5,ρ=16,系統(1)的功率譜和返回映射如圖6～圖7所示,此時系統已經進入混沌狀態。

圖6 當σ=5,ρ=66時的功率譜Fig.6 Power spectrum when σ=5 and ρ=66

圖7 當σ=5,ρ=66時的返回映射Fig.7 Return mapping when σ=5 and ρ=66

6 結 論

本文通過對系統(1)解的研究和數值仿真,揭示了水輪模型混沌的數學機理,結合水輪實驗的物理現象,解釋了水輪的混沌旋轉現象。當實驗裝置輪軸間摩擦力固定時,σ隨之固定,隨著注水速度的增大,p隨之增大。當015時,系統(1)進入混沌狀態,水輪轉動的角速度和方向都具有隨機性和不可預測性,表現出極為復雜的運動特性。本文將系統的數值仿真結果與物理背景緊密結合,從而揭示了水輪的混沌旋轉現象的數學機理。