差異沉降下機場剛性道面的結構響應與容許沉降分析

金 辰

(同濟大學道路與交通工程教育部重點實驗室 上海 201804)

受地基土類型、壓縮層厚度、填挖高度、地下水變遷等諸多因素影響，跑道地基沉降相差較大，其產生的差異沉降對道面平整度，以及道面結構的穩定性和耐久性有重要影響。我國機場設計規范MH/T 5027-2013規定跑道在設計使用年限內，地基沿縱向差異沉降率應控制在0.1%～0.15%[1]。目前，國內針對跑道地基沉降問題開展了較多研究工作。周正峰等[2]假設道面與地基同步沉降，通過分析一塊水泥板產生最大容許拉應力所對應的地基變形斷面臨界曲率值，認為應控制地基差異沉降的曲率值小于9×10-5m-1。顧強康等[3]通過改變地基反應模量以模擬地基差異沉降，建立9塊板道面結構有限元模型，對差異沉降下的板底最大拉應力進行評估，提出跑道地基縱向差異沉降率應控制在0.1%～0.12%。王廣德等[4]基于跑道道面平坦程度的相關規定，結合相關工程實例分析，建立了跑道地基縱向差異沉降的控制標準。相對而言，這些研究大多針對跑道地基的縱向差異沉降，而對橫向差異沉降的研究較少，且大多集中于小范圍地基沉降下的道面力學響應分析，而對大范圍的地基實際沉降形態下的道面結構響應分析較少。

為此，本文針對不同跑道寬度，建立道面結構有限元模型，對地基橫向差異沉降下的道面結構力學響應進行分析，并提出相應的橫向差異沉降容許值。

1 道面結構有限元模型

1.1 模型幾何特征及材料參數

本文以西南某機場為工程依托，分析3種跑道寬度，即30，45，60 m，分別對應飛行區3C、4E和4F等級。采用ABAQUS軟件對上述3種跑道寬度分別建立模型，取單塊板尺寸為5 m×5 m，3個模型在跑道橫斷面及縱斷面方向的水泥板數量分別為6×3塊、9×3塊、12×3塊，板間接縫寬8 mm。假定道面各結構層為連續均質、各向同性的線彈性材料，道面結構和材料參數采用該機場的實際參數，列于表1。模型兩側約束水平方向位移，模型底部約束各個方向的位移。

表1 三維有限元模型計算參數

1.2 道面接縫傳荷模擬

為考慮接縫的傳荷作用，在水泥板側面的對應結點設置彈簧單元。由于水泥板側面的結點分為角結點、邊結點和內部結點，按照不同位置結點對接縫剛度的貢獻面積，將接縫的總剛度分配到每個彈簧單元上[5]。在本模型中，板間接縫均布置32個彈簧單元，縱縫及橫縫的彈簧換算單位剛度分別為98.087，413.853 MN/m。

1.3 道面層間接觸模擬

本文參考水泥混凝土路面的層間接觸特征設置道面層間接觸條件。對于基層與地基的接觸特征，敖星等[6]均假定基層與地基為完全光滑接觸，故在本模型中將基層與地基的界面同樣設置為完全光滑。對于面層與基層的接觸特征，在AASHTO路面設計指南中，水泥板與水泥穩定碎石基層的建議摩擦系數為1.8[7]；在我國剛性路面設計中，水泥板與半剛性基層的摩擦系數一般在1.0～2.0[8]。故在本模型中，面層與基層的接觸采用庫侖-摩擦模型，摩擦系數取為1.5。

1.4 地基橫向差異沉降模擬

國內多個機場跑道地基的沉降觀測資料表明，跑道橫斷面沉降具有如下特點：從道面邊線向跑道中心線，沉降逐漸增大，中心點處沉降最大，沉降曲線呈“盆形”[9-10]。因此，本文采用土基中最常見的余弦型沉降曲線模擬跑道橫斷面差異沉降，沉降曲線表達式見式(1)。計算中，地基沉降幅值取5～250 mm，跑道寬度取30，45，60 m。

(1)

式中：y為地基沉降值，mm；x為發生沉降的位置，m；A為地基沉降幅值即最大沉降值，mm；B為跑道寬度，m。

1.5 飛機荷載參數

不同飛行區等級適用于不同的飛機機型，本文針對不同飛行區等級選取了該等級下對道面要求最高的機型作為飛機典型荷載。根據該機場航空量預測數據，3C、4E、4F等級跑道所對應的對道面要求最高的機型分別為B737-700，B777-300和A380-800。

飛機最大起飛質量是飛機滿載起飛前質量，由于降落時飛機耗油等原因，飛機的總質量會小于出航起飛前。此外，飛機在滑跑過程中不可避免地會產生升力，在低速滑行階段，由于速度低，升力系數小，可忽略不計；但當速度較快時，飛機滑跑產生的升力較大，飛機對道面荷載減小。為偏安全考慮飛機荷載對道面的影響，采用飛機最大起飛質量并考慮飛機低速滑行階段，忽略飛機升力的影響。輪印面積按總面積相等的原則假定為矩形，飛機主起落架參數見表2。

表2 飛機主起落架參數

經試算，飛機荷載作用的臨界荷位均位于縱縫中部且與縱縫相切，故分析中飛機荷載均作用于靠近沉降中心的水泥板縱縫中部邊緣。

2 地基橫向差異沉降對道面結構變形的影響

當地基發生60 mm/30 m差異沉降時，在自重作用下道面橫斷面方向各層結構的變形見圖1。

圖1 地基沉降60 mm/30 m時道面結構變形

由圖1可見，當地基發生余弦型不均勻沉降時，水泥板和基層在自重作用下發生跟隨變形，變形曲線均呈“類余弦型”，在地基沉降量最大位置處，各層結構的變形也最大；基層變形與地基沉降基本保持一致，兩者接觸狀態較好；而水泥板最大變形量約為57 mm，在地基沉降量最大位置處的一定范圍內，水泥板與基層出現了分離。

分別統計了跑道寬度30 m，沉降幅值在5～250 mm變化時，道面各層結構在自重和飛機荷載作用下的最大變形量，結果見圖2。由圖2a)可見，在一定的跑道寬度下，水泥板和基層在自重作用下的最大變形量均隨沉降幅值的增大而增大并逐漸趨于穩定。當沉降幅值小于30 mm時，各層的最大變形量與地基沉降幅值相近，各層之間接觸較好；當沉降幅值達到40 mm時，水泥板的最大變形量約為39 mm，小于基層的最大變形量，水泥板與基層出現分離；而沉降幅值達到100 mm時，基層的最大變形量小于地基沉降幅值，兩者也出現了分離，且隨著沉降幅值的繼續增大，水泥板和基層的最大變形量與地基沉降幅值差距越大，分離程度也越大。當飛機通過該區域時，道面將產生附加應力，嚴重時會產生斷板等結構性損壞，因此對地基沉降產生的結構層分離要引起足夠的重視。

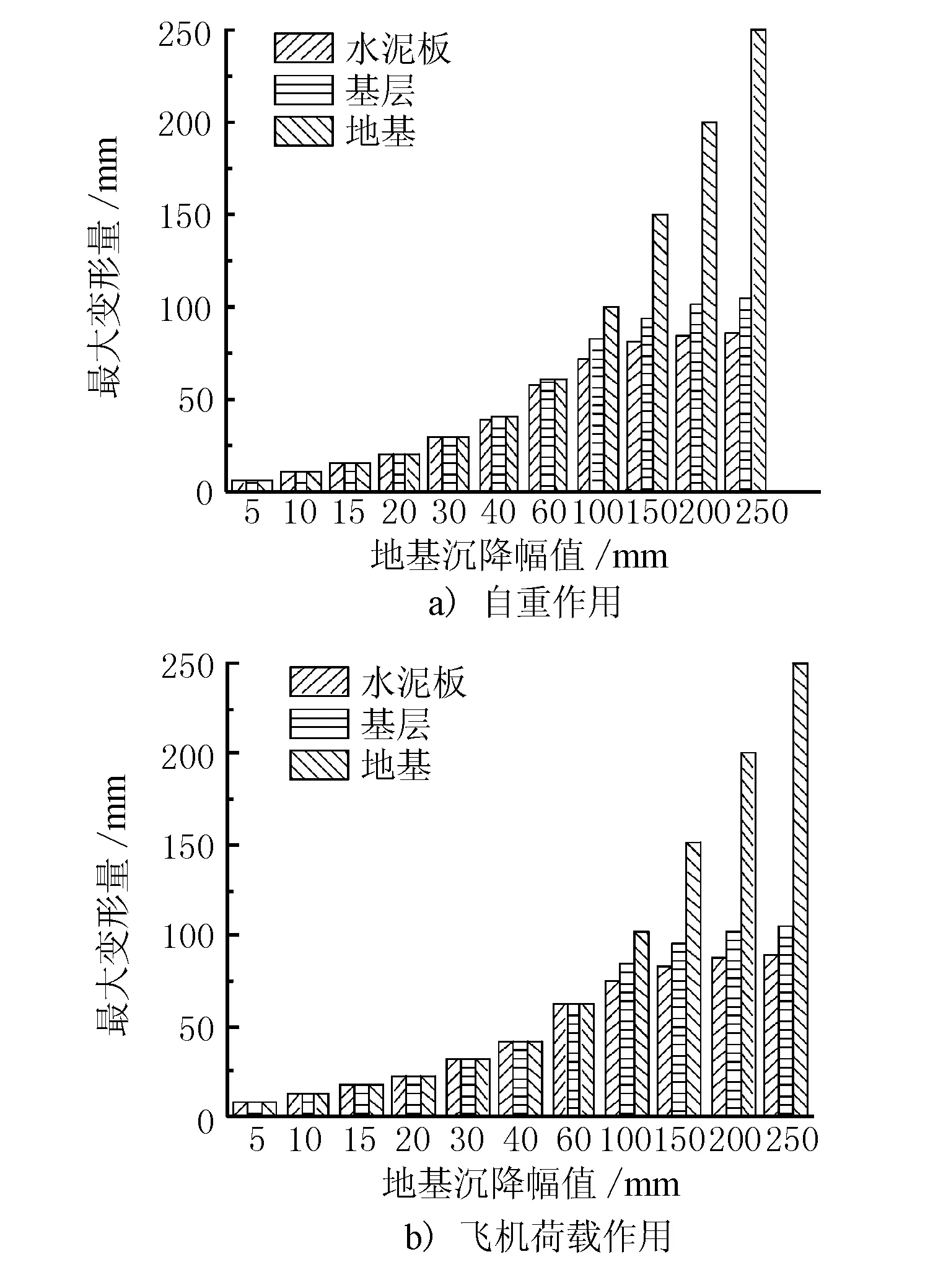
圖2 跑道寬度30 m不同沉降幅值下道面結構最大變形量

由圖2b)可見，在一定的跑道寬度下，水泥板和基層在飛機荷載作用下的最大變形量也隨著沉降幅值的增大而增大，并逐漸趨于穩定。在自重作用下局部分離的結構層，會在飛機荷載作用下重新貼合。如當沉降幅值為60 mm時，在自重作用下水泥板底產生了局部分離，而在飛機荷載作用下水泥板與基層又重新貼合。此時，若板底分離區域存在雨水積聚，在飛機荷載下結構層重新貼合，這樣的循環“泵吸”作用將加劇板底沖刷風險。

當地基沉降幅值為100 mm，跑道寬度在30～60 m變化時，道面各層結構在自重作用下的最大變形量見圖3。

圖3 地基沉降幅值100 mm不同跑道寬度下道面結構最大變形量

由圖3可見，在相同地基沉降幅值下，跑道寬度越大，水泥板和基層在自重作用下的最大變形量也越大，且各層間的分離程度越小。當跑道寬度從30 m變化到60 m時，水泥板與基層的分離程度從約10 mm降至約5 mm，基層與地基的分離程度從約17 mm降至約3 mm。跑道寬度越大，道面結構在自重作用下的沉降跟隨性越好。

3 地基橫向差異沉降對道面力學特性的影響

當地基發生30 mm/30 m差異沉降時，在自重作用下水泥板底部和基層底部的橫向應力沿跑道橫斷面方向的分布見圖4，其中正值表示受拉，負值表示受壓。

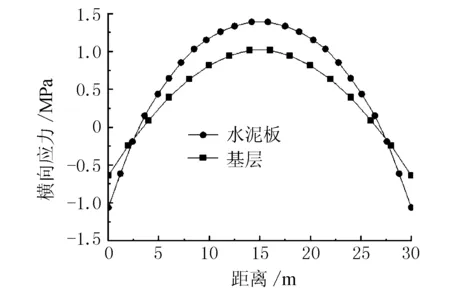
圖4 地基沉降30 mm/30 m作用下道面結構橫向應力

由圖4可見，在地基沉降最大值處，水泥板和基層的拉應力最大，且水泥板的拉應力大于基層的拉應力；在地基沉降開始和結束的位置處，水泥板和基層均出現了最大的壓應力，這是因為在該處出現了上拱翹曲變形。

地基差異沉降是否會引起水泥板開裂破壞是人們關注的主要問題，故本文主要分析地基差異沉降對水泥板應力的影響。不同跑道寬度和幅值條件下，在自重和飛機荷載作用下水泥板底部的最大拉應力見圖5。

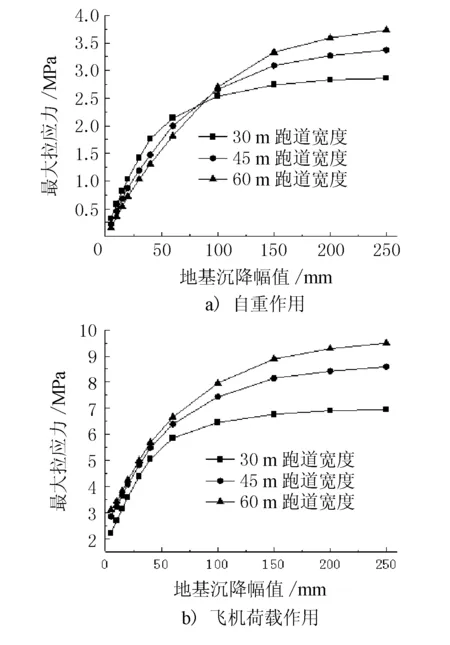
圖5 不同跑道寬度和幅值下水泥板底最大拉應力

由圖5a)可見，當跑道寬度一定時，在自重作用下水泥板底部最大拉應力隨著沉降幅值的增大而增大，應力增長呈現先陡后緩的趨勢。當地基沉降幅值一定時，隨著跑道寬度的增大，在自重作用下水泥板底部最大拉應力出現2種變化規律：當沉降幅值較小時，板底最大拉應力隨著跑道寬度的增大而減小；而當沉降幅值較大時，板底最大拉應力隨著跑道寬度的增大而增大。這主要是因為在沉降幅值較小時，水泥板能較好地跟隨變形，在相同沉降幅值下，較大的跑道寬度對應的沉降曲線更平緩，水泥板撓曲程度更小，板底最大拉應力也相對較小；而當沉降幅值較大時，水泥板與基層將出現分離，且隨著沉降幅值不斷增大，跑道寬度較大的水泥板底將出現更大的分離范圍，導致水泥板有更大范圍處于無支承狀態，板底最大拉應力也相應更大。

對比圖5b)可見，在相同沉降條件下，與自重作用相比，飛機荷載作用下的水泥板底最大拉應力有明顯增加，增加量為2.0～5.7 MPa。當跑道寬度一定時，飛機荷載作用下水泥板底最大拉應力隨沉降幅值的增大而增大，應力增長同樣呈現先陡后緩的趨勢。當地基沉降幅值一定時，隨著跑道寬度增大，飛機荷載作用下的水泥板底最大拉應力也隨之增大。這與自重作用下所呈現的規律有所不同。這主要是因為在模擬飛機荷載作用時，不同的跑道寬度采用了不同的飛機荷載，其中A380-800所引起的板底應力較大，B777-300次之，B737-700最小，導致在相同沉降幅值下，板底最大拉應力出現隨跑道寬度增大而增大的現象。

4 地基橫向差異沉降控制標準分析

從前文分析可知，地基橫向差異沉降會引起道面結構變形和附加應力，嚴重時會影響道面的橫向排水性能，并導致道面結構開裂或破損，故本文從水泥板開裂和道面排水性能兩方面分析地基橫向差異沉降控制標準。

將水泥板彎拉應力作為控制道面結構開裂的條件，若水泥板底的最大拉應力大于設計彎拉強度，水泥板將出現開裂破壞。該機場跑道水泥混凝土設計彎拉強度均為5.0 MPa。本文利用飛機荷載作用下水泥板底部最大拉應力的計算結果，通過線性插值得到不同跑道寬度下，當板底最大應力超過設計彎拉強度時所對應的沉降幅值，即為沉降容許值。經計算，3C、4E、4F等級跑道所對應的橫向差異沉降容許值分別為39.2，32.6，30.5 mm，差異沉降率分別為0.26%，0.14%，0.1%。本文按此差異沉降容許值驗算道面的橫向排水性能。該機場跑道設計橫坡坡度均為1.5%。在發生此差異沉降后，3C、4E、4F等級跑道所對應的橫坡分別變為1.2%，1.4%，1.4%，均大于1%的最小橫坡要求，橫坡仍符合標準。

根據機場設計規范MH/T 5027-2013規定，對跑道縱向差異沉降應控制在0.1%～0.15%。從跑道橫向差異沉降上看，根據計算結果，控制其在0.1%～0.15%對道面結構和運營壽命也是合理的。對于3C跑道，橫向差異沉降的要求可適當放寬為0.26%。

5 結語

1) 地基橫斷面出現余弦型差異沉降時，道面各層結構沉降變形曲線接近余弦型曲線；隨著沉降幅值的增大，道面各層結構的最大變形量也隨之增大并逐漸趨于穩定，且水泥板與基層之間以及基層與地基之間將先后出現分離現象；跑道寬度越大，道面結構的沉降跟隨性越好。

2) 跑道寬度一定時，水泥板底部最大拉應力隨著沉降幅值的增大而增大并趨于穩定。而在自重作用下，當沉降幅值較小時，板底最大拉應力隨著跑道寬度的增大而減小；當沉降幅值較大時，板底最大拉應力隨著跑道寬度的增大而增大。

3) 不同等級的跑道所對應的橫向差異沉降容許值有所不同，對于寬度30 m的3C等級跑道、寬度45 m的4E等級跑道，以及寬度60 m的4F等級跑道，橫向差異沉降率應分別控制為0.26%，0.14%和0.1%。

由于差異沉降引起的附加應力較大，建議在道面結構設計中進行地基與道面的整體結構設計，并考慮差異沉降引起的附加應力。可根據地基的差異沉降水平及跑道等級，適當增加結構層厚度或材料抗拉強度以保證道面結構正常工作。