基于BAS算法的河渠突發水污染溯源

王忠慧，貢 力,2，康春濤，王 鴻，楊軼群

(1.蘭州交通大學土木工程學院，甘肅 蘭州 730070;2.蘭州交通大學調水工程及輸水安全研究所，甘肅 蘭州 730070)

突發水污染事件會使整個水生態環境遭到破壞，從而造成巨大的損失，甚至會引發社會動蕩，需采取必要的應急措施來應對[1-2]。在水污染事件發生的第一時間判斷出污染源的位置、掌握其污染物的源強、獲知污染事件發生的時間[3]，是處理這種不確定性問題的關鍵所在，而能否快速有效地找到污染源的位置決定著能否最大限度減小突發水污染事件影響的范圍[4]。

突發水污染事情追蹤溯源就是了解水污染發生以及發展的全過程，而源項信息的識別尤其關鍵，國內外在源項信息識別方面已取得了很多研究成果，但還沒有形成一個完整的解決突發水污染事情溯源問題的體系。源項信息識別常用的方法有確定性方法、概率統計方法和耦合的概率密度分析方法3類[5]。在確定性方法研究方面，辛小康等[6]通過遺傳算法與數學模型相結合的方法，對一維單點源單變量和多點源多變量問題分別進行了研究；Boano等[7]利用地質統計法有效恢復了任意分布源和多個獨立點源的水污染釋放歷史；曹宏桂等[8]將水污染問題利用有限元法進行正演，用PSO-DE混合優化算法結合移動監測平臺進行反演，證明了該優化算法在二維水環境下的適用性。確定性方法最大的特點是利用一組最優的污染物濃度信息求解污染源項；缺點是計算量較大且沒有充分考慮數據的不確定性，而且當信息不準確時往往結果誤差很大。在概率統計方法研究方面，陳海洋等[9]在考慮有限寬度河流瞬時岸邊污染泄漏的情況下，建立了水體污染識別數學模型，并以典型Metropolis算法構建馬爾科夫鏈取得后驗概率分布；姜繼平等[10]通過Adaptive Metropolis算法對后驗概率密度進行采樣，得到了操作參數推薦值，為貝葉斯推理技術的應用作出了重要貢獻；Wei等[11]通過分析正向模型的不確定性，結合AM算法對假想的河道排放污染物源項進行了反演。概率統計方法的應用主要是考慮到了突發水污染事件的不確定性，雖然能得到污染源項的“可能解”，但是計算時抽樣過程極為耗時且結果對隨機變量的分布信息過于依賴。在耦合的概率密度分析方法研究方面，早期的逆向概率密度函數來自地下水污染的研究，Neupauer等[12]研究表明，在一維和二維環境下的地下水，可以用逆向概率密度函數求得源項的位置和時間信息；程偉平等[13]將水污染釋放過程重構，通過對比傳統的優化方法與逆向概率密度的優化方法，結果表明逆向概率密度優化方法減少了計算量，提高了計算效率；王家彪等[14]提出結合概率密度分析的微分進化法對突發水污染事情進行溯源研究。耦合的概率密度分析方法通過實現源項信息之間的解耦，確保在計算過程中計算量不會過大，也能考慮到突發水污染事件的不確定性，是確定性方法和概率方法的結合。耦合的概率密度分析方法不僅簡化了水污染溯源的過程，而且提高了溯源精度，是新一代的溯源研究方法。

本文采用耦合的概率密度分析方法，將突發水污染溯源的模型簡化，利用天牛須搜索(beetle antennae search，BAS)算法[14]識別一維河渠污染物源項，并通過Matlab進行模型仿真試驗來驗證BAS算法的可行性及應用前景。

1 數學模型

水污染溯源問題就是通過已檢測到的固定時刻的質量濃度信息確定污染源位置x、排放時刻t及源強m03個污染物源項[15]。本文通過水力學計算方法，利用正向質量濃度概率密度函數(污染物從污染源傳播到下游某一斷面的概率)與逆向位置概率密度函數(從觀測者角度出發，由觀測斷面判斷污染物可能來自任意位置的概率)之間的關系，實現源項3個未知量之間的解耦，進而通過質量濃度與位置概率密度函數之間的相關關系以及質量濃度與正向質量濃度概率密度函數之間的關系，構建水力學模型。

假設河渠在長度方向上遠遠大于寬度和深度方向，則污染物排入水體后能在短時間內與水體混合均勻，并且水流流速與污染物質量濃度均勻分布。在污染物只隨流程方向變化的情況下，污染物輸移數學模型可以簡化為一維的水流水質耦合模型[16]，計算公式為

(1)

式中：ρ(x,t)為污染物在x斷面t時刻的平均質量濃度，mg/L；u為河渠斷面平均流速，m/s；E為渠道縱向離散系數，m2/s；K為污染物降解系數，s-1。

若水污染的排放形式為瞬時排放，則污染源以下河渠中的污染物質量濃度隨河長的變化規律為

ρ(x,t)=

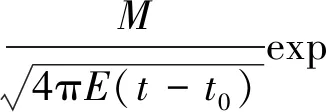
(2)

式中：M為瞬時排放的污染物面源強度，即源強，g/m2；x0為污染物排放位置，m；t0為污染物排放時間，s。

任何形式的水污染在河渠輸移過程中都可以用兩種概率密度函數來表示：一種表示污染物在河渠中的質量濃度分布，為正向質量濃度概率密度函數，即污染物從源頭傳播到下游某一位置的質量濃度分布概率；另一種表示從觀測斷面判斷污染物可能在上游的某個斷面，為逆向位置概率密度函數，反映污染物在不同位置的可能性大小。而耦合的概率密度分析方法就是通過對比發現正向質量濃度概率密度函數與逆向位置概率密度函數之間的關系，實現污染物排放位置、時間和源強之間的解耦。

該方法起初用于對地下水的研究，Neupauer等[17]得到了一維地下水域條件下正向質量濃度概率密度與逆向位置概率密度之間的關系：

(3)

式中：P為t′時刻從斷面x2推斷污染物的源頭位置x1處的逆向位置概率密度，具有m-1的量綱；t′為逆向計算時間點；P′為t時刻污染物由x1斷面輸移到x2斷面的正向質量濃度概率密度，也具有m-1的量綱。

因為P與P′具有相同的量綱，分別表示逆向位置概率密度輸送過程與正向質量濃度概率密度輸送過程，兩者之間是相互伴隨的過程，所以兩者之間具有高度的耦合性，即下游給定斷面觀測到的質量濃度過程與污染源在某一時刻出現在某一位置的概率相對應。

由式(2)(3)可推導得出逆向的位置概率密度為

P(x1,x2,t′)=

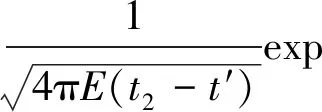
(4)

式中t2-t′為污染物從x1斷面(源頭位置)到x2斷面所用的時間。

由式(4)可知在污染源位置和釋放時間信息已知的情況下，就可以計算得到逆向位置概率密度P。

2 優化模型

2.1 優化模型的構建

由式(3)可知，逆向位置概率密度P與觀測的質量濃度系列ρ之間線性相關，其相關系數r=1。相關系數的表達式為

(5)

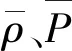
優化模型建立的目的就是尋找最優解，既然逆向位置概率密度函數已經實現了污染源排放位置、時間和源強之間的解耦，便可以先從水污染現場推測得到的一系列污染物排放位置、時間，即x′0、t′0中尋優，確定最優的x′0、t′0為x0和t0，再計算得到M。

根據觀測的質量濃度系列ρi，假定的x′0、t′0以及對應時刻的質量濃度信息得到Pi的表達式，構造目標函數如式(6)所示。對于目標函數式(6)，當且僅當x′0=x0、t′0=t0時，相關系數r=1，此時目標函數達到最優狀態。

min(1-r)

(6)

由式(6)得到污染物排放位置和時間，則源強M可由下式大致推算：

(7)

然后利用正向質量濃度概率密度函數與質量濃度信息之間的關系，進一步構建優化模型計算最終源強，其目標函數為

(8)

2.2 優化模型的求解

本文使用BAS算法求解一維河渠穩態點源擴散模型，該算法是2017年提出的一種高效的智能優化算法[18]，它通過模擬天牛搜索食物的過程進行優化計算。天牛是甲蟲一族，它最大的特征是擁有兩只比身體還要長的觸角(須)，當天牛覓食的時候，利用兩須搜索食物氣味，通過食物的氣味(也就是目標函數)控制移動行為和轉向行為來搜索食物，當天牛搜索到食物的時候也就是計算得到最終的優化結果的時候。為了使模型的計算結果精確，本文將BAS算法中的步長進行改進，采用變步長的BAS算法求解模型，隨著步長的減小，算法的計算速度由快變慢，完成從全局到局部尋優的一個過程，可以有效縮短算法的收斂速度，提高算法的計算精度。具體計算步驟如下：

步驟1：確定優化模型的目標函數(式(6)(8))。

步驟2：以al表示左須位置，ar表示右須位置，o表示質心，用d0表示兩須之間的距離。假設天牛頭朝向任意，因而從天牛右須指向左須的向量朝向也是任意的，由歸一化的隨機向量l表示：

(9)

式中:rands(m,1)為一隨機向量，與天牛須的指向有關；m為維數，即目標函數未知數的個數。

步驟3：經過G次迭代后，天牛左右兩須的位置可以根據l確定為

(10)

式中：aG為第G次迭代后質心的位置；dG為第G次迭代時天牛兩須的距離。

步驟4：由左右兩須的適應值確定天牛下一時刻的位置坐標；

aG=aG-1+slsign[f(al)-f(ar)]

(11)

其中

s=cd0

式中：s為步長；c為常數；f(al)為al的適應度值，表示向左走；f(ar)為ar的適應度值，表示向右走；sign為符號函數，若f(al)f(ar)，此時天牛向右須方向移動。每進行一次迭代，搜索距離和步長的變化如下：

dG=η1dG-1+d0

(12)

sG=η2sG-1

(13)

式中η1、η2分別是搜索距離更新系數與步長衰減系數。

步驟5：將步驟4計算得到的aG代入目標函數式中，直到找到目標函數的最優解或達到最大迭代次數，結束迭代。

BAS算法流程如圖1所示。

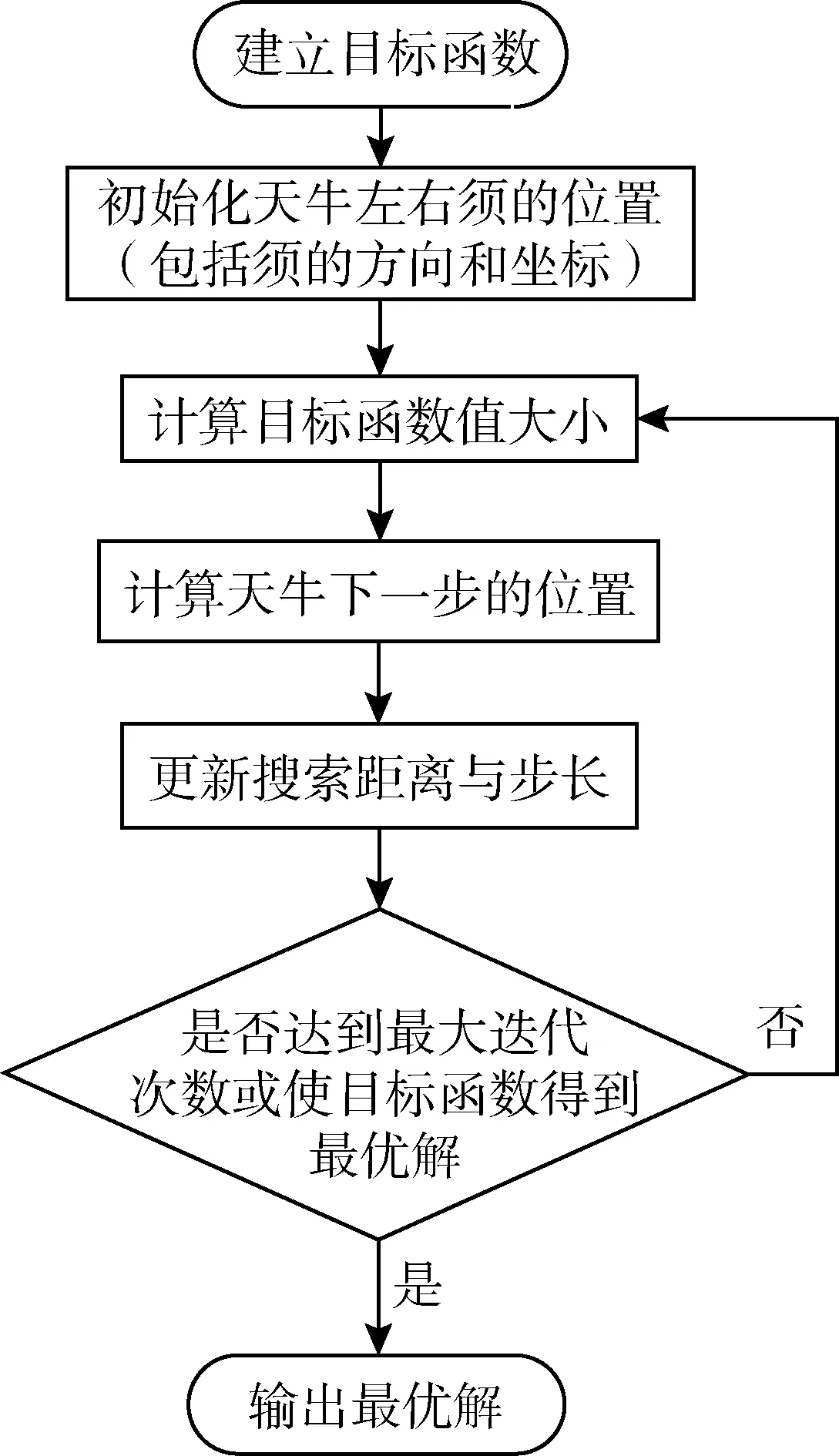
圖1 BAS算法流程Fig.1 BAS algorithm flow chart

3 模型仿真試驗

綜合考慮了南水北調中線[19]、引大入秦輸水渠道等一些實際河渠的基本輸水狀況后，選定一段沒有支流匯入或突然涌泄水的、可視為一維恒定流進行計算的矩形斷面的河渠進行仿真試驗。河渠為漿砌塊石護面，糙率系數為0.025，底寬為10 m，水深 4 m，坡降0.002 8%，流速0.36 m/s，河渠縱向離散系數為2.0 m2/s。假設上午9:00在A斷面處(假定此處為坐標原點)瞬時排入1 000 kg的污染物，為了便于對比分析污染物的質量濃度變化過程以及驗證BAS算法的計算結果，在下游河道設置了距A點800 m和1 200 m的A1和A2兩個監測斷面。根據污染物擴散模型(式(2))，在不考慮降解作用的情況下，分別計算兩個斷面的質量濃度過程，并在得到的計算結果中人為加入10%的觀測誤差(也就是在污染物擴散模型中得到的質量濃度數據中加入10%以內的變幅)，生成污染物質量濃度變化過程如表1所示。

為便于說明BAS算法計算本文優化模型的可行性，將得到的兩斷面質量濃度信息分別進行兩次水污染溯源計算。選擇Matlab軟件進行模型仿真計算，取初始步長為1 000，迭代200次，再進行50次計算求取平均值后，得到計算結果如表2 所示。

從表2可看出，由A1斷面計算得到的污染物質量為975.72 kg，與實際值相比誤差為2.43%，計算得到的排放位置差25.43 m，排放時間超出7 min；由A2斷面計算得到的污染物質量為964.32 kg，與實際值的誤差為3.57%，計算得到的排放位置差56.22 m，排放時間超出9 min。通過不同觀測斷面的兩次計算結果發現，由A1斷面的濃度信息計算得到的源項信息的精度比A2斷面高。因為在計算過程中沒有考慮降解作用，所以不能從水力學的角度來分析誤差。考慮到BAS算法在計算時對初始步長的選取具有一定的隨機性,并且通過多次計算發現當初始步長在大于自變量2/3的范圍內取值時，計算結果的精度較高。由于兩個斷面所求的污染物排放位置和時間(即自變量)范圍不同，A2斷面的自變量范圍較A1斷面大，因此，初始步長為 1 000時，對于A2斷面來說，得到的溯源精度就沒有A1斷面高。在實際發生突發水污染事情時，可以通過現場考察或是通過已有的資料分析得到自變量的大致范圍，再計算源項，便可得到更加精準的污染物排放位置和時間。

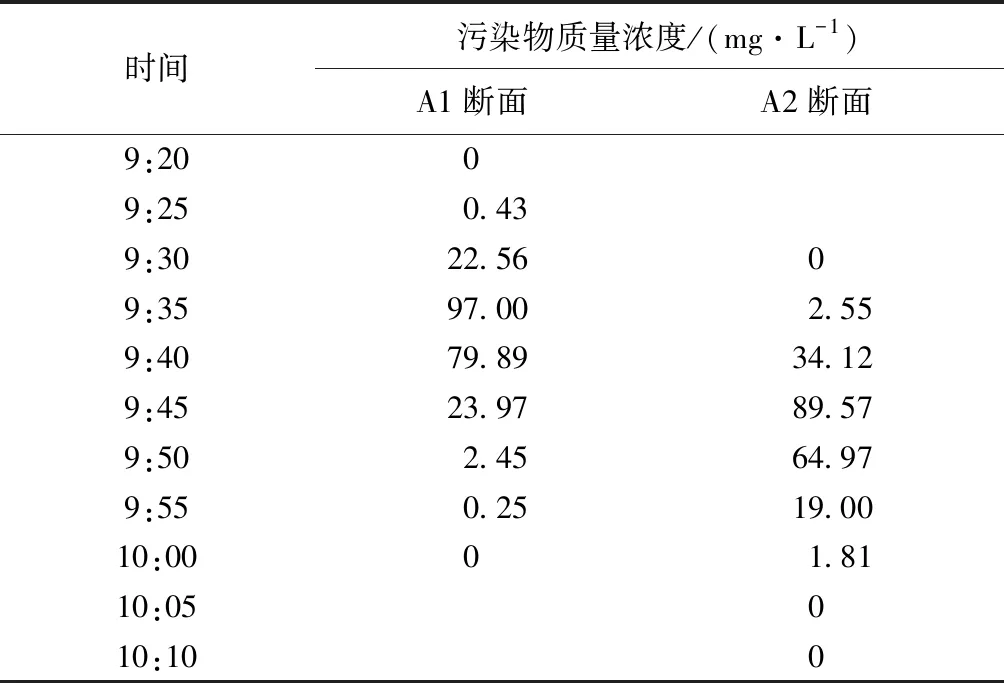
表1 人工生成的觀測斷面污染物質量濃度Table 1 Mass concentration information in observed section

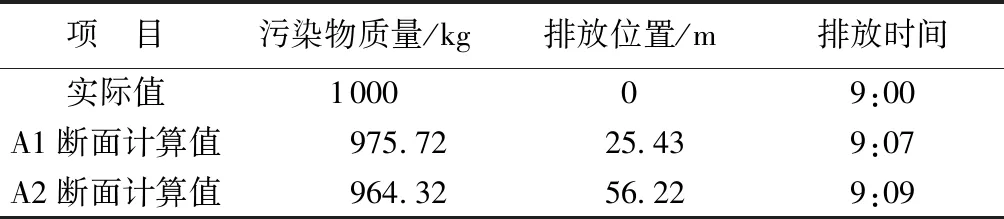
表2 仿真溯源結果Table 2 Table of simulation traceability results

為了測試溯源結果的準確性，把由A1斷面計算得到的源項信息代入污染物擴散模型(式(2))中，得到污染物在A1斷面處的計算質量濃度變化過程；將計算質量濃度變化過程與觀測質量濃度變化過程進行比較(圖2)可知，在質量濃度未達到峰值之前計算質量濃度較觀測質量濃度高，但質量濃度達到峰值之后，觀測質量濃度系列比計算質量濃度系列大。總體上，兩條曲線的相關性較高，溯源的計算結果具有較高的精度，因此溯源模型重構的突發水污染事件能夠反映實際水污染全過程。

為說明BAS算法在突發水污染溯源計算中的特點，在模型仿真試驗中采用粒子群算法(partical swarm optimization，PSO)進行了計算，結果表明，同樣取50次計算結果的平均值，PSO算法的精度比BAS算法高。但進一步分析發現BAS算法在迭代了106次之后趨于穩定，而PSO算法迭代了564次后才趨于穩定；BAS算法計算50次后取平均值的計算精度與PSO算法計算42次后取平均值的計算精度相同，但BAS算法所用的總計算時間為30 s，而PSO算法為125 s。可見BAS算法的單次計算精度比PSO算法低，但是BAS算法收斂速度快，達到相同的計算精度BAS算法所用的計算時長也明顯低于PSO算法。

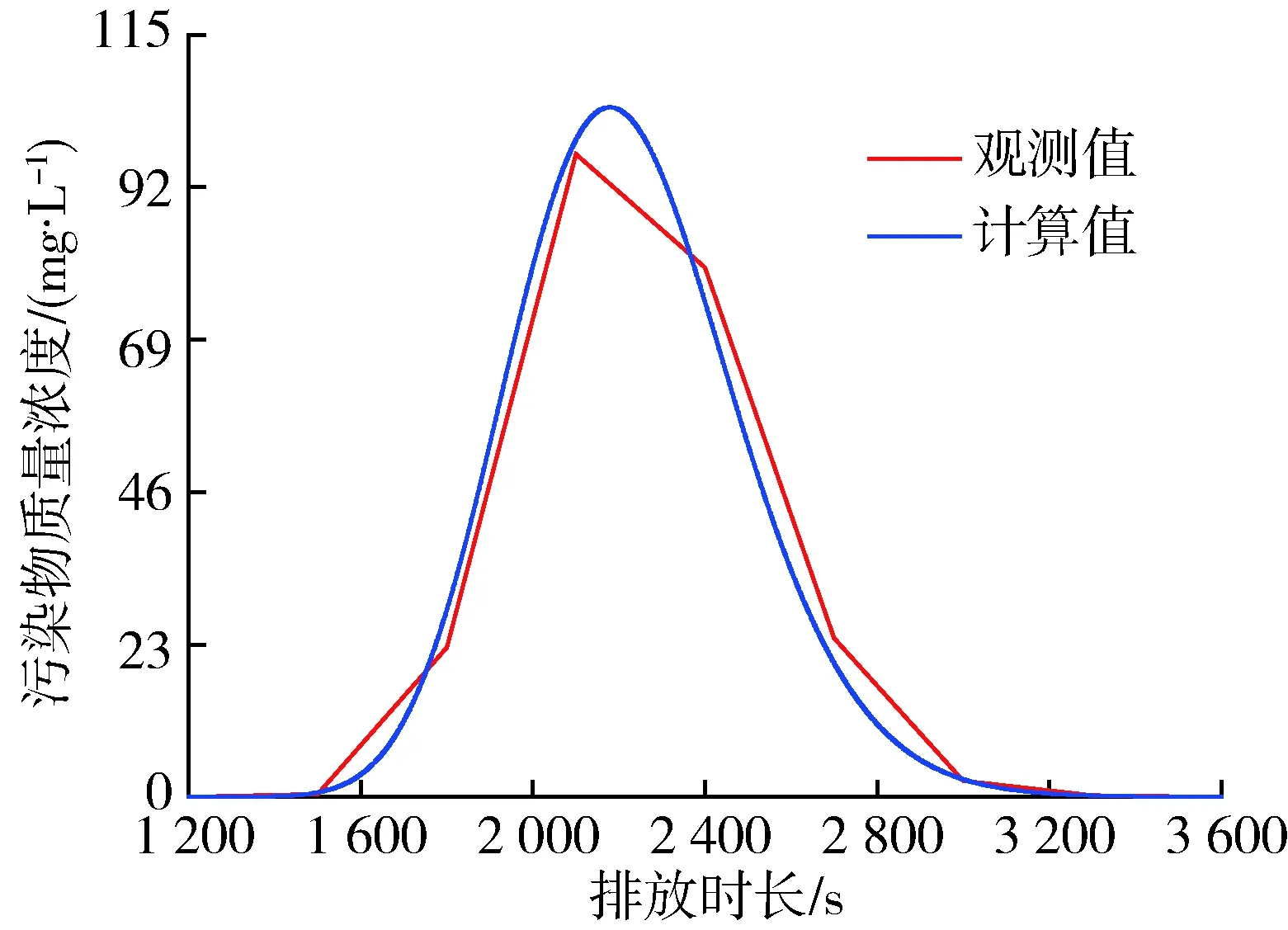
圖2 A1斷面污物物質量濃度過程Fig.2 Concentration process diagram of A1 section

總體來說，BAS算法計算結果精度高，收斂速度快，算法簡單，在將來的基于污染物源項解耦的突發水污染溯源方面有較好的應用前景。但BAS算法在計算過程中步長一直在隨著迭代次數的增加而減小，無論能否進一步找到最優位置，步長一直在衰減，缺少一種反饋機制，這也是BAS算法在水污染溯源研究中有待提高的地方。

4 結 語

本文利用耦合的概率密度分析方法將一維水力學條件下的正向的質量濃度信息與逆向的位置信息進行解耦，構建了污染物排放時間、位置和源強解耦后的水力學模型。將優化后的水力學模型利用BAS算法進行模型仿真計算，發現BAS算法可以很好地實現源項信息的求解；通過不同斷面的溯源計算以及與PSO算法進行比較，結果表明BAS算法收斂速度快，運算量小，但是步長具有衰減性，不管每一步計算得到的結果是否變得更優，步長總會衰減，但多次求取平均值后可以達到計算精度要求。本文論證了BAS算法在突發水污染溯源領域的可行性，拓寬了BAS算法的應用領域，但是對于復雜的水力學模型以及更高維問題的研究還有待深入。