基于控制流的軟件設計與實現一致性分析方法

張家奇，牟永敏，張志華

（網絡文化與數字傳播北京市重點實驗室（北京信息科技大學），北京 100101）

（*通信作者電子郵箱879632300@qq.com）

0 引言

近年來，隨著軟件產業化的發展，軟件測試逐漸成為人們關注的焦點。軟件測試的目的在于檢驗某個軟件系統是否滿足規定的要求，即驗證軟件設計與實現是否一致。對于小規模的軟件系統，人工可以完成一致性的驗證。對于軟件規模和復雜度較高的軟件系統，人工難以完成一致性的驗證。自動完成軟件設計與實現的一致性驗證工作變得越來越重要。

軟件實現與設計一致性驗證是指對已完成的軟件系統，驗證其功能實現是否按照軟件設計說明書的要求完成，是一種非常重要的測試［1］。Riedl-Ehrenleitner 等［2］提出面向設計模型和代碼的一致性檢測方法，通過一致性規則實時驗證代碼和設計模型的一致性，用于模型驅動的軟件開發，并在開發過程中實時檢測代碼與設計模型的一致性，沒有考慮代碼的編寫細節。曾一等［3-4］提出基于統一建模語言（Unified Modeling Language，UML）模型與Java 代碼一致性檢測的方法，對設計和實現的動態交互信息進行一致性驗證，但沒有對具體方法的實現進行驗證。牟永敏等［1］提出一種針對文檔和源代碼的測試方法，該方法基于函數調用路徑［5］，從設計文檔中獲取函數的功能描述，建立設計功能簇模型；從源代碼中提取實現函數特征，對比已知的模板集獲取實現函數的功能描述，建立系統功能簇模型；通過驗證兩個模型的一致性完成設計與實現一致性驗證問題。但是該方法需人工分析設計文檔以及大量的模板集，限制了模型建立的效率，并且該方法沒有對比設計函數的實現細節與實際函數的實現細節是否一致。

本文參考文獻［1］中提出的一致性驗證方法，提出了一種面向偽代碼的函數特征提取方法，選取設計文檔中的偽代碼和程序源代碼為研究對象，通過驗證偽代碼和源代碼中函數特征的一致性完成設計與實現的一致性檢測。此處申明本文研究的前提為設計文檔中包含偽代碼，且偽代碼語義正確。

1 本文方法

本文研究思路基于軟件設計的模塊化設計原理。模塊化原理就是把程序劃分成若干個模塊，每個模塊完成以一個子功能，把這些模塊集中起來組成一個整體，可以完成指定的功能，滿足問題的需求［6］。模塊化原理不僅使軟件結構清晰，而且讓軟件容易測試和調試。

軟件設計過程中遵循模塊化原理。同樣，設計文檔也遵循模塊化原理，詳細描述各個模塊的實現算法、邏輯流程等。從文檔對各模塊的偽代碼描述和程序源代碼的各模塊中提取函數特征，并建立設計特征模型和軟件實現特征模型，通過計算模型的相似度解決設計與實現的一致性驗證問題。本文一致性檢測框架如圖1所示。

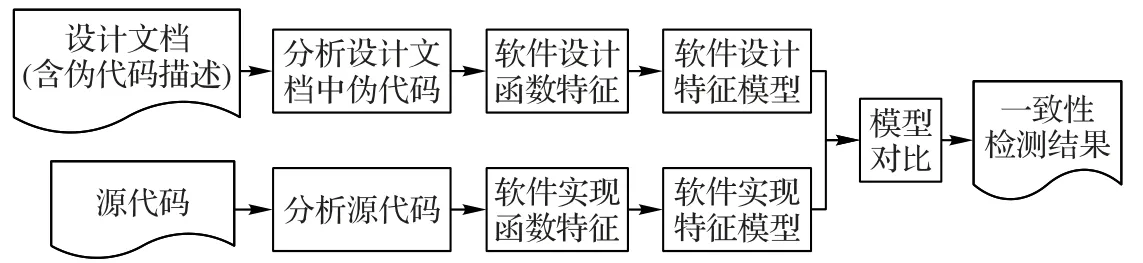
圖1 一致性檢測框架Fig.1 Framework of consistency detection

2 函數特征的提取

在軟件實現和設計一致性檢測中，偽代碼和源代碼的表征方式決定了軟件設計信息和實現信息的利用程度。在代碼克隆領域，代碼的表征方式分為文本［7］、詞匯［8］、語法［9］和語義［10-11］四個層次［12］。由于偽代碼變量不需要聲明、缺乏語法規范的特點，文本、詞匯的表征方式不能充分利用偽代碼的信息。語法的表征方式，例如基于語法分析樹的方式，會造成一致性驗證算法復雜度的提升。語義的表征方式，利用代碼語義信息進行驗證，其中，語義信息是指能夠反映一段代碼功能的信息，比如代碼的控制流和數據流［12］971。本文采用基于語義的表征方式，語義信息為代碼的控制流，基于代碼控制流獲取函數特征。

函數特征分為外部特征和內部特征。外部特征為函數間調用關系，內部特征為函數控制流信息，包括基本塊序列和控制流圖。函數間調用關系反映了系統的結構［13］，每個函數內部的控制流信息反映了函數的內部結構，因此選其作為函數特征并建立特征模型。函數特征提取具體過程如下：

2.1 中間表示的生成

偽代碼和源代碼中的控制結構會造成控制流的改變，難以直接從中獲取控制流信息，因此將其轉換成一種按順序執行的語句序列——中間表示。該過程包括偽代碼中間表示的生成和源代碼中間表示的生成。

2.1.1 偽代碼中間表示的生成

偽代碼中間表示（Pseudocode Intermediate Representation，PIR）是一種按順序執行的語句序列。常見的中間表示有很多形式，如三元式、四元式、后綴式、語法樹等［14］，本文采用三元式。在生成PIR 過程中，首先對偽代碼進行語法規范，根據語法規范對偽代碼進行詞法和語法分析，生成語法分析樹；然后遍歷語法分析樹，根據語法制導翻譯將其中的控制結構轉換為順序執行的語句和跳轉語句——中間代碼；最后對中間代碼劃分基本塊，得到中間表示。

1）偽代碼語法規范。

由于人們在描述算法時使用的偽碼并不相同［6］128，難以一般化，本文使用一種較為通用語法規則來規范偽代碼。語法規則用擴展巴科斯范式表示，語法規則產生式如下：

其中：每一個分號語句為一條規則，大寫字母開頭為詞法規則，小寫字母開頭為語法規則。NL 表示換行符，語法規則中的單引號內容和大寫單詞表示匹配對應的字符；prog 表示偽代碼的一個邏輯結構，包括一個或多個函數定義；functiondef 為函數定義，包括語句集stats；id 表示標識符；number 表示數字。為方便后文引用，語法規則結尾添加編號。

語句集stats 包含if語句、if_else 語句、while 語句、repeat語句、for語句、賦值語句、函數調用語句等。expr為表達式，包含邏輯表達式、關系表達式、算數表達式等。

2）生成語法分析樹。

使用ANTLR（ANother Tool for Language Recognition）生成語法分析樹和樹遍歷器。ANTLR 是一款強大的語法分析器生成工具，可以根據語言的語法生成一個語法分析器和語法分析樹遍歷器，并自動建立語法分析樹。

3）語法制導翻譯。

語法制導翻譯是在語法分析過程中，根據每個產生式所對應的語義子程序進行翻譯的方法［14］22。通過語法制導翻譯可以將偽代碼語句翻譯為按順序執行的語句。使用ANTLR內置的樹遍歷器遍歷語法分析樹，樹遍歷器采用遞歸下降的分析方法遍歷語法分析樹，在遍歷的過程中使用語法制導翻譯，生成按順序執行的中間代碼。

偽代碼中函數定義語句、函數調用語句、賦值語句、關系表達式并不影響模塊的控制流，這些語句的產生式對應語法規則（1）、（7）、（8）、（11），其語義子程序（翻譯規則）不需要對原語句進行處理，即在中間表示中復用原語句。

偽代碼中布爾表達式經常用來改變控制流和計算邏輯值，但其使用意圖要根據其語法上下文來確定，例如關鍵字IF后面的布爾表達式用來改變控制流，而一個賦值語句右部的布爾表達式用來表示一個邏輯值。因此將控制語句（IF-ELSE、WHILE 語句等）以及布爾表達式結合進行語法制導翻譯，再將翻譯的結果填寫在中間表示中。

布爾表達式是布爾運算符作用于布爾變量或關系表達式上而構成的［14］315，控制結構是布爾表達式作用于控制語句而構成的。布爾表達式生成文法的產生式對應語法規則（8）～（10）。控制結構生成文法的產生式對應語法規則（2）～（6）。由于篇幅限制，只列出一種while 循環語句，for 和repeat 循環語句語義子程序與while循環語句類似。

由于邏輯運算短路的特點，偽代碼中會出現短路代碼，進而影響程序控制流。因此將運算符and、or、not 翻譯成goto 語句。運算符本身不出現在中間表示中，布爾表達式的值通過語句序列中的位置來表示。如表1 所示，使用轉移語句來翻譯控制語句以及布爾表達式。

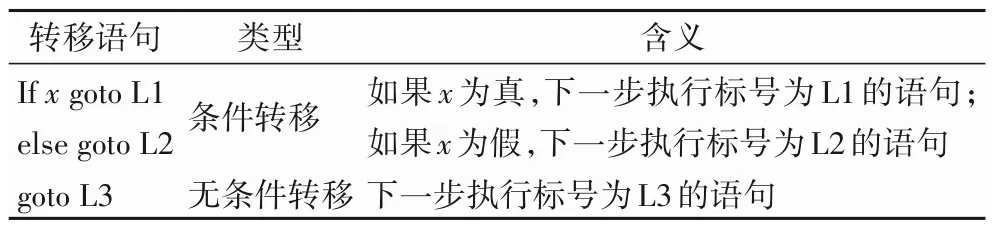
表1 轉移語句Tab.1 Transfer statements

PIR 中的語句將按順序執行，當遇到以上語句時，執行過程就會跳轉。在一個語句前加上前綴“Li：”，表示將標號Li附加到該語句，其中i為正整數。同一個語句可以同時擁有多個標號。

為方便描述，需賦予文法符號（非終結符）屬性：text、code、begin、next、true、false。其中，text 表示語句或表達式未經處理的token 流，code 表示語句翻譯后的代碼，begin、next、ture、false 表示標號。如stat.code 表示語句stat 翻譯后的代碼；stat.begin 表示語句stat 的標號；stat.next 表示語句stat 后一條語句的標號；expr.true 表示布爾表達式expr 為真時跳轉到目標語句的標號。后文圖中“=”表示賦值，newlabel 表示產生一個新的前綴標號“Li”；gen（）表示一個語句，如：假設expr.true 的值為“L1”，則gen（“goto”expr.true），表示語句“goto L1”。

由于關系表達式、函數定義語句、函數調用語句、賦值語句對應生成文法的語法制導規則不需要對原語句進行特殊處理，因此本文只列出語法規則（1）所對應語法制導規則。如圖2（a）所示。

圖2 語法制導定義Fig.2 Syntax-directed definitions

布爾表達式的語法制導翻譯規則與編譯原理［14］317中布爾表達式制導翻譯規則類似，不做詳細描述。圖2（b）～（d）分別列出了語法規則（2）、（3）、（5）對應的語法制導翻譯規則。根據圖2 語法制導翻譯規則，可將偽代碼翻譯為中間代碼，如圖3（a）中偽代碼翻譯為圖3（b）中的中間代碼。

4）中間代碼優化和基本塊的劃分。

如圖3（b）中語句L7，語法制導翻譯生成的中間代碼存在空語句，需對中間代碼進行優化。使用ANTLR 生成中間代碼對應的語法分析樹，遍歷語法分析樹并使用算法1 對其優化，優化結果如圖3（c）。

算法1 中間代碼優化算法。

為了更好地分析控制流，將中間代碼劃分為基本塊。基本塊是滿足下列條件的最大的連續中間表示語句序列［15］：

a）控制流只能從基本塊的第一個語句進入該塊。即沒有跳轉到基本塊中間的轉移指令。

b）除了基本塊的最后一個語句，控制流在離開基本塊之前不會停止或跳轉。

因此，每一個基本塊對應一個入口語句，只需確定入口語句即可劃分基本塊，選擇入口語句規則如下：

a）中間代碼的第一個語句；

b）能由轉移語句轉移到的語句；

c）緊跟在一個轉移語句之后的語句。

每個入口語句對應的基本塊包括了從它自己開始，直到下一個入口語句或結尾語句之間的所有語句。如圖4 所示，對圖3（c）中優化結果的基本塊劃分，其中bb代表基本塊。

圖3 偽代碼翻譯及優化結果Fig.3 Pseudocode translation and optimization results

圖4 基本塊劃分結果Fig.4 Result of basic block partitioning

2.1.2 源代碼中間表示的生成

GNU 編譯器套件（GNU Compiler Collection，GCC）可將源代碼轉換為中間表示。通過GCC 調試選項-fdump-tree-cfg 并輸入源代碼，即可得到GCC編譯器生成的cfg中間文件。文獻［1］中使用該方法提取源代碼函數結構特征。cfg 文件中的中間代碼是GCC 編譯器對源代碼進行詞法和語法分析后得到的中間表示，其中包含劃分基本塊后的結果以及基本塊的執行順序。如圖5（a）中源代碼以及通過GCC 編譯器生成圖5（b）中cfg中間碼。

2.2 函數特征提取

相關定義如下：

定義1函數調用關系圖可以表示為一種有向圖G=〈V，E〉。其中：V是節點集，每一個節點代表一個函數；E=｛（x，y）|x，y∈V｝是弧集，表示函數x調用了函數y。

定義2控制流圖是一種簡單的控制流表示方法，描述邏輯控制流。控制流圖G是一種有向圖G=〈B，D〉。其中：B為節點集合，每一個節點代表一條或多條語句，即一個基本塊；D=｛（x，y）|x，y∈N+｝是弧集，表示控制流向。

定義3基本塊序列（Basic Block Sequence，BBS）為一個有序序列bbs=b1，b2，…，bi，bj∈｛seq，con_jump，uncon_jump，seq_cj，seq_nj，return｝。其中：bj表示第j個基本塊；seq為只包含順序語句的基本塊；uncon_jump為只包含無條件轉移語句的基本塊；con_jump為只包含條件轉移語句的基本塊；seq_cj為包含順序語句和條件轉移語句的基本塊；seq_nj表示包含順序語句和無條件轉移語句的基本塊；return表示包含return 的基本塊。

1）函數調用關系的提取。

偽代碼函數調用關系的獲取。在遍歷語法分析樹的過程中，匹配functiondef 規則可獲取主調函數名稱及參數信息，匹配stat 規則中函數調用規則“id′（′args？′）′”可獲取被調函數名稱及參數信息。functiondef 規則結束則完成主調函數調用信息的提取，遍歷整個語法分析樹，即可獲取全部函數調用信息并生成函數調用關系圖。

源代碼函數調用關系的獲取。使用ANTLR，將cfg 文件輸入，生成語法分析樹。遍歷語法分析樹，匹配函數定義和函數調用語句，獲取函數調用關系。圖6 所示為源碼以及根據提取的函數調用關系生成的函數調用關系圖。

2）控制流信息的提取。

控制流信息包括函數內部的控制流圖和基本塊序列。在遍歷語法分析樹的過程中，根據基本塊中是否包含條件轉移語句、無條件轉移語句以及return 語句，判定基本塊，獲取基本塊序列。同時匹配轉移語句中的“goto bbi”，獲取基本塊流向，得到控制流圖。如圖5（c）中控制流圖，圖中節點為基本塊，其對應的基本塊序列bbs=uncon_jump，seq，con_jump，seq，return。

圖5 中間代碼和控制流Fig.5 Intermediate code and control flow

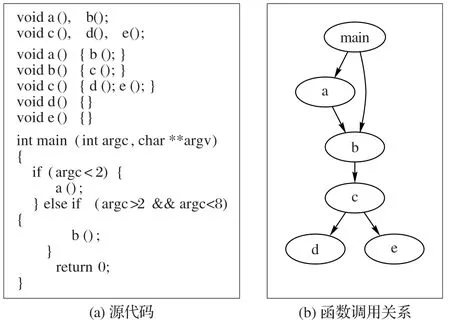
圖6 源代碼及其對應的函數調用關系Fig.6 Source code and corresponding function call relationship

3 特征模型的建立對比

3.1 特征模型的建立

設計文檔中的偽代碼描述了每一模塊的實現方式，包括實現算法、邏輯流程等，通過分析設計文檔中偽代碼，獲取設計函數間調用關系以及設計函數控制流，建立設計特征模型。通過靜態分析源代碼獲取實現函數調用關系以及每個函數的控制流，建立軟件實現特征模型。由于圖能有效表示對象的屬性以及對象之間的關系［16］，因此采用圖來表示函數調用關系和函數控制流信息。

根據函數特征中的函數間調用關系和函數控制流信息，分別建立函數調用關系圖和控制流圖。以函數調用關系圖為載體，將圖中每個節點映射到對應函數的基本塊序列和控制流圖，從而建立設計特征模型和軟件實現特征模型。

3.2 特征模型對比

對比軟件設計與實現的函數調用關系圖可以驗證實際系統是否按照設計要求的系統結構實現。對比軟件設計與實現函數的控制流圖可以檢查每個函數否是按指定的邏輯流程實現。因此，特征模型的對比包括函數調用關系圖和函數控制流圖的對比。

特征模型對比過程：首先進行外部特征（函數調用關系圖）的對比，通過計算函數調用關系圖的相似度來驗證外部特征的一致性。如果外部特征（函數調用關系圖）不一致，說明實際系統沒有按照設計要求的系統結構進行實現，直接給出系統結構不一致的檢測結果。如果外部特征（函數調用關系圖）一致，則獲取函數調用關系圖中函數的匹配狀態，并對匹配函數進行內部特征（控制流圖）的對比。通過計算控制流圖的相似度驗證內部特征的一致性，過程中可獲取獨立路徑的匹配狀況；然后逐一比對已匹配的獨立路徑，對路徑中每一個節點（基本塊）類型進行匹配，并標記類型不匹配的基本塊；最終獲取類型不匹配的基本塊標號，作為一致性檢測結果。

3.3 相似度的計算

定義4圖G使用二元組表示，即G=（V，E）。其中：V為圖G中的所有節點的集合；E?V×V表示邊的集合。

圖相似度的計算基于圖編輯距離，采用圖匹配算法領域中常用方法——二分圖編輯距離，將圖編輯距離問題轉化為二分圖匹配問題［17］。對源圖G1（V1，E1）和目標圖G2（V2，E2）構造完全二分圖G，圖G中邊的權值為圖中節點的相似度，節點相似度越大，權值越大。因此，圖G1、G2的相似度問題轉變為帶權二分圖最優匹配問題，采用Kuhn-Munkers 算法即可求出最大權匹配。Kuhn-Munkers 算法是一種二分圖最佳匹配算法，文獻［18-19］使用Kuhn-Munkers算法分析惡意代碼函數調用圖的相似度。

3.3.1 函數調用圖相似度計算

函數調用圖g1和g2所構成的二分圖G的邊權值通過對應函數的相似度和函數調用關系相似度聯合計算得到。下文中v1和v2分別表示圖g1和g2中的函數。

1）函數相似度計算。

函數v1和函數v2的相似度通過計算函數內基本塊序列bbs的相似度得到。代碼塊序列的相似度度量方法有多種，如最長公共子序列、后綴數組［20］、哈希比較法［21］、機器學習［22］等。在v1和v2的相似度度量中，bbs長度一致時，更能說明二者的相似性，即函數v1和v2對應的基本塊序列bbs1和bbs2長度是否相同，對應的權重是不同的。而最長公共子序列，后綴數組的方法，只能說明bbs1是否包含bbs2，精確度較低。哈希比較法又過于敏感，容易造成誤判。機器學習的方法需要大量的模板集，難以一般化。

本文采用萊溫斯坦距離（Levenshtein Distance，ld），萊溫斯坦距離是一種度量方法，通常用來比較基于字符序列的兩個字符串［23］。字符序列定義了字符串的結構［23］，基本塊序列類似于字符串序列，可以使用該方法計算其相似度。由定義3基本塊有6種類型，用1～6表示，則圖4中函數基本塊序列可表示為bbs=3，4，1，2，1，6。函數v1和v2的相似度計算公式如下：

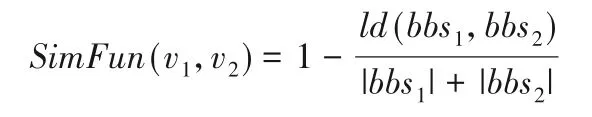
其中：bbs1、bbs2為函數v1、v2對應的基本塊序列；ld（bbs1，bbs2）為基本塊序列bbs1和bbs2的萊溫斯坦距離；|bbs1|、|bbs2|為兩個序列的基本塊個數。當基本塊序列得相似性達到一定的閾值，就認為兩個函數是相似的。大量實驗結果表明，基本塊序列的相似度達到80%，則可判定兩個函數是相似的。

2）函數調用關系相似度計算。

函數調用關系相似度計算公式如下：

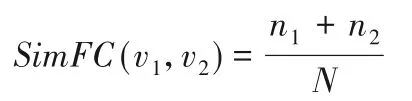
其中：n1為函數v1和v2的主調函數的相似對個數；n2為函數v1和v2的被調函數的相似對個數；N為函數v1、v2的主調函數和被調函數組成的所有函數對個數。

3）二分圖邊權值計算。

二分圖邊權值計算公式如下：

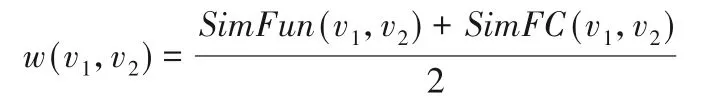
函數調用圖g1和g2對應的二分圖構造完成后，采用KM（Kuhn-Munkers）算法求其最大權匹配M，匹配M的邊權值占比為函數調用圖g1和g2的相似度，權值越大，相似度越大。圖相似度計算公式如下：

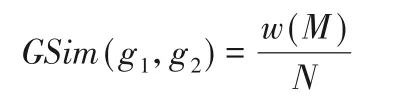
其中：w（M）為最大權匹配M的權值；N為圖g1和g2中函數構成的函數對個數。

3.3.2 控制流圖相似度計算

控制流cg1和cg2構成二分圖Gcg，二分圖Gcg的頂點為控制流圖cg1和cg2中的獨立路徑，圖Gcg的邊權值為圖cg1、cg2中各獨立路徑之間的相似度。

1）獨立路徑的相似度計算。

控制流圖中的獨立路徑為基本塊序列，相似度計算同樣采用萊溫斯坦距離。計算公式如下：

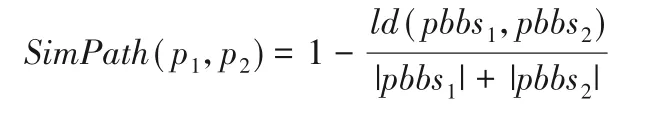
其中：pbbs1、pbbs2為獨立路徑p1與p2對應的基本塊序列；ld（pbbs1，pbbs2）為基本塊序列pbbs1與pbbs2的萊溫斯坦距離；|pbbs1|、|pbbs2|為兩個序列的基本塊個數。

2）控制流圖相似度計算。

采用KM 算法獲取二分圖Gcg的最大權匹配M，并根據匹配M計算控制流圖的相似度。計算公式如下：

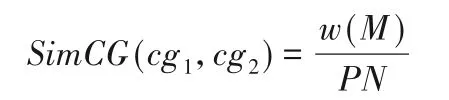
其中：w（M）為最大權匹配M的權值；PN為圖cg1和cg2中獨立路徑的對數。

4 實驗與分析

實驗采用數據結構中常規排序算法和查找算法，源代碼下載自GitHub（https：//github.com/TheAlgorithms/C）。偽代碼則根據各排序算法和查找算法的算法思路以及偽代碼語法規則人工編寫完成。由于函數間調用關系是否一致會導致實驗結果的不同，因此實驗一驗證不同函數調用關系情況下的一致性檢測結果。由于本文一致性檢測方法依賴于設計文檔偽代碼，因此實驗二驗證在設計文檔偽代碼功能描述不完善情況下的一致性檢測結果。使用本文方法，分析功能完全的設計文檔偽代碼獲取函數特征并建立設計特征模型。如圖7所示。

圖7 設計特征模型Fig.7 Design feature model

4.1 實驗一

軟件設計與軟件實現之間可能存在以下幾種情況：

1）實現系統完全按照設計要求實現了所有函數，實現系統函數調用關系滿足設計要求，需要進行函數調用關系圖和控制路圖的對比，如實驗Code1。

2）實現系統按照設計要求實現了所有函數，但存在部分函數調用關系與設計要求不一致，如實驗Code2中函數Search和Sort未調用任何函數。

3）實現系統實現系統未實現所有函數，但其函數調用關系與設計要求部分一致，如實驗Code3只實現了排序功能。

分析被測代碼，獲取實際函數特征模型，與設計特征模型進行對比。表2 顯示了實現與設計系統中各函數匹配結果以及函數調用關系相似度simFC。simFC＞0.8表示匹配成功，且函數基本塊序列和函數調用關系非常相似；0＜simFC＜0.8 表示匹配到函數但函數基本塊序列或者函數間調用關系一致度較低；simFC=0表示未匹配到對應函數。Code1為與設計特征模型中函數調用關系一致的代碼；Code2 為與設計特征模型中函數調用關系部分一致的代碼，其中函數Sort 和Search 未調用任何函數；Code3為只實現了查找功能的代碼。

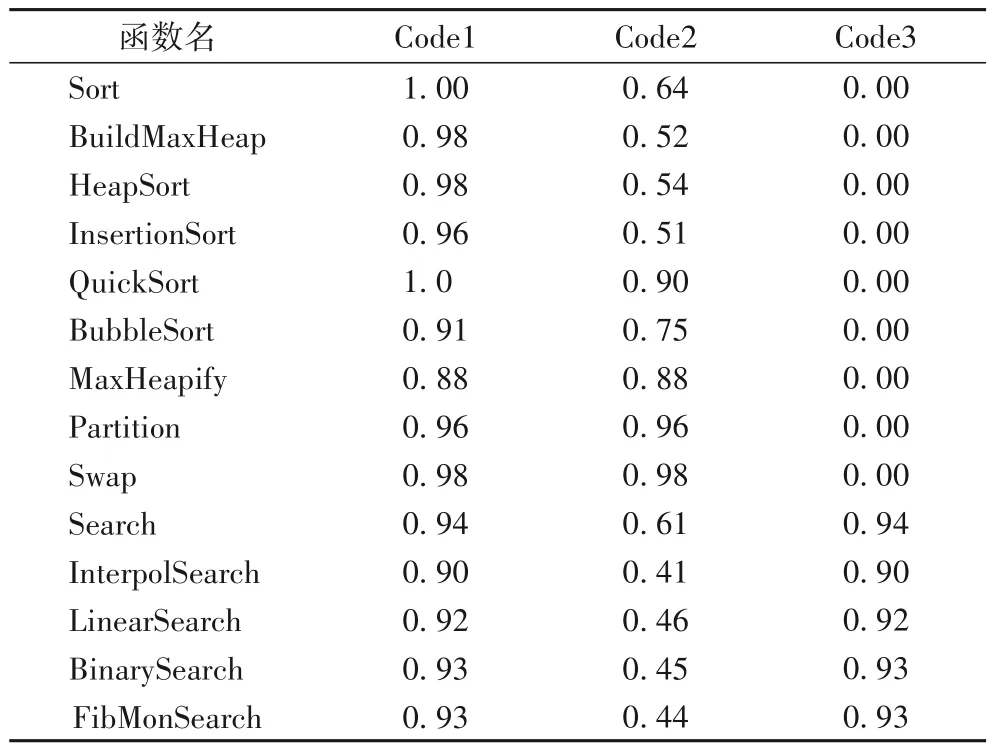
表2 函數調用關系圖匹配結果Tab.2 Function call relationship matching results

表2所示Code1實驗結果中，各函數調用關系相似度均大于0.8，表明Code1的函數調用關系與設計要求一致。可以得出，在設計和實現的函數調用關系一致的情況下，檢測結果與預期結果較為一致，說明在設計特征模型和實際特征模型一致時，本文方法能夠正確匹配對應函數。

Code2 實驗結果中，每個函數都得到匹配結果，而函數Sort 和Search 的函數調用關系相似度均低于0.8，表明Code2雖然實現了所有函數，但函數Sort 和Search 的函數調用關系與設計要求不一致。說明在設計和實現的函數調用關系部分不一致的情況下，本文方法可以檢測到函數調用關系不一致的部分。另外，其他函數的函數調用關系相似度也低于0.8，如所有查找函數和部分排序函數，說明檢測結果雖然與預期方向一致，但部分結果粗糙。這是由于Code2中Sort和Search函數未調用任何函數，使相關的排序算法和查找算法的被調用關系受到影響。導致即使實現了設計要求的函數，比如函數InterpolatSearch、LinearSearch、BinarySearch 等，卻由于被調用關系的不一致，仍被視為匹配度較低，而函數maxHeapify、partition、Swap 未受到影響，檢測結果仍然大于0.8。但是實驗檢測結果仍能說明實現代碼Code2 的函數調用關系與設計要求不一致。

Code3 實驗結果中，排序相關函數的匹配結果均為0，表明Code3 沒有實現排序功能。查找相關的函數匹配結果均大于0.8，表明Code3 完成了查找功能。實驗結果與預期一致，說明在實現代碼只完成部分功能時，仍可以正確匹配實現代碼中功能完成部分的函數，如Code3 中實現查找功能的函數。對于未完成部分函數并不能匹配到對應函數，如排序功能相關的函數。同時，檢測結果能夠說明實現代碼的函數調用關系與設計要求不一致。

由于Code2和Code3的函數調用關系與設計要求不一致，不進行函數內部控制流的驗證。Code1 函數調用關系與設計要求一致，則根據函數對應關系，對函數內部控制流進行對比。表3 列出了設計函數與實現函數控制流圖的相似度以及控制流圖中基本塊不一致檢測結果，基本塊的標號為實際函數中基本塊標號。實驗結果中除函數bubbleSort外，控制流圖相似度均大于0.8，說明這些函數實現邏輯與設計要求一致。實驗14 個函數中，僅有函數bubbleSort 與預期不符，控制流圖匹配準確度達到92.8%，總體實驗結果與預期較為一致。另外，Code1 中函數bubbleSort 的實現邏輯雖與設計要求一致，但由于控制流圖中3 個不同類型基本塊在所有獨立路徑中，導致控制流圖相似度較低，但可通過基本塊檢測結果進行精確驗證。因此實際檢測中應以控制流圖相似度作為參考，并根據基本塊檢測結果進行精確驗證。

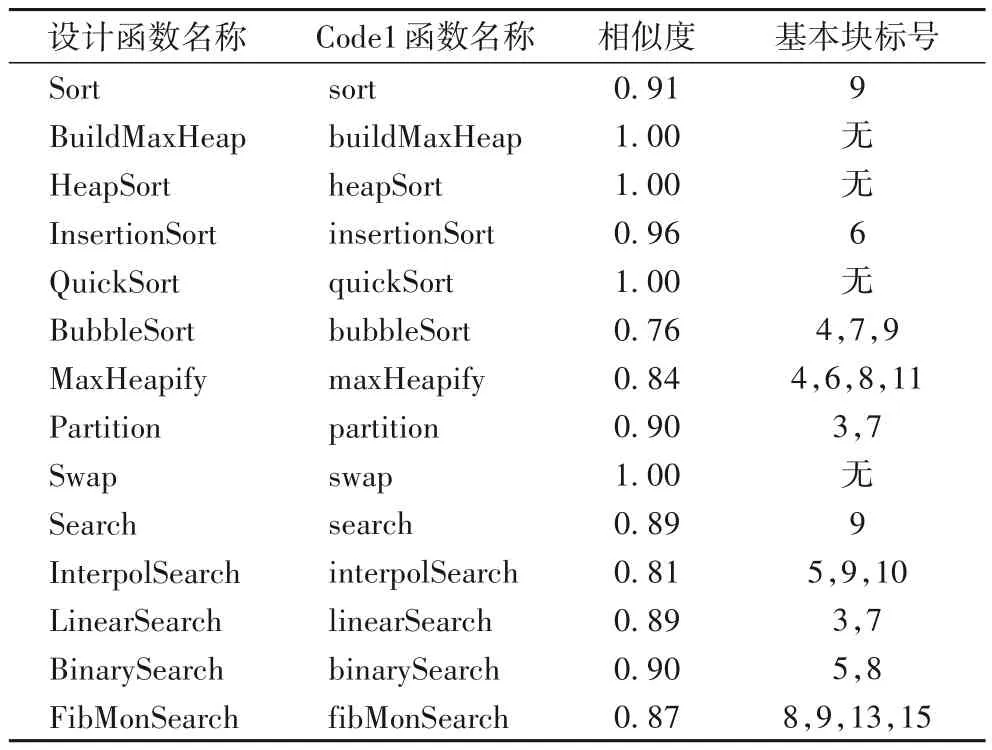
表3 對應函數控制流一致性檢測結果Tab.3 Consistency detection results of corresponding function control flow

4.2 實驗二

設計文檔偽代碼中函數Searh不調用任何函數，建立設計特征模型，與Code1 進行一致性檢測，Code1 為按設計要求完成的代碼。實驗結果如圖8 所示，說明在設計文檔偽代碼不準確時會導致誤判，如函數InterpolatSearch、LinearSearch、BinarySearch、FibMoncianSearch。由于是以設計文檔偽代碼為根據，建立設計特征模型，并以此作為檢測依據，因此在設計文檔偽代碼部分不準確時，會造成不準確部分函數調用關系的誤判，但并不影響其余準確部分功能的檢測。另外，后續的函數內部結構的檢測可以對該問題進行彌補，所以在實際軟件系統一致性檢測中，應保證設計文檔偽代碼的質量，設計文檔偽代碼質量越高，一致性檢測越準確。

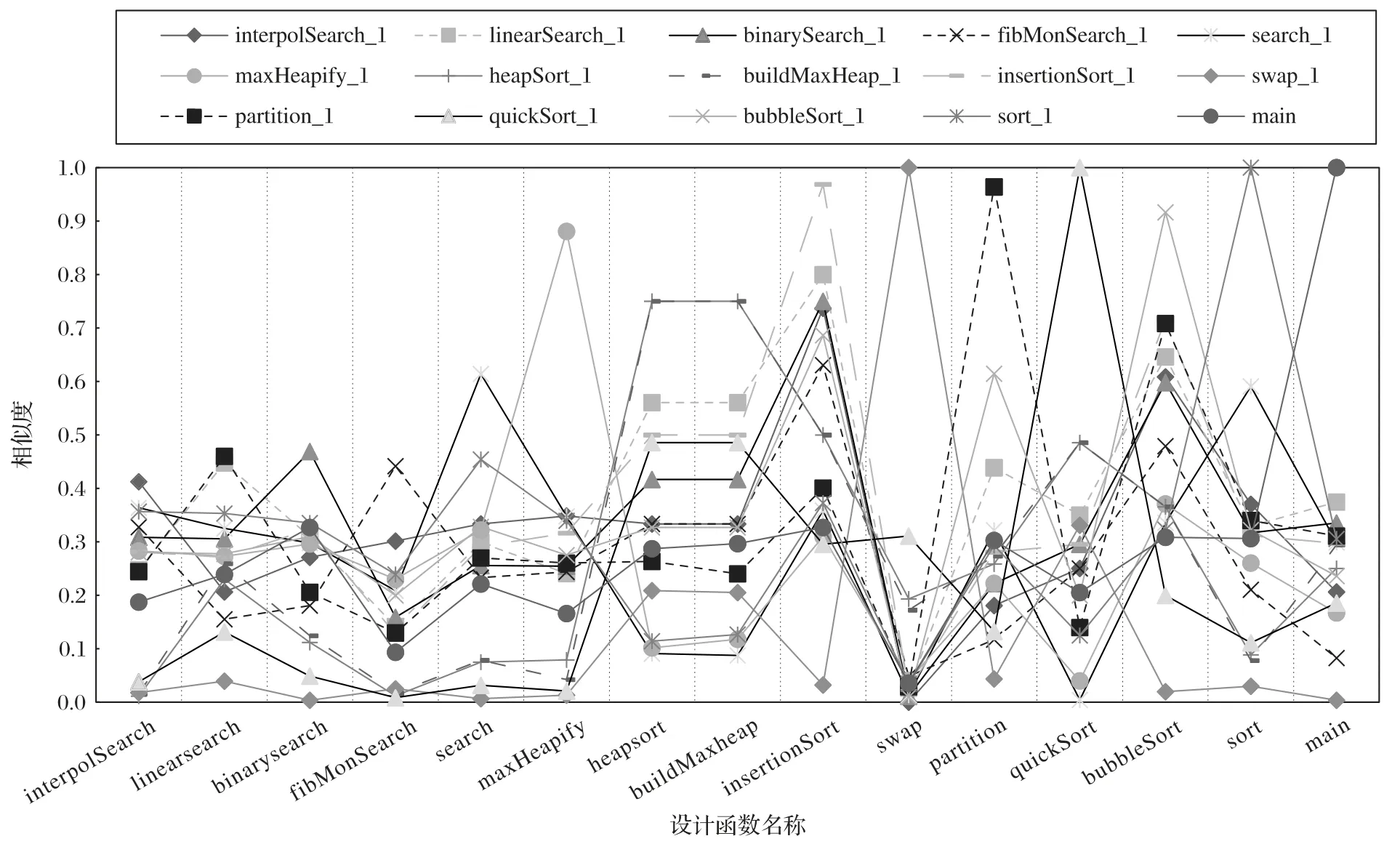
圖8 設計系統與實際系統函數相似度Fig.8 Functional similarity between design system and actual system

5 結語

軟件實現與設計一致性驗證是軟件測試的重要部分之一。本文提出了一種面向設計文檔偽代碼的設計與實現一致性檢測方法，為基于文檔的測試提供一種新的研究思路。從設計文檔偽代碼和程序源代碼自動提取函數特征，建立特征模型，并利用二分圖最大權匹配算法驗證特征模型相似度，獲取函數對應關系，完成函數內部結構的對比，進而完成軟件設計與實現的一致性檢測。該方法不需要大量的模板集，即可獲取一致性檢測結果，提升了一致性驗證的工作效率，并具有更優越的一般性。

但是該方法還存在以下不足：1）在對函數內部結構驗證過程中，并沒有對條件轉移語句的條件進行驗證；2）對基本塊驗證的過程中，沒有考慮其對數據的依賴關系。后續工作可以充分研究基本塊內部結構的驗證，提高驗證的準確度。