一種基于SVM 的多類文本二叉樹分類算法?

宋曉婉 黃樹成

（江蘇科技大學計算機學院 鎮(zhèn)江 212003）

1 引言

支持向量機（SVM）［1-2］是一種基于統(tǒng)計學習理論的用于解決兩類分類問題的機器學習方法，由VAPNIK 和CORTES 于1995 年提出。支持向量機（SVM）在解決小樣本、非線性及高維向量空間中有很好的性能。支持向量機的提出是為了解決兩類分類問題，但是實際的應用中，更多的是對多類分類問題的解決，因此，如何運用支持向量機解決多類分類問題是當前支持向量機研究的方向之一。SVM解決多類分類問題的思路主要有以下兩種：第一種是一次性求解［3］，對多類分類問題通過一個公式求解；第二種是構造多個二值分類器，并根據(jù)不同的組合方式來解決不同的多類分類問題。常用的多類分類支持向量機算法有：“一對一”、“一對多”、“有向無環(huán)圖”和“二叉樹”［4］等。根據(jù)研究表明，第二種方法總體性能較優(yōu)，能更好地解決多類分類問題。

“一對一”算法［5］是在兩類樣本間訓練出一個兩類分類器使其中一個類為正，另一個類為負。該算法訓練速度快，但若某個子分類器存在誤差，就會導致整個分類器出現(xiàn)過學習，并且存在隨著類別的增加兩類分類器的數(shù)量急劇上升及不可分區(qū)域的缺點。

“一對多”算法［6］是在所有類樣本間訓練出一個兩類分類器使其中一個類樣本為正，其余的類樣本為負。該算法所需的兩類分類器的數(shù)量較少，但由于在兩類分類器的訓練過程中會涉及到全部的類樣本，因此分類速度較慢。

“二叉樹”算法是每次將最容易分離出來的類首先分離出來，以此類推直到只剩下一個類為止。二叉樹多類分類算法的分類速度會受到二叉樹結構的影響，完全二叉樹的分類速度較高，因此構造完全二叉樹結構能大大提高二叉樹多類分類算法的分類速度。同時，“二叉樹”算法存在誤差累計，因此應該先將最容易分離的類分離出來，減少誤差的積累。

“有向無環(huán)圖”算法［7-8］是在“一對一”算法的基礎上提出的一種新的學習架構，它將多個“一對一”兩類分類器組合成多元分類器。該算法具有冗余性，不同的DAG 結構會造成部分樣本的分類路徑的不同，從而對分類效果產生影響。

“二叉樹”算法在多類分類中有著很好的擴展性，在多類分類算法中綜合性能較優(yōu)。但存在“誤差累計”及對二叉樹結構依賴的缺點，因此本文主要針對二叉樹結構及分類順序兩個方面改進“二叉樹”算法。

2 基于二叉樹的SVM多類分類算法

2.1 二叉樹SVM算法介紹

二叉樹SVM 算法［9-10］主要思路：先將所有的類分成兩個子類，再將這兩個子類分別劃分成兩個次子類，以此類推，直到所有節(jié)點只包含一個類為止。二叉樹多類分類算法的分類速度會受到二叉樹結構的影響，完全二叉樹的分類速度較高，因此構造完全二叉樹結構能大大提高二叉樹多類分類算法的分類速度。現(xiàn)有的二叉樹多類分類算法只是隨機的生成二叉樹結構，所以，合理的構建二叉樹結構是提高二叉樹SVM算法分類速度的關鍵。

二叉樹SVM 算法存在“誤差累計”的缺點，上層節(jié)點的分類結果對整個算法分類性能有著極大的影響，有效的分類順序是提高二叉樹SVM 分類精確度的關鍵。常用的二叉樹生成思路有以下兩種：1）根據(jù)類中樣本的分布情況進行劃分，先將類中樣本分布范圍較廣的類分離出來，主要通過計算各類的超球體的體積來衡量類樣本分布情況，超球體體積越大，分布范圍越廣。2）根據(jù)兩類間的距離進行相似度判斷，一般利用歐氏距離來計算兩類之間的距離，距離越小，相似度越大，應該最先分離出來。

2.2 相關定義

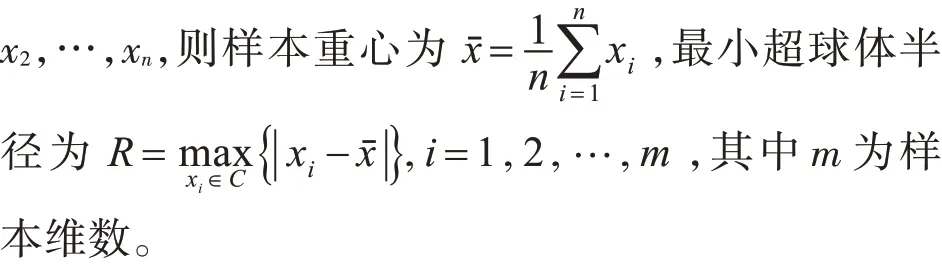
超球體SVM［12～13］主要思想：在非線性系統(tǒng)中，通過映射函數(shù)將低維空間的特征向量映射到高維空間進行類的劃分。在高維空間中，以盡可能小的超球體半徑包含更多的樣本，考慮到散落在球面附近的樣本，引入松弛變量§m，i，并計算覆蓋樣本的最小超球體的半徑及球心。

定義2：歐氏距離［14］。也稱歐幾里得距離，主要用于計算兩點之間的真實距離，m 維空間中點i和j的距離為

在判別兩類之間的分離程度時，可以使用歐氏距離法、超球體SVM 或者兩種方法的結合，但都不能準確地反映類的分布情況。單獨使用歐氏距離法進行類的相似度的判斷沒有考慮類中樣本的分布情況，單一使用超球體SVM 方法只是考慮類的樣本的分布情況卻忽略類間的相似度的判斷。采用歐氏距離和超球體SVM 方法結合進行類的相似度判斷在精確度上有了一定的提升，但是依然存在一定的問題。為了解決這一問題，本文對類內和類間相似方向進行了改進提出了類間相似度量數(shù)的概念。同時，提出了一種二叉樹結構生成算法，使二叉樹在總體上為偏二叉樹，在局部為完全二叉樹或者近似完全二叉樹，從而提高二叉樹分類效率及分類精度。

3 改進的二叉樹SVM多類分類算法

3.1 相關定義

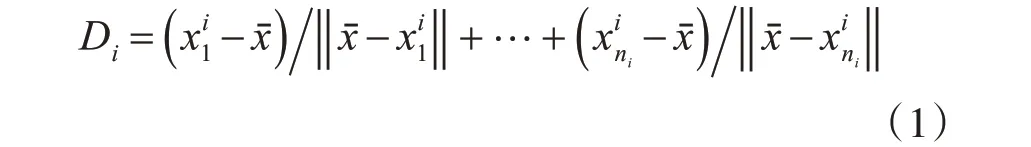
其中，xˉ是根據(jù)文獻［15］中式（10）、（15）得到的每類樣本所在最小超球體的中心。

定義4：類間相似度量數(shù)。假設類i 和類j 的最小超球體半徑分別為ri和rj，那么類i 和類j 的類間相似度量數(shù)為

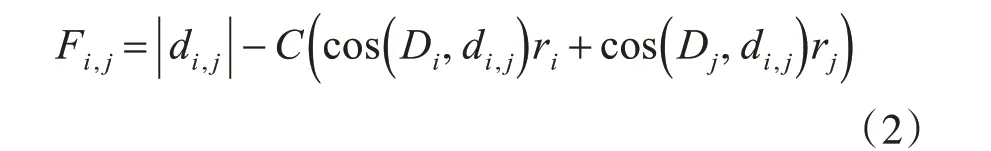
其中，|di，j|為從類i 中心向量到類j 中心向量的歐氏距離，C 為參數(shù)值，其值根據(jù)樣本的分布情況進行調整，默認情況下取值1，F(xiàn)i，j越大越不相似，應該最先分離出來。

對圖1 中的兩個圖的情況進行觀察可以發(fā)現(xiàn)：左圖的類間距較小，但類之間的分布較遠；而右圖的類間距較大，但類之間的分布較近。采用距離或類間相似方向來進行兩類之間的相似度判斷，都不能達到比較好的效果，而采用本文提出的類間相似度量數(shù)能在類間距和類的分布情況兩種因素上綜合考慮，從而獲得更有效的分類順序，提高分類精確度。

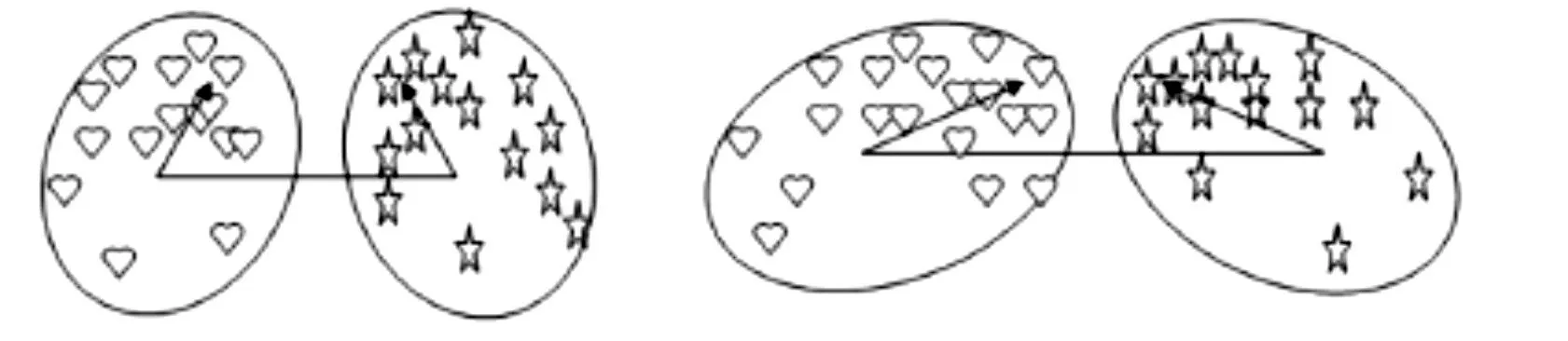
圖1 左右兩圖表示兩類間距離及類間相似方向

3.2 算法步驟

定義類平均類間相似度量數(shù)：

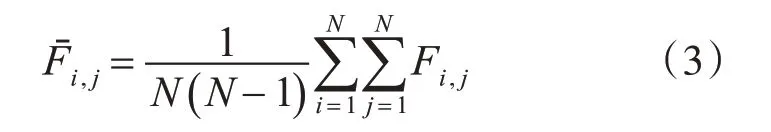
1）對于N 類問題，定義集合G、G1、G2、G3、G4和G5，NG、NG1、NG2、NG3、NG4、NG5（NG、NG1、NG2、NG3、NG4、NG5分別表示集合G、G1、G2、G3、G4和G5中的類編號的個數(shù)）。首先對所有類樣本從編號1 到編號N 進行編號，并放到集合G 中。然后根據(jù)式（1）～（3）計算所有類樣本的類間相似度量數(shù)Fi，j（i=1，2，…N，j=1，2，…N，i≠j）和Fˉi,j。

2）如若NG=2，那么把類編號較小的類作為左子樹，類編號較大的類作為右子樹，算法結束。

3）根據(jù)式（1）～（2）計算集合G中的每一個類到其他類的Fi，j，并統(tǒng)計每一個類的Fi，j小于 λFˉi,j的個數(shù)（λ根據(jù)樣本分布情況進行值的調整，是一個大于零的參數(shù)），記作Sumi（i=1，2，…N）。

4）找出最大的Sumi，如果存在相同的Sumi，則選擇類編號較小的類樣本。如果Sumi=NG，則將集合G 中的所有類編號放到集合G3中，轉5）。否則，將類編號i 放到集合G1中，并將滿足Fi,j＜ λFˉi,j(j=1,2,…N,i ≠j)的類編號放到集合G1中作為二叉樹的左子樹，將剩下的類編號放到集合G2中作為二叉樹的右子樹，并將集合G1中的所有類編號放到集合G3中，轉5）。

5）若NG3=2，那么把類編號較小的類作為左子樹，類編號較大的類作為右子樹，算法結束。

6）找出Fi，j值最小的兩個類i 和j，并將它們按照類編號的大小放到集合G4中。在剩下的類中找出與集合G4中各類的Fi，j和最大的類標號，并將其放到集合G5中，令G3=G3-（G4∪G5）。若NG3=0 則轉8）。

7）計算集合G3中的各類到集合G5的各類的Fi，j和，找出最小Fi，j和的類編號，并將其放到集合G5中，令G3=G3-（G4∪G5）。若NG3=0則轉8）。否則，若NG3=1，計算集合G3中的類與集合G4和G5中各類的Fi，j和，將其放到Fi，j和較小的集合，比較NG4和NG5大小，若NG4＞NG5，則將集合G4和G5中的類編號進行交換，轉8）。否則，計算集合G3中的各類與集合G4中各類的Fi，j和，找出最小Fi，j和的類編號，并將其放到集合G4中，令G3=G3-（G4∪G5）。

8）重復7）。

9）集合G4和G5分別作為二叉樹的左右子樹，并將左子樹進一步劃分為兩個次子類，令G3=G4，轉5）。

10）對右子樹劃分為兩個次子類，令G3=G5，轉5）。

11）若NG2=1則算法結束，否則將集合G2中的類編號放到集合G中，轉2）。

經過以上實驗步驟，可以使更容易分離出來的類首先分離出來，提高分類精確度，同時使生成的二叉樹結構根據(jù)樣本數(shù)據(jù)分布情況的變化而變化，在總體上是一顆偏二叉樹結構，局部是一顆完全或近似完全二叉樹結構，具有較高的分類速度。

4 仿真實驗

實驗采用的數(shù)據(jù)集包括UCI 數(shù)據(jù)庫中的Glass Identification 和Optdigits，以 及Statlog 數(shù) 據(jù) 庫 中 的Satimage 和Letter，實驗數(shù)據(jù)集信息見表1。算法采用Matlab 和VC++混合編程，并且是在LIBSVM 工具包的基礎上進行修改的。實驗采用RBF核函數(shù)，固定的最優(yōu)參數(shù)（C，r）是經過網格搜索法得到的推廣精度最高的C和r參數(shù)。為了證明本文所提出的算法具有較好的分類性能，選取一對多SVM（One-versus-rest，OVR）和一對一SVM（One-versus-one，OVO）在四個數(shù)據(jù)集上進行對比實驗，實驗結果見表2和表3。

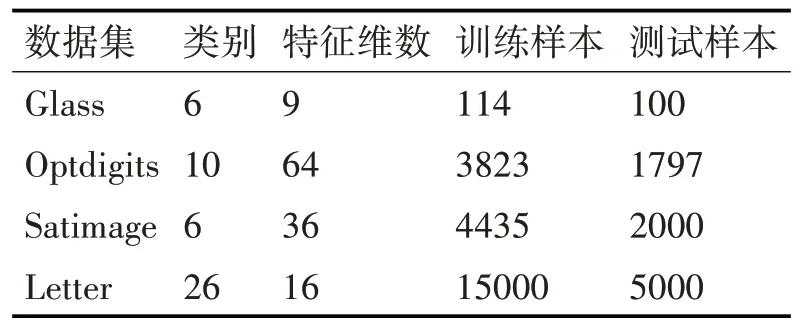
表1 數(shù)據(jù)集信息表

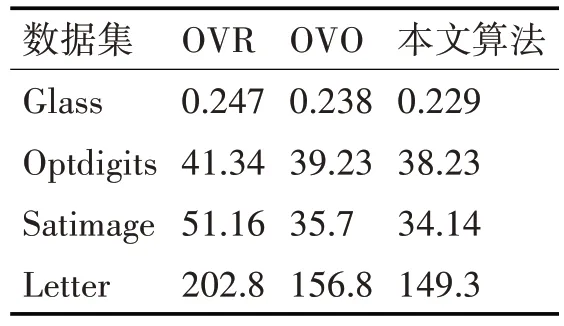
表2 分類速度比較表/s

表3 分類精度比較表/%

通過以上實驗得出結論：在相同的測試條件下，不同的分類算法會得到不同的分類結果。由表2 可知，本文算法的分類速度較OVR 和OVO 算法快，原因是：二叉樹多類分類算法構造的兩類分類器較少，且在訓練過程中所涉及的樣本數(shù)量也逐漸減少。同時，本文算法使生成的二叉樹結構總體上是一顆偏二叉樹，局部是一顆完全或近似完全二叉樹結構，大大減少所需計算的二值分類器數(shù)量，進一步提升分類速度。通過表3 可以看出，本文算法在分類精度方面也有了一定的提升，文中提出的類間相似度量數(shù)能更準確地將更容易分離出的類分離出來。

5 結語

本文介紹了當前支持向量機解決多類分類問題的一般思路及二叉樹SVM 多類分類算法的原理，并分析現(xiàn)有二叉樹SVM 存在的問題。并針對存在的問題提出了一種改進的二叉樹SVM 多類分類算法，該算法能大大減少“誤差累計”，提高分類精度。同時，使生成的二叉樹總體上是一顆偏二叉樹，局部是一顆完全或近似完全二叉樹結構，提高分類速度。通過在四個數(shù)據(jù)集上進行實驗，實驗結果表明，本文算法在分類速度及精度上都有了一定的提升，具有一定的可行性。