基于綜合權重分析的柔性微夾持器可靠性分配方法

伍建軍，劉 拓，朱 迅

（江西理工大學 機電工程學院，贛州 341000）

0 引言

柔性微夾持器作為精密儀器，在生物工程、醫療科學、精密加工等領域有著廣泛的應用。其工作原理主要是通過柔順機構形變產生的微位移控制夾持器鉗口的張合，用來夾取、運送和裝配微小物品。由于柔性微夾持器的工作條件特殊，因此對可靠性要求非常高[1,2]。研究發現影響柔性微夾持器可靠性的主要原因是各個連接處柔性鉸鏈產生的疲勞損傷。就損傷位置和損傷程度進行有效、及時地識別，是設計柔性微夾持器的重要依據。目前國內對柔性微夾持器的研究主要集中在其性能和結構的優化設計上。

胡俊峰[3]提出了一種基于響應面法的微操作平臺多目標優化方法，結合響應面法，以平臺的放大倍數和固有頻率為目標，使用多目標遺傳算法進行結構優化，解決了微操作平臺放大倍數和固有頻率相沖突情況下的優化難題。李姣[4]針對連續體結構柔順機構進行拓撲優化，提出了一種可以優化連續體柔順機構拓撲結構的方法，這種方法加入了的互應變能和應變能，為柔順機構的多目標可靠性穩健性設計打下了基礎。[5]聶鵬飛采用了基于證據結構的非概率穩健優化設計方法。對柔性微夾持器非概率穩健優化過程中的參數不確定性統一采用證據理論結構進行表征，推導出了判斷優化設計參數優劣的判斷準則。

查閱文獻可知，目前對柔性微夾持器的可靠性的研究較少。因此，針對柔性微夾持器受到復雜環境影響導致可靠性降低的問題，本文以某型號柔性微夾持器為例，首先對柔性微夾持器進行有限元分析，由應力云圖找出應力集中最嚴重的幾個部位進行重點分析。以模糊層次分析法為基礎結合熵權分析求出分配權重，引入博弈理論計算出分配的綜合權重，進行可靠性分配，得出系統的整體可靠度的分配方案。結果表明，該方法能夠有效的進行可靠性分配。對柔性微夾持器的設計及可靠性評估具有指導意義，具有工程實際意義。

1 柔性微夾持器關鍵位置的識別

柔性微夾持器是由若干柔性鉸鏈組合成的整體。相對其他鉸鏈，直圓型切口柔性鉸鏈綜合性能較好，有更大的位移范圍。因此柔性微夾持器廣泛使用直圓型切口柔性鉸鏈。柔性微夾持器在工作過程中，各個連接處的柔性鉸鏈發生不同的程度形變，不同部位鉸鏈的形變量不同導致鉸鏈上的應力集中程度不同，其中應力集中過大導致的損傷失效是影響整體可靠性的主要原因。

首先確定鉸鏈最容易失效的部分，模擬實際工作情況，通過ANSYS Workbench進行有限元仿真，對柔性微夾持器的底端面進行固定，在中間施加向上的力，其應力云圖如圖2所示，由圖可見，柔性微夾持器在工作的過程中不同的鉸鏈連接處應力大小有差異，應力主要集中在中間部分的柔性鉸鏈圓弧上，這些地方的應力集中程度最大，損傷程度也最為嚴重，其中各個鉸鏈應力大小的不同對柔性整體可靠性的影響也不同。為此，選取應力集中最大的5個部位進行重點分析。

圖1 柔性微夾持器

圖2 柔性微夾持器應力云圖

2 綜合權重可靠性分配方法

柔性微夾持器綜合權重可靠性分配方法是為了保證柔性微夾持器可靠性分配結果更有可信度。本文所用的綜合權重分析法使用博弈理論同時融合了模糊層次分析法和熵權分析法兩種主客觀分配法優點[6～8]。是將帶有主觀評判的模糊層次分析法和帶有客觀評判的熵權分析法相結合的一種新的可靠性分配方法。具體步驟如下：

1）建立模糊層次分析結構模型

以柔性微夾持器系統的整體可靠性作為目標層。

以影響柔性微夾持器系統可靠性的復雜環境因素，外物碰撞、環境腐蝕、材料老化、長期載荷和疲勞失效等5個環境因素作為準則層[9]。

以有限元分析篩選出的應力集中最大的5個子系統柔性鉸鏈作為方案層。

通過建立模糊層次分析模型，制定出能夠滿足柔性微夾持器系統整體可靠度要求的可靠性分配方案，其層次結構模型如圖3所示。

2）建立三標度優先判斷矩陣F

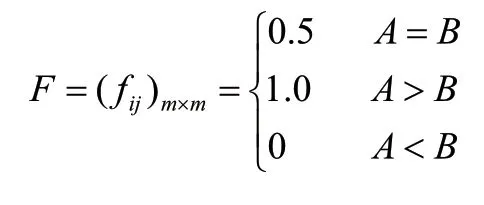
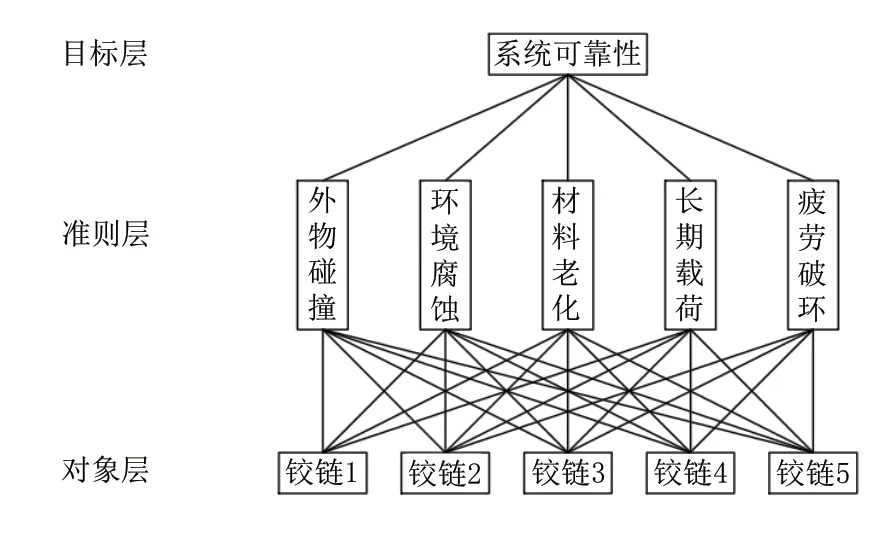
圖3 層次分析結構模型

其中，A和B分別表示fi和fj的重要程度，m表示準則層單元的個數。

3）將優先判斷矩陣F=（fij）m×m轉換為模糊一致性判斷矩陣Q。

整理后得出模糊一致性判斷矩陣：

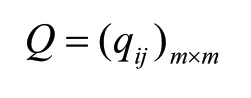
4）使用歸一法求權重向量。模糊一致性矩陣Q=（qij）m×m每行元素之和為：

剔除對角線元素的元素總和為：

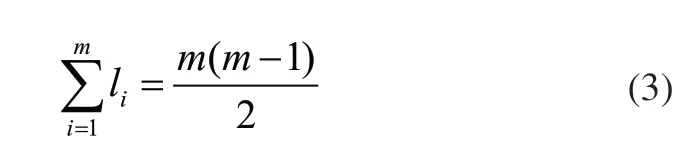
由于li為指標i的相對重要性，對li進行歸一化處理得到指標權重：

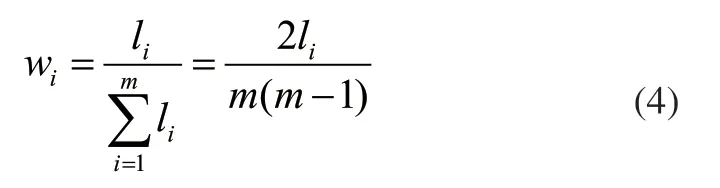
從而得出權重向量為：

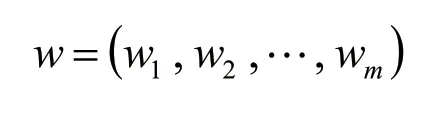
5）計算組合權重向量。運用上述的步驟，求出準則層影響相對于目標層的權重向量ωi=（ω1，ω2，…，ωm），對象層在準則層影響下的權重向量vi=其中n為對象層單元的數量。vi=（v1，v2，…，vn），最終得出對象層單元相對目標層的組合權重向量為：

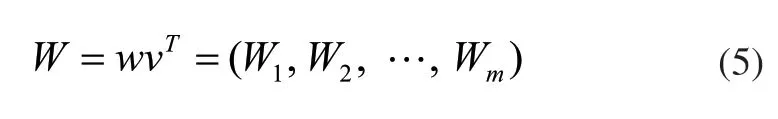
6）熵權分析

構建初始判斷矩A。

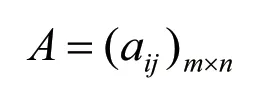
矩陣中，m，n分別為評價對象和評價指標的個數，aij為在第j個因素影響下的第i個對象所對應的評價值，將aij進行歸一化處理得到判斷矩陣R：

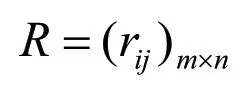
計算出每個評價指標的熵權值：

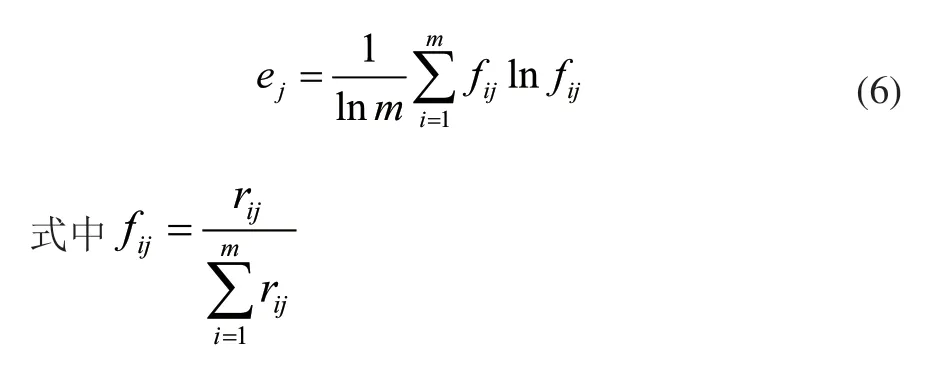
引入差異系數Gj：

從而得出指標的熵權為：

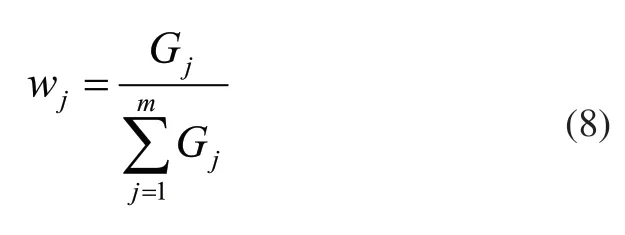
通過熵權計算出影響因素的權重w：

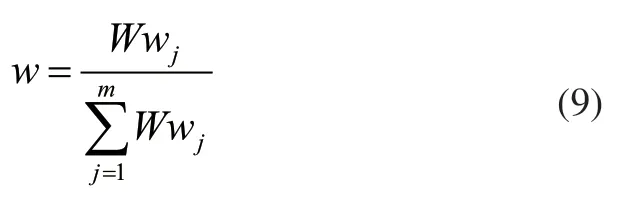
7）引入博弈理論進行綜合賦權，將上述兩種權重向量進行組合，得出新的權重向量集：

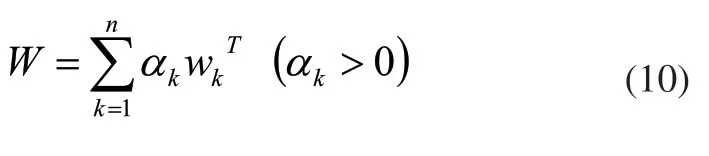
使w與各個wk的離差極小化，即：

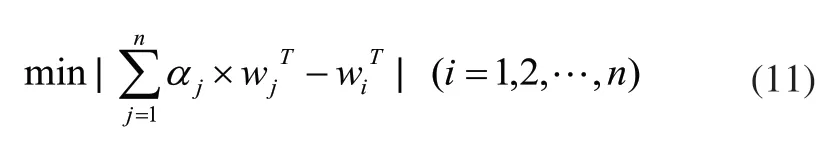
式(11)達到最優化的一階導數條件為：

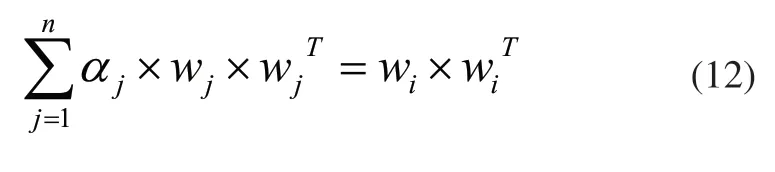
將式(12)上進行矩陣運算求出（a1，a2，…，an）同時進行歸一化處理：

得到綜合權重：

8）以綜合權重向量為基礎分配可靠性指標R。可靠性指標R和對象層各單元分配的的權重有如下關系：

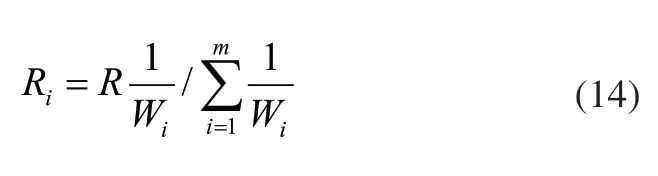
式中，Ri為第i個單元的可靠指標；Wi為第i個單元的綜合權重。

3 串聯鉸鏈系統的可靠性分配

本文選用應力集中程度最大的5個柔性鉸鏈進行重點分析，將柔性為夾持器簡化為串聯鉸鏈系統，建立柔性鉸鏈串聯模型和抽象簡圖，如圖4、圖5所示。

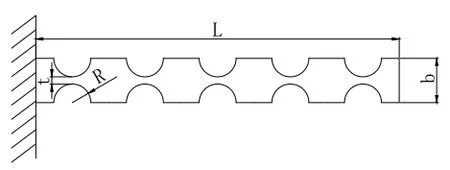
圖4 串聯柔順機構結構圖

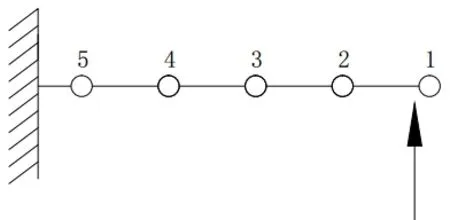
圖5 串聯柔順機構抽象簡圖

模擬實際工況，在輸入端施加一個恒定的力F，各個柔性鉸鏈子系統將會發生不同的形變，其過程可以看做同一個柔性鉸鏈施加不同的力所發生的形變，使用ANSYS workbench17進行疲勞仿真實驗。取5個試件分別在正壓力為40N、50N、60N、70N和80N時進行疲勞仿真實驗，疲勞壽命見表。5個試件在不同載荷水平下的疲勞仿真實驗。實驗結果如表1所示。

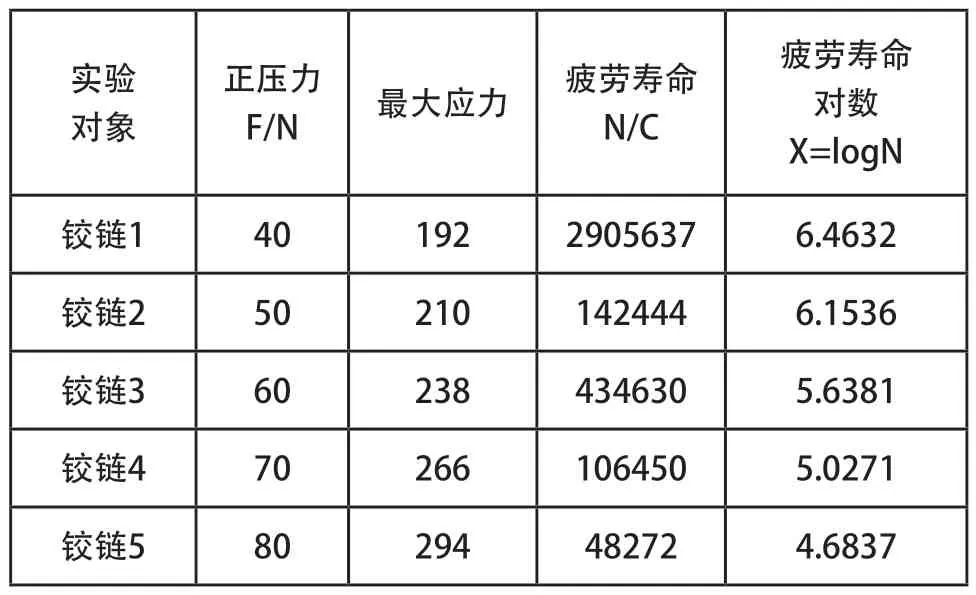
表1 不同載荷水平下的疲勞仿真實驗

根據模糊層次分析模型以及三標度關系的關系，結合專家評定指導意見結果，比較各個因素對系統整體可靠度的影響程度。得出如下影響柔性微夾持器可靠性的權重關系。如表2所示。

表2 各因素對可靠性的影響程度

比較每兩個柔性鉸鏈在5個影響因素的影響強弱，轉換成矩陣K：

根據K中的數據，求行和得：

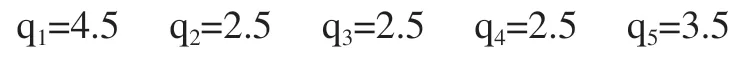
將矩陣K進行模糊一致性轉化得到矩陣Q：

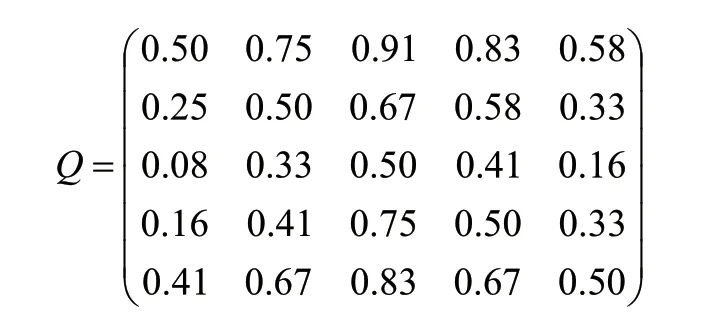
由式(2)～式(4)，計算得出準則層中影響因子相對目標層的權重W：

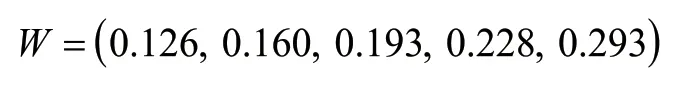
在準則層不同因素的影響下，比較對象層各單元之間的相互權重關系。

根據柔性微夾持器各單元的具體情況及專家經驗，將影響程度由強到弱分別以（A，E，I，O，U）分別賦予不同的標度，根據影響程度得出如下相對關系，如表3所示。

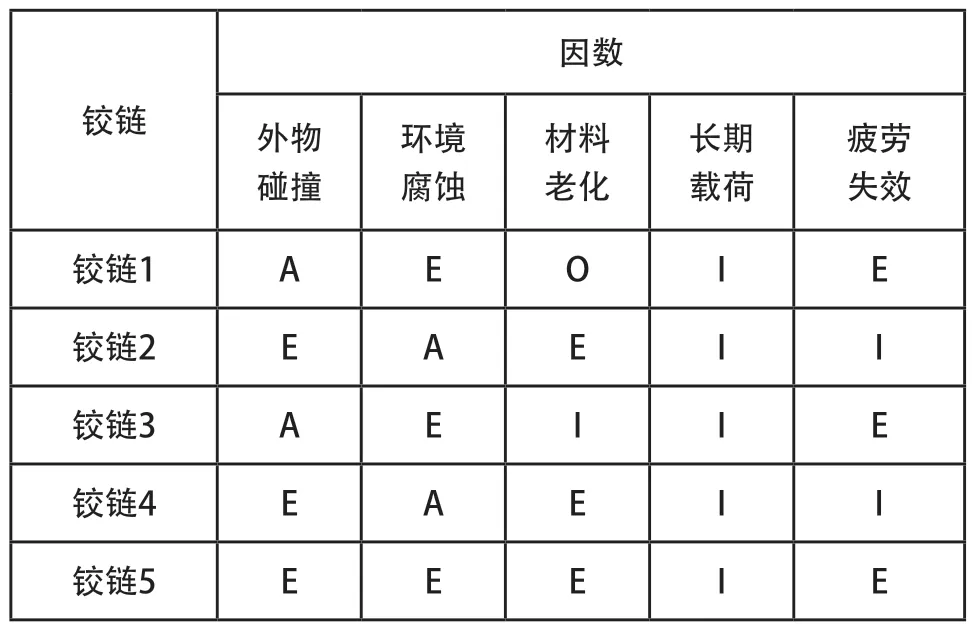
表3 不同因素對鉸鏈影響評價表

利用模糊層次分析法的步驟，可將這些不同程度的影響權重關系轉化成優先關系矩陣M。

其中外物碰撞對鉸鏈子系統優先關系矩陣為M1：

重復上述步驟依次得出環境腐蝕對子系統優先關系矩陣M2，材料老化對子系統優先關系矩陣M3，長期載荷對子系統優先關系矩陣M4，疲勞失效對子系統優先關系矩陣M5。

由第4步，得出由于準則層單元影響條件下，對象層各單元相對于準則層各單元的權重v1，v2，v3，v4，v5，將其轉化為矩陣V：

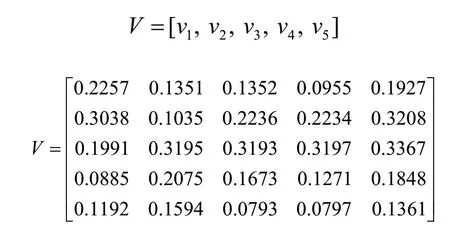
由式(5)所知，計算出對象層相對目標層的綜合權重即鉸鏈子系統分配的綜合權重：

計算熵權指標權重，按照上述步驟建立優先判斷矩陣A，并將其進行模糊轉換得到模糊一致性矩陣Q：

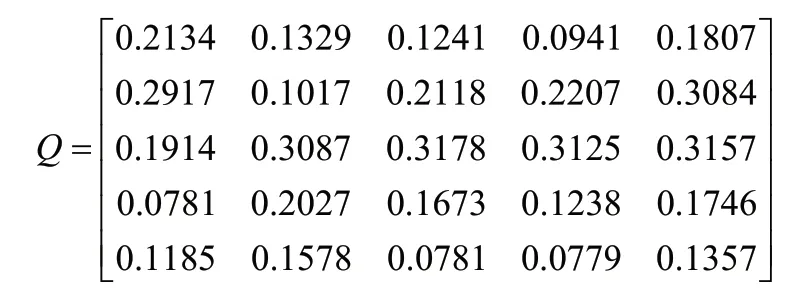
運用式(6)～式(9)得出熵權權重W：

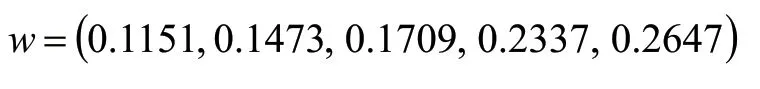
引入博弈理論，運用式(10)～式(14)將上述兩種權重綜合分析得出綜合權重W*：

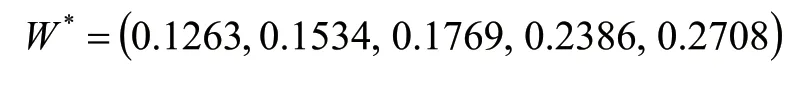
以綜合權重為基礎對可靠性指標進行分配。當柔性微夾持器的可靠度要求為R=0.95時，根據式(15)，分別求出三種權重分配的可靠度R1，R2，R3：

因此，通過上述系列計算得出由5個鉸鏈單元組成的串聯鉸鏈系統的整體可靠度為R'。

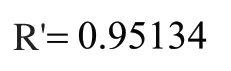
由綜合權重分析結果可以看出可靠性分配方案基本滿足設計指標所需的要求。鉸鏈5應該分配相對較高的可靠性，這與實際工作中下施加在鉸鏈5上的載荷最大，從而導致應力集中最嚴重的的情況相符。而施加在鉸鏈1上的載荷相對較小，失效的概率較低，所以分配的可靠度較低。

4 結語

本文基于綜合權重分析法，以柔性微夾持器為例，運用簡化模型研究了柔性為夾持器的可靠性分配方法。通過引入博弈理論進行綜合權重分析，解決了傳統的模糊層析法、熵權法分配權重具有主觀性與客觀性，使得對相同指標分配的權重存在較大差異的問題。

結果表明，使用綜合權重分析法對簡化模型的可靠性進行分配，提高了可靠性分配結果的合理性，同時也增加了分配結果的可信度，具有有較好的實用性。通過簡化模型的分配方案對柔性微夾持器復雜系統的設計提供有效的依據。