旋轉矩陣在移動機器人建模教學中的應用

武星 鄒婷

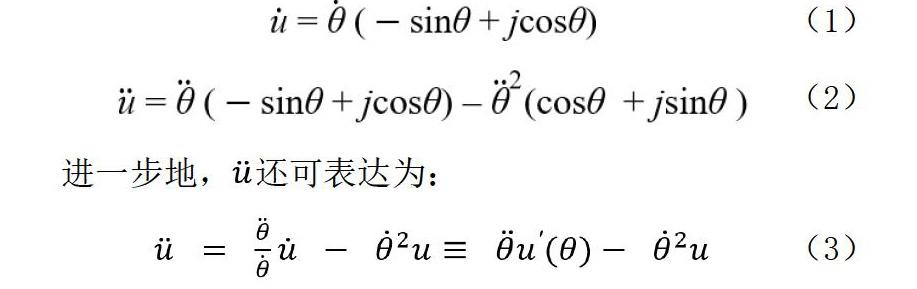
摘? 要 移動機器人因其可在較大工作空間完成特定作業任務而受到廣泛應用。在其平面運動學教學過程中，很多教科書采用單位復數u（θ）≡ejθ作為剛體運動學建模的工具。然而，該算子難以明顯地反映出旋轉變換的幾何學和運動學的物理含義。為此，將三維旋轉矩陣簡化到二維空間，并用于移動機器人的運動學建模教學過程。該教學思路符合多剛體系統建模和矩陣計算分析的整個理論框架和求解方案，有利于不同專業背景學生的理解和掌握。

關鍵詞 移動機器人;平面運動學;機器人建模;旋轉矩陣

中圖分類號：G642? ? 文獻標識碼：B

文章編號：1671-489X（2020）08-0087-03

1 引言

近年來，隨著以“工業4.0”和“中國制造2025”為代表的第四次工業革命的興起，人工智能與機器人正發生不斷深入的有機融合，廣泛應用于工業、農業、服務業以及科研、教育領域。與固定于某一位置操作的工業機器人相比，移動機器人能夠通過傳感器感知環境和自身狀態，實現在有障礙物的環境中面向目標的自主運動，并完成一定的作業功能[1]。移動機構決定了移動機器人的運動能力和特性，主要有輪式、履帶式、腿足式和蠕動式等。輪式移動機構具有結構簡單可靠、能量利用率高、高速穩定、易控性和操作性好、通過性和平順性好等優點[2]。其中，差速輪式移動機器人（Differential-driving Wheeled Mobile Robots， DWMR）的一個顯著優勢是不需要額外的轉向機構，僅通過改變兩個驅動輪的行走速度即可操縱機器人的運動方向[3]，因此在機器人工程專業人才培養時成為一個典型的移動機器人教學對象。

為了適應“中國制造2025”制造強國戰略對智能制造高端技術人才的迫切需求，南京航空航天大學面向全校不同專業的學生適時開辦了“機器人科學導論”國際課程。來自不同專業背景的學生在“矩陣論”“理論力學”“機械原理”和“控制工程基礎”等領域知識方面具有較大差異。為了保證落實“寬口徑、重基礎”的智能制造復合型人才培養目標，需要深入研究面向跨專業學生群體的移動機器人建模教學方法。

2 教學現狀

移動機器人作為機器人的一個分支，其教學方法仍可沿用工業機器人的多體系統運動學/動力學教學方法。對于僅在地面運動的輪式機器人，特別是在結構化人工環境中運行的場景，其運動過程可簡化為平面運動方式。在其平面運動學教學過程中，很多教科書[4-5]都采用了單位復數u（θ）≡ejθ的工具，其中j為虛部。并且，當θ=θ（t）時，有：

進一步地，還可表達為：

公式（1）說明的向量形式垂直于u（t）的向量形式。公式（2）和（3）說明自然分解為兩個正交分量，第一項和第二項分量分別垂直和平行于向量u（t）。

雖然u（θ）作為一個算子，通過逆時針旋轉θ角度，恰當地將一個復數z=x+jy變換到另一個新的復數，然而在筆者看來，這個算子難以明顯地反映出旋轉變換的幾何學和運動學的物理含義。在教師給學生講解平面運動學的教學過程中，如果可引入二維旋轉變換矩陣，那么在實平面上采用復數表達這些點及其變換，則是一個本不需要的技巧。

3 旋轉矩陣

在大多數高校，機器人專業課程一般開設于大三下學期或大四上學期。為了便于學生理解移動機器人的平面運動學建模過程，教師可首先回顧大學“理論力學”中的剛體運動學教學內容。當描述某剛體B在三維空間中的方位時，設置一直角坐標系{B}與此剛體固連。用坐標系{B}的三個單位主向量xB、yB、zB相對于慣性坐標系{A}的方向余弦組成的3×3階矩陣表示剛體B相對于坐標系{A}的方位[6]：

其中，稱為旋轉矩陣，上標A代表參考坐標系{A}，下標B代表與剛體B固連的坐標系。由于矩陣的三個列向量、、都是單位向量，且兩兩相互垂直，滿足以下正交條件：

其次，教師將移動機器人作為建模對象引入教學過程中。當輪式機器人在地面上運動時，建立如圖1所示的三維運動坐標系。其中，x軸指向移動機器人的前進運動方向，y軸指向移動機器人的側向，z軸垂直于地面向上。定義移動機器人繞z軸逆時針旋轉α角度的運動為偏航運動，繞y軸逆時針旋轉β角度的運動為俯仰運動，繞x軸逆時針旋轉γ角度的運動為翻滾運動，則偏航運動、俯仰運動和翻滾運動的旋轉矩陣分別為：

最后，如果輪式機器人運行在地面足夠平坦的結構化環境中，則可將其運動過程簡化為平面運動方式，沿z軸的垂直運動以及俯仰運動和翻滾運動可忽略。因此，三維空間中的剛體運動學可簡化為平面運動學。相應地，偏航運動可簡化為在平面內繞z軸逆時針轉動的二維旋轉矩陣：

正如Bottena等所指出[7]，二維旋轉矩陣Q2還可表示為：

Q2=cosα12+sinαE2? ? ? ? ? ? （11）

其中，12為二階單位矩陣，E2為：

并且，E2可視為在平面內繞z軸逆時針旋轉90°的二維旋轉矩陣，即E2=Q2（90°）。

由式（10）和（12）可知，輪式機器人在平面內繞z軸轉動的二維旋轉矩陣在數學形式上非常簡單，在物理意義上十分明確，在幾何圖示時易于表達。這種對旋轉矩陣從三維到二維的降維處理，使得輪式機器人建模教學對學生的背景知識要求不高，僅需要二維的剛體運動學知識和基本的矩陣論概念，有利于學生深入理解和熟練掌握作為建模工具的二維旋轉矩陣。

4 機器人教學應用

為了進一步說明二維旋轉矩陣在平面運動學教學過程中的應用，本文以DWMR的運動學建模為例進行詳細分析。在差速驅動結構中，兩個獨立驅動的驅動輪同軸安裝于尾軸的兩側，一個萬向隨動輪自由鉸接在移動機器人底盤前端的中心線上。為了方便運動學分析和多剛體建模，DWMR的機構簡圖表示為由多個轉動副連接的機械剛體系統，如圖2所示。DWMR底盤由一個T型剛體表示，兩個驅動輪通過穿過點O1和O2的旋轉軸活動連接于底盤。一個萬向輪支架通過垂直轉向軸連接于底盤P點。萬向隨動輪通過一個穿過點O3的水平轉軸安裝于萬向輪支架上。