多向不規則波浪的確定性模擬

羅麗，柳淑學*，李金宣，王磊

( 1. 大連理工大學 海岸與近海工程國家重點實驗室，遼寧 大連 116024)

1 引言

真實的海浪是多向不規則的波浪，其方向分布對波浪傳播特性及波浪與結構的相互作用有著重要的影響。為了準確地研究海洋環境及海洋工程中的波浪特性，有必要將實測的波浪歷時過程線（波浪時間序列）進行再次模擬和重現，即波浪的確定性模擬。

一些學者對二維不規則波浪的確定性數值或物理模擬取得了較好的結果。Baldock 和Swan[1]基于對實測波浪在空間和時間上進行傅里葉級數展開，在數值模型中求解了具有非線性特性的單向不規則波浪，成功的通過數值模擬方法重現了物理實驗的波浪過程線。裴玉國等[2]利用一個基本波列和一個瞬態波列進行線性疊加的方式對實測的畸形波進行了定點模擬生成，模擬產生的波列和實測的波浪時間過程吻合良好。Liang 等[3]基于快速傅里葉變換（FFT）方法，將二維不規則波分解為具有不同初始相位的組成波，數值重現了不規則波過程。崔成等[4]基于單波列疊加模型，在完全非線性的數值波浪水槽對不規則的波列進行了確定性模擬。Finnegan 和Goggins[5]通過FFT 方法將大西洋上實測的一點海浪表示為線性波浪疊加的形式，將此疊加的波面作為二維計算流體動力學（CFD）數值模型的入射邊界，并將數值模型輸出的波浪過程線分別與濾波分析后的波浪過程線及實測的海浪過程線進行了對比分析，驗證了重現波浪的準確性。沈王剛[6]基于非線性波浪分離方法，在二維勢流數值波浪水池中確定性重構了具有反射成分的強非線性波浪的波動過程。

然而，上述研究大都針對的是單向不規則波浪，而真實的海浪是多向不規則的。但是關于多向不規則波浪的確定性模擬，目前國內外研究還較少。Naaijen 和Blondel-Couprie[7–8]基于3D FFT 方法對多向不規則海浪在較大區域進行了模擬及預測，但是，海浪的模擬精度隨著時間的增長而降低。劉思[9]將多向不規則波群一個測點的波面信息進行FFT 變換，得到各組成波的頻率、振幅和相位的信息，然后根據多向不規則波的理論模擬方法[10]確定組成波的方向角，再根據線性疊加理論確定多向不規則波群的數值入射邊界條件，對實測波列在數值水池的指定測點處進行了確定性模擬，但其主要致力于波浪要素、波浪群性和方向分布的研究。Draycott 等[11]采用基于時間序列差相位分析（Phase Time Path Difference，PTPD）的方法在圓形水池內重構了多向不規則波浪的方向譜，并對比分析了模擬波列及實驗波列，但其研究主要致力于波浪統計參數如波浪方向譜的驗證。Luo 等[12]通過等分波浪方向分布的方法確定性模擬了多向不規則波浪，但其組成波方向角與特定組成頻率隨機對應，波浪模擬存在一定的誤差。

本文采用線性單疊加模型，建立了多向不規則波浪的確定性模擬方法。通過將模擬的波浪結果與已知波浪過程線進行對比分析，驗證本文建立的多向不規則波浪確定性模擬方法的有效性，并確定了模擬方法的應用條件和適用范圍。

2 波浪確定性模擬方法的建立

采用單疊加方法對多向不規則波浪進行確定性模擬，可將波浪的波面η(x,y,t)表示為

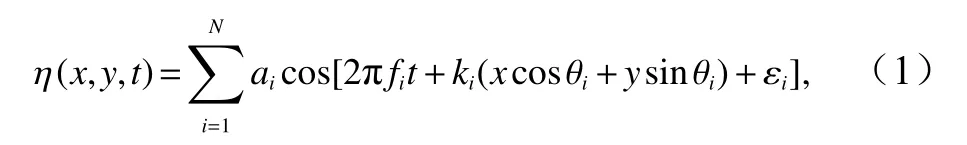
式中，N為組成波個數；ai、fi和θi分別為組成波的振幅、頻率及傳播方向角；ki為組成波的波數；εi為組成波的初始相位，在[0, 2π]內均勻的隨機分布。進行波浪確定性模擬時，N取2n?1，2n為對采集波浪進行FFT 時的數據采樣長度。

公式(1)中，ai、θi及εi需要基于給定的波浪序列來確定。需要說明，為了按下述方法確定波浪的傳播方向，需要3 個以上合適位置的同步時間序列。本文的浪高儀布置形式如圖1 所示。

ai和εi的求解及選取參考Luo 等[12]的處理方法。ai取基于所有測點處的時間序列按單向波求得的組成波幅值aim的平均值，即：

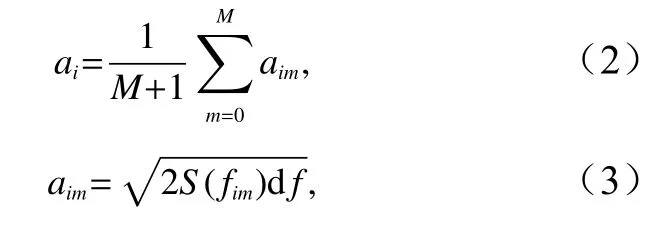
式中，M+1 為陣列浪高儀的總個數；S(fim)為通過FFT分析方法[3]求解的第m個浪高儀處第i個組成波的譜密度值。初始相位εi近似取為圖1 所示的O 點浪高儀通過FFT 變換后直接求解的波浪初相位。

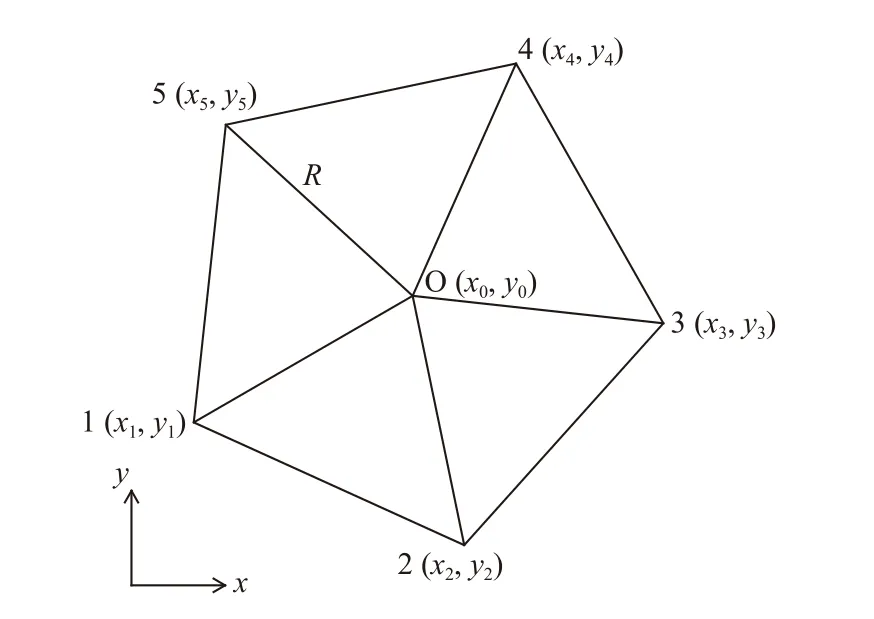
圖1 波浪浪高儀的布置形式Fig. 1 Sketch of the wave gauges

組成波方向角θi的求解采用Borgman[13]和Esteva[14]提出的PTPD 方法，即對3 個非共線的浪高儀同步測得的波浪過程線進行分析，求解組成波的傳播方向角。其求解步驟如下：

（1）在M+1 個浪高儀中，根據的組合個數，確定三角形浪高儀對的組合總個數(本文取M=5)。

（2）對于組成波頻率為fi的組成波，選取有效的三角形浪高儀對組合，即確保每個浪高儀對的任意兩個浪高儀間距L12、L13和L23大于0.01Li且小于等于0.5Li[15–16]，其中，Li為頻率fi基于波浪色散方程所計算的波長。

（3）對所有有效的三角形浪高儀對組合，通過互譜分析，計算相對相位Ф12(fi)和Ф13(fi)。

（4）確定每個有效的浪高儀對對應頻率為fi的組成波的波浪傳播方向角，即

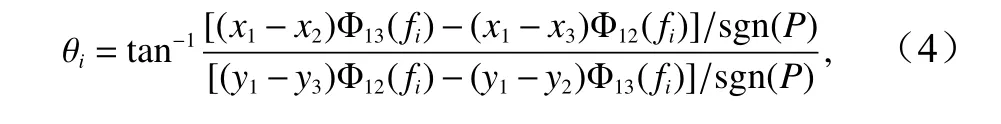
式中，sgn(*)為符號函數；P的計算公式為

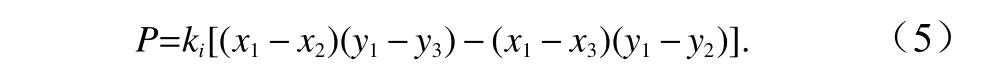
（5）最終，確定對應頻率為fi的組成波的波浪傳播方向θi。可以采用以下兩種方法：在所有有效的浪高儀對中，對不同浪高儀組合所計算的方向角進行平均所得的θi（以下記為average-θi）；在所有有效的浪高儀對中，選取對應波浪能量最大的儀器對所計算的方向角θi（以下記為max-Energy-θi）。

3 確定性波列模擬結果分析

3.1 規則波確定性模擬

不規則波及多向波均是由單向規則波疊加得到的，因此單向規則波精確地確定性模擬是不規則波及多向波浪模擬的基礎。作為示例，取水深h=0.5m，規則波傳播方向θ=π/6，波高H0=0.04m，周期T0=250/256 s=0.977 s (f0=1/T0=1.024 Hz)，為了使得FFT 分析能夠準確地分辨規則波浪的頻率，取T0/Δt為整數，波浪采樣間隔Δt=0.00977 s。計算波浪方向角的浪高儀布置見圖1，其外接半徑R/L=0.224 (R/L=C代表浪高儀間距為C倍的波長)，2n=4096。通過FFT 變換，可以求得：f0=1.024 Hz，H0=2×0.01994m，ε0=?0.012578 rad，average-θi和max-Energy-θi計算的波浪傳播方向角分別為：θ=π×30.173/180 rad 和θ=π×30.215/180 rad。可以看出，通過本文方法計算得到的波浪參數與初始給定的波浪參數基本一致。將模擬的波浪過程線按照求出的H0、ε0、θ計算波高，即

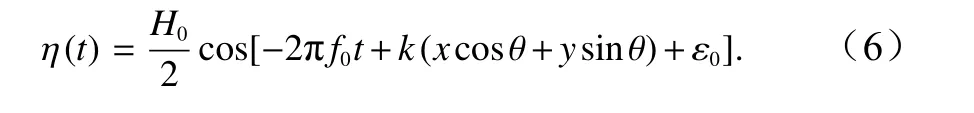
式中，k表示波浪的波數。

作為示例，圖2 給出了確定性模擬的波浪過程線(θ=π×30.173/180 rad)和已知理論計算波浪過程線在t=0～10 s 時于2 號和5 號浪高儀位置的對比。可以看出，模擬的波浪過程線和已知波浪過程線幾乎完全重合。

圖2 2 號（a）和5 號（b）浪高儀在T0=250/256 s，H0=0.04m，θ=π/6 時的波浪過程線Fig. 2 Comparison of the wave surface elevation histories for T0= 250/256 s, H0=0.04m, θ=π/6 of No.2 (a) and No.5 (b) gauges

3.2 理論單向不規則波浪的確定性模擬

進一步，以Ts=1.5 s，Hs=0.04m，θ=0°的理論單向不規則波浪為例，驗證本文方法對單向不規則波浪確定性模擬的有效性。波浪模擬時的頻譜采用Goda 改進的JONSWAP 譜(譜峰升高因子取為3.3)[17]。圖3給出了理論波浪頻譜在fi∈(0，4fp)(fp表示波浪的譜峰頻率)的分布。波浪模擬時，采用時間間隔Δt=0.01 s，采樣長度2n=8192。圖4給出了R/Ls=0.06 和0.12 時，基于average-θi和max-Energy-θi的組成波方向角誤差θEr沿fi的分布情況（Ls表示有效波波長）。θEr的定義如下：

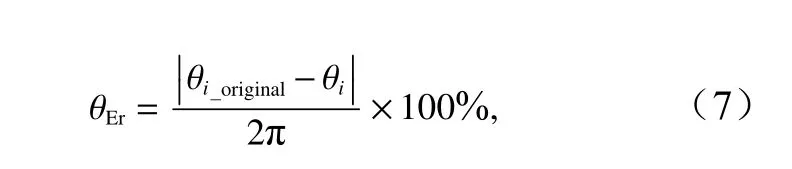
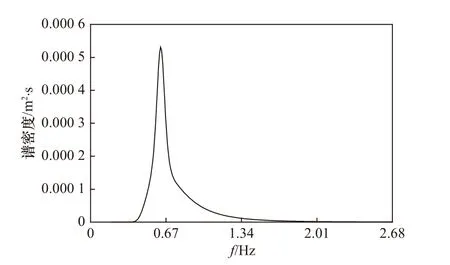
圖3 理論波浪頻譜(Ts=1.5 s，Hs=0.04m)Fig. 3 Theoretical wave frequency spectrum (Ts=1.5 s，Hs=0.04m)

圖4 R/Ls 為0.06 和0.12 時，average-θi 和max-Energy-θi 的θEr 沿fi 的分布（Ts=1.5 s, Hs=0.04m）Fig. 4 Variation of the θEr for average-θi andmax-Energy-θi with fi for R/Ls=0.06 and R/Ls=0.12 (Ts=1.5 s, Hs=0.04m)

式中，θi_original和θi分別為已知的和計算的組成波方向角。通過圖4 可以看出，R/Ls=0.06 和0.12 時的θEr分別在fi>3.2fp和fi>2.3fp時突然增大，這說明計算波浪方向角的fi超出上述范圍后，計算的組成波方向角與理論組成波方向角不一致。這種現象產生的主要原因是由于計算θi的浪高儀間距R大于頻率fi對應波長的0.5 倍所導致的，這與Fernandes 等[15–16]的結論是一致的。此外，通過對比average-θi和max-Energyθi的θEr沿fi的分布可以發現，整體而言，采用averageθi計算的組成波方向角的精度相對較高，θEr相對較小。

進一步，以average-θi在R/Ls=0.06 時計算的組成波傳播方向模擬計算的波浪序列為例，圖5 給出了t=20～40 s，波浪模擬空間范圍的rr/Ls=0.12、0.20、0.35 時，已知波列和重現波列在5 號浪高儀位置的對比（rr代表指定位置與O 點的空間距離）。可以看出，確定性模擬的波列和原始波列幾乎完全重合，僅有微小的振幅高度差及相位偏差，且隨著rr/Ls的增大，波浪的模擬誤差略有增大。

為了定量評估本文提出的波浪確定性模擬方法，定義誤差系數Er為

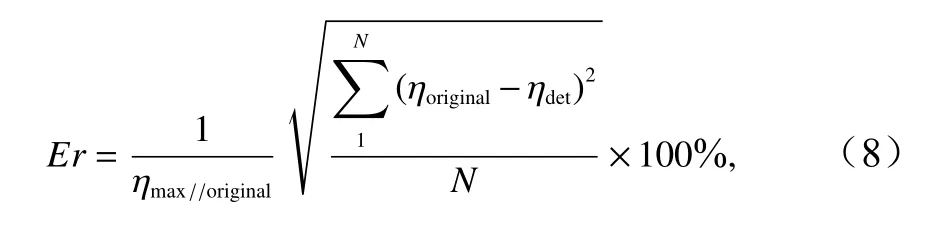
式中，ηoriginal為已知波浪的過程線；ηdet為模擬所得波浪的過程線；ηmax//original為已知波列的最大幅值。以R/Ls為0.06 和0.12 時確定的θi進行波浪模擬的結果為例，圖6a 和圖6b 分別給出了基于average-θi和max-Energy-θi進行波浪模擬時的誤差Ermax隨rr/Ls的變化，其中Ermax為rr/Ls確定后，1～5 號浪高儀位置的波浪確定性模擬的最大誤差。可以看出，Ermax隨著rr/Ls的增大而增大。當R/Ls=0.06 時，基于average-θi和max-Energy-θi的波浪確定性模擬誤差基本一致，但當R/Ls=0.12 時，采用average-θi進行波浪模擬時的誤差明顯比采用max-Energy-θi時的小。此外，結合圖3 及圖4 進行分析，可以看出，fi∈(0，3fp～4fp)時各fi對應的θEr大小是影響波浪確定性模擬精度的重要因素。

3.3 理論多向不規則波浪的確定性模擬

理論多向不規則波浪的模擬基于孫忠濱等[18]采用的頻率?方向對應模型。波浪模擬的頻譜同樣采用Goda[17]改進的JONSWAP 譜(譜峰升高因子取為3.3)。波浪方向分布采用Mstuyasu 型方向分布函數[17]，即

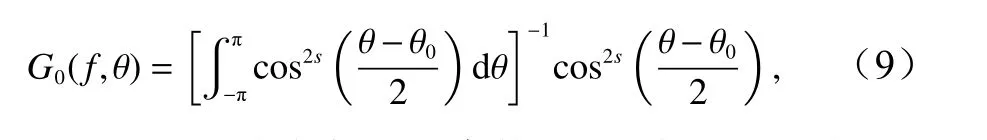
式中，s為方向分布集中度參數；θ0為波浪的主波向。

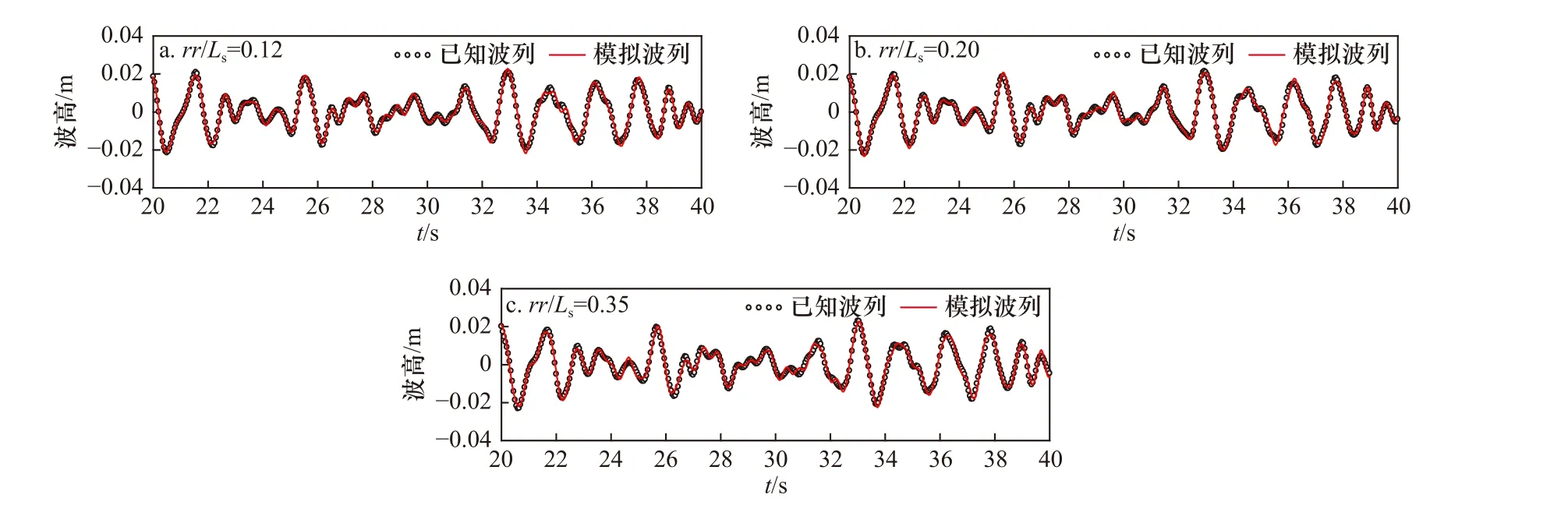
圖5 單向不規則波已知波列和模擬波列在不同rr/Ls 時的對比（Ts=1.5 s，Hs=0.04m）Fig. 5 Comparison of the original and simulated uni-directional irregular wave surface elevation histories (Ts=1.5 s，Hs=0.04m)

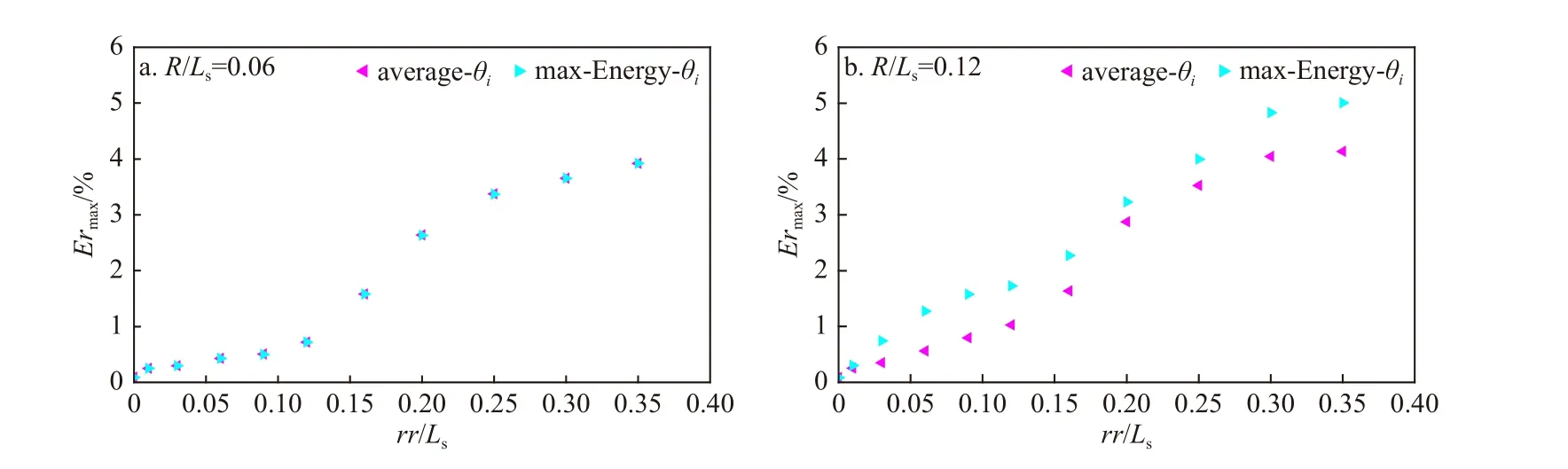
圖6 采用average-θi 和max-Energy-θi 模擬所得波浪的Ermax 隨rr/Ls 的變化（Ts=1.5 s，Hs=0.04m）Fig. 6 Variation of Ermax for simulated waves with rr/Ls using average-θi andmax-Energy-θi respectively (Ts=1.5 s, Hs=0.04m)

理論多向不規則波的波浪參數為：Ts=1.5 s，Hs=0.04m，θ0=0°，s=25。波浪模擬的采樣時間間隔Δt=0.01 s，模擬的序列長度2n=16384。

與單向不規則波浪的研究類似，圖7 以averageθi計算的θEr為例，給出了R/Ls不同時θEr沿fi∈(0，4fp)范圍內的分布。明顯地，θEr沿fi的誤差分布范圍隨著R/Ls的增大而增大，且θEr主要表現在高頻部分。這說明，R/Ls越小，計算的組成波方向角θi在低頻部分的誤差越小。

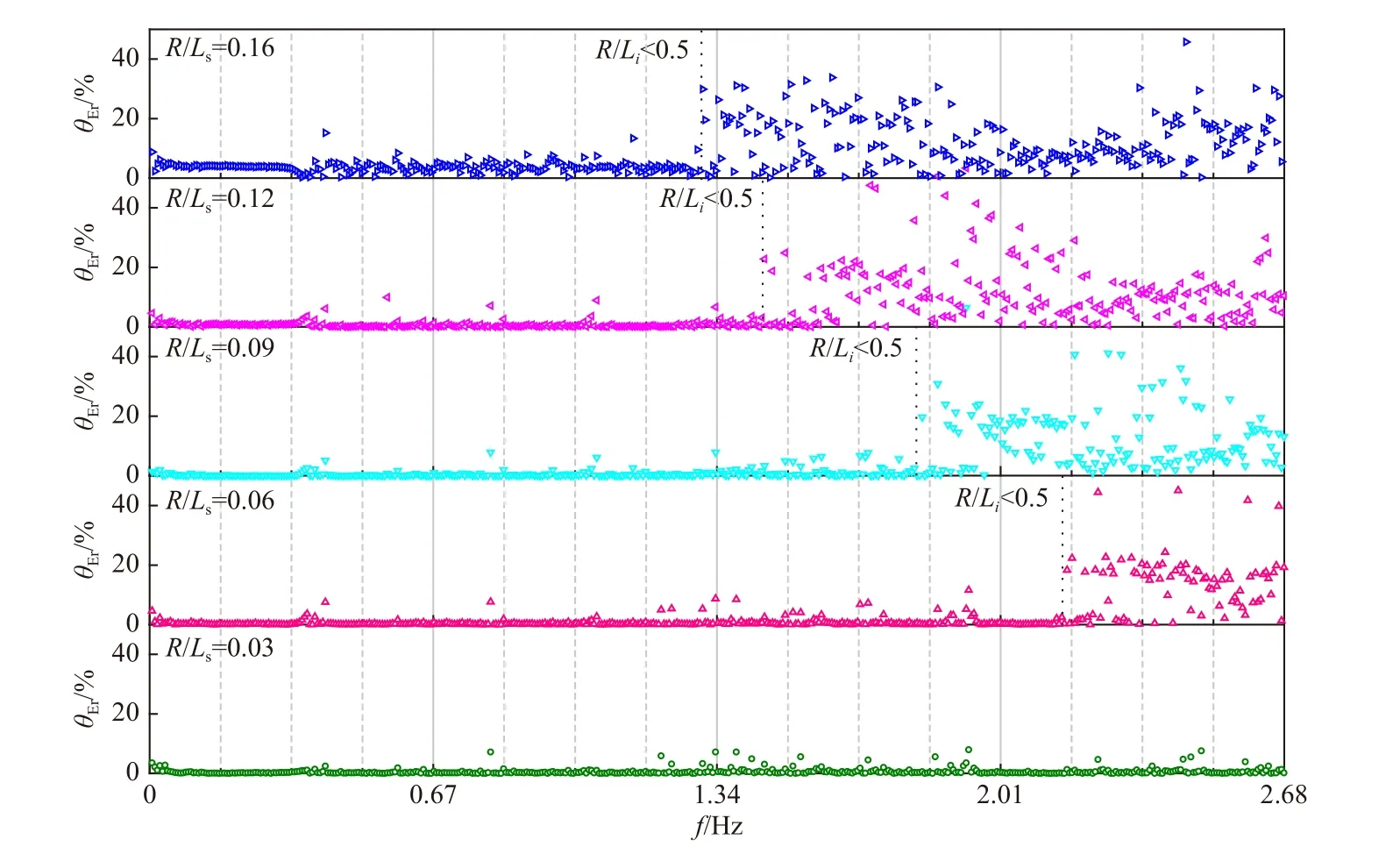
圖7 R/Ls 不同時，采用average-θi 方法計算的θEr 沿fi 的分布（Ts=1.5 s，Hs=0.04m，s=25）Fig. 7 Variation of θEr with fi for average-θimethod with different R/Ls (Ts=1.5 s, Hs=0.04m, s=25)

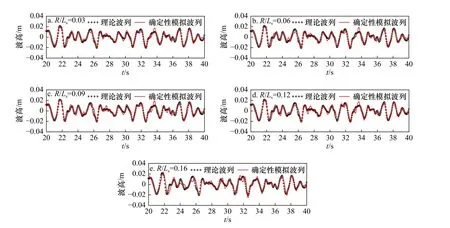
圖8 rr/Ls=0.35，R/Ls 不同時，3 號浪高儀位置理論波列和確定性模擬波列的對比（Ts=1.5 s，Hs=0.04m，s=25)Fig. 8 Comparison of theoretical and simulated wave surface elevation histories for different R/Ls with rr/Ls=0.35 at No.3 gauge (Ts=1.5 s,Hs=0.04m, s=25)

為了進一步驗證R/Ls的變化對多向不規則波浪確定性模擬的影響，圖8 以采用average-θi所得波浪模擬結果為例，給出了rr/Ls=0.35，不同R/Ls時，3 號浪高儀位置的理論波列和模擬波列的對比。可以看出，當R/Ls≤0.12 時，模擬波列和理論波列的波動過程是基本一致的，但當R/Ls=0.16 時，兩者的差別相對較大。結合圖7 的θEr在fi∈(0，4fp)范圍內的分析結果可認為，模擬波列同理論波列差別產生的原因是由于當R/Ls=0.12，fi<2.3fp時，絕大多數組成波方向角誤差θEr<2%，僅有個別的組成波方向角誤差θEr稍大，但也小于10%，保證了絕大多數的波浪能量對應的計算的組成波的傳播方向θi是準確的，從而保證了波浪模擬的整體精度。明顯地，當R/Ls=0.16 時，在fi<1.95fp內的θEr大于R/Ls>0.12 時的θEr，且絕大多數θEr≈5%；此外，波浪高頻成分組成波的θEr也會導致重現波浪在高頻部分產生較大的模擬誤差，從而導致模擬波列和已知波列整體差別較大。

為了研究多向不規則波確定性模擬的有效范圍，圖9 以R/Ls=0.06，選取average-θi進行的波浪確定性模擬結果為例，給出了3 號浪高儀位置處理論波列和模擬波列在t=20～40 s，rr/Ls=0.16、0.35、0.60 和0.80時的對比。可以看出，隨著波浪模擬空間范圍的增大，確定性模擬的波浪精度減小，模擬的波列與理論波浪過程線在時域上存在的振幅差及相位偏差隨著rr/Ls的增大而逐漸增大。當rr/Ls=0.80，即確定性模擬的波浪范圍為1.6Ls時，波浪確定性模擬的誤差相對較大，但模擬波列和理論波列仍然具有一致性。

與單向不規則波浪的波浪模擬精度分析類似，圖10以R/Ls=0.06 為例，給出了多向不規則波采用averageθi和max-Energy-θi進 行 波 浪 模 擬 時 分 析 的Ermax隨rr/Ls的變化。明顯地，當rr/Ls確定后，采用averageθi方法計算的組成波方向角進行波浪確定性模擬時的Ermax較采用max-Energy-θi方法計算的組成波方向角進行波浪模擬時的Ermax小。這與單向不規則波浪所得的結論是一致的。

圖10 R/Ls=0.06 時采用計算的average-θi 和max-Energy-θi 模擬所得波浪的Ermax 隨rr/Ls 的變化（Ts=1.5 s,Hs=0.04m, s=25）Fig. 10 Variation of Ermax for simulated waves with rr/Ls using average-θi andmax-Energy-θi of R/Ls=0.06 (Ts=1.5 s,Hs=0.04m, s=25)

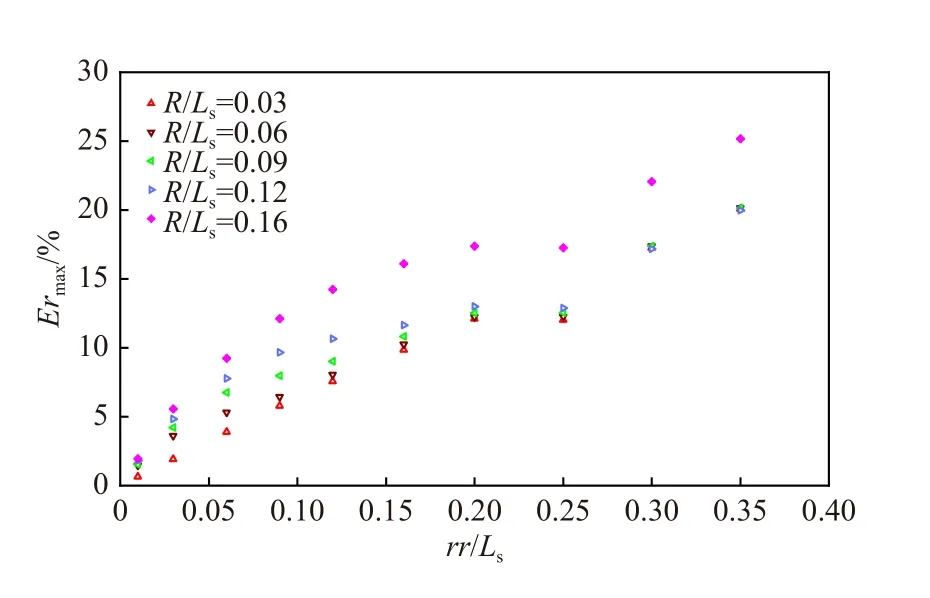
圖11 不同的R/Ls 采用average-θi 模擬所得波浪的Ermax 隨rr/Ls 的變化(Ts=1.5 s, Hs=0.04m, s=25)Fig. 11 Variation of Ermax for simulated waves with rr/Ls using average-θi with different R/Ls (Ts=1.5 s, Hs=0.04m, s=25)

圖11 以采用average-θi計算的組成波方向角進行確定性模擬的多向不規則波為例，給出了R/Ls不同時，波浪模擬的Ermax隨空間范圍rr/Ls的變化情況。隨著rr/Ls的增大，波浪模擬的Ermax增大；當rr/Ls相同時，Ermax隨著R/Ls的增大而增大。明顯地，rr/Ls一定時，R/Ls=0.16 時的Ermax與R/Ls=0.12 時的Ermax絕對差值|Ermax_0.16?Ermax_0.12|明顯地比|Ermax_0.12?Ermax_0.09|、|Ermax_0.09?Ermax_0.06|及|Ermax_0.06?Ermax_0.03|時 的 大；且R/Ls=0.03～0.12時，確定性模擬波浪的Ermax的差別不是很大。因此，為了保證采用本文方法進行波浪確定性模擬的準確性，采集波浪的浪高儀間距應小于波浪有效波長的0.12 倍。另外，綜合圖11 和圖9b 的結果可以看出，當R/Ls≤0.12 時，在空間范圍rr/Ls<0.35 內，即確定性模擬的波浪范圍小于0.7Ls時，模擬的波列與原始波列的差別較小，即Ermax≤20%，一般滿足波浪對結構物作用的試驗要求。

4 結論

基于單疊加模型，通過對給定的合適位置的多向不規則波浪同步波動過程求解，確定各組成的波浪成分ai、ωi、θi及εi，并以單疊加數值計算模型，實現了多向不規則波的確定性模擬。通過定性對比分析模擬波列和已知波列在時域的分布情況及定量分析模擬波列的誤差分布情況，可得出如下結論：

（1）本文建立的方法可以在一定范圍內確定性的模擬給定的多向不規則波波動過程。但是，波浪的相位差和振幅高度差隨著波浪模擬范圍的增大而增大，即波浪重現誤差隨著波浪重現范圍的增大而增大。

（2）采用對不同浪高儀組合所計算的方向角進行平均所得的average-θi為組成波方向角進行波浪確定性模擬的結果優于采用對應波浪能量最大儀器對所計算的方向角max-Energy-θi為組成波方向角時的模擬結果。

（3）給定計算組成波傳播方向θi的各浪高儀間距應小于波浪有效波長的0.12 倍。

（4）當R/Ls≤0.12 時，在空間范圍rr/Ls<0.35 內，即確定性模擬的波浪范圍小于0.7Ls時，模擬的波浪與原始波浪的差別較小，即Ermax≤20%，一般滿足波浪對于結構物作用的試驗要求。